算法——排序
排序
下面的代码会用到宏定义,因为再C中没有swap交换函数,所以对于swap的宏定义代码如下:
#define swap(a, b) {\__typeof(a) __a = a; a = b; b = __a;\ }
稳定排序:
1.插入排序:
插入排序会将数组,分位两个部分,一般分为前后两部分,而前半部分为已排序区,后半部分为未排序区;插入排序的操作就是把,未排序区中的元素插入到已排序区中的去,并且满足排序区的单调性;如图下面的操作,实现一个单调递增序列:
数组的原本样子,现在使位置0是已排序区,先去从位置1开始去插入;
将12插入到23前面,使位置0,1形成单调递增;
进行插入,对位置2插入,发现不用插入,直接对下一个位置进行插入:
位置4也不用进行插入保持原位置,对位置5进行插入:
最后完成排序;
时间复杂度:
代码实现:
void insert_sort(int *arr, int n) {//arr排序数组,n数组长度for (int i = 1; i < n; i++) {//位置0开始定为已排序区for (int j = i; j >= 1 && arr[j] < arr[j - 1]; j--) {//将位置i进行插入到前面的以排序区swap(arr[j], arr[j - 1]);//交换位置}}return ; }2.冒泡排序:
冒泡排序,为什么会叫冒泡排序,假如实现单调递增序列,那么每一次都会将未排序中的最大的元素放到未排序区中的最后去,把数组立起来数组的最后的位置在上,那么是不是每次未排序的最大元素会像冒泡一样往上升,所以叫冒泡排序;
如图数组最开始状态:
第一次冒泡:
第一次完冒泡后,最大的元素已经放到了数组最后位置,也相当于放到了已排序区中了;然后这样一直循环直到排完序;
时间复杂度:
代码实现:
做了一个小小的优化;
void bubble_sort(int *arr, int n) {int time = 1;//用来标记这次循环是否发生了冒泡交换for (int i = 1; i < n && time; i++) {//如果没有发生交换说明数组已经排好了序time = 0;for (int j = 0; j < n - i; j++) {if (arr[j] >= arr[j + 1]) {swap(arr[j], arr[j + 1]);time++;}}}return ; }3.归并排序:
将一个数组从中间分开,然后通过递归一直将子数组进行分开,直到数组只有两个元素,然后通过回溯的过程中进行排序,然后一直回溯到整个数组并拢,完成排序;
如图,将数组这样二分下去:
然后从下往上进行排序,单调递增:
合并,排序:
合并,在排序:
最终完成排序;
时间复杂度:
代码实现:
这个过程比较容易理解,就是代码实现有那么一点复杂,来看代码:
void merge_sort(int *arr, int l, int r) {//数组的头位置,r数组的末尾在if (r - l <= 1) {//当分到只有2个元素和1个元素时,递归出口if (r - l == 1 && arr[l] > arr[r]) {//两个元素,进行排序swap(arr[l], arr[r]);}return ;}int mid = (l + r) >> 1;//开始分列merge_sort(arr, l, mid);//递归左边数组merge_sort(arr, mid + 1, r);//递归右边数组int *temp = (int *)malloc(sizeof(int) * (r - l + 1));//创建一个空间,来存子数组的元素int p1 = l, p2 = mid + 1, k = 0;//p1数组分裂开的前部分的起始坐标,p2数组分裂开后半部分的起始坐标while (p1 <= mid || p2 <= r) {if (p2 > r || (p1 <= mid && arr[p1] < arr[p2])) temp[k++] = arr[p1++];else temp[k++] = arr[p2++];}memcpy(arr + l, temp, sizeof(int) * (r - l + 1));//将排好序的子数组拷贝给原数组free(temp);return ; }4.基数排序:
这里假设数组都是两位数,先对数组进行元素的个位进行排序,然后在对数组的十位进行排序,这样就能对数组拍好序;如果位数不相同,取位数最大的数进行位数排序假如最大的位数是3位,那么就进行3次位数排序,如果位数10位那就进行10次位数排序;
如图数组最初:
进行个位排序,上面的表格就是对于个位数的统计,对于排序时会起到作用:

在进行10位排序:
最终完成排序:
时间复杂度:
代码实现:
void number_sort(int *arr, int n, int exp) {int count[10] = {0};for (int i = 0; i < n; i++) {count[arr[i] / exp % 10] += 1;//对每位数的数的个数统计}for (int i = 1; i < 10; i++) {count[i] += count[i - 1];//位数排序,从小到大,现在的操作就是使count变为下标}int *sum = (int *)malloc(sizeof(int) * n);for (int i = n - 1; i >= 0; i--) {//假如个位已近排序后,那么个位大的在后,而根据十位排序也是从高位排到低位,所以需要倒过来存sum[count[arr[i] / exp % 10] - 1] = arr[i];//下标从0开始,所以需要-1;count[arr[i] / exp % 10]--;//对应的位数已经排序一个,所以数量-1;}memcpy(arr, sum, sizeof(int) * n);free(sum);return ; }void radix_sort(int *arr, int n) {int max = INT_MIN;for (int i = 0; i < n; i++) {//获取最大数的数max = max > arr[i] ? max : arr[i];}for (int i = 1; max / i > 0; i *= 10) {//从个位一直到大于最大数的位数number_sort(arr, n, i);}return ; }非稳定排序:
1.选择排序:
将数组分为两个区域一个已排序区和一个未排序区,每次将未排序区中的最值放在已排序区中;
如图将54放放到最后,也就是已排序区中;
这样一直在未排序区中选择,直到排序完成:
时间复杂度:
代码实现:
void select_sort(int *arr, int n) {//这里实现的是将最小的元素放在最前面,现在前面就是已排序区for (int i = 0; i < n - 1; i++) {int ind = i;//ind先记录当前准备排序的位置for (int j = i + 1; j < n; j++) {if (arr[ind] > arr[j]) ind = j;//ind记录未排序区中最小值的值的位置}swap(arr[ind], arr[i]);//将未排序的区的最小值放在准备排序的位置}return ; }2.快速排序:
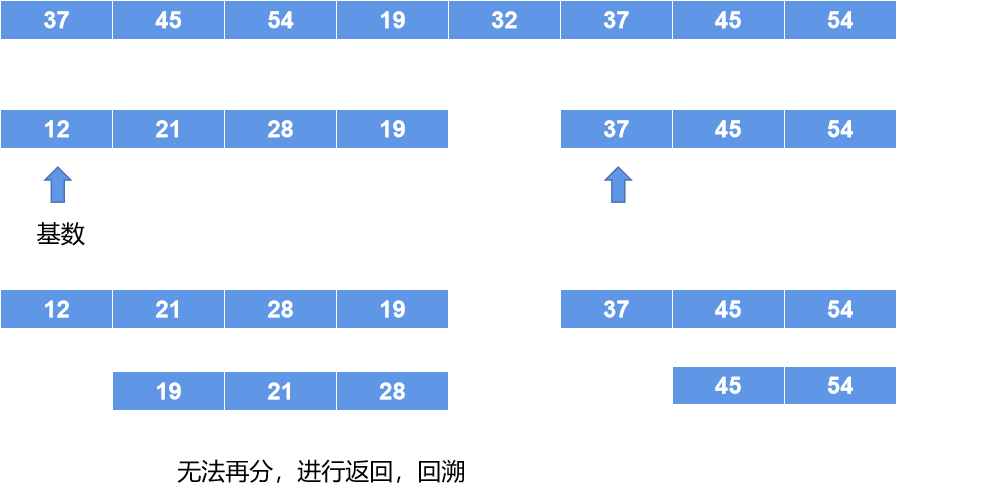
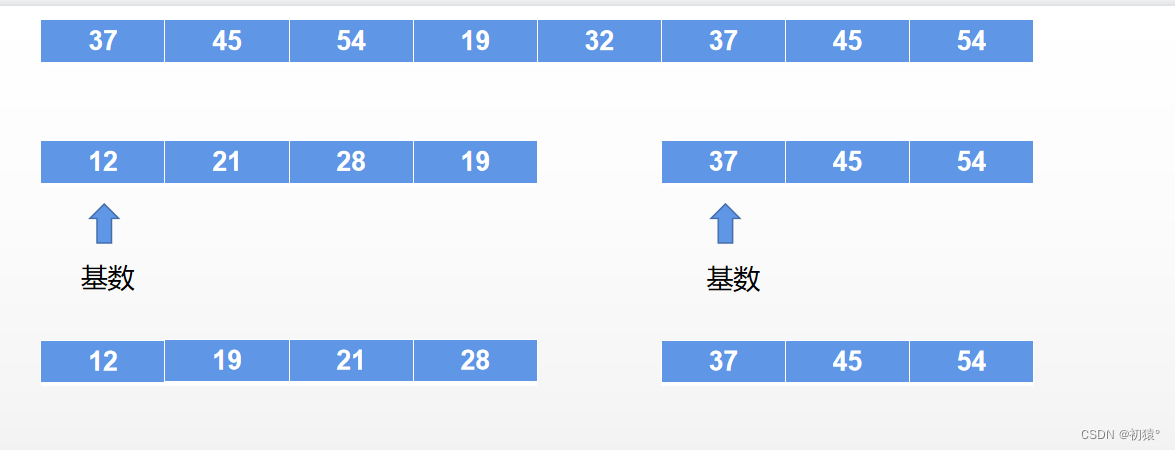
选择数组头步位置,作为基数,用一个变量记录下来,然后将这个基数作为中间值,将数组分为两个部分,前半部分小于这个基数,后半部分大于基数,然后在对两个部分进行上面的操作,直接这两个部分不能再分;这里不一定是二分开的,有可能这个基数是最大值,那么就没有前半部分;
如图数组初始状态:
将32作为基数,把数组分为两部分分:
然后再对左边部分进行快排,右边部分进行快排
这里只是刚好,不用变化,然后继续上面的操作,直到最后排完序:
完成排序。
时间复杂度:
最坏:
代码实现:
//l最初为0,r最初为n-1 void quick_sort(int *arr, int l, int r) {if (r < l) return ;int x = l, y = r, num = arr[l];while (x < y) {while (x < y && arr[y] >= num) y--;//如果大于基数的部分,该位置数大于基数就不用交换if (x < y) arr[x++] = arr[y];//如果x<y,说明y位置的值是小于基数的,就放到前面去,第一次的时候x的位置就是基数的位置,所以覆盖的是基数的位置while (x < y && arr[x] <= num) x++;//如果小于基数的部分,该位置数小于等于基数就不用交换if (x < y) arr[y--] = arr[x];//x<y,说明x位置的值是小于基数的,现在y位置是之前小于基数的位置,直接覆盖}arr[x] = num;//将基数放到分割位置quick_sort(arr, l, x - 1);//小于基数的部分quick_sort(arr, x + 1, r);//大于基数的部分return ; }3.希尔排序
希尔排序其实就是对于选择排序的一个优化的算法,而最最坏的情况就是降为一个普通的选择排序。
选择一个移动的长度,最开始选择数组长度的1/2,然后一直除2,直到步长等于1,进行一次插入排序;这个步长的作用就是,从一个位置往前移动多少步进行对该位置的值进行比较,如果不满住单调性就进行交换,然后交换如果还能往前目前的步长长度,继续往前比较;
如图,直接上图片理解:
现在的步长选作4,那么就从位置4进行开始排序:
他俩进行比较,然后数组是单调递增,就就需要交换,然后比较位置向后移动:
然后第一次步长结束后,那么步长在除以2:
然后再次进行比较
继续往后
这里发生了交换,而且现在的位置还能往前走步长,所以也需要比较:
比较后,不用发生交换,继续刚刚的位置往后:
这里发生了交换,又需要往前走:
直到不能发生交换,然后现在走到了最后的位置,进行步数除以2,等于1,进行一次选择排序:
这里发生了交换,那就需要再往前走步长那么长进行比较:
最后遍历,没有发生交换,并且步长为除2等于0了,完成排序;
时间复杂度:
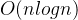
最坏:
代码实现:
void shell_sort(int *arr, int n) {int step;for (step = n / 2; step > 0; step >>= 1) {//步长循环for (int i = step; i < n; i++) {//从步长长度开始往后循环for (int j = i; j >= step && arr[j] < arr[j - step]; j -= step) {//如果不满足单调性,发生交换,并且如果现在的位置长度大于等于步长继续往前移动进行比较swap(arr[j], arr[j - step]);}}}return ; }4.堆排序:
堆,堆排序在前面这个链接的文章里,因为单独将堆排序有那么一点难理解需要结合对堆的理解才容易一些;
相关文章:
算法——排序
排序 下面的代码会用到宏定义,因为再C中没有swap交换函数,所以对于swap的宏定义代码如下: #define swap(a, b) {\__typeof(a) __a a; a b; b __a;\ } 稳定排序: 1.插入排序: 插入排序会将数组,分位两个部…...
leetCode动态规划“不同路径II”
迷宫问题是比较经典的算法问题,一般可以用动态规划、回溯等方法进行解题,这道题目是我昨晚不同路径这道题趁热打铁继续做的,思路与原题差不多,只是有需要注意细节的地方,那么话不多说,直接上coding和解析&a…...

100天精通Python(可视化篇)——第99天:Pyecharts绘制多种炫酷K线图参数说明+代码实战
文章目录 专栏导读一、K线图介绍1. 说明2. 应用场景 二、配置说明三、K线图实战1. 普通k线图2. 添加辅助线3. k线图鼠标缩放4. 添加数据缩放滑块5. K线周期图表 书籍推荐 专栏导读 🔥🔥本文已收录于《100天精通Python从入门到就业》:本专栏专…...

哈希表与有序表
哈希表与有序表 Set结构 key Map结构 key-value 哈希表 哈希表的时间复杂度都是常数项级别的,但常数较大 增删改查的时间都是常数级别的,与数据量无关 当哈希表存储的值是基础数据类型(Integer - int),哈希表中内…...

什么时候使用RPA?如何使用RPA?需要什么样的硬件支持?需要安装哪些软件?
RPA(Robotic Process Automation)是一种用于自动化执行重复性任务的技术,它可以帮助企业提高工作效率,降低人力成本,并减少人为错误。RPA适用于各种行业和场景,例如财务、人力资源、客户服务、IT运维等。 …...
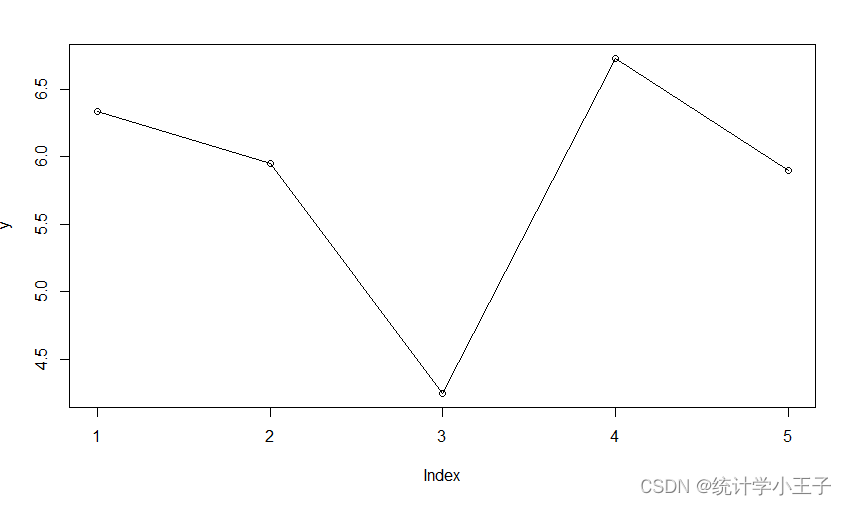
R语言入门——line和lines的区别
目录 0 引言一、 line()二、 lines() 0 引言 首先,从直观上看,lines比line多了一个s,但它们还是有很大的区别的,下面将具体解释这个两个函数的区别。 一、 line() 从R语言的帮助文档中找到,line()的使用,…...
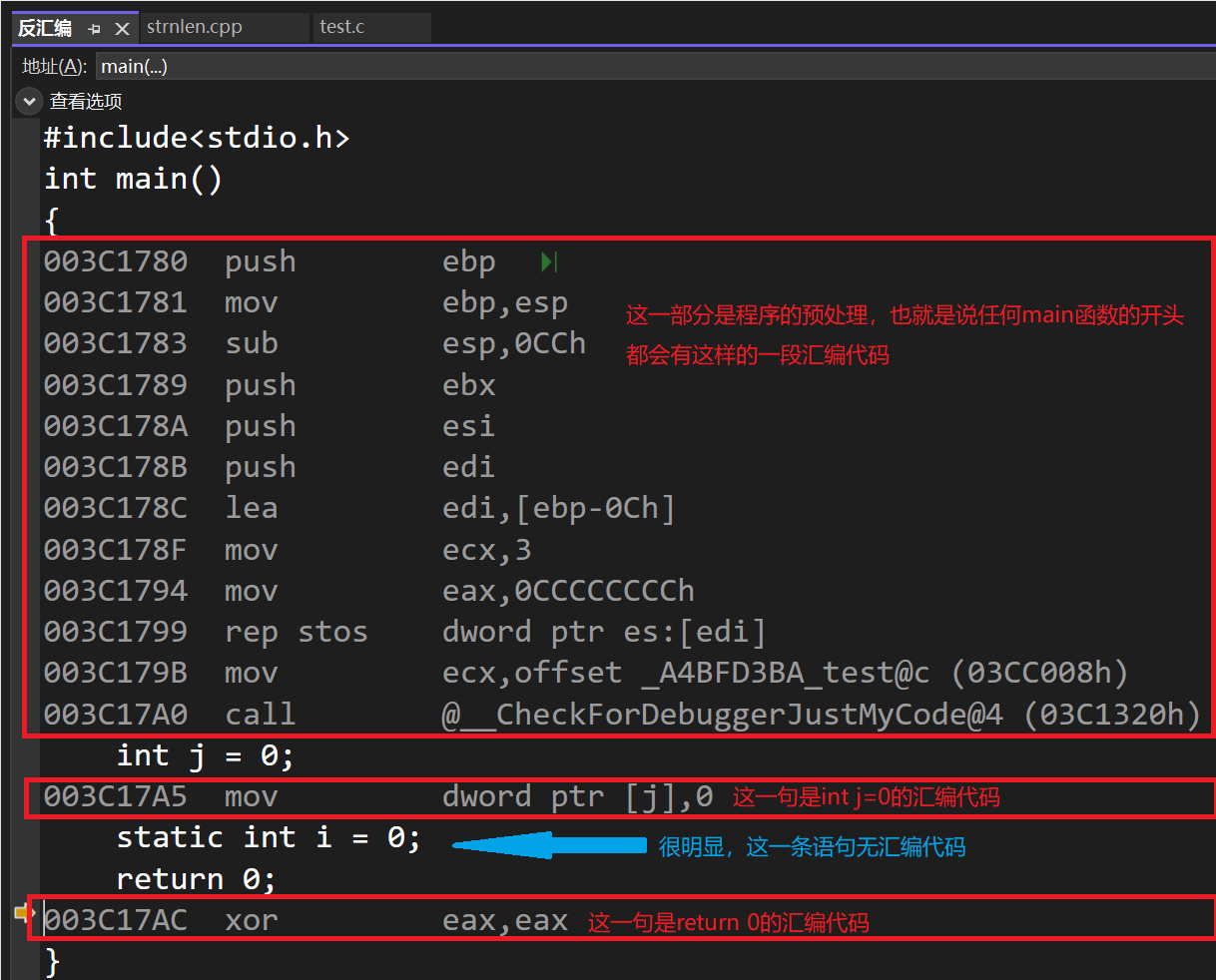
C语言:static关键字的使用
1.static修饰局部变量 这是static关键字使用最多的情况。我们知道局部变量是在程序运行阶段在栈上创建的,但是static修饰的局部变量是在程序编译阶段在代码段(静态区)创建的。所以在static修饰的变量所在函数执行结束后该变量依然存在。 //…...
:ECUM的ISOLAR-AB配置及代码解析)
AUTOSAR知识点 之 ECUM (三):ECUM的ISOLAR-AB配置及代码解析
目录 1、概述 2、ISOLAR-AB配置 2.1、EcuMGeneral 2.2、EcuMConfiguration 2.2.1、EcuMDefaultShutdownTarget 2.2.2、EcuMDriverInitListOne...
2023年MySQL-8.0.34保姆级安装教程
重点放前面:演示环境为windows环境。 MySQL社区版本安装教程如下: 一、MySQL安装包下载二、安装配置设置三、配置环境变量 大体分为3个步骤:①安装包的下载;②安装配置设置;③配置环境变量 一、MySQL安装包下载 下载官…...
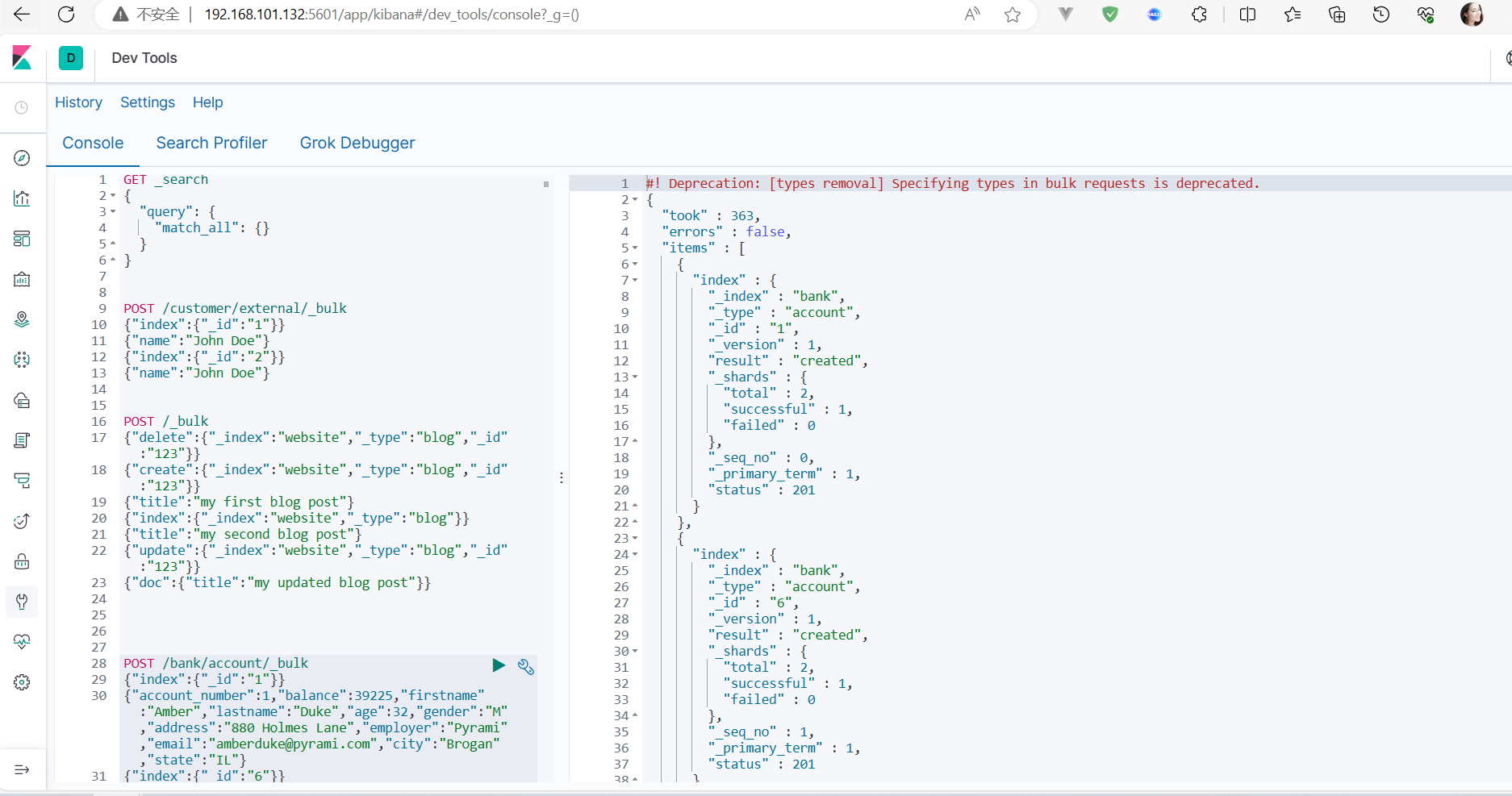
ElasticSearch入门
一、基本命令_cat 1、查看节点信息 http://192.168.101.132:9200/_cat/nodes2、查看健康状况 http://192.168.101.132:9200/_cat/health3、查看主节点的信息 http://192.168.101.132:9200/_cat/master4、查看所有索引 http://192.168.101.132:9200/_cat/indices二、索引一…...

RocketMQ的Broker
1 Broker角色 Broker角色分为ASYNC_MASTER (异步主机)、SYNC_MASTER (同步主机)以及SLAVE (从机)。如果对消息的可靠性要求比较严格,可以采用SYNC_MASTER加SLAV E的部署方式。如果对消息可靠性要求不高,可以采用ASYNC_MASTER加ASL AVE的部署方式。如果只…...

使用Puppeteer进行游戏数据可视化
导语 Puppeteer是一个基于Node.js的库,可以用来控制Chrome或Chromium浏览器,实现网页操作、截图、测试、爬虫等功能。本文将介绍如何使用Puppeteer进行游戏数据的爬取和可视化,以《英雄联盟》为例。 概述 《英雄联盟》是一款由Riot Games开…...

【Flask】from flask_sqlalchemy import SQLAlchemy报错
【可能出现的情况】 1、未安装 Flask-SQLAlchemy: 在使用 flask_sqlalchemy 之前,你需要确保已经通过 pip 安装了 Flask-SQLAlchemy。可以通过以下命令安装它: pip install Flask-SQLAlchemy 2、包名大小写问题: Python 是区分大…...

索引简单概述(SQL)
一、什么是索引? 索引是一种特殊的文件(InnoDB数据表上的索引是表空间的一个组成部分),他们包含着对数据表里所有记录的引用指针。 索引是一种数据结构。数据库索引,是数据库管理系统中一个排序的数据结构࿰…...

union all 和 union 的区别,mysql union全连接查询
602. 好友申请 II :谁有最多的好友(力扣mysql题,难度:中等) RequestAccepted 表: ------------------------- | Column Name | Type | ------------------------- | requester_id | int | | accepter_id | int | | accept_date …...

UDP和TCP的区别
UDP (User Datagram Protocol) 和 TCP (Transmission Control Protocol) 是两种常见的传输层协议。它们在设计和用途上有很大的区别,以下是它们的主要差异: 连接性: TCP: 是一个连接导向的协议。它首先需要建立连接,数据传输完毕后再终止连接…...

阿里云 MSE 助力开迈斯实现业务高增长背后带来的服务挑战
开迈斯新能源科技有限公司于 2019 年 5 月 16 日成立,目前合资股东分别为大众汽车(中国)投资有限公司、中国第一汽车股份有限公司、一汽-大众汽车有限公司[增资扩股将在取得适当监督(包括反垄断)审批后完成]、万帮数字…...

消灭怪物的最大数量【力扣1921】
一、题目分析 需要满足的条件: 只能在每分钟的开始使用武器武器能杀死距离城市最近的怪兽怪兽到达城市就会输掉游戏 游戏最优策略:我们可以在每分钟的开始都使用一次武器,用来杀死距离城市最近的怪兽。这样可以在力所能及的范围内…...

数据结构之算法
算法的基本概念 计算机解题的过程实际上是在实施某种算法,这种算法称为计算机算法 算法的基本要素 一个算法是由两种基本要素组成:一是对数据对象的运算和操作;二是算法的控制结构 算法中对数据的运算和操作 在一般计算机系统中…...

MyBatis与MyBatis-Plus的分页以及转换
一、介绍 MyBatis和MyBatis-Plus都是Java持久化框架,用于简化数据库访问和操作。它们提供了面向对象的方式来管理关系型数据库中的数据。 MyBatis是一个轻量级的持久化框架,通过XML或注解配置,将SQL语句与Java对象进行映射,使开…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...