数学建模--时间序列预测模型的七种经典算法的Python实现
目录
1.开篇版权提示
2.时间序列介绍
3.项目数据处理
4.项目数据划分+可视化
5.时间预测序列经典算法1:朴素法
6.时间预测序列经典算法2: 简单平均法
7.时间预测序列经典算法3:移动平均法
8.时间预测序列经典算法4:简单指数法
9.时间预测序列经典算法5:Holt线性趋势法
10.时间预测序列经典算法6:Holt-Winters季节性预测算法
11.时间预测序列经典算法7:自回归移动平均(ARIMA)算法
12.参考文章和致谢
1.开篇版权提示
"""
开篇提示:
这篇文章的绝大部分代码都不是我自己书写的,而是来自:https://www.cnblogs.com/lfri/articles/12243268.html#gallery-5的文章中。
由于目前很多的时间序列预测模型的文章中都没有给出相关的数据集,所以我不能够很好的进行对应的学习和代码的运行
而这篇文章,给出了对应的数据集,所以我就通过这篇文章来对于时间序列预测模型有一个更好的理解,在这里对于这位作者表示不尽的感谢!
如果有涉及到版权问题,请及时联系我对文章做相应的修改或者删除!
再次申明:
代码文章出处:https://www.cnblogs.com/lfri/articles/12243268.html#gallery-5
本人仅作学习参考使用,本篇博客也仅作相关的理解研究的标注,需要更深的理解交流请跳转上述网址出处,本人不胜感激!
"""2.时间序列介绍
时间序列介绍
"""
时间预测序列模型是一个非常强大的预测模型算法,其体现在对于根据先前的数据经验的整理学习来完成对于未来的合理预测和计算,是数学建模中一种基础的预测算法。
文章将通过一个项目的处理解决来对于7种时间序列预测的模型算法的研究并且对比分析它们的优缺点和不足之处
"""
实践项目题目
"""
Question:
假设给出了过去两年不同时间段的乘客的数量,要求你根据这些数据(2012 年 8 月至 2014 年 8月),需要用这些数据预测接下来 7 个月的乘客数量。
注意:数据集保存在时间预测模型材料包中,详见:time_data.csv
"""3.项目数据处理
"""
首先我们通过pandas对于数据集有一个简单的了解,该数据集是由18288个数据组构成的,其中包括了其ID,Datetime和Count数据
通过df.head(10)我们查阅了前10列的元素,对于数据集有了相应的理解。
"""import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv('C:\\Users\\Zeng Zhong Yan\\Desktop\\时间预测模型材料包\\time_data.csv')
df.head()
df.shape#(18288, 3)print(df.head(10))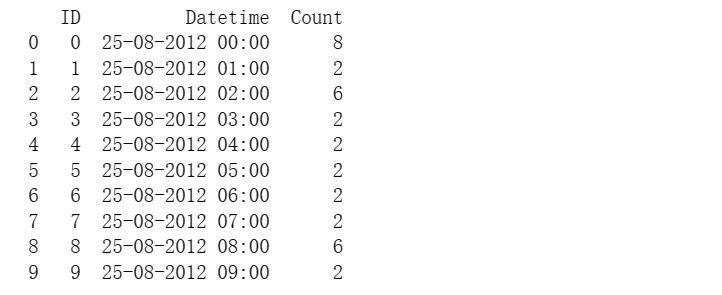
4.项目数据划分+可视化
"""
现在我们需要进行进一步的处理:
我们将前11856个元素,也就是从2012 年8月-2013年12月的数据单独拿出来制作一个数据集,以此作为训练集
我们再将剩余的元素拿出来作为作为测试集,用来检测模型的精确程度。
接下来我们将完成3个步骤:
#1.对于训练数据和测试数据进行步划分
#2.对于数据进行一个采样划分
#3.进行可视化绘图
"""import pandas as pd
import matplotlib.pyplot as pltdf = pd.read_csv('C:\\Users\\Zeng Zhong Yan\\Desktop\\时间预测模型材料包\\time_data.csv', nrows=11856)
#对于训练数据和测试数据进行步划分
train = df[0:10392]
test = df[10392:]#对于数据进行一个采样划分
df['Timestamp'] = pd.to_datetime(df['Datetime'], format='%d-%m-%Y %H:%M') # 4位年用Y,2位年用y
df.index = df['Timestamp']
df = df.resample('D').mean() #按天采样,计算均值train['Timestamp'] = pd.to_datetime(train['Datetime'], format='%d-%m-%Y %H:%M')
train.index = train['Timestamp']
train = train.resample('D').mean() #test['Timestamp'] = pd.to_datetime(test['Datetime'], format='%d-%m-%Y %H:%M')
test.index = test['Timestamp']
test = test.resample('D').mean()#绘制测试集和训练集的点在图片上,进行可视化后知道数据是如何变化的
train.Count.plot( title= 'Daily Ridership', fontsize=14)
test.Count.plot(title= 'Daily Ridership', fontsize=14)
plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/时间序列1.png', dpi=500, bbox_inches='tight')
plt.show()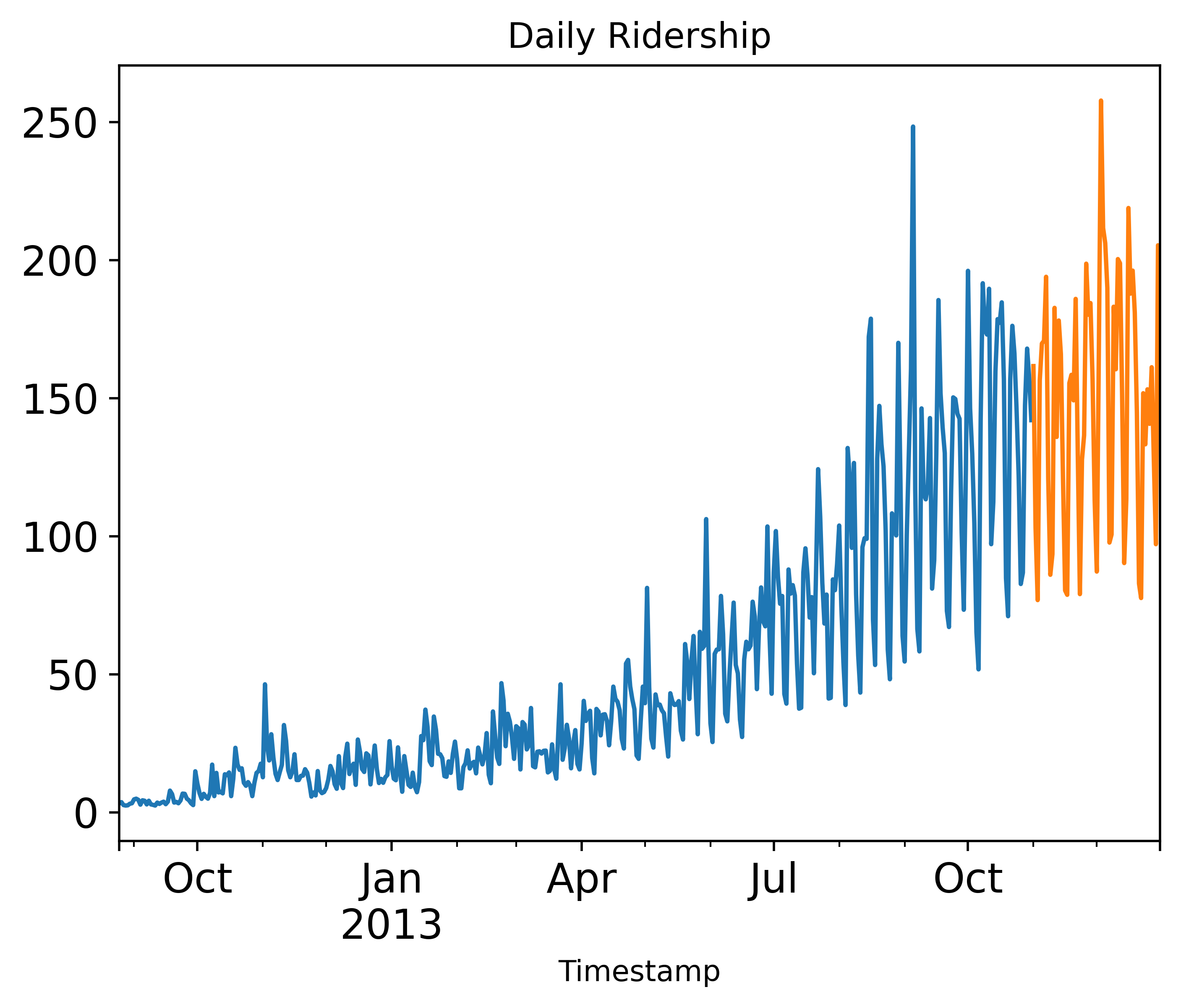
5.时间预测序列经典算法1:朴素法
"""
经典算法1:朴素法
朴素法的思想告诉我们,如果一个对象的变化很平稳,只会进行一般的波动,那么我们就可以预测t+1天的数值y(t+1)=y(t)
所以我们可以设想,朴素法预测之后的图像应该失调平稳的直线。
如下图所示,我们可以明显的发现朴素法的预测明显差距过大了,显然这很不合适。
朴素法并不适合变化很大的数据集,最适合稳定性很高的数据集。
"""dd = np.asarray(train['Count'])
y_hat = test.copy()
y_hat['naive'] = dd[len(dd) - 1]
plt.plot(train.index, train['Count'], label='Train')
plt.plot(test.index, test['Count'], label='Test')
plt.plot(y_hat.index, y_hat['naive'], label='Naive Forecast')
plt.legend(loc='best')
plt.title("Naive Forecast")
plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/时间序列2.png', dpi=500, bbox_inches='tight')
plt.show()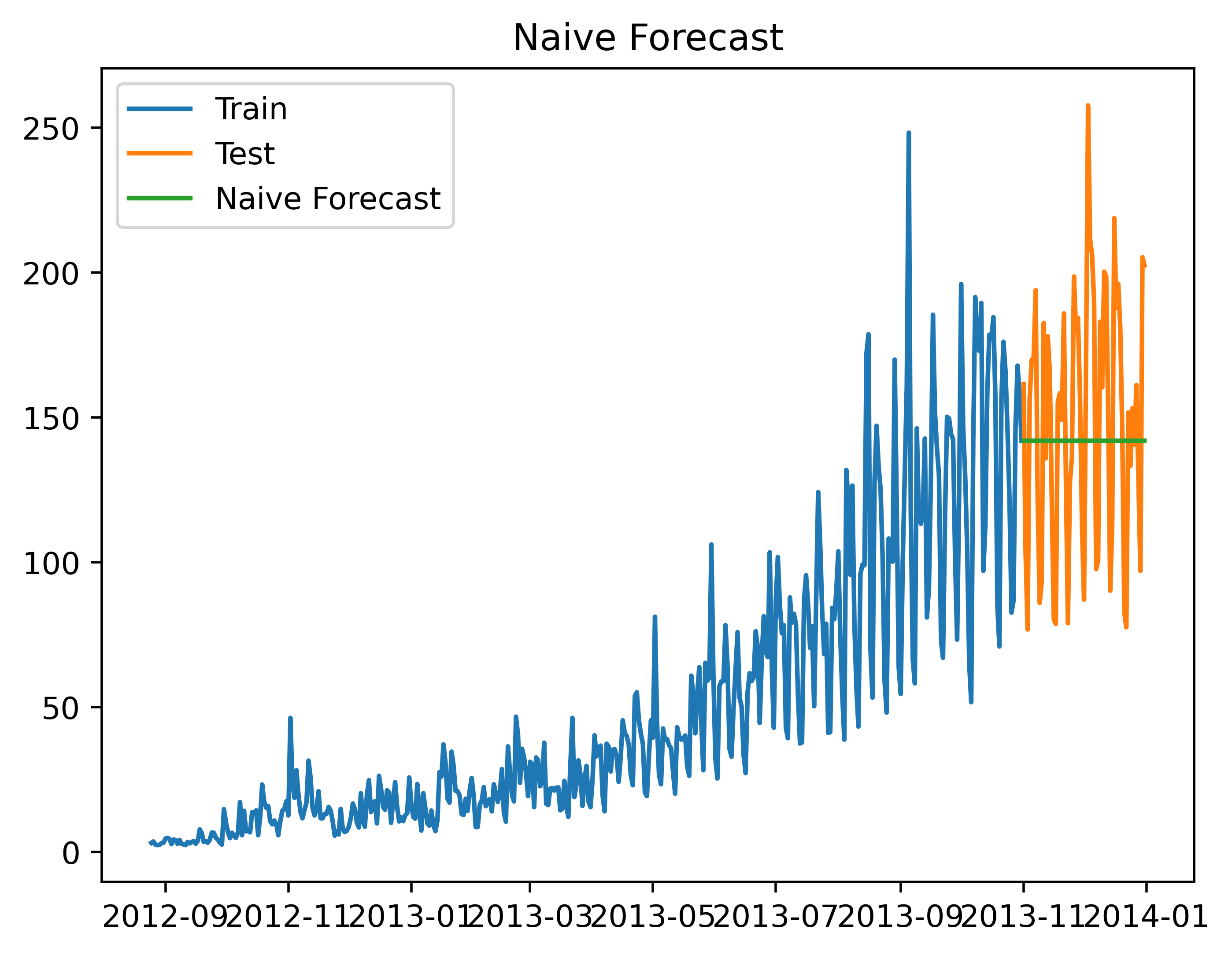
"""
朴素法到底有多大的误差呢?
我们计算下均方根误差,检查模型在测试数据集上的准确率,结果发现均方误差RMS=43.91640614391676
"""from sklearn.metrics import mean_squared_error
from math import sqrtrms = sqrt(mean_squared_error(test['Count'], y_hat['naive']))
print("均方误差RMS=",rms)6.时间预测序列经典算法2: 简单平均法
"""
经典算法2:简答平均法
对象的数值会随机上涨和下跌,平均值一般会比较稳定,保持一致。
我们经常会遇到一些数据集,虽然在一定时期内出现小幅变动,但每个时间段的平均值确实保持不变。
这种情况下,我们可以预测出第二天的预测值大致和过去天数的价格平均值一致。
这种将预期值等同于之前所有观测点的平均值的预测方法就叫简单平均法。
公式y(t+1)=sum(y(i))/n(i=1,2,3,4.....n)
"""y_hat_avg = test.copy()
y_hat_avg['avg_forecast'] = train['Count'].mean()
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['avg_forecast'], label='Average Forecast')
plt.legend(loc='best')
plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/时间序列3.png', dpi=500, bbox_inches='tight')
plt.show() 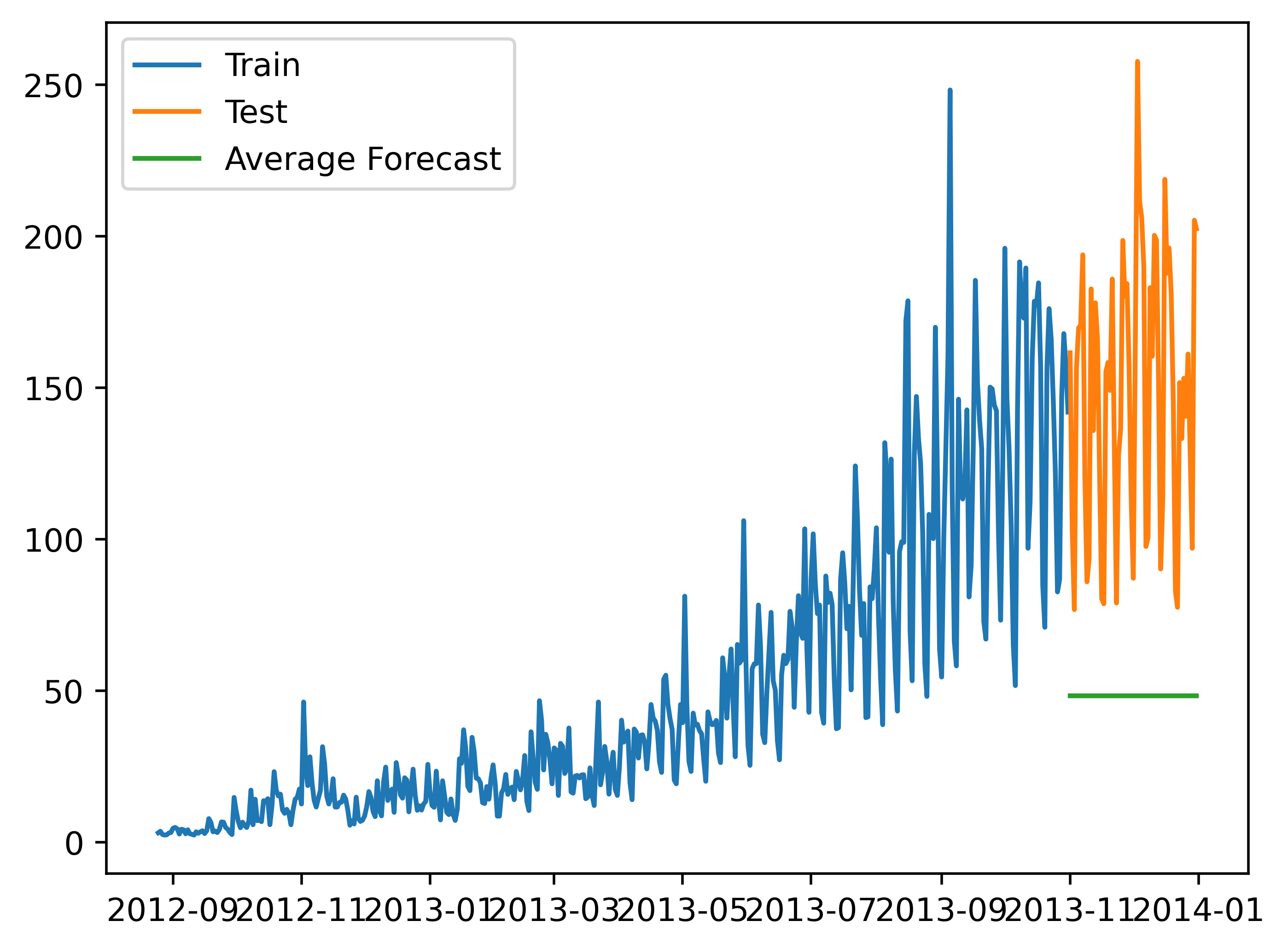
7.时间预测序列经典算法3:移动平均法
"""
经典算法3:移动平均法
研究的数据在一段时间内大幅上涨,但后来又趋于平稳。我们也经常会遇到这种数据集,比如价格或销售额某段时间大幅上升或下降。
这样的话对于整体平均数的计算的值显然是不合理的,因为极大极小的数已经影响到平均数合理的大小了。
如果我们这时用之前的简单平均法,就得使用所有先前数据的平均值,但在这里使用之前的所有数据是说不通的,因为用开始阶段的价格值会大幅影响接下来日期的预测值。
因此我们对于时间进行分段截取,分别计算切断时间的平均值,这样会显得更加合理一些。
很明显这里的逻辑是划分窗口区,这种用某些窗口期计算平均值的预测方法就叫移动平均法。
"""8.时间预测序列经典算法4:简单指数法
"""
经典算法四:简单指数法
我们注意到简单平均法和加权移动平均法在选取时间点的思路上存在较大的差异。
我们就需要在这两种方法之间取一个折中的方法,在将所有数据考虑在内的同时也能给数据赋予不同非权重。
例如,相比更早时期内的观测值,它会给近期的观测值赋予更大的权重。按照这种原则工作的方法就叫做简单指数平滑法。
它通过加权平均值计算出预测值,其中权重随着观测值从早期到晚期的变化呈指数级下降,最小的权重和最早的观测值相关:
这样可能早期的指数所占的权重就更大,越晚期的指数所占的权重就越小
这样的话我们就得出了如下的计算公式:y(t+1)=a*y(t)+(1-a)*y(t-1)
"""from statsmodels.tsa.api import SimpleExpSmoothingy_hat_avg = test.copy()
fit = SimpleExpSmoothing(np.asarray(train['Count'])).fit(smoothing_level=0.6, optimized=False)
y_hat_avg['SES'] = fit.forecast(len(test))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SES'], label='SES')
plt.legend(loc='best')
plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/时间序列4.png', dpi=500, bbox_inches='tight')
plt.show()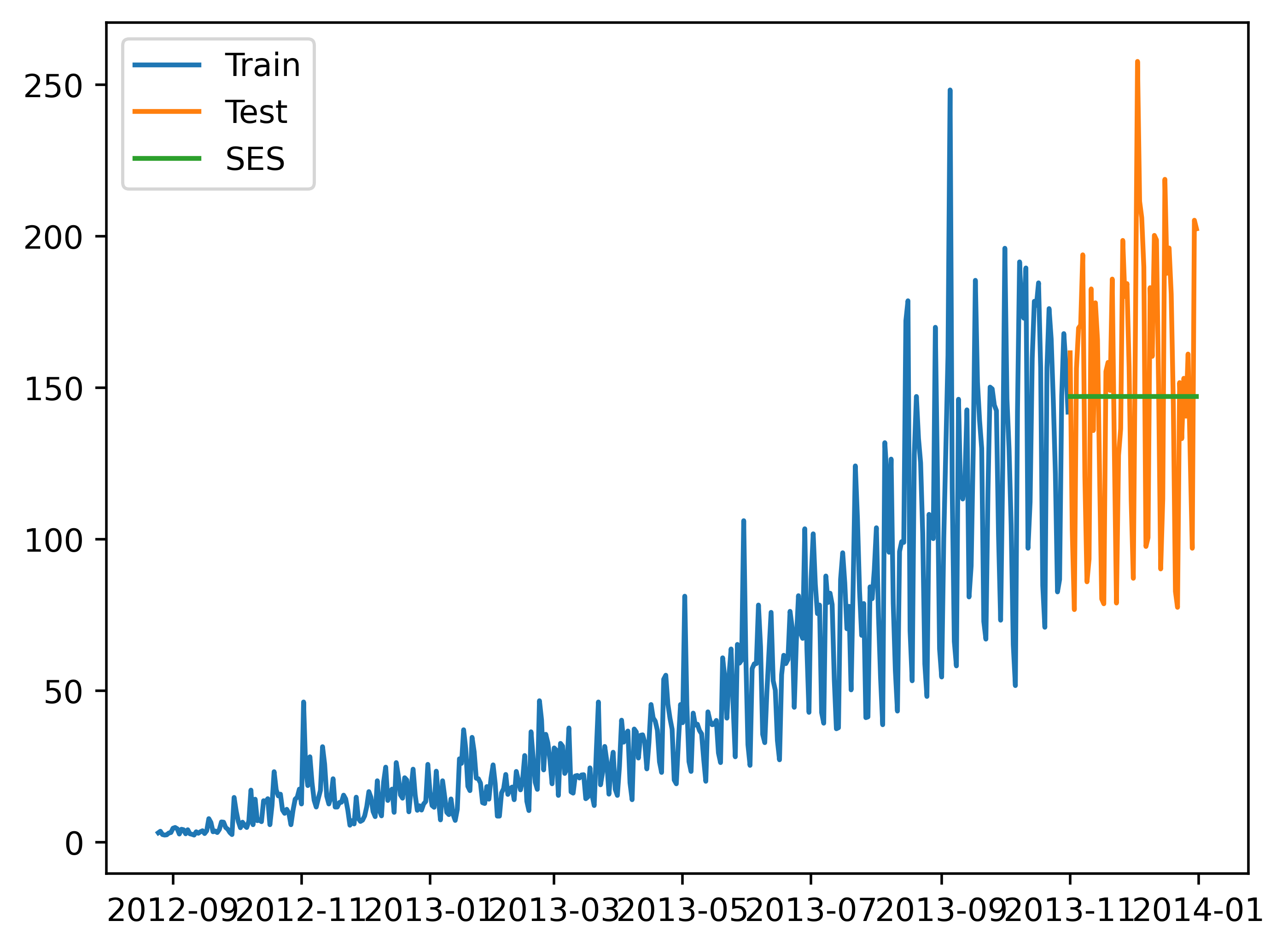
9.时间预测序列经典算法5:Holt线性趋势法
"""
经典算法5:Holt线性趋势法
如果物对象的观测值是呈不断上涨的总体趋势的,我们在一段时间内观察到的数值的总体的模式。
每个时序数据集可以被划分为为相应的几个部分:趋势(Trend),季节性(Seasonal)和残差(Residual)。
通Holt线性趋势法,我们可以预测任何时期呈现变化趋势的曲线的预测值
"""import statsmodels.api as sm
sm.tsa.seasonal_decompose(train['Count']).plot()
result = sm.tsa.stattools.adfuller(train['Count'])
plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/时间序列100.png', dpi=500, bbox_inches='tight')
plt.show()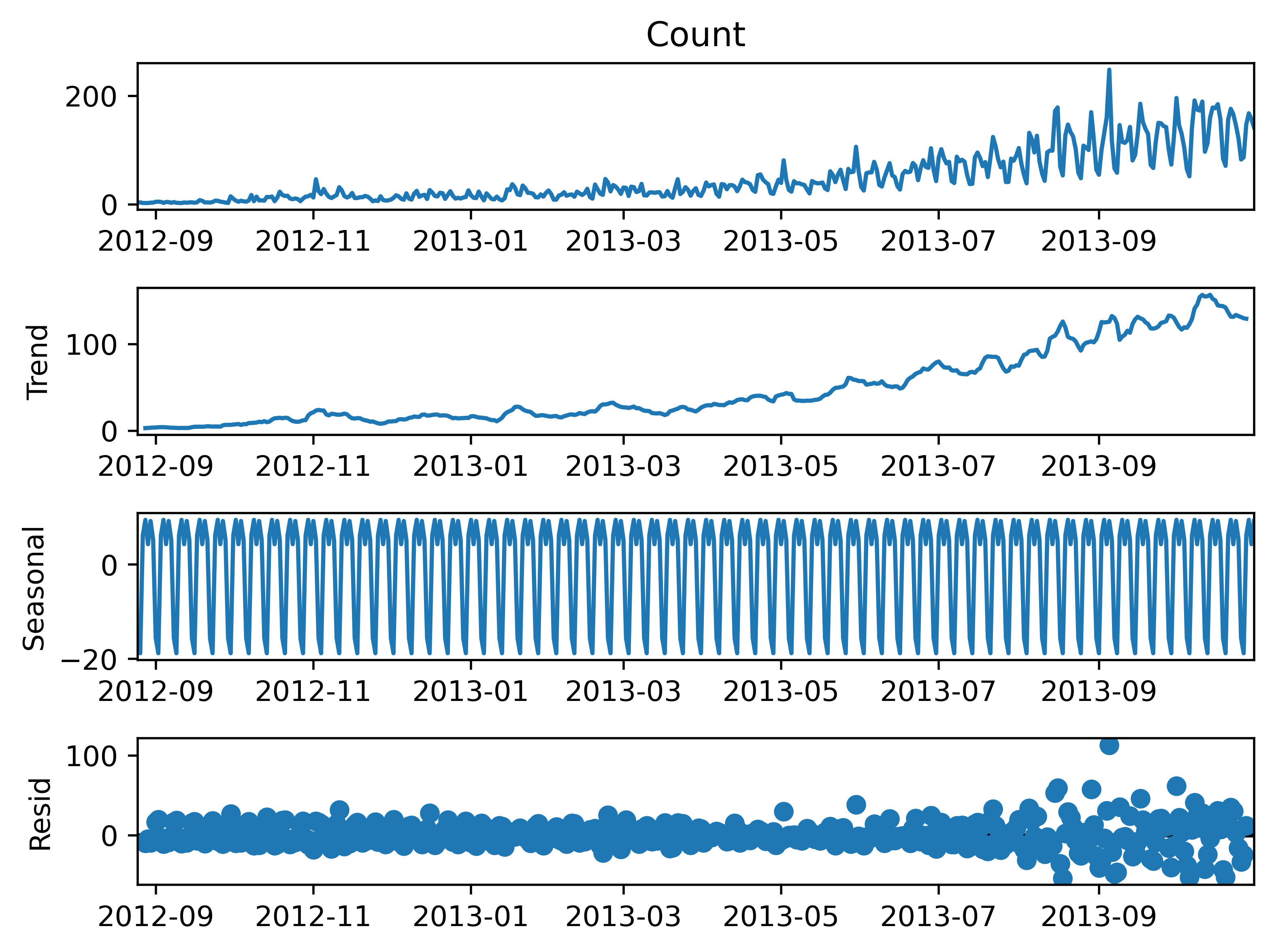
from statsmodels.tsa.api import Holty_hat_avg = test.copy()fit = Holt(np.asarray(train['Count'])).fit(smoothing_level=0.3, smoothing_slope=0.1)
y_hat_avg['Holt_linear'] = fit.forecast(len(test))plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['Holt_linear'], label='Holt_linear')
plt.legend(loc='best')
plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/时间序列6.png', dpi=500, bbox_inches='tight')
plt.show() 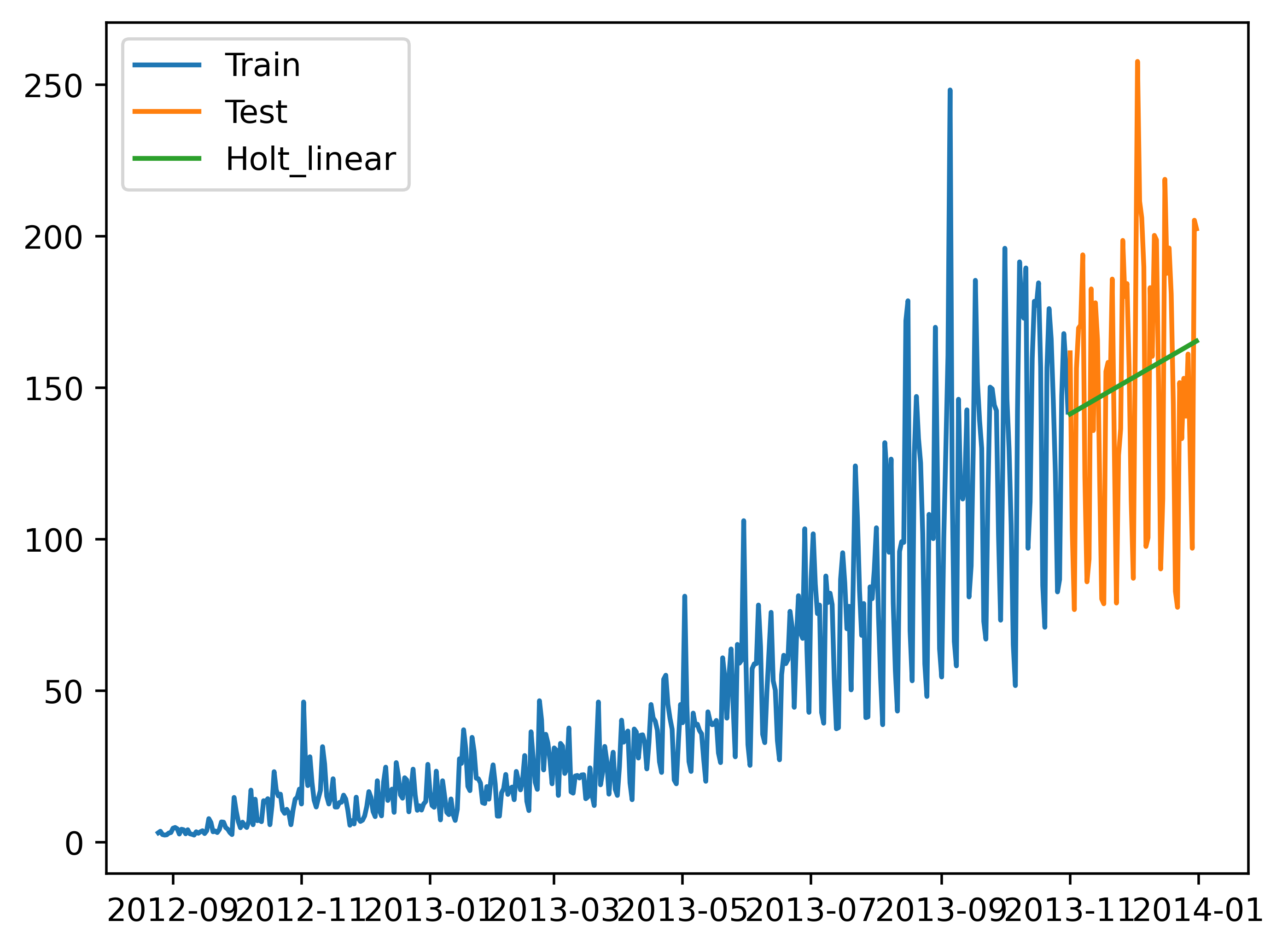
10.时间预测序列经典算法6:Holt-Winters季节性预测算法
"""
经典算法6:Holt-Winters季节性预测算法
我们之前在面临波动较大的数据的时候显得就是束手无策了,很显然前5种算法对于波动值的处理都不尽如人意!
所以造成了我们的预测有的时候就往往误差过大,预测不够精准!
我们之前讨论的5种模型在预测时并没有考虑到数据集的季节性,因此我们需要一种能考虑这种因素的方法。
应用到这种情况下的算法就叫做Holt-Winters季节性预测模型。
它是一种三次指数平滑预测,其背后的理念就是除了水平和趋势外,还将指数平滑应用到季节分量上。
Holt-Winters季节性预测模型由预测函数和三次平滑函数——一个是水平函数ℓt,一个是趋势函数bt,一个是季节分量 st,以及平滑参数α,β和γ。
在Holt-Winters算法中,我们采用的是相加和相乘的方法:
当季节性变化大致相同时,优先选择相加方法,
当季节变化的幅度与各时间段的水平成正比时,优先选择相乘的方法。
这样进行的预测值可能会更加合理一些!
"""from statsmodels.tsa.api import ExponentialSmoothingy_hat_avg = test.copy()
fit1 = ExponentialSmoothing(np.asarray(train['Count']), seasonal_periods=7, trend='add', seasonal='add', ).fit()
y_hat_avg['Holt_Winter'] = fit1.forecast(len(test))
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['Holt_Winter'], label='Holt_Winter')
plt.legend(loc='best')
plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/时间序列7.png', dpi=500, bbox_inches='tight')
plt.show()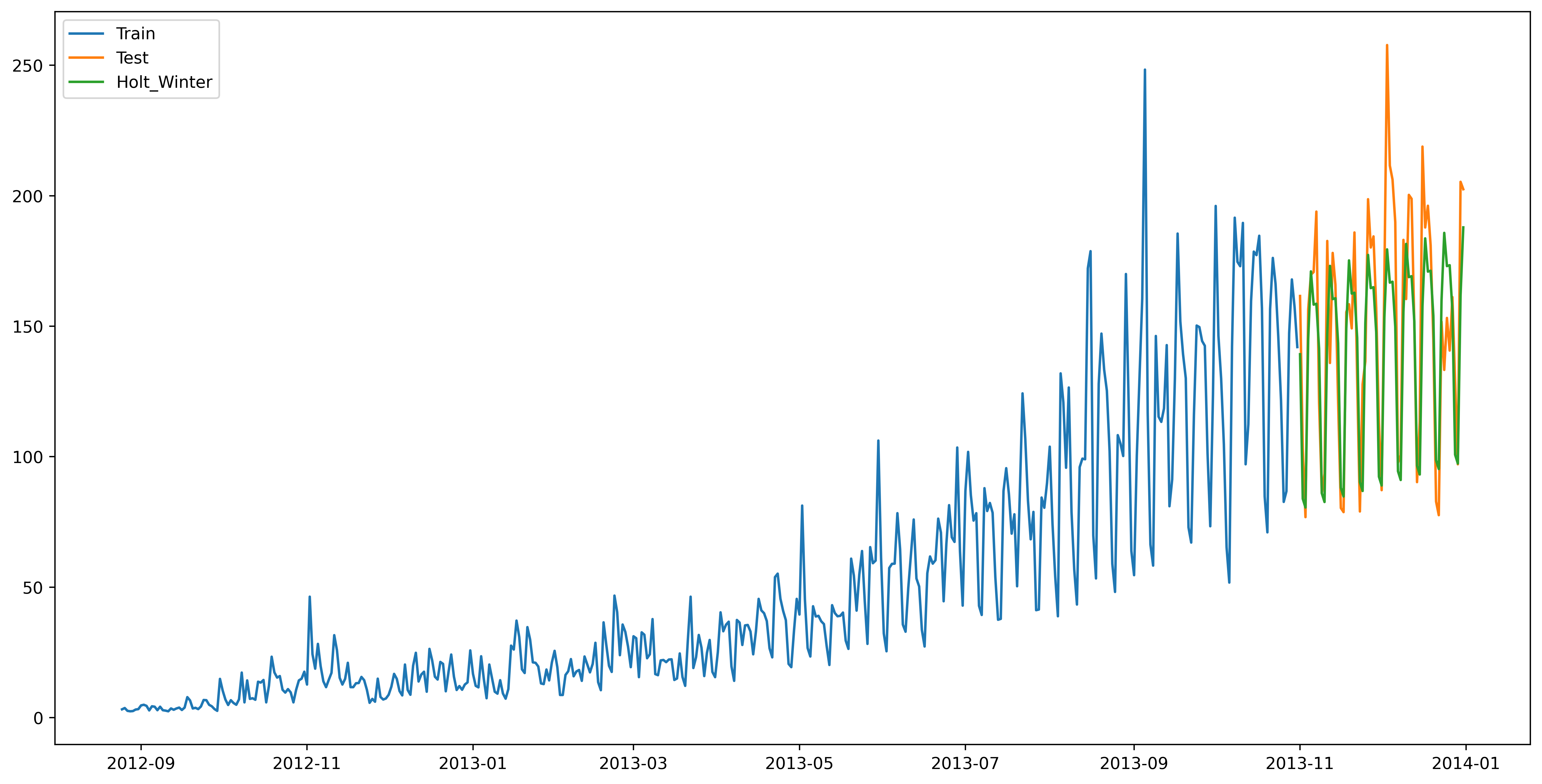
11.时间预测序列经典算法7:自回归移动平均(ARIMA)算法
"""
经典算法7:自回归移动平均(ARIMA)算法
ARIMA算法是前面提到的经典算法的集大成者,
首先我们考虑到可指数平滑模型都是基于数据中的趋势和季节性的描述,
同时我们考虑回归移动平均模型的目标是描述数据中彼此之间的关系。
综合的结果使得我们预测出来的值会更加的合理,预测值和对应的测试值拟合的越来越成功
"""import statsmodels.api as smy_hat_avg = test.copy()
fit1 = sm.tsa.statespace.SARIMAX(train.Count, order=(2, 1, 4), seasonal_order=(0, 1, 1, 7)).fit()
y_hat_avg['SARIMA'] = fit1.predict(start="2013-11-1", end="2013-12-31", dynamic=True)
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SARIMA'], label='SARIMA')
plt.legend(loc='best')
plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/时间序列8.png', dpi=500, bbox_inches='tight')
plt.show() 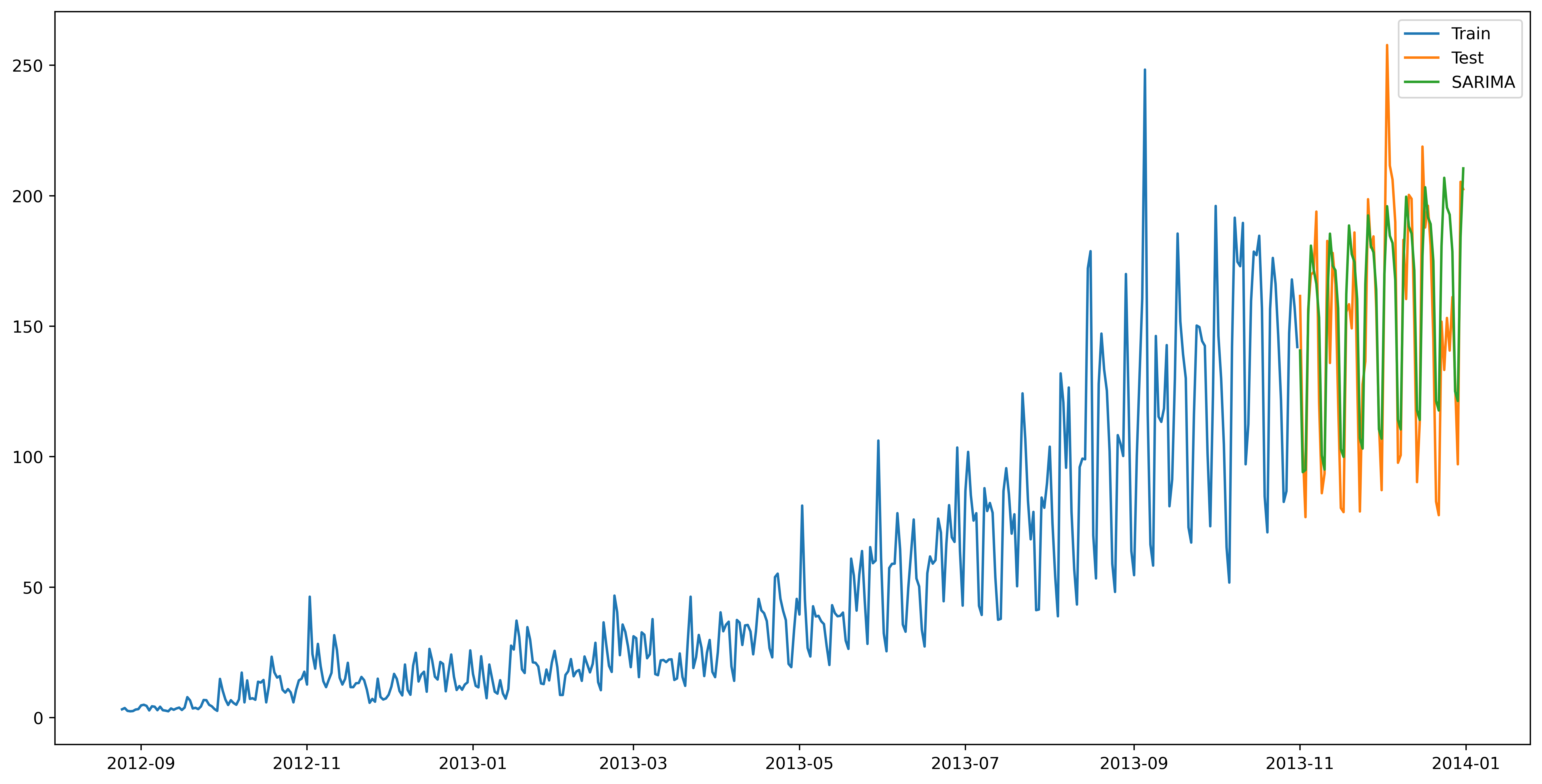
12.参考文章和致谢
"""
#参考文章和致谢:
首先代码主要来源于:https://www.cnblogs.com/lfri/articles/12243268.html#gallery-5
如果我在每一个算法中都有解释,如果还不能够明白,请跳转至原文章来进行学习,作者深入浅出的教学以及比较细致的类比和公式一定能过使你明白时间序列预测模型!
在这里我感谢这篇文章对我的帮助,首先是有完全的数据集可使用,其次是带我完整地进行了一次python的项目分析,使我受益匪浅!
再次感谢文章和作者对于我的启发和帮助!
"""相关文章:

数学建模--时间序列预测模型的七种经典算法的Python实现
目录 1.开篇版权提示 2.时间序列介绍 3.项目数据处理 4.项目数据划分可视化 5.时间预测序列经典算法1:朴素法 6.时间预测序列经典算法2: 简单平均法 7.时间预测序列经典算法3:移动平均法 8.时间预测序列经典算法4:简单指…...
nginx-反向代理缓存
反向代理缓存相当于自动化动静分离。 将上游服务器的资源缓存到nginx本地,当下次再有相同的资源请求时,直接讲nginx缓存的资源返回给客户端。 本地缓存资源有一个过期时间,当超过过期时间,则重新向上游服务器重新请求获取资源。…...

大模型重塑区域人才培养,飞桨(重庆)人工智能教育创新中心正式启动
2023年8月22日,重庆市高校人工智能产教融合院长研讨会暨飞桨(重庆)人工智能教育创新中心启动仪式在重庆大学成功召开。会上,由百度飞桨、重庆大学组织重庆市二十一所高校共建的飞桨(重庆)人工智能教育创新中…...

PAT 1164 Good in C 测试点3,4
个人学习记录,代码难免不尽人意。 When your interviewer asks you to write “Hello World” using C, can you do as the following figure shows? Input Specification: Each input file contains one test case. For each case, the first part gives the 26 …...
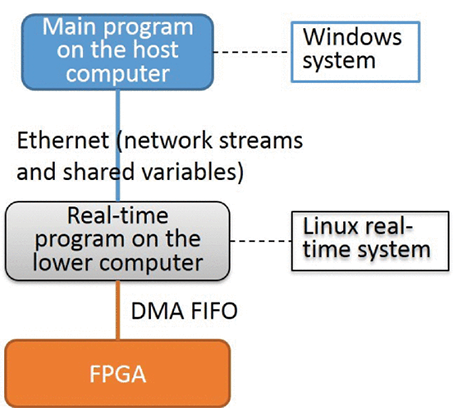
LabVIEW对EAST长脉冲等离子体运行的陀螺稳态运行控制
LabVIEW对EAST长脉冲等离子体运行的陀螺稳态运行控制 托卡马克是实现磁约束核聚变最有希望的解决方案之一。电子回旋共振加热(ECRH是一种对托卡马克有吸引力的等离子体加热方法,具有耦合效率高,功率沉积定位好等优点。陀螺加速器是ECRH系统中…...

Fragment
Fragment是Android开发中的一个重要组件,用于构建灵活且可重用的用户界面模块。它可以作为Activity的一部分来展示用户界面,并且可以嵌套在其他Fragment中,从而形成复杂的界面层级。 以下是一个简单的示例,展示了如何在Android中…...

哈希表-救赎金
Leetcode: https://leetcode.cn/problems/ransom-note/?envTypestudy-plan-v2&envIdtop-interview-150 给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。 如果可以,返回 true …...

vue3+vite+ts项目适配各种分辨率解决方案
现在的电脑屏幕和尺寸越来越多样化,对于前端开发来说,适配各种屏幕成了大难题,开发中一个实际例子:开发一个导航栏,ui给的是1920*60的尺寸,前端开发的时候,在自己电脑缩放比例中开发的ÿ…...
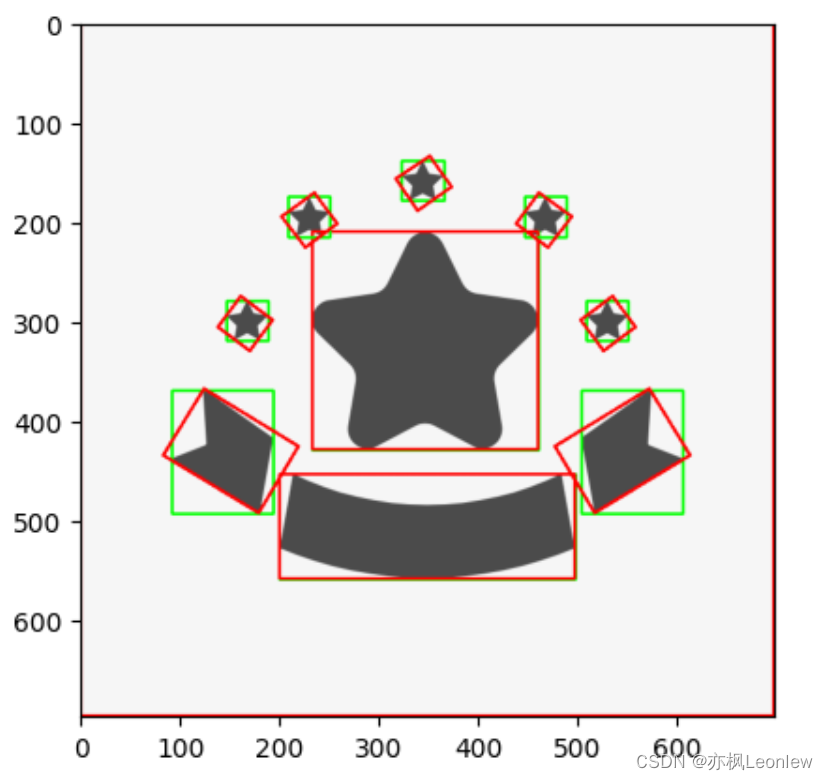
Python Opencv实践 - 矩形轮廓绘制(直边矩形,最小外接矩形)
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/stars.png") plt.imshow(img[:,:,::-1])img_gray cv.cvtColor(img, cv.COLOR_BGR2GRAY) #通过cv.threshold转换为二值图 ret,thresh cv.threshold(img_gray,…...

大数据HBASE的详细使用
摘要:本文将深入探讨大数据HBASE的使用步骤,帮助读者了解和掌握这一强大的分布式数据库系统的基本概念和操作技巧。通过本文的阅读,读者将能够熟悉HBASE的基本设置,了解其核心概念,掌握基本的查询和管理操作࿰…...
Sentinel 流量控制框架
1. Sentinel 是什么? Sentinel是由阿里中间件团队开源的,面向分布式服务架构的轻量级高可用流量控制组件。 2. 主要优势和特性 轻量级,核心库无多余依赖,性能损耗小。 方便接入,开源生态广泛。 丰富的流量控制场景。 …...

leetcode原题: 跳水板
题目: 你正在使用一堆木板建造跳水板。有两种类型的木板,其中长度较短的木板长度为shorter,长度较长的木板长度为longer。你必须正好使用k块木板。编写一个方法,生成跳水板所有可能的长度。 返回的长度需要从小到大排列。 示例&…...

深度学习入门(Python)学习笔记1
第1章 Python入门 1.1python是什么 Python是一个简单、易读、易记的编程语言,而且是开源的,可以免费地自由使用。 使用Python不仅可以写出可读性高的代码,还可以写出性能高(处理速度快)的代码。 再者,在…...
苏州想要获得融资融券低利率账户的方法?怎么开融资融券账户?
想要获得融资融券低利率账户,可以通过以下几种方式: 选择低费率的券商:不同券商的费率不同,一些券商会提供低利率的融资融券账户,可以通过咨询券商或者比较不同券商的费率来找到最佳账户。 提升自身信用:获…...

【LeetCode周赛】LeetCode第359场周赛
LeetCode第359场周赛 判别首字母缩略词k-avoiding 数组的最小总和销售利润最大化找出最长等值子数组 判别首字母缩略词 给你一个字符串数组 words 和一个字符串 s ,请你判断 s 是不是 words 的 首字母缩略词 。 如果可以按顺序串联 words 中每个字符串的第一个字符…...
vue3+ts+tinynce在富文本编辑器菜单栏实现下拉框选择
实现效果 代码: <script lang"ts" setup> import Editor from tinymce/tinymce-vue import tinymce from tinymce; import { getIndicator } from /api/data-assets/data-dictoryimport {computed, ref} from "vue"; const props defin…...

前端UI组件库深度解析:构建现代化的用户体验
引言 在当今的前端开发中,UI组件库已经成为了我们工具箱中不可或缺的一部分。这些库可以极大地提高我们的工作效率,同时也使我们能够专注于实现真正的业务逻辑,而不是重复地编写UI代码。本篇博客将详细地探讨UI组件库的核心概念,…...

leetcode 1326. Minimum Number of Taps to Open to Water a Garden
x轴上的花园范围为[0,n], 0~n这个n1个离散点上有水龙头,第 i 个水龙头能浇水的范围为[i-ranges[i], iranges[i]]. 求能浇整个花园的最小水龙头个数。 思路: 方法一: greedy 先把每个水龙头能浇的区间准备好, 用一个数组保存所有…...

C++日期类的基本实现
前言 对于许多出初学C的同学来说首先接触的第一个完整的类便是日期类,这个类能有效的帮助我们理解C中有关类的初始化以及重载的相关知识,帮助我们轻松上手体验C的魅力。 文章目录 前言一、日期类整体初概二、构造2.1 判断日期是否合法2.2 构造函数 三、…...

第六章:数据结构与算法-part3:数据结构算法提升
文章目录 一、排序算法1.1 插入排序1、直接插入排序2、折半插入排序3、希尔排序 1.2、交换排序法1、起泡排序2、快速排序 1.3 选择类排序1、简单选择排序 二、业务逻辑算法设计2.1 基本概念和术语2.2 静态查找表2.3、有序表的查找 一、排序算法 排序是数据处理过程中经常使用的…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
