leetcode 1326. Minimum Number of Taps to Open to Water a Garden

x轴上的花园范围为[0,n], 0~n这个n+1个离散点上有水龙头,第 i 个水龙头能浇水的范围为[i-ranges[i], i+ranges[i]].
求能浇整个花园的最小水龙头个数。
思路:
方法一:
greedy
先把每个水龙头能浇的区间准备好,
用一个数组保存所有区间,数组下标为区间起点,数组内容为区间终点。
然后从左到右遍历这个数组,到这里就和55题Jump Game类似了。
用一个变量canReach表示到目前的水龙头为止能浇到的最远距离。preEnd表示前一个水龙头的区间终点。
如果当前位置 > preEnd,说明需要开一个新的水龙头,
但是如果这时canReach <= preEnd(前一水龙头处能浇到的最远距离也无法到达当前位置,后面有说明),说明无法到达,返回-1.
更新preEnd到canReach (canReach这时还没有更新,即preEnd更新到前一个水龙头为止的最远范围). 水龙头个数+1.
把canReach更新到和当前区间终点相比的较大值。
有一个特殊情况要注意下,就是Example2中ranges[i]=0的情况。
注意能浇水到整个花园说明不止是离散点i , i+1, …能浇到,i 到 i+1之间的连续点部分也必须在区间中。
而ranges[i] = 0 表示只能浇到离散点 i 本身。比如1,2点能浇到,但它们之间的1.1, 1.2, …都不在浇灌范围。
所以在处理区间时,canReach必须能到达当前点才算满足条件。
public int minTaps(int n, int[] ranges) {int preEnd = 0;int canReach = 0;int[] startEnd = new int[n+1];int cnt = 0;for(int i = 0; i <= n; i++) {if(ranges[i] == 0) continue;int start = (i - ranges[i] < 0 ? 0 : i - ranges[i]);int end = (i + ranges[i] > n ? n : i + ranges[i]);startEnd[start] = end;}for(int i = 0; i <= n; i++) {if(i > preEnd) {if(canReach <= preEnd) return -1;cnt ++;preEnd = canReach;}if(startEnd[i] > canReach) canReach = startEnd[i];}//cnt是前一区间满足条件时在当前区间加的,最后一个区间没有下一区间去处理,所以要在最后处理一下//如果preEnd能到达最后位置,就不需要cnt+1,如果到不了,需要再cnt++,preEnd更新到canReachreturn cnt + (preEnd < n ? 1 : 0);}
方法二:
DP
dp[i ] 表示浇到 i 位置所需的水龙头个数。
开始的时候,除了dp[0],其他全部初始化为无穷大。
还是像上面一样从左到右计算每个水龙头的浇水区间。
区间内每个点处所需的最少水龙头个数dp[ i ] = min(dp[i], dp[区间的起点]+1).
这是什么意义呢?
因为dp[0]=0, 当更新水龙头0的区间时,都会以dp[0]+1为准,把0处的水龙头能浇到的范围内,每个点处所需水龙头个数更新为1.
假设第一个区间为[0,2],更新如下
1 1 1 Inf Inf Inf
这时假如进入下一区间[2,4],那么在2的位置,仍然可以保持dp[2]=min(dp[2], dp[2]+1)=1.
到了位置3时,dp[3]=min(Inf,dp[2]+1)就变成需要2个水龙头。
同样的,如果前一范围覆盖不到后面的区间,就会出现min(inf, inf+1)的情况。
最后返回dp[n], 如果dp[n]为Inf, 说明无法浇到整个花园,返回-1.
public int minTaps(int n, int[] ranges) {final int INF = 100000;int[] dp = new int[n+1];Arrays.fill(dp, INF);dp[0] = 0;for(int i = 0; i <= n; i++) {int start = (i-ranges[i] < 0 ? 0 : i-ranges[i]);int end = (i + ranges[i] > n ? n : i+ranges[i]);for(int j = start; j <= end; j++){dp[j] = Math.min(dp[j], dp[start]+1);}}return dp[n] == INF ? -1 : dp[n];}
相关文章:

leetcode 1326. Minimum Number of Taps to Open to Water a Garden
x轴上的花园范围为[0,n], 0~n这个n1个离散点上有水龙头,第 i 个水龙头能浇水的范围为[i-ranges[i], iranges[i]]. 求能浇整个花园的最小水龙头个数。 思路: 方法一: greedy 先把每个水龙头能浇的区间准备好, 用一个数组保存所有…...

C++日期类的基本实现
前言 对于许多出初学C的同学来说首先接触的第一个完整的类便是日期类,这个类能有效的帮助我们理解C中有关类的初始化以及重载的相关知识,帮助我们轻松上手体验C的魅力。 文章目录 前言一、日期类整体初概二、构造2.1 判断日期是否合法2.2 构造函数 三、…...

第六章:数据结构与算法-part3:数据结构算法提升
文章目录 一、排序算法1.1 插入排序1、直接插入排序2、折半插入排序3、希尔排序 1.2、交换排序法1、起泡排序2、快速排序 1.3 选择类排序1、简单选择排序 二、业务逻辑算法设计2.1 基本概念和术语2.2 静态查找表2.3、有序表的查找 一、排序算法 排序是数据处理过程中经常使用的…...

keras深度学习框架通过卷积神经网络cnn实现手写数字识别
昨天通过keras构建简单神经网络实现手写数字识别,结果在最后进行我们自己的手写数字识别的时候,准确率堪忧,只有60%。今天通过卷积神经网络来实现手写数字识别。 构建卷积神经网络和简单神经网络思路类似,只不过这里加入了卷积、池…...

Springboot启动异常 Command line is too long
Springboot启动异常 Command line is too long Springboot启动时直接报异常 Command line is too long. Shorten command line for xxxxxApplication or also for Spring Boot default解决方案: 修改 SystemApplication 的 Shorten command line,选择 JAR manife…...
PXE 装机(五十)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、PXE是什么 二、PXE的组件 三、配置vsftpd 四、配置tftp 五、准备pxelinx.0文件、引导文件、内核文件 六、配置dhcp 七、创建default文件 八、配置pxe无人值守…...

C++ 虚函数与纯虚函数
目录 1. 虚函数 2. 纯虚函数 C 中的虚函数和纯虚函数都是实现多态的重要机制。多态可以让不同的对象以相同的方式进行操作,从而简化代码的编写和维护。 1. 虚函数 虚函数是一种在基类中声明的函数,可以在派生类中进行重写。在运行时,根据对…...
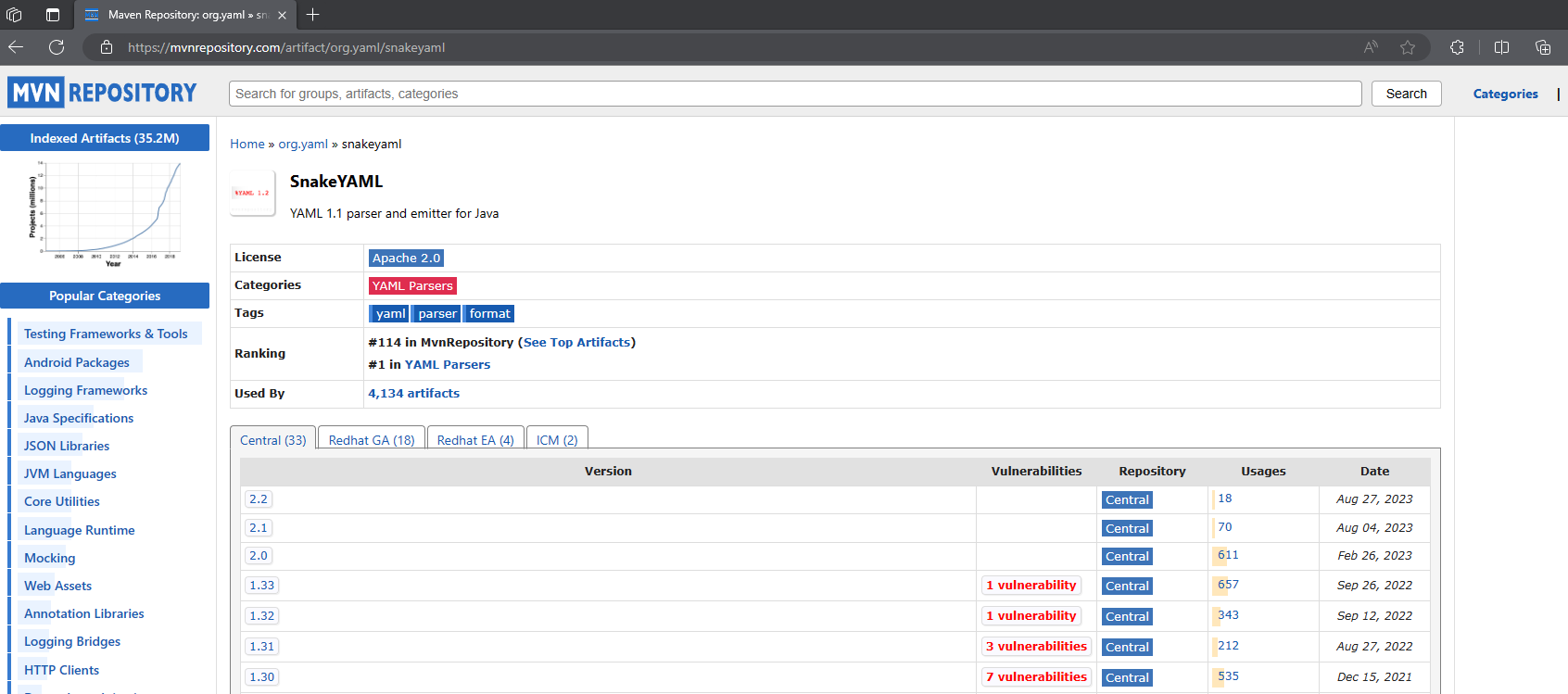
警告:Provides transitive vulnerable dependency maven:org.yaml:snakeyaml:1.30
1. 警告 SpringBoot 的 validation 依赖包含有易受攻击的依赖 snakeyaml。 警告信息如下: Provides transitive vulnerable dependency maven:org.yaml:snakeyaml:1.30 意思是:提供了可传递的易受攻击依赖 maven:org.yaml:snakeyaml:1.30 2. 警告示例 …...

中文命名实体识别
本文通过people_daily_ner数据集,介绍两段式训练过程,第一阶段是训练下游任务模型,第二阶段是联合训练下游任务模型和预训练模型,来实现中文命名实体识别任务。 一.任务和数据集介绍 1.命名实体识别任务 NER(Named En…...

WPF CommunityToolkit.Mvvm Messenger通讯
文章目录 环境WeakReferenceMessenger方法介绍无回调订阅发送Token区分有回调订阅发送 环境 CommunityToolkit.Mvvm Messenger 十月的寒流: 如何使用 CommunityToolkit.Mvvm 中的 Messenger 来进行 ViewModel 之间的通信 WeakReferenceMessenger 我这里只讲简单的弱Messenger…...

【杂言】写在研究生开学季
这两天搬进了深研院的宿舍,比中南的本科宿舍好很多,所以个人还算满意。受台风 “苏拉” 的影响,原本的迎新计划全部打乱,导致我现在都还没报道。刚开学的半个月将被各类讲座、体检以及入学教育等活动占满,之后又是比较…...

渗透测试漏洞原理之---【任意文件读取漏洞】
文章目录 1、概述1.1、漏洞成因1.2、漏洞危害1.3、漏洞分类1.4、任意文件读取1.4.1、文件读取函数1.4.2、任意文件读取 1.5、任意文件下载1.5.1、一般情况1.5.2、PHP实现1.5.3、任意文件下载 2、任意文件读取攻防2.1、路径过滤2.1.1、过滤../ 2.2、简单绕过2.2.1、双写绕过2.2.…...

合宙Air724UG LuatOS-Air LVGL API控件-图片 (Image)
图片 (Image) 图片IMG是用于显示图像的基本对象类型,图像来源可以是文件,或者定义的符号。 示例代码 -- 创建图片控件 img lvgl.img_create(lvgl.scr_act(), nil) -- 设置图片显示的图像 lvgl.img_set_src(img, "/lua/luatos.png") -- 图片…...
仿京东 项目笔记2(注册登录)
这里写目录标题 1. 注册页面1.1 注册/登录页面——接口请求1.2 Vue开发中Element UI的样式穿透1.2.1 ::v-deep的使用1.2.2 elementUI Dialog内容区域显示滚动条 1.3 注册页面——步骤条和表单联动 stepsform1.4 注册页面——滑动拼图验证1.5 注册页面——element-ui组件Popover…...

Spark与Flink的区别
分析&回答 (1)设计理念 1、Spark的技术理念是使用微批来模拟流的计算,基于Micro-batch,数据流以时间为单位被切分为一个个批次,通过分布式数据集RDD进行批量处理,是一种伪实时。 2、Flink是基于事件驱动的,是面向流的处理框架, Flink基于…...
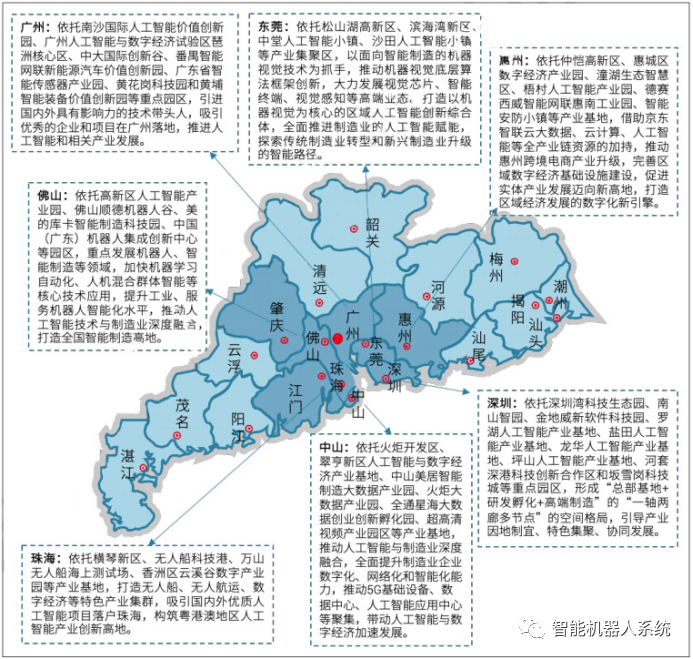
未来智造:珠三角引领人工智能产业集群
原创 | 文 BFT机器人 产业集群是指产业或产业群体在地理位置上集聚的现象,产业集群的研究对拉动区域经济发展,提高区域产业竞争力具有重要意义。 从我国人工智能产业集群形成及区域布局来看,我国人工智能产业发展主要集聚在京津冀、长三角、…...

【Unity db】sqlite
背景 最近使用unity,需要用到sqlite,记录下使用过程 需要的动态库 Mono.Data.Sqlite.dll,这个文件下载参考下面链接 SqliteConnection的Close和Open 连接的概念: 在数据库编程中,连接是一个重要的概念,…...
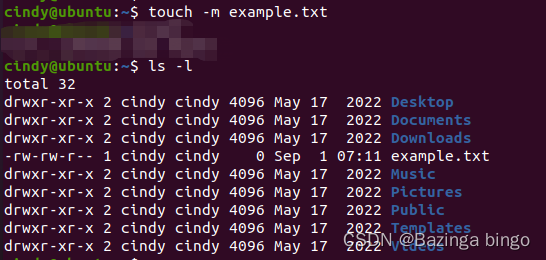
Linux 指令心法(四)`touch` 创建一个新的空文件
文章目录 命令的概述和用途命令的用法命令行选项和参数的详细说明命令的示例命令的注意事项或提示 命令的概述和用途 touch 是一个用于在 Linux 和 Unix 系统中创建空文件或更改现有文件的访问和修改时间的命令。如果指定的文件不存在,touch会创建一个新的空文件&a…...
分类算法系列②:KNN算法
目录 KNN算法 1、简介 2、原理分析 数学原理 相关公式及其过程分析 距离度量 k值选择 分类决策规则 3、API 4、⭐案例实践 4.1、分析 4.2、代码 5、K-近邻算法总结 🍃作者介绍:准大三网络工程专业在读,努力学习Java,涉…...

12. 微积分 - 梯度积分
Hi,大家好。我是茶桁。 上一节课,我们讲了方向导数,并且在最后留了个小尾巴,是什么呢?就是梯度。 我们再来回看一下但是的这个式子: [ f x f y...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
