分类算法系列②:KNN算法
目录
KNN算法
1、简介
2、原理分析
数学原理
相关公式及其过程分析
距离度量
k值选择
分类决策规则
3、API
4、⭐案例实践
4.1、分析
4.2、代码
5、K-近邻算法总结
🍃作者介绍:准大三网络工程专业在读,努力学习Java,涉猎深度学习,积极输出优质文章
⭐分类算法系列①:初识概念
KNN算法
定义:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
来源:KNN算法最早是由Cover和Hart提出的一种分类算法
1、简介
K最近邻(K-Nearest Neighbors,KNN)是一种简单但强大的监督学习算法,用于分类和回归任务。它的基本思想是:给定一个新的数据点,通过找到训练数据中最接近它的K个邻居,来进行分类或回归预测。KNN算法在许多实际问题中表现良好,但也有其局限性。
以下是KNN算法的基本工作原理:
- 数据表示: 对于每个样本,KNN使用一组特征来描述。这些特征可以是数值、类别或其他类型的数据。每个样本都由特征向量表示。
- 距离度量: KNN算法使用某种距离度量来计算数据点之间的相似性。常用的距离度量包括欧几里德距离、曼哈顿距离等。对于每个样本,都可以计算其与训练数据中其他样本之间的距离。
- 邻居选择: 对于一个新的数据点,KNN算法会计算它与训练数据中所有数据点的距离,并选择最近的K个邻居。这些邻居通常是距离最近的K个训练样本。
- 预测(分类问题): 对于分类问题,KNN算法会将这K个最近邻居的类别进行统计,然后将新数据点分类为在这些邻居中占多数的类别。这就是所谓的“多数投票”法。
- 预测(回归问题): 对于回归问题,KNN算法会将这K个最近邻居的目标值(即回归目标)进行平均,然后将新数据点的回归预测设置为这个平均值。
KNN算法的优点包括简单易用、适用于多类别分类、不需要训练阶段(直接存储训练数据)等。
然而,KNN算法也有一些缺点,包括:
- 效率问题:对于大规模数据集,计算所有样本之间的距离可能会很耗时。
- 高维数据:在高维特征空间中,距离计算变得困难,且容易出现维度灾难(curse of dimensionality)。
- 需要合适的距离度量和K值的选择。
在实际应用中,选择适当的K值、距离度量和数据预处理方法非常重要,以确保KNN算法的性能最优化。
2、原理分析
数学原理
K-近邻(K-Nearest Neighbors,KNN)算法背后的数学原理涉及距离度量、邻居选择和预测的计算。以下是KNN算法的数学原理的详细解释:
- 距离度量: KNN算法中最重要的概念之一是距离度量,它用于衡量样本之间的相似性。常用的距离度量包括欧几里德距离(Euclidean distance)和曼哈顿距离(Manhattan distance)。
- 邻居选择: 对于一个新的数据点,KNN算法计算它与训练数据中所有数据点之间的距离。然后,它选择距离最近的K个数据点作为最近邻居。这些最近邻居可以根据计算的距离值进行排序。
- 预测(分类问题): 对于分类问题,KNN算法会统计这K个最近邻居中每个类别的数量。然后,将新数据点分类为在这些邻居中占多数的类别。
- 预测(回归问题): 对于回归问题,KNN算法会计算这K个最近邻居的目标值的平均值,然后将新数据点的回归预测设置为这个平均值。
在实际应用中,选择适当的K值以及距离度量方法非常重要。K值较小可能会导致模型过拟合,而K值较大可能会导致模型欠拟合。同时,距离度量的选择应根据数据的特点进行调整,以确保能够捕获数据之间的相似性。在高维空间中,可能需要对特征进行标准化以避免某些特征对距离的影响过大。
相关公式及其过程分析
k 近邻法 (k-nearest neighbor, k-NN) 是一种基本分类与回归方法。是数据挖掘技术中原理最简单的算法之一,核心功能是解决有监督的分类问题。KNN能够快速高效地解决建立在特殊数据集上的预测分类问题,但其不产生模型,因此算法准确 性并不具备强可推广性。
k近邻法 的输入为实例的特征向量,对应与特征空间的点;输出为实例的类别,可以取多类。
k近邻法 三个基本要素:k 值的选择、距离度量及分类决策规则。
算法过程:
1, 计算训练样本和测试样本中每个样本点的距离(常见的距离度量有欧式距离,马氏距离等);
2, 对上面所有的距离值进行排序;
3, 选前k个最小距离的样本;
4, 根据这k个样本的标签进行投票,得到最后的分类类别;
输入:训练数据集 :
其中, 为实例的特征向量,
为实例的类别,
输出:实例 x 所属的类 y
(1)根据给定的距离度量,在训练集 T 中找出与x最近邻的个点,涵盖这个 k 点的 x 的邻域记作
(2)在 中根据分类决策规则(如多数决策)决定 x 的类别 y:
其中,为指示函数,即
时
为1,否则
为0
距离度量
特征空间中两个实例点的距离时两个实例点相似程度的反映。
在距离类模型,例如KNN中,有多种常见的距离衡量方法。 如欧几里得距离、曼哈顿距离、闵科夫斯基距离、切比雪夫距离及余弦距离。其中欧几里得距离为最常见。
下面是几种距离的论述:
①欧几里得距离(Euclidean Distance):定义与欧几里得空间中,两点之间或多点之间的距离表示又称欧几里得度量。
二维平面:
三维空间:
推广到在n维空间中,有两个点A和B,两点的坐标分别为:
坐标轴上的值 正是样本数据上的n个特征。
②曼哈顿距离(Manhattan Distance):正式意义为城市区块距离,也被称作街道距离,该距离在欧几里得空间的固定直角坐标所形成的线段产生的投影的距离总和。
其计算方法相当于是欧式距离的1次方表示形式,其基本计算公式如下:
③闵科夫斯基距离(Minkowski Distance):闵氏距离不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述。
无论是欧式距离还是曼哈顿距离,都可视为闵可夫斯基距离的一种特例。
公式如下:
其中p是一个变参数:
当p=1时,就是曼哈顿距离;
当p=2时,就是欧氏距离;
当p→∞时,就是切比雪夫距离。
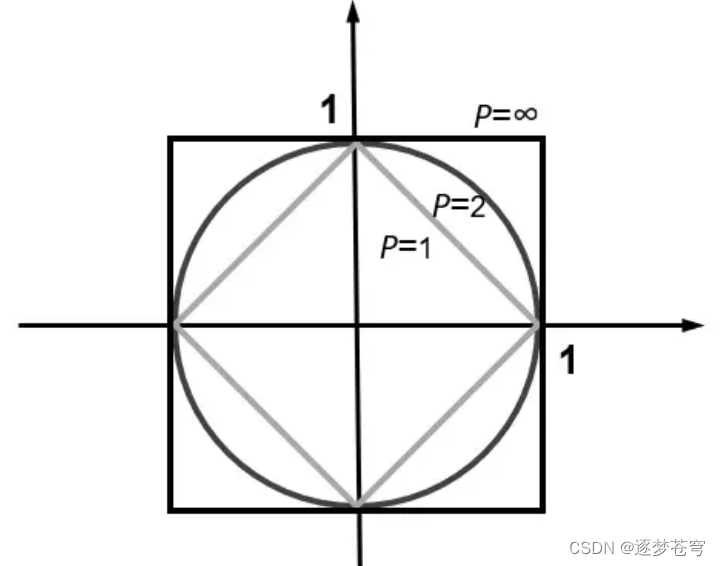
因此,根据变参数的不同,闵氏距离可以表示某一类 / 种的距离。
④切比雪夫距离(Chebyshev Distance):国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
二维平面:
n维空间:
⑤余弦距离:余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个样本差异的大小。
余弦值越接近1,说明两个向量夹角越接近0度,表明两个向量越相似。
几何中,夹角余弦可用来衡量两个向量方向的差异;
机器学习中,借用这一概念来衡量样本向量之间的差异。
公式:
k值选择
k 值的选择会对KNN 算法的结果产生重大影响。
- k 值的减小就意味着整体模型变得复杂,器容易受到由于训练数据中的噪声而产生的过分拟合的影响。
- k 值的的增大就意味着整体的模型变得简单。如果k太大,最近邻分类器可能会将测试样例分类错误,因为k个最近邻中可能包含了距离较远的,并非同类的数据点。
在应用中,k 值一般选取一个较小的数值,通常采用交叉验证来选取最优的k 值。
分类决策规则
根据 "少数服从多数,一 点算一票" 的原则进行判断,数量最多标签类别就是x的标签类别。其中涉及到的原理是"越相近越相似",这也是KNN 的基本假设。
3、API
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
- n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数
- algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},
- 可选用于计算最近邻居的算法:‘ball_tree’将会使用 BallTree,
- ‘kd_tree’将使用 KDTree。
- ‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。
(不同实现方式影响效率)
4、⭐案例实践
案例:预测签到位置:

数据介绍(train.csv和test.csv ):将根据用户的位置,准确性和时间戳预测用户正在查看的业务。
数据各项介绍:
row_id:登记事件的ID
x / y:坐标
accuracy性:定位准确性
time:时间戳
place_id:业务的ID,这是预测的目标
官网:https://www.kaggle.com/navoshta/grid-knn/data
4.1、分析
- 基本处理
- 缩小数据集范围 DataFrame.query()
- 删除没用的日期数据 DataFrame.drop(可以选择保留)
- 将签到位置少于n个用户的删除place_count = data.groupby('place_id').count()tf = place_count[place_count.row_id > 3].reset_index()data = data[data['place_id'].isin(tf.place_id)]
- 分割数据集
- 标准化处理
- k-近邻预测
4.2、代码
代码如下:
# -*- coding: utf-8 -*-
# @Author:︶ㄣ释然
# @Time: 2023/8/30 23:48
import pandas as pd
from sklearn.model_selection import train_test_split # 将数据集分割为训练集和测试集。
from sklearn.neighbors import KNeighborsClassifier # 实现KNN分类器
from sklearn.preprocessing import StandardScaler # 特征标准化'''
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选用于计算最近邻居的算法:‘ball_tree’将会使用 BallTree,‘kd_tree’将使用 KDTree。‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。(不同实现方式影响效率)
'''
def knncls():"""K近邻算法预测入住位置类别:return:"""# 一、处理数据以及特征工程# 1、读取收,缩小数据的范围data = pd.read_csv("./data/FBlocation/train.csv")# 数据逻辑筛选操作 df.query()data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")# 删除time这一列特征data = data.drop(['time'], axis=1)print(data)# 删除入住次数少于三次位置place_count = data.groupby('place_id').count()tf = place_count[place_count.row_id > 3].reset_index()data = data[data['place_id'].isin(tf.place_id)]# 3、取出特征值和目标值y = data['place_id']# y = data[['place_id']]x = data.drop(['place_id', 'row_id'], axis=1)# 4、数据分割与特征工程?# (1)、数据分割x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)# (2)、标准化std = StandardScaler()# 队训练集进行标准化操作x_train = std.fit_transform(x_train)print(x_train)# 进行测试集的标准化操作x_test = std.fit_transform(x_test)# 二、算法的输入训练预测# K值:算法传入参数不定的值 理论上:k = 根号(样本数)# K值:后面会使用参数调优方法,去轮流试出最好的参数[1,3,5,10,20,100,200]knn = KNeighborsClassifier(n_neighbors=3)# 调用fit()knn.fit(x_train, y_train)# 预测测试数据集,得出准确率y_predict = knn.predict(x_test)print("预测测试集类别:", y_predict)print("准确率为:", knn.score(x_test, y_test))if __name__ == '__main__':knncls()执行结果:
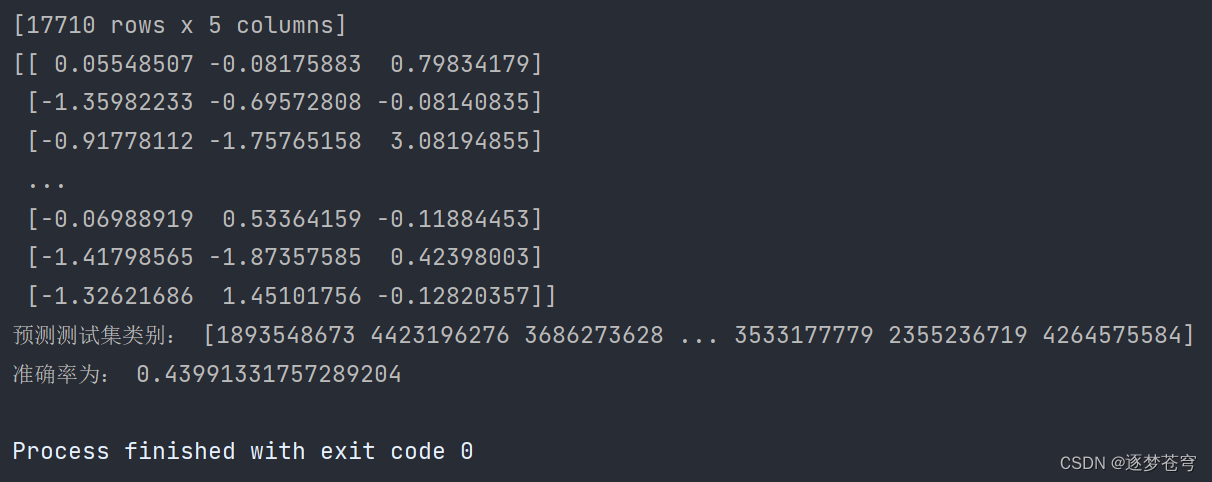
这段代码是一个使用K最近邻(KNN)算法进行分类预测的示例,用于预测移动设备的位置类别。下面逐行解释代码的每个部分:
- 导入必要的包:
- import pandas as pd:导入Pandas库,用于数据处理和分析。
- from sklearn.model_selection import train_test_split:从scikit-learn中导入train_test_split函数,用于将数据集分割为训练集和测试集。
- from sklearn.neighbors import KNeighborsClassifier:从scikit-learn中导入KNeighborsClassifier类,用于实现KNN分类器。
- from sklearn.preprocessing import StandardScaler:从scikit-learn中导入StandardScaler类,用于特征标准化。
- 函数knncls()定义:
- 该函数实现了一个完整的KNN分类流程。
- 数据读取与预处理:
- data = pd.read_csv("./data/FBlocation/train.csv"):从CSV文件读取数据。
- data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75"):对数据进行逻辑筛选,选取特定范围内的数据。
- data = data.drop(['time'], axis=1):删除数据中的时间列。
- place_count = data.groupby('place_id').count():根据位置ID对数据进行分组统计。
- tf = place_count[place_count.row_id > 3].reset_index():选取入住次数超过3次的位置。
- data = data[data['place_id'].isin(tf.place_id)]:筛选出入住次数较多的位置。
- 数据分割与特征工程:
- y = data['place_id']:目标值为位置ID。
- x = data.drop(['place_id', 'row_id'], axis=1):特征值为除位置ID和行ID外的其他特征。
- x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3):将数据集分割为训练集和测试集。
- std = StandardScaler():实例化一个标准化器。
- x_train = std.fit_transform(x_train):对训练集进行标准化操作。
- x_test = std.fit_transform(x_test):对测试集进行标准化操作。
- KNN模型训练与预测:
- knn = KNeighborsClassifier(n_neighbors=1):实例化一个KNN分类器,其中n_neighbors参数设置为1。
- knn.fit(x_train, y_train):训练KNN模型。
- y_predict = knn.predict(x_test):使用训练好的模型进行预测。
- print("准确率为:", knn.score(x_test, y_test)):输出模型在测试集上的准确率。
总体而言,这段代码演示了如何使用KNN算法进行分类预测。它包括数据读取、预处理、特征工程、模型训练和预测等步骤。同时,还使用了StandardScaler进行特征标准化,以及KNN分类器进行预测并计算准确率。
5、K-近邻算法总结
优点:简单,易于理解,易于实现,无需训练
缺点:
懒惰算法,对测试样本分类时的计算量大,内存开销大
必须指定K值,K值选择不当则分类精度不能保证
使用场景:小数据场景,几千~几万样本,具体场景具体业务去测试
相关文章:

分类算法系列②:KNN算法
目录 KNN算法 1、简介 2、原理分析 数学原理 相关公式及其过程分析 距离度量 k值选择 分类决策规则 3、API 4、⭐案例实践 4.1、分析 4.2、代码 5、K-近邻算法总结 🍃作者介绍:准大三网络工程专业在读,努力学习Java,涉…...

12. 微积分 - 梯度积分
Hi,大家好。我是茶桁。 上一节课,我们讲了方向导数,并且在最后留了个小尾巴,是什么呢?就是梯度。 我们再来回看一下但是的这个式子: [ f x f y...

Large Language Models and Knowledge Graphs: Opportunities and Challenges
本文是LLM系列的文章,针对《Large Language Models and Knowledge Graphs: Opportunities and Challenges》的翻译。 大语言模型和知识图谱:机会与挑战 摘要1 引言2 社区内的共同辩论点3 机会和愿景4 关键研究主题和相关挑战5 前景 摘要 大型语言模型&…...

Python操作Excel教程(图文教程,超详细)Python xlwings模块详解,
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「推荐专栏」:小白零基础《Python入门到精通》 xlwings模块详解 1、快速入门1、打开Excel2、创建工作簿2.1、使用工作簿2.2、操作…...

Java入门
Java导入包 import 主要用于导入在使用类前准备好了Import 关键字可以多次使用,导入多个包Import 关键字可以多次使用,导入多个类如果同一个包中需要大量的类,那么可以使用通配符进行导入如果Import了不同包,相同名称的类&#x…...
深度解析BERT:从理论到Pytorch实战
本文从BERT的基本概念和架构开始,详细讲解了其预训练和微调机制,并通过Python和PyTorch代码示例展示了如何在实际应用中使用这一模型。我们探讨了BERT的核心特点,包括其强大的注意力机制和与其他Transformer架构的差异。 关注TechLead&#x…...
小程序数据导出文件
小程序josn数据生成excel文件 先从下载传送门将xlsx.mini.min.js拷贝下来,新建xlsx.js文件放入小程序项目文件夹下。 const XLSX require(./xlsx)//在需要用的页面中引入// 定义导出 Excel 报表的方法exportData() {const that thislet newData [{time:2021,val…...

hadoop1.2.1伪分布式搭建
0.使用host-only方式 将Windows上的虚拟网卡改成跟Linux上的网卡在同一网段 注意:一定要将widonws上的WMnet1的IP设置和你的虚拟机在同一网段,但是IP不能相同 1.Linux环境配置(windows下面的防火墙也要关闭) 1.1修改主…...

【校招VIP】前端JavaScript语言之跨域
考点介绍: 什么是跨域?浏览器从一个域名的网页去请求另一个域名的资源时,域名、端口、协议任一不同,都是跨域。跨域是前端校招的一个重要考点,在面试过程中经常遇到,需要着重掌握。本期分享的前端算法考点之…...

mysql调优小计
1.选择最合适的字段属性:类型、⻓度、是否允许NULL等;尽量把字段设为not null,⼀⾯查询时对⽐是否为null; 2.要尽量避免全表扫描,⾸先应考虑在 where 及 order by 涉及的列上建⽴索引。 3.应尽量避免在 where ⼦句中对…...

AI:04-基于机器学习的蘑菇分类
蘑菇是一类广泛分布的真菌,其中许多种类具有重要的食用和药用价值,但也存在着一些有毒蘑菇。因此,准确地区分可食用和有毒的蘑菇对于保障人们的食品安全和健康至关重要。本研究旨在基于机器学习技术开发一种蘑菇分类系统,以实现对蘑菇的自动分类和识别。通过构建合适的数据…...
算法——排序
排序 下面的代码会用到宏定义,因为再C中没有swap交换函数,所以对于swap的宏定义代码如下: #define swap(a, b) {\__typeof(a) __a a; a b; b __a;\ } 稳定排序: 1.插入排序: 插入排序会将数组,分位两个部…...
leetCode动态规划“不同路径II”
迷宫问题是比较经典的算法问题,一般可以用动态规划、回溯等方法进行解题,这道题目是我昨晚不同路径这道题趁热打铁继续做的,思路与原题差不多,只是有需要注意细节的地方,那么话不多说,直接上coding和解析&a…...

100天精通Python(可视化篇)——第99天:Pyecharts绘制多种炫酷K线图参数说明+代码实战
文章目录 专栏导读一、K线图介绍1. 说明2. 应用场景 二、配置说明三、K线图实战1. 普通k线图2. 添加辅助线3. k线图鼠标缩放4. 添加数据缩放滑块5. K线周期图表 书籍推荐 专栏导读 🔥🔥本文已收录于《100天精通Python从入门到就业》:本专栏专…...

哈希表与有序表
哈希表与有序表 Set结构 key Map结构 key-value 哈希表 哈希表的时间复杂度都是常数项级别的,但常数较大 增删改查的时间都是常数级别的,与数据量无关 当哈希表存储的值是基础数据类型(Integer - int),哈希表中内…...

什么时候使用RPA?如何使用RPA?需要什么样的硬件支持?需要安装哪些软件?
RPA(Robotic Process Automation)是一种用于自动化执行重复性任务的技术,它可以帮助企业提高工作效率,降低人力成本,并减少人为错误。RPA适用于各种行业和场景,例如财务、人力资源、客户服务、IT运维等。 …...
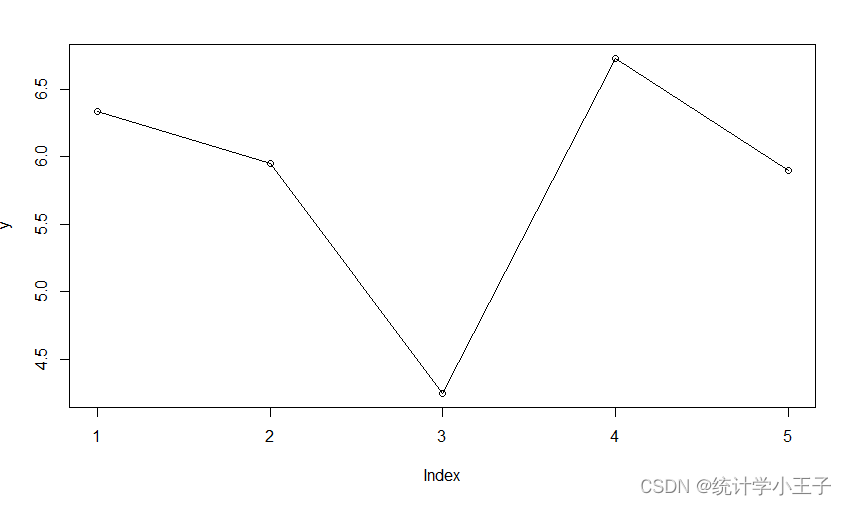
R语言入门——line和lines的区别
目录 0 引言一、 line()二、 lines() 0 引言 首先,从直观上看,lines比line多了一个s,但它们还是有很大的区别的,下面将具体解释这个两个函数的区别。 一、 line() 从R语言的帮助文档中找到,line()的使用,…...
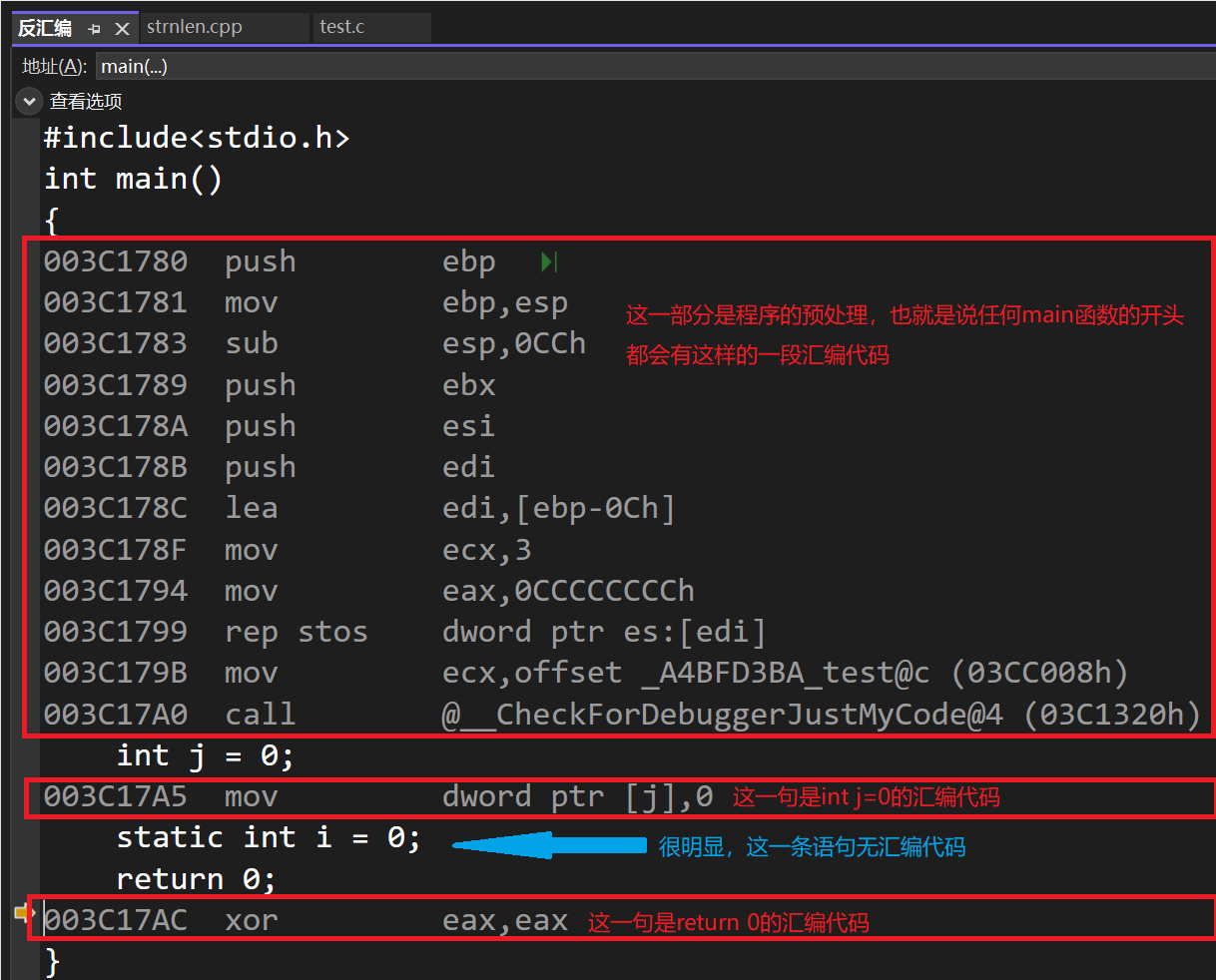
C语言:static关键字的使用
1.static修饰局部变量 这是static关键字使用最多的情况。我们知道局部变量是在程序运行阶段在栈上创建的,但是static修饰的局部变量是在程序编译阶段在代码段(静态区)创建的。所以在static修饰的变量所在函数执行结束后该变量依然存在。 //…...
:ECUM的ISOLAR-AB配置及代码解析)
AUTOSAR知识点 之 ECUM (三):ECUM的ISOLAR-AB配置及代码解析
目录 1、概述 2、ISOLAR-AB配置 2.1、EcuMGeneral 2.2、EcuMConfiguration 2.2.1、EcuMDefaultShutdownTarget 2.2.2、EcuMDriverInitListOne...
2023年MySQL-8.0.34保姆级安装教程
重点放前面:演示环境为windows环境。 MySQL社区版本安装教程如下: 一、MySQL安装包下载二、安装配置设置三、配置环境变量 大体分为3个步骤:①安装包的下载;②安装配置设置;③配置环境变量 一、MySQL安装包下载 下载官…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
