数学建模--蒙特卡洛模型的Python实现
目录
1.算法思想简介
2.算法应用1:问题一阐述
3.算法应用1:问题一解决
4.算法应用2:问题二阐述
5.算法应用2:问题二解决
1.算法思想简介
#蒙特卡洛算法思想
"""
蒙特卡洛方法的理论其实很类似于概率论中一个比较重要的定理---大数定律。
其基本原理简单描述是先大量模拟,然后计算一个事件发生的次数,再通过这个发生次数除以总模拟次数,得到想要的结果。
这个时候我们在样本足够大的情况下我们认为这个事件发生的概率等于实验所得到的结果
"""2.算法应用1:问题一阐述
"""
Question1:
计算圆周率pi(Π)值
实验原理:
在正方形内部有一个相切的圆,圆面积/正方形面积之比是(PixRxR)/(2Rx2R)= Pi/4。
在这个正方形内随机产生n个点,假设点落在圆内的概率为P,那么P=圆面积/正方形面积,P= Pi/4。
如何计算点落在圆内的概率P?
可以计算点与中心点的距离,判断是否落在圆的内部,若这些点均匀分布,用M表示落到圆内投点数,N表示总的投点数,则圆周率Pi=4P=4xM/N。
"""3.算法应用1:问题一解决
#第一题求解代码
#我们假设r=1,a=0,b=0
import numpy as np
def Qustion1(n):r=1.0a=0b=0x_min=a-rx_max=a+ry_min=b-ry_max=b+rm=0#m是计算落在圆内的点的个数for i in range(n+1):x=np.random.uniform(x_min,x_max)y=np.random.uniform(y_min,y_max)if x*x+y*y<=1:m=m+1print("第一题的答案是:",4*(m/float(n)))
ans=Qustion1(1000000)
#cout:第一问题的答案是: 3.1414684.算法应用2:问题二阐述
""""
Question2:
计算函数定积分值:
实验原理:
若要求函数f(x)从a到b的定积分,我们可以用一个比较容易算得面积的矩型包围在函数的积分区间上(假设其面积为Area),
定积分值其实就是求曲线下方的面积。随机地向这个矩形框里面投点,统计落在函数f(x)下方的点数量占所有点数量的比例为P,
那么就可以据此估算出函数f(x)从a到b的定积分为Area*P。
此处我们将a和b设为0和1,函数f(x)=x^2。
"""5.算法应用2:问题二解决
#第二题求解代码
#此处我们将a和b设为0和1,函数f(x)=x^2。
def Question2(n):x_min=0y_min=0x_max=1y_max=1m=0for i in range(n+1):x=np.random.uniform(x_min,x_max)y=np.random.uniform(y_min,y_max)if y-x*x<0:m=m+1print("第二题的答案是:",m/float(n))
ans2=Question2(1000000)
#第二题的答案是: 0.334016相关文章:

数学建模--蒙特卡洛模型的Python实现
目录 1.算法思想简介 2.算法应用1:问题一阐述 3.算法应用1:问题一解决 4.算法应用2:问题二阐述 5.算法应用2:问题二解决 1.算法思想简介 #蒙特卡洛算法思想 """ 蒙特卡洛方法的理论其实很类似于概率论中一个比较重…...
MySQL访问和配置
目录 1.使用MySQL自带的客户端工具访问 2.使用DOS访问(命令行窗口WinR → cmd) 3.连接工具(SQLyog或其它) MySQL从小白到总裁完整教程目录:https://blog.csdn.net/weixin_67859959/article/details/129334507?spm1001.2014.3001.5502 1.使用MySQL自…...

note_前端框架Vue的安装和简单入门(Windows 11)
1. Vue安装 (1) 下载安装node.js和npm # 下载msi安装包 https://nodejs.org/en# 点击安装包,按提示安装 # 默认安装nodejs, npm, 在线文档; PATH配置# 确认安装是否成功,在dos中输入 node -v # 验证nodejs是否安装成功 npm -v # 验证nodejs包管…...

SILERGY(矽力杰)功率电子开关 SY6280AAC
SILERGY(矽力杰)功率电子开关 SY6280AAC Low Loss Power Distribution Switch SOT-5 Pacakge 2.4V ~ 5.5V (<6V) 0.6W Max. Current 2A Reverse blocking (no body diode) Programmable current limit ( Ilimits(A) 6800 / Rset(ohm). ) Application Circuit (Reco…...

mysql char 和varchar的区别?
char 和varchar的区别 1、 char 一定会使用指定的空间,varchar是根据数据来定空间 2、 char的插入数据效率理论上比varchar高:varchar是需要通过后面的记录数来计算 使用哪一种类型? 如果确定数据一定是占指定长度,那么使用char类…...

HttpClient默认重试机制
分析&回答 只有发生IOExecetion时才会发生重试InterruptedIOException、UnknownHostException、ConnectException、SSLException,发生这4中异常不重试get方法可以重试3次,post方法在socket对应的输出流没有被write并flush成功时可以重试3次。读/写超…...
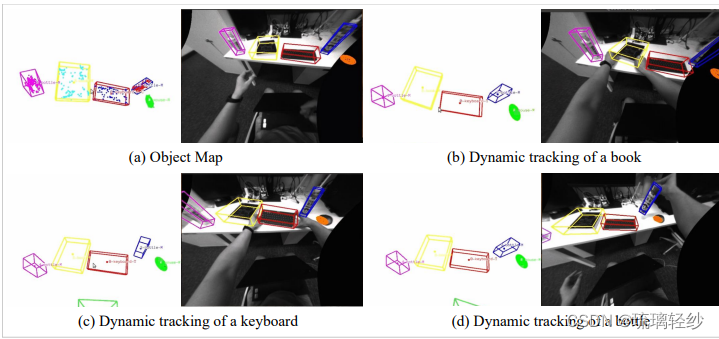
论文于祥读及复现——《Multi-level Map Construction for Dynamic Scenes》
论文祥读之——动态场景的多层次地图构建 0. 出发点(暨摘要)1. 引言2. 相关工作3.主要内容概括3.1 几何地图的构建3.1.1 密集点云地图和八叉图的构建3.1.2 平面地图的构建 3.2 对象地图的构建3.2.1 对象参数化和数据关联3.2.2 对象的更新与优化 4. 实验4…...
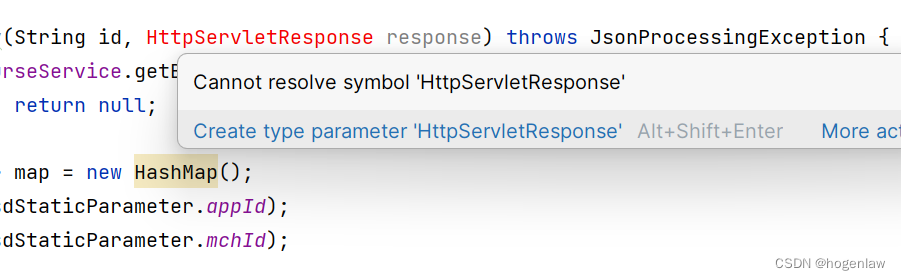
IDEA 报 Cannot resolve symbol ‘HttpServletResponse‘ 解决
springboot2版本换成springboot3之后,代码这里突然报红了, 首先要淡定,把原先Import的引入删掉,重新引入试试呢,是不是很简单哈哈。 原来,springboot3的路径是: import jakarta.servlet.http…...
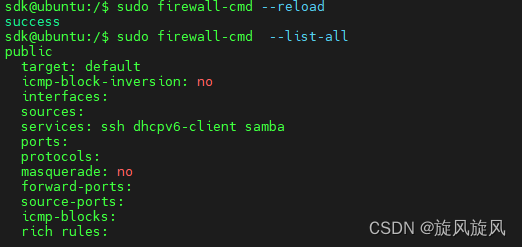
linux-samba-window登不上
登不上查了很久发现是防火墙导致的 sudo firewall-cmd --list-all //查看所有的防火墙信息sudo firewall-cmd --permanent --zonepublic --add-servicesamba //service里添加sambafirewall-cmd --reload //重启 便可以登录了,小问题...

Java Web3J :使用web3j监听、查询、订阅智能合约的事件
前面有文章写如何使用Docker-compose方式部署blockscout浏览器+charts图表,区块链浏览器已经部署成功了,同时我们在链上增加了治理投票流程,如何实时的把治理事件快速同步到浏览器呢?这时就想到了Web3J来监听智能合约的事件,来达到同步事件的效果 目录 Web3J简介功能简介m…...
C语言入门 Day_13 二维数组
目录 前言: 1.字符串 2.创建二维数组 3.使用二维数组 4.易错点 5.思维导图 前言: 我们学习了字符类型char,我们可以用char来表示一个大写或者小写的字母,但真实应用中我们往往使用的是多个字符组成的一个单词或者句子。 …...

通过HFS低成本搭建NAS,并内网穿透实现公网访问
文章目录 前言1.下载安装cpolar1.1 设置HFS访客1.2 虚拟文件系统 2. 使用cpolar建立一条内网穿透数据隧道2.1 保留隧道2.2 隧道名称2.3 成功使用cpolar创建二级子域名访问本地hfs 总结 前言 云存储作为一个新概念,在前些年炒的火热,虽然伴随一系列黑天鹅…...
【SpringMVC】工作流程及入门案例
目录 前言 回顾MVC三层架构 1. SpringMVC简介 …...
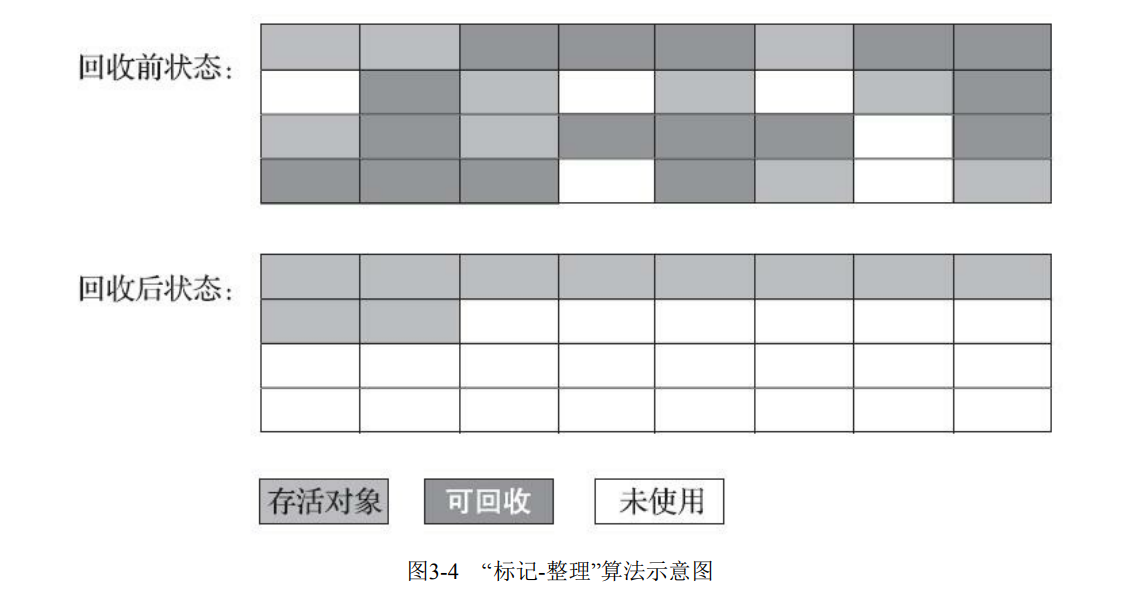
【JVM】垃圾收集算法
文章目录 分代收集理论标记-清除算法标记-复制算法标记-整理算法 分代收集理论 当前商业虚拟机的垃圾收集器,大多数都遵循了“分代收集”(Generational Collection)[1]的理论进 行设计,分代收集名为理论,实质是一套符…...
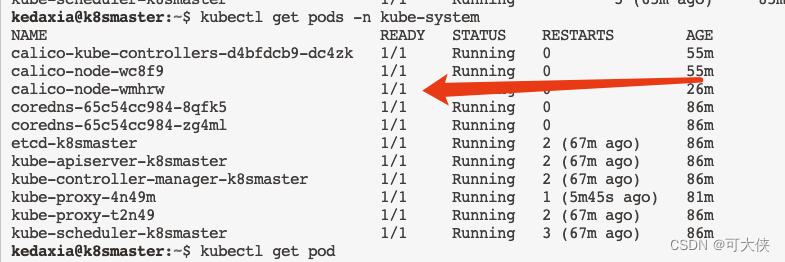
K8s的Pod出现Init:ImagePullBackOff问题的解决(以calico为例)
对于这类问题的解决思路应该都差不多,本文以calico插件安装为例,发现有个Pod的镜像没有pull成功 第一步:查看这个pod的描述信息 kubectl describe pod calico-node-wmhrw -n kube-system 从上图发现是docker拉取"calico/cni:v3.15.1&q…...
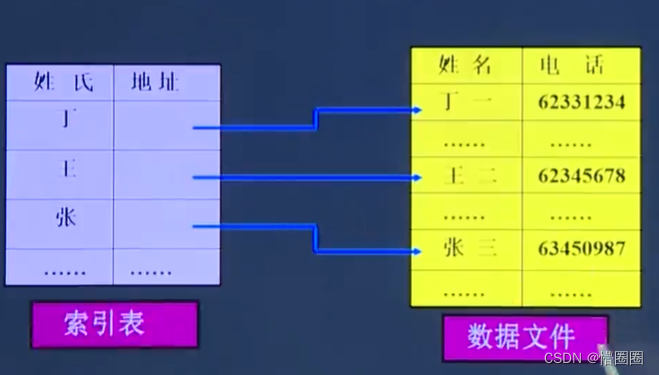
数据结构 -作用及基本概念
为什么要使用数据结构 学习数据结构是计算机科学和软件工程领域中非常重要的一门课程。以下是学习数据结构的几个重要原因: 组织和管理数据:数据结构提供了一种组织和管理数据的方式。通过学习不同的数据结构,你可以了解如何有效地存储和操作…...
数学建模--时间序列预测模型的七种经典算法的Python实现
目录 1.开篇版权提示 2.时间序列介绍 3.项目数据处理 4.项目数据划分可视化 5.时间预测序列经典算法1:朴素法 6.时间预测序列经典算法2: 简单平均法 7.时间预测序列经典算法3:移动平均法 8.时间预测序列经典算法4:简单指…...
nginx-反向代理缓存
反向代理缓存相当于自动化动静分离。 将上游服务器的资源缓存到nginx本地,当下次再有相同的资源请求时,直接讲nginx缓存的资源返回给客户端。 本地缓存资源有一个过期时间,当超过过期时间,则重新向上游服务器重新请求获取资源。…...

大模型重塑区域人才培养,飞桨(重庆)人工智能教育创新中心正式启动
2023年8月22日,重庆市高校人工智能产教融合院长研讨会暨飞桨(重庆)人工智能教育创新中心启动仪式在重庆大学成功召开。会上,由百度飞桨、重庆大学组织重庆市二十一所高校共建的飞桨(重庆)人工智能教育创新中…...

PAT 1164 Good in C 测试点3,4
个人学习记录,代码难免不尽人意。 When your interviewer asks you to write “Hello World” using C, can you do as the following figure shows? Input Specification: Each input file contains one test case. For each case, the first part gives the 26 …...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
