当前位置： 首页 > news >正文

如何在Win10系统上安装WSL（适用于 Linux 的 Windows 子系统）

news 2026/2/9 18:50:15

诸神缄默不语-个人CSDN博文目录

本文介绍的方法不是唯一的安装方案，但在我的系统上可用。

文章目录

  • 1. 视频版
  • 2. 文字版和代码
  • 3. 本文撰写过程中使用到的其他网络参考资料

1. 视频版

B站版：在Windows上安装Linux (WSL, 适用于 Linux 的 Windows 子系统)_哔哩哔哩_bilibili

2. 文字版和代码

  1. 用powershell安装Windows子系统支持：Enable-WindowsOptionalFeature -Online -FeatureName Microsoft-Windows-Subsystem-Linux
  2. 安装可用的Linux发行版（必须要在wsl --list --online的列表中的）
    在这里插入图片描述
  3. 打开虚拟机支持：控制面板-程序-启用或关闭Windows功能-虚拟机平台
  4. 在powershell中输入wsl进入环境

3. 本文撰写过程中使用到的其他网络参考资料

  1. 安装 WSL | Microsoft Learn
  2. 旧版 WSL 的手动安装步骤 | Microsoft Learn
  3. 打开Windows命令行、PowerShell窗口的多种方法
  4. [WSL]wsl.exe : 无法将“wsl.exe”项识别为 cmdlet、函数、脚本文件或可运行程序的名称
  5. windows功能启用和关闭-百度经验
  6. win10安装ubuntu系统，报错WslRegisterDistribution failed with error: 0x8007019e - bfhxt - 博客园
  7. win10内置ubuntu, “指定的网络名不再可用”解决办法_idjl的博客-CSDN博客

相关文章：

如何在Win10系统上安装WSL（适用于 Linux 的 Windows 子系统）

诸神缄默不语-个人CSDN博文目录 本文介绍的方法不是唯一的安装方案，但在我的系统上可用。 文章目录 1. 视频版2. 文字版和代码3. 本文撰写过程中使用到的其他网络参考资料 1. 视频版 B站版：在Windows上安装Linux (WSL, 适用于 Linux 的 Windows 子系统…...

编程日记 2023/9/5 8:39:50

单片机通用学习-​什么是寄存器？​

什么是寄存器？ 寄存器是一种特殊的存储器，主要用于存储和检查微机的状态。CPU寄存器用于存储和检查CPU的状态，具体包括计算中途数据、程序因中断或子程序分支时的返回地址、计算结果为零时的负值、计算结果为零时的信息、进位值等。 由于CP…...

编程日记 2023/9/5 8:38:49

【C语言】文件操作详解

文章目录 前言一、文件是什么二、文件具体介绍1.文件名2.文件类型3.文件缓冲区4.文件指针5.文件的打开和关闭 三、文件的顺序读写1.字符输入函数（fgetc）2.字符输出函数（fputc）3.文本行输入函数（fgets）4.文本…...

编程日记 2023/9/5 8:37:48

栈（Stack）的详解

目录 1.栈的概念 2.栈的模拟实现 1.栈的方法 2.模拟栈用（整型）数组的形式呈现 2.1栈的创建 2.2压栈 2.3栈是否为空 2.4出栈 2.5获取栈中有效元素个数 2.6获取栈顶元素 2.7完整代码实现 1.栈的概念 从上图中可以看到， Stack 继承了…...

编程日记 2023/9/5 8:36:46

深入了解GCC编译过程

关于Linux的编译过程，其实只需要使用gcc这个功能，gcc并非一个编译器，是一个驱动程序。其编译过程也很熟悉：预处理–编译–汇编–链接。在接触底层开发甚至操作系统开发时，我们都需要了解这么一个知识点，如何…...

编程日记 2023/9/5 8:35:44

leetcode 594.最长和谐子序列（滑动窗口）

⭐️ 题目描述 🌟 leetcode链接：最长和谐子序列 思路： 第一步先将数组排序，在使用滑动窗口（同向双指针），定义 left right 下标，比如这一组数 {1,3,2,2,5,2,3,7} 排序后 {1,2,2,2,3,…...

编程日记 2023/9/5 8:34:44

深入剖析云计算与云服务器ECS：从基础到实践

云计算已经在不断改变着我们的计算方式和业务模式，而云服务器ECS（Elastic Compute Service）作为云计算的核心组件之一，为我们提供了灵活、可扩展的计算资源。在本篇长文中，我们将从基础开始，深入探讨云计算…...

编程日记 2023/9/5 8:33:40

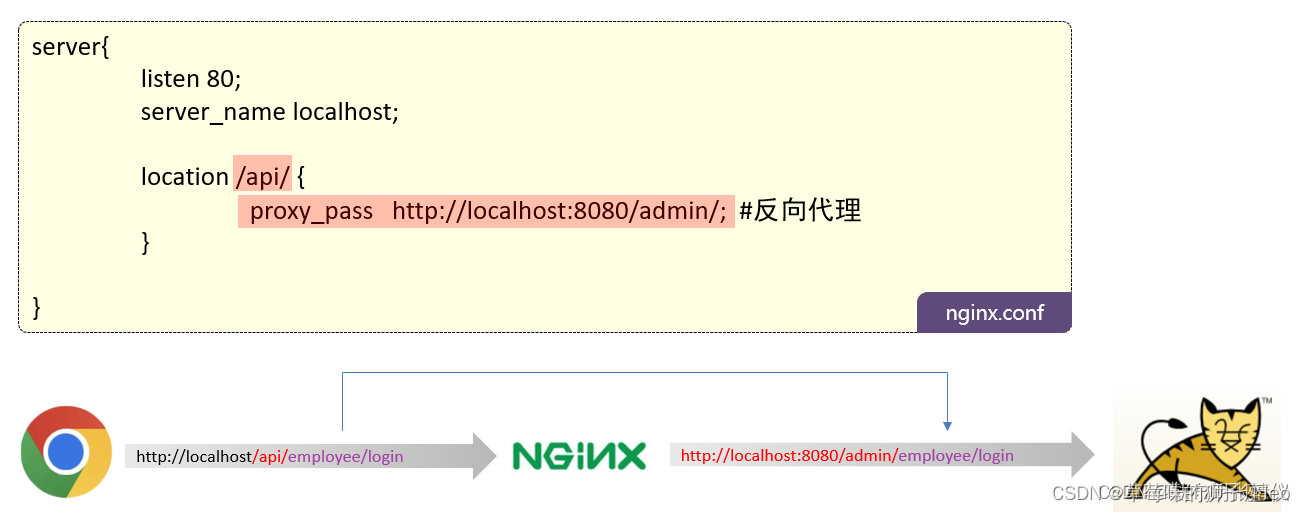
苍穹外卖技术栈

重难点详解 1、定义全局异常 2、ThreadLocal ThreadLocal 并不是一个Thread，而是Thread的一个局部变量ThreadLocal 为每一个线程提供独立的存储空间，具有线程隔离的效果，只有在线程内才能取到值，线程外则不能访问 public void …...

编程日记 2023/9/5 8:32:38

重新开始 杂类：C++基础

目录 1.输入输出 2 . i 与 i 3.结构体 4.二进制 1.输入输出 #include<cstdio>//cin>>,cout #include<iostream>//printf,scanf &#xff08;1&#xff09; cin , cout输入输出流可直接用于数字&#xff0c;字符 &#xff08;2&#xff09;scanf(&quo…...

编程日记 2023/9/5 8:31:37

自用的markdown与latex特殊符号

\triangleq \approx \xlongequal[y\arctan x]{x\tan y} \sum_{\substack{j1 \\ j\neq i}} \iiint\limits_\Omega \overset{\circ}{\vec{r}} \varphi \checkmark \stackrel{\cdot\cdot\cdot}{x}≜ ≈ y arctan ⁡ x x tan ⁡ y ∑ j 1 j ≠ i ∭ Ω r ⃗ ∘ φ ✓ x ⋅ ⋅ ⋅…...

编程日记 2023/9/5 8:30:37

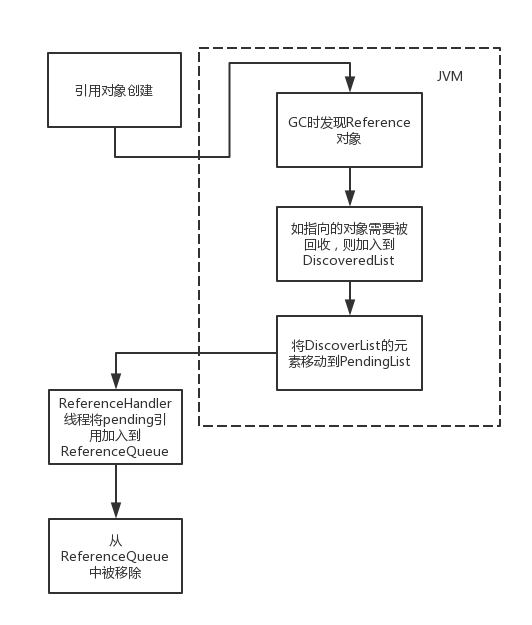
【20期】说一说Java引用类型原理

Java中一共有4种引用类型(其实还有一些其他的引用类型比如FinalReference)&#xff1a;强引用、软引用、弱引用、虚引用。 其中强引用就是我们经常使用的Object a new Object(); 这样的形式&#xff0c;在Java中并没有对应的Reference类。 本篇文章主要是分析软引用、弱引用、…...

编程日记 2023/9/5 8:29:36

无锡布里渊——厘米级分布式光纤-锅炉安全监测解决方案

无锡布里渊——厘米级分布式光纤-锅炉安全监测解决方案 厘米级分布式光纤-锅炉安全监测解决方案 1、方案背景与产品简介&#xff1a; 1.1&#xff1a;背景简介&#xff1a; 锅炉作为一种把煤、石油或天燃气等化石燃料所储藏的化学能转换成水或水蒸气的热能的重要设备&#xff…...

编程日记 2023/9/5 8:28:35

GREASELM: GRAPH REASONING ENHANCED LANGUAGE MODELS FOR QUESTION ANSWERING

本文是LLM系列文章&#xff0c;针对《GREASELM: GRAPH REASONING ENHANCED LANGUAGE MODELS FOR QUESTION ANSWERING》的翻译。 GREASELM&#xff1a;图推理增强的问答语言模型 摘要1 引言2 相关工作3 提出的方法&#xff1a;GREASELM4 实验设置5 实验结果6 结论 摘要 回答关…...

编程日记 2023/9/5 8:27:34

QT C++ 实现网络聊天室

一、基本原理及流程 1&#xff09;知识回顾&#xff08;C语言中的TCP流程&#xff09; 2&#xff09;QT中的服务器端/客户端的操作流程 二、代码实现 1&#xff09;服务器 .ui .pro 在pro文件中添加network库 .h #ifndef WIDGET_H #define WIDGET_H#include <QWidget>…...

编程日记 2023/9/5 8:26:32

每日一道面试题之什么是上下文切换？

上下文切换是指在计算机操作系统中&#xff0c;当多个进程或线程同时运行时&#xff0c;系统需要将当前运行进程或线程的状态&#xff08;包括程序计数器、寄存器值、内存映像等&#xff09;保存起来&#xff0c;然后切换到另一个进程或线程继续执行的过程。上下文切换通常由操…...

编程日记 2023/9/5 8:25:31

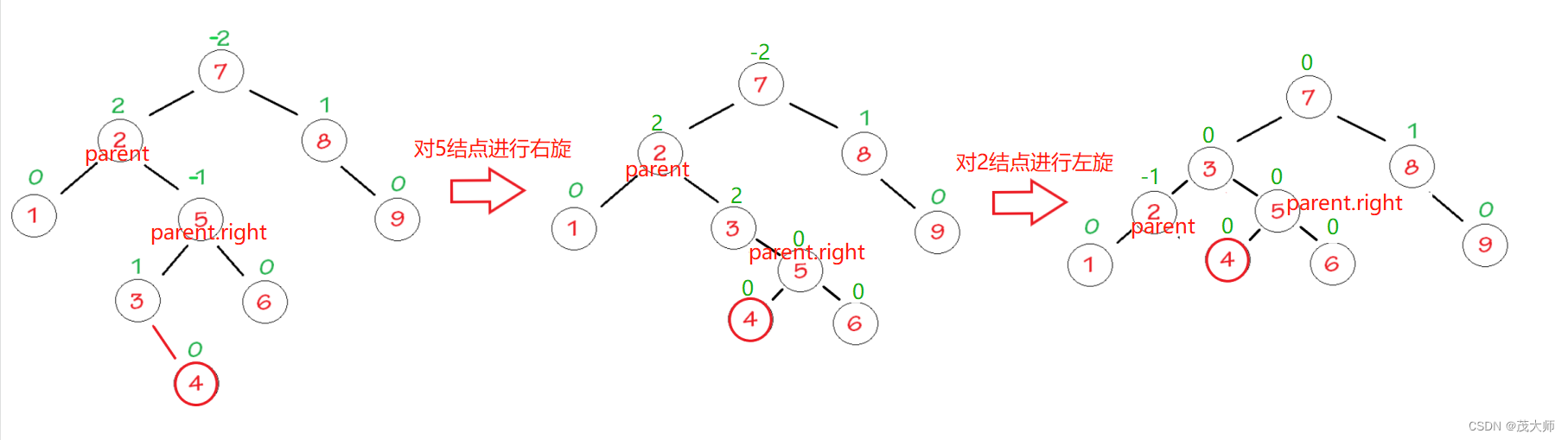
2023.9.3 关于 AVL 树

目录 二叉搜索树 二叉搜索树的简介&#xff1a; 二叉搜索树的查找&#xff1a; 二叉搜索树的效率&#xff1a; AVL树 AVL 树的简介&#xff1a; AVL 树的实现&#xff1a; AVL树的旋转 右单旋 左单旋 左右双旋 右左双旋 完整 AVL树插入代码 验证 AVL 树 AVL 树的性…...

编程日记 2023/9/5 8:24:30

机器学习课后习题 --- 机器学习实践

&#xff08;一&#xff09;单选题 1.以下关于训练集、验证集和测试集说法不正确的是( )。 A:测试集是纯粹是用于测试模型泛化能力B:训练集是用来训练以及评估模型性能 C:验证集用于调整模型参数 D:以上说法都不对 2.当数据分布不平衡时&#xff0c;我们可采取的措施不包括…...

编程日记 2023/9/5 8:23:28

git常用操作

删除分支 例&#xff1a;例如想删除的分支是dev_delete,那么可以按照如下的操作进行 #查看当前所在分支 git branch#如果在当前dev_delete分支上&#xff0c;就要切换到其他分支才能删除该分支 git checkout 其他分支#删除本地名为dev_delete的分支 git branch -d dev_delete…...

编程日记 2023/9/5 8:22:27

QT的补充知识

一、文件 QFile QT提供了QFile类用于对文件进行读写操作&#xff0c;也提供了其他的两个类&#xff1a;文本流&#xff08;QTextSream&#xff09;和数据流&#xff08;QDataStream&#xff09; 文本流&#xff08;QTextSream&#xff09;&#xff1a;用于对文本数据的处理&am…...

编程日记 2023/9/5 8:21:25

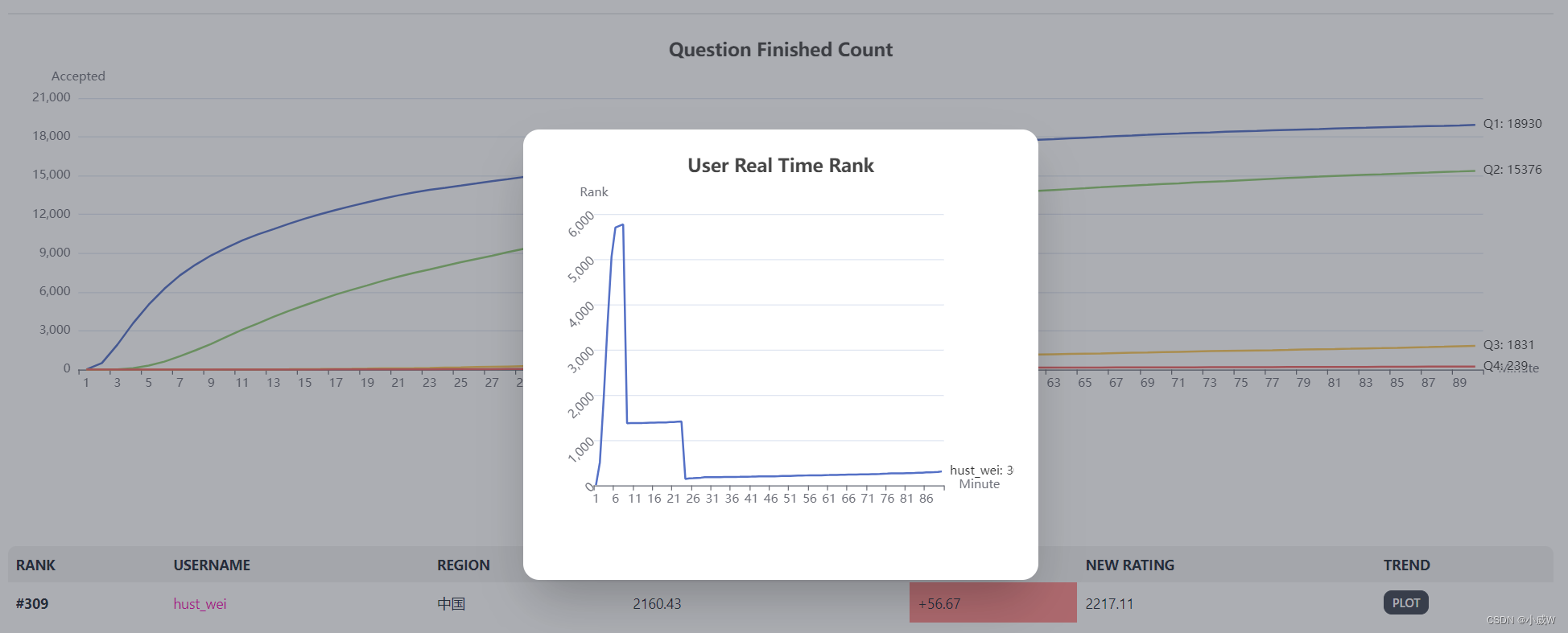
【力扣周赛】第 360 场周赛（贪心 ⭐树上倍增）

文章目录 竞赛链接Q1&#xff1a;8015. 距离原点最远的点&#xff08;贪心&#xff09;Q2&#xff1a;8022. 找出美丽数组的最小和&#xff08;贪心&#xff09;Q3&#xff1a;2835. 使子序列的和等于目标的最少操作次数&#xff08;贪心&#xff09;思路竞赛时丑陋代码&#x…...

编程日记 2023/9/5 8:20:24

工业安全零事故的智能守护者：一体化AI智能安防平台

前言&#xff1a; 通过AI视觉技术&#xff0c;为船厂提供全面的安全监控解决方案&#xff0c;涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面&#xff0c;能够实现对应负责人反馈机制&#xff0c;并最终实现数据的统计报表。提升船厂…...

编程新知 2026/1/21 9:20:07

shell脚本--常见案例

1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件&#xff1a; 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

编程新知 2026/2/7 19:53:11

基于服务器使用 apt 安装、配置 Nginx

&#x1f9fe; 一、查看可安装的 Nginx 版本 首先&#xff0c;你可以运行以下命令查看可用版本&#xff1a; apt-cache madison nginx-core输出示例&#xff1a; nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

编程新知 2026/1/9 12:53:59

【第二十一章 SDIO接口(SDIO)】

第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

编程新知 2026/2/1 13:28:03

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法（ISWC2024）

笔记整理&#xff1a;刘治强&#xff0c;浙江大学硕士生&#xff0c;研究方向为知识图谱表示学习&#xff0c;大语言模型 论文链接&#xff1a;http://arxiv.org/abs/2407.16127 发表会议&#xff1a;ISWC 2024 1. 动机 传统的知识图谱补全&#xff08;KGC&#xff09;模型通过…...

编程新知 2026/1/31 12:03:23

Python爬虫（一）：爬虫伪装

一、网站防爬机制概述 在当今互联网环境中&#xff0c;具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类&#xff1a; 身份验证机制&#xff1a;直接将未经授权的爬虫阻挡在外反爬技术体系&#xff1a;通过各种技术手段增加爬虫获取数据的难度…...

编程新知 2026/1/30 20:42:46

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理）

上一章用到了V2 的概念&#xff0c;其实 Fiori当中还有 V4&#xff0c;咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务)&#xff0c;代理中间件&#xff08;ui5-middleware-simpleproxy&#xff09;-CSDN博客…...

编程新知 2026/2/3 8:20:06

MySQL 知识小结（一）

一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库&#xff0c;分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷&#xff0c;但是文件存放起来数据比较冗余&#xff0c;用二进制能够更好管理咱们M…...

编程新知 2026/1/26 13:29:47

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

解读《网络安全法》最新修订，把握网络安全新趋势

《网络安全法》自2017年施行以来&#xff0c;在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂&#xff0c;网络攻击、数据泄露等事件频发&#xff0c;现行法律已难以完全适应新的风险挑战。 2025年3月28日&#xff0c;国家网信办会同相关部门起草了《网络安全…...

编程新知 2026/1/31 4:40:38