基础算法(一)
目录
一.排序
快速排序:
归并排序:
二.二分法
整数二分模板:
浮点二分:
一.排序
快速排序:
- 从数列中挑出一个元素,称为 "基准"
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区操作。
- 递归把小于基准值元素的子数列和大于基准值元素的子数列排序。
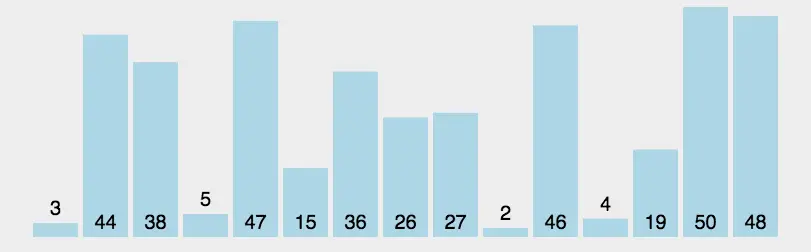
static void quick_sort(int[] arr,int l,int r){if (l>=r) return;//特判小于等于1个的数组int x=arr[(l+r)>>1],i=l-1,j=r+1;//取分隔基准while (i<j){//把小于x的数放左边,大于x的数放右边//跳过已符合条件do i++; while (arr[i]<x);do j--; while (arr[j]>x);//交换使符合条件if (i<j){int t=arr[i];arr[i]=arr[j];arr[j]=t;}}//递归左右边排序quick_sort(arr,l,j);quick_sort(arr,j+1,r);}归并排序:
利用归并(先递归排序子元素,再合并)的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。

static void merge_sort(int[] arr, int l, int r) {if (l >= r) return;int mid = l + r >> 1;merge_sort(arr, l, mid);//递归排序左merge_sort(arr, mid + 1, r);//右//合并int[] tmp = new int[arr.length];int k = 0, i = l, j = mid + 1;while (i <= mid && j <= r) {//从排序好的左右数组取最小依次放入tmp数组,知道某一个数组取完if (arr[i] < arr[j])tmp[k++] = arr[i++];elsetmp[k++] = arr[j++];}//剩余部分直接放入tmp数组末尾while (i <= mid) tmp[k++] = arr[i++];while (j <= r) tmp[k++] = arr[j++];//tmp数组赋给原数组for (i = l, j = 0; i <= r; i++, j++) arr[i] = tmp[j];}二.二分法
二分法的思想很简单,因为整个数组是单调的,每次判断后可将另外一半直接排除,大大提高查找效率,但是二分查找的边界问题很容易成为问题
整数二分模板:
static int binary_search1(int[] arr,int l, int r){while (l<r){int mid=l+r>>1;if (check(mid)){r=mid;}else {l=mid+1;}}return l;}static int binary_search2(int[] arr,int l,int r){while (l<r){int mid=l+r+1>>1;if(check(mid)){l=mid;}else {r=mid-1;}}return l;}根据具体情况选择判断后边界的取值,特别注意不同边界下mid的初始化.
浮点二分:
static double binary_search3(double[] arr,double l,double r){final double eps=1e-6;while (r-l>eps){double mid=(l+r)/2;if (check(mid)) r=mid;else l=mid;}return l;}浮点二分的核心在使用eps的精度进行判断
相关文章:

基础算法(一)
目录 一.排序 快速排序: 归并排序: 二.二分法 整数二分模板: 浮点二分: 一.排序 快速排序: 从数列中挑出一个元素,称为 "基准"重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面&#…...
Consider defining a bean of type问题解决
Consider defining a bean of type问题解决 Consider defining a bean of type问题解决 包之后,发现项目直接报错Consider defining a bean of type。 会有一些包你明明Autowired 但是还是找不到什么bean 导致你项目启动不了 解决方法一: 这个问题主要是因为项目拆包…...

Android 1.2.1 使用Eclipse + ADT + SDK开发Android APP
1.2.1 使用Eclipse ADT SDK开发Android APP 1.前言 这里我们有两条路可以选,直接使用封装好的用于开发Android的ADT Bundle,或者自己进行配置 因为谷歌已经放弃了ADT的更新,官网上也取消的下载链接,这里提供谷歌放弃更新前最新…...
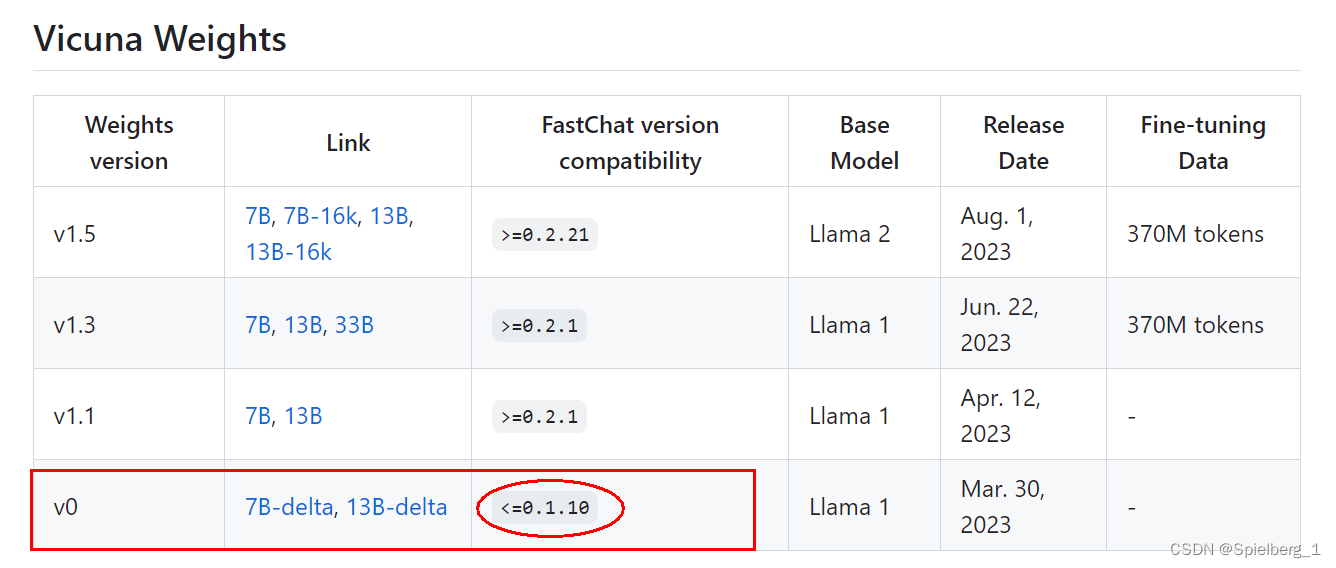
Llama-7b-hf和vicuna-7b-delta-v0合并成vicuna-7b-v0
最近使用pandagpt需要vicuna-7b-v0,重新过了一遍,前段时间部署了vicuna-7b-v3,还是有不少差别的,transforms和fastchat版本更新导致许多地方不匹配,出现很多错误,记录一下。 更多相关内容可见Fastchat实战…...

Centos、OpenEuler系统安装mysql
要在CentOS上安装MySQL并设置开机自启和root密码,请按照以下步骤进行操作: 确保您的CentOS系统已连接到Internet,并且具有管理员权限(root或sudo访问权限)。打开终端或SSH会话,使用以下命令安装MySQL&…...
如何在Win10系统上安装WSL(适用于 Linux 的 Windows 子系统)
诸神缄默不语-个人CSDN博文目录 本文介绍的方法不是唯一的安装方案,但在我的系统上可用。 文章目录 1. 视频版2. 文字版和代码3. 本文撰写过程中使用到的其他网络参考资料 1. 视频版 B站版:在Windows上安装Linux (WSL, 适用于 Linux 的 Windows 子系统…...
单片机通用学习-什么是寄存器?
什么是寄存器? 寄存器是一种特殊的存储器,主要用于存储和检查微机的状态。CPU寄存器用于存储和检查CPU的状态,具体包括计算中途数据、程序因中断或子程序分支时的返回地址、计算结果为零时的负值、计算结果为零时的信息、进位值等。 由于CP…...

【C语言】文件操作详解
文章目录 前言一、文件是什么二、文件具体介绍1.文件名2.文件类型3.文件缓冲区4.文件指针5.文件的打开和关闭 三、文件的顺序读写1.字符输入函数(fgetc)2.字符输出函数(fputc)3.文本行输入函数(fgets)4.文本…...

栈(Stack)的详解
目录 1.栈的概念 2.栈的模拟实现 1.栈的方法 2.模拟栈用(整型)数组的形式呈现 2.1栈的创建 2.2压栈 2.3栈是否为空 2.4出栈 2.5获取栈中有效元素个数 2.6获取栈顶元素 2.7完整代码实现 1.栈的概念 从上图中可以看到, Stack 继承了…...

深入了解GCC编译过程
关于Linux的编译过程,其实只需要使用gcc这个功能,gcc并非一个编译器,是一个驱动程序。其编译过程也很熟悉:预处理–编译–汇编–链接。在接触底层开发甚至操作系统开发时,我们都需要了解这么一个知识点,如何…...

leetcode 594.最长和谐子序列(滑动窗口)
⭐️ 题目描述 🌟 leetcode链接:最长和谐子序列 思路: 第一步先将数组排序,在使用滑动窗口(同向双指针),定义 left right 下标,比如这一组数 {1,3,2,2,5,2,3,7} 排序后 {1,2,2,2,3,…...

深入剖析云计算与云服务器ECS:从基础到实践
云计算已经在不断改变着我们的计算方式和业务模式,而云服务器ECS(Elastic Compute Service)作为云计算的核心组件之一,为我们提供了灵活、可扩展的计算资源。在本篇长文中,我们将从基础开始,深入探讨云计算…...
苍穹外卖技术栈
重难点详解 1、定义全局异常 2、ThreadLocal ThreadLocal 并不是一个Thread,而是Thread的一个局部变量ThreadLocal 为每一个线程提供独立的存储空间,具有线程隔离的效果,只有在线程内才能取到值,线程外则不能访问 public void …...

重新开始 杂类:C++基础
目录 1.输入输出 2 . i 与 i 3.结构体 4.二进制 1.输入输出 #include<cstdio>//cin>>,cout #include<iostream>//printf,scanf (1) cin , cout输入输出流可直接用于数字,字符 (2)scanf(&quo…...

自用的markdown与latex特殊符号
\triangleq \approx \xlongequal[y\arctan x]{x\tan y} \sum_{\substack{j1 \\ j\neq i}} \iiint\limits_\Omega \overset{\circ}{\vec{r}} \varphi \checkmark \stackrel{\cdot\cdot\cdot}{x}≜ ≈ y arctan x x tan y ∑ j 1 j ≠ i ∭ Ω r ⃗ ∘ φ ✓ x ⋅ ⋅ ⋅…...
【20期】说一说Java引用类型原理
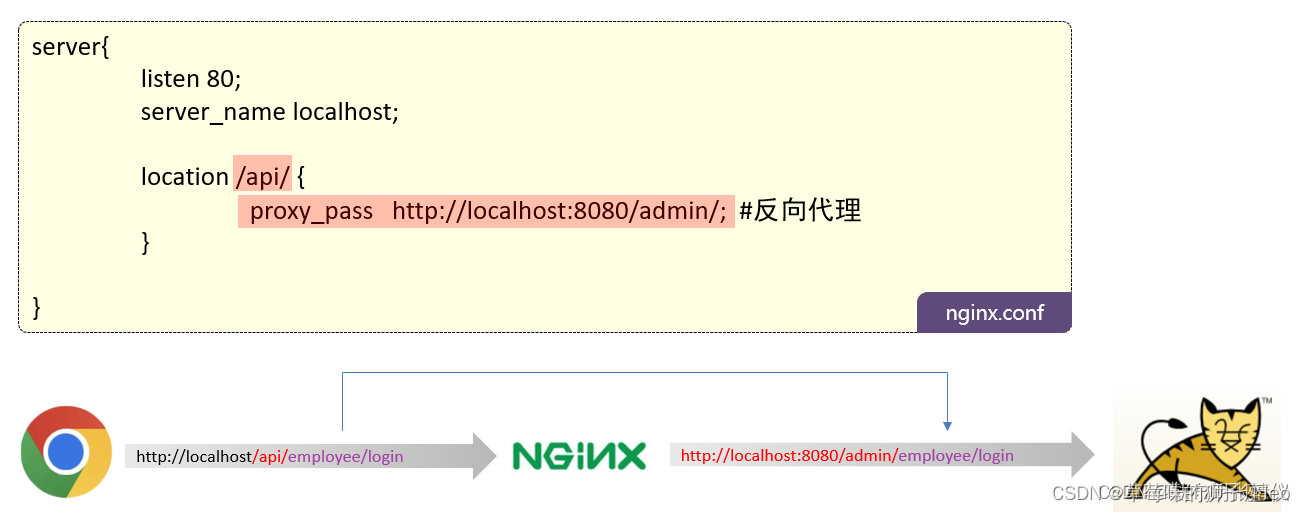
Java中一共有4种引用类型(其实还有一些其他的引用类型比如FinalReference):强引用、软引用、弱引用、虚引用。 其中强引用就是我们经常使用的Object a new Object(); 这样的形式,在Java中并没有对应的Reference类。 本篇文章主要是分析软引用、弱引用、…...

无锡布里渊——厘米级分布式光纤-锅炉安全监测解决方案
无锡布里渊——厘米级分布式光纤-锅炉安全监测解决方案 厘米级分布式光纤-锅炉安全监测解决方案 1、方案背景与产品简介: 1.1:背景简介: 锅炉作为一种把煤、石油或天燃气等化石燃料所储藏的化学能转换成水或水蒸气的热能的重要设备ÿ…...

GREASELM: GRAPH REASONING ENHANCED LANGUAGE MODELS FOR QUESTION ANSWERING
本文是LLM系列文章,针对《GREASELM: GRAPH REASONING ENHANCED LANGUAGE MODELS FOR QUESTION ANSWERING》的翻译。 GREASELM:图推理增强的问答语言模型 摘要1 引言2 相关工作3 提出的方法:GREASELM4 实验设置5 实验结果6 结论 摘要 回答关…...
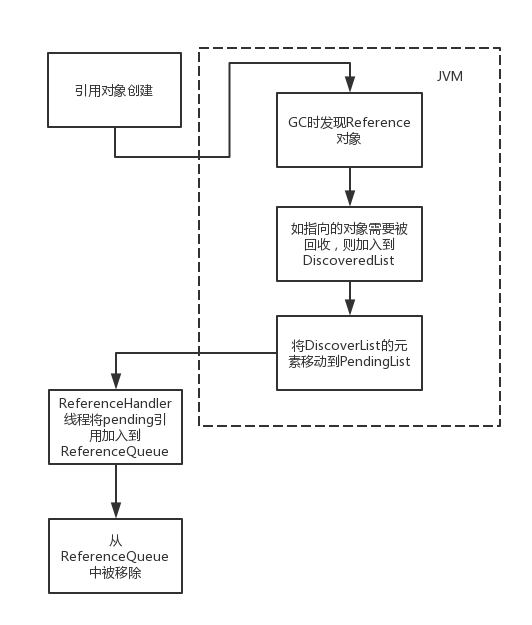
QT C++ 实现网络聊天室
一、基本原理及流程 1)知识回顾(C语言中的TCP流程) 2)QT中的服务器端/客户端的操作流程 二、代码实现 1)服务器 .ui .pro 在pro文件中添加network库 .h #ifndef WIDGET_H #define WIDGET_H#include <QWidget>…...

每日一道面试题之什么是上下文切换?
上下文切换是指在计算机操作系统中,当多个进程或线程同时运行时,系统需要将当前运行进程或线程的状态(包括程序计数器、寄存器值、内存映像等)保存起来,然后切换到另一个进程或线程继续执行的过程。上下文切换通常由操…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...
