有序表之红黑树
文章目录
- 1、五个条件
- 2、调整策略
- 2.1 插入调整的情况
- 2.1.1 情况一:插入节点是红色,其父节点也是红色
- 2.1.2 情况二
- 2.1.2 代码实现
- 2.2 删除调整的情况
- 2.2.1 情况一:双重黑节点的兄弟节点也是黑色,且其兄弟的两个孩子也是黑色
- 2.2.2 情况二:双重黑节点的兄弟节点是黑色,兄弟节点存在红色的子节点
- 2.2.3 情况三
- 2.2.4 思考:双黑节点的兄弟节点如果是红色,怎么办
- 2.2.5 代码实现
- 3、总结
- 3.1 平衡条件
- 3.2 学习诀窍
- 3.3 插入策略
- 3.4 插入调整代码重点
- 3.5 删除调整发生的前提
- 3.6 删除调整
- 3.7 删除调整代码重点
1、五个条件
- 每个节点非黑即红
- 根节点是黑色
- 叶节点(NIL)是黑色【虚拟空节点,并不是看得见的叶子节点】
- 如果一个节点是红色,则它的两个子节点都是黑色的
- 从根节点出发到所有叶节点的路径上,黑色节点数量相同
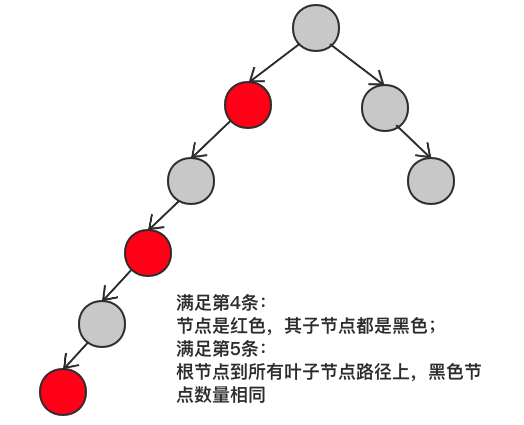
结合第4点和第5点,红黑树中最短的路径和最长的路径之间的关系是:最长路径 = 2 x 最短路径。
假设最短边有3个黑色节点,那么最长边就是黑红相间的节点(不包含NIL节点):
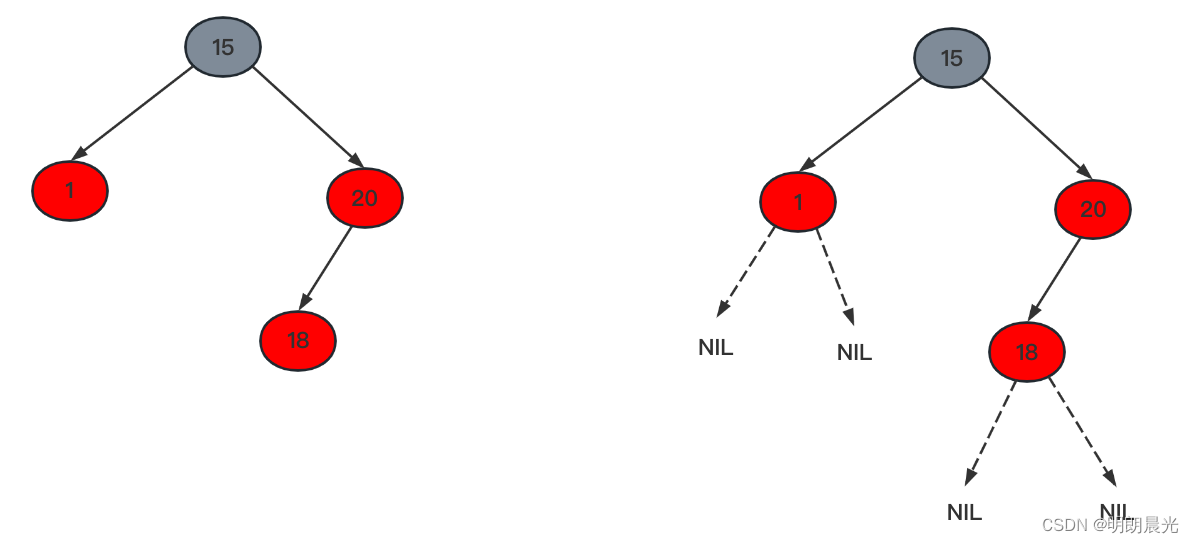
如下左图所示的不是红黑树,因为其红色节点的子节点不是且黑色叶子节点不是黑色 ,而叶子节点并不是指的图中的1和18,而是右图所示的没有画出来的NIL结点:
可见,红黑树的本质也是用树高控制平衡:最长路径 = 2 x 最短路径,但是相比AVL数控制得更松散一些,目的是不经常调整,减轻内存IO的消耗。
2、调整策略
- 插入调整站在 祖父节点 看
- 删除调整站在 父节点 看
- 插入和删除的情况处理一共 5 种
2.1 插入调整的情况
【分析】
如果插入的节点是黑色的,那么就有一条路径上黑色节点的数量发生了改变,这个时候就需要进行调整。所以如果插入结点是黑色的,必然会调整。(即 插入黑色节点必然会调整)
而插入红色节点,不会影响黑色节点的数量,如果红色节点插入到黑色节点下则不需要调整,如果插入到红色节点下,才需要调整。所以,插入红色节点可能会调整。(即 红色节点可能会调整)
所以,红黑树在插入一个节点的时候,插入的节点必然是红色。
2.1.1 情况一:插入节点是红色,其父节点也是红色
xxx 为新插入的节点
1)在插入操作回溯过程中,回溯到20节点发现冲突了,但是不要管它,继续往上回溯;回溯到15(祖父节点),向下看的时候发现20和18冲突,这个时候才进行调整。
2)将上图的这棵树看作一棵大的红黑树的子树。这部分 调整之前每条路径上的黑色节点数量 等于 调整之后每条路径上的黑色节点数量。即上图的这棵树,调整之前,每条路径上只有1个黑色节点,那么调整之后每条路径上也是1个黑色节点。之所以这么要求,就是为了不对红黑树的其他部分产生影响。这是一个通用的调整策略。【就算把15当做根节点,调整之后它是红色,那么最后一检查发现根节点不是黑色,将它变成黑色就行了】
3)当前(15, 1, 20)构成了 “黑-红-红” 的结构,这个“小帽子”,会给下面的子树每条路径提供一个黑色节点;但是还有一种红-黑-黑“小帽子”的情况,也会给子树每条路径提供一个黑色节点。这两种情况是等价的。(如下图所示的两种“小帽子”)
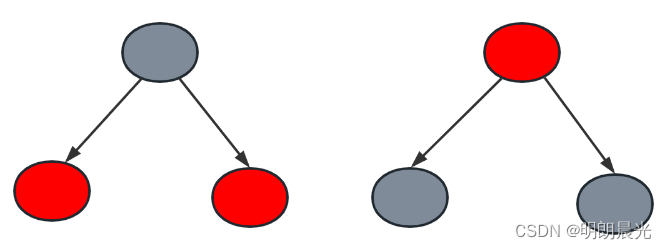
因此,情况一的调整方式:从祖父节点(黑色)向下看,两个子节点都是红色,并且孙子节点也有红色的时候,就将祖父节点改成红色,将它的两个孩子染成黑色(红-黑-黑)。
注意:之所以要将这棵树看作一棵大的红黑树的子树,是因为即便 15 变成了红色,就算它和它的父节点发生了冲突也是不处理的,而是要一直回溯到它的祖父节点才进行处理,这个过程是动态的。
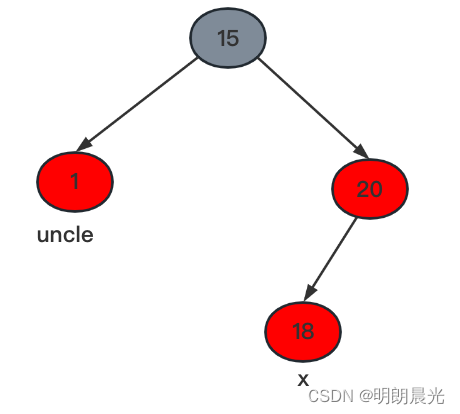
针对该样例的处理办法:1 和 20 修改成黑色,15 修改为红色(所谓红色上顶)。
情况一包含了 4 种小情况:插入的 xxx 是 1 的左节点或右节点、是 20 的左节点或右节点。
2.1.2 情况二
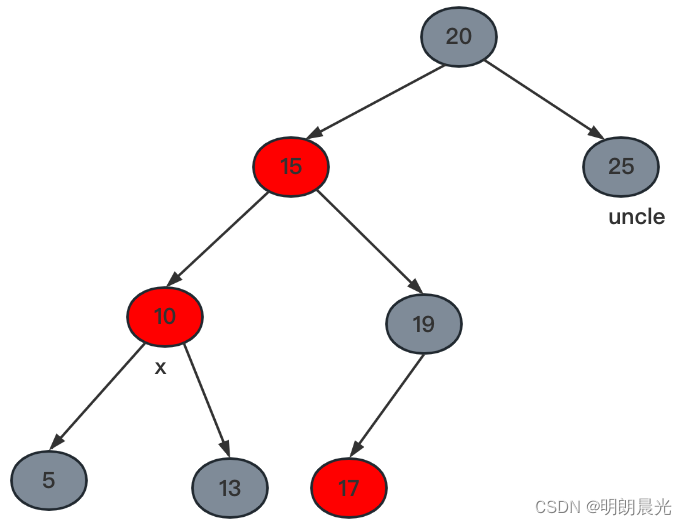
这种情况就是:祖父节点来看,它的左孩子是红色,左孩子的左孩子也是红色,但是右孩子为黑色。
从祖父节点(20)来看,它的左孩子是红色,左孩子的左孩子也是红色,就类似于AVL树中的LL类型失衡。
当发生LL失衡的时候,可以确定[20, 15, 10, 5, 13, 19, 25]都是确定的点以及就是图中的颜色,而17这个节点的颜色是不确定的。【将10号节点想象为(10,5,13)调整完后变成了红色,不然不好理解插入10不平衡的情况下它还有子节点】
抓着失衡节点20进行右旋得到如图:
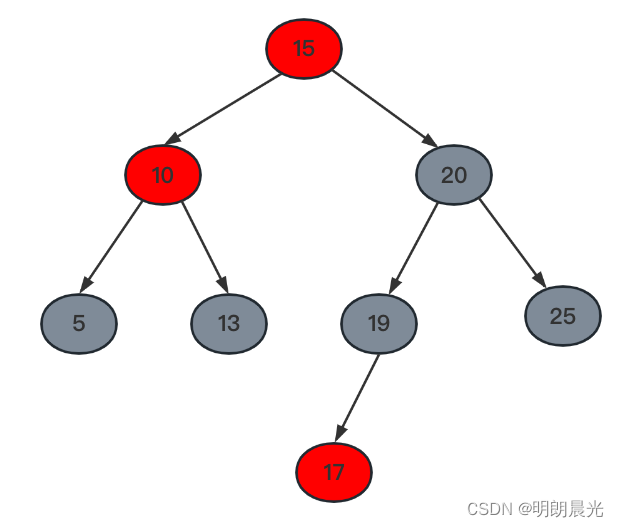
红黑树的调整原则:调整前每条路径上的黑色节点数量 = 调整后每条路径上的黑色节点数量
调整前,每条路径上的黑色节点数量为 2 个,则调整后每条路径上的黑色节点数量也是 2 个。而现在右旋后 [5, 13, 19, 25] 都是确定的黑色,也就是说需要在[15, 10, 20] 这个”小帽子“ 中再提供一个黑色节点,即是将当前的"小帽子"改成要么是 黑-红-红,要么是 红-黑-黑。
根节点改成红色叫做红色上浮(红-黑-黑),改成黑色叫做红色下沉(黑-红-红)。
总结来说,对于情况二,即LL类型失衡有两种调整策略:
① 先进行大右旋,然后将 “小帽子” 改成 黑-红-红 的结构;
② 先进行大右旋,然后将 “小帽子” 改成 红-黑-黑 的结构;
针对给出的样例,其中一种处理办法:大右(左)旋,20 调整成红色,15 调整成黑色,即可搞定问题。
对于LR类型失衡:先进行小左旋,转换为LL类型失衡,然后进行大右旋,最后调整颜色。(注:在小左旋的时候并不会改变子树上黑色节点数量的改变)
基于AVL中的平衡调整,RR类型失衡和RL类型失衡也可以类似进行处理。
2.1.2 代码实现
#include <stdio.h>
#include <stdlib.h>//只包含红黑树的insert操作typedef struct Node {int key;int color;//0 red, 1 black, 2 double blackstruct Node *lchild, *rchild;
} Node;Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void init_NIL() {NIL->key = 0;NIL->color = 1;NIL->lchild = NIL->rchild = NIL;return ;
}
//节点初始化
Node *getNewNode(int key) {Node *p = (Node *)malloc(sizeof(Node));p->key = key;p->color = 0;p->lchild = p->rchild = NIL;return p;
}int has_red_child(Node *root) {return root->lchild->color == 0 || root->rchild->color == 0;
}Node *left_rotate(Node *root) {Node *temp = root->rchild;root->rchild = temp->lchild;temp->lchild = root;return temp;
}Node *right_rotate(Node *root) {Node *temp = root->lchild;root->lchild = temp->rchild;temp->rchild = root;return temp;
}Node *insert_maintain(Node *root) {//当前节点没有红色子孩子,不会发生冲突,不需要做任何调整if (!has_red_child(root)) return root;//判断双红的情况:冲突发生在哪棵子树int flag = 0;//如果左右孩子都为红色,直接修改为红黑黑。处理插入情况1。//即便不发生冲突,这样修改也没有影响//这是一种偷懒的做法,因为没有判断是否发生了冲突if (root->lchild->color == 0 && root->rchild->color == 0) {//root->color = 0;//root->lchild->color = root->rchild->color = 1;//return root;goto insert_end;}//左孩子为红色,且左孩子的左孩子/右孩子也是红色(左子树发生了冲突)if (root->lchild->color == 0 && has_red_child(root->lchild)) flag = 1;//右孩子为红色,且右孩子的左孩子/右孩子也是红色(右子树发生了冲突)if (root->rchild->color == 0 && has_red_child(root->rchild)) flag = 2;//flag = 0表示没有发生冲突if (flag == 0) return root;if (flag == 1) {//L开头的失衡//判断是否为LR型,LR型需要先小左旋if (root->lchild->rchild->color == 0) {root->lchild = left_rotate(root->lchild);}root = right_rotate(root);} else { //R开头的失衡if (root->rchild->lchild->color == 0) {root->rchild = right_rotate(root->rchild);}root = left_rotate(root);}
insert_end://修改三元组小帽子的颜色(可以红色上浮或红色下沉的改法)//此处使用的是红色上浮的改法:红-黑-黑root->color = 0;root->lchild->color = root->rchild->color = 1;return root;
}//插入操作
Node *__insert(Node *root, int key) {if (root == NIL) return getNewNode(key);if (root->key == key) return root;if (key < root->key) {root->lchild = __insert(root->lchild, key);} else {root->rchild = __insert(root->rchild, key);}//回溯过程中进行插入调整return insert_maintain(root);
}//给根节点染头为黑色,修改根节点的颜色为黑色,这是真正的根节点,如果是由红色变成黑色会给每条路径都增加一个黑色节点
//此处是调整解决冲突后的整棵树的根
Node *insert(Node *root, int key) {root = __insert(root, key);root->color = 1;return root;
}//销毁操作
void clear(Node *root) {if (root == NIL) return ;clear(root->lchild);clear(root->rchild);free(root);return ;
}void print(Node *root) {printf("(%d| %d, %d %d)\n", root->color, root->key, root->lchild->key, root->rchild->key);return ;
}void output(Node *root) {if (root == NIL) return ;print(root);output(root->lchild);output(root->rchild);return ;
}int main() {int op, val;Node *root = NIL;while (~scanf("%d%d", &op, &val)) {switch (op) {case 1: root = insert(root, val); break;}output(root);printf("------------\n");}return 0;
}
运行测试:依次插入1,2,3
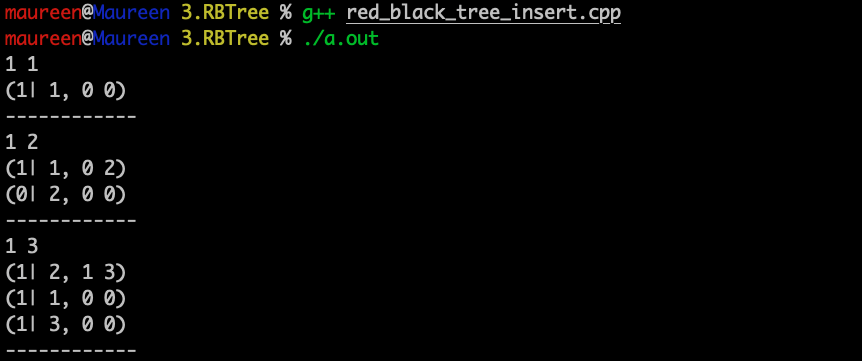
输出结果的意义:(根节点颜色| 根节点值,左孩子值,右孩子值)
结果说明:当插入1和2之后,根节点为1,黑色;2为右孩子,红色;再插入3的时候,从1看来,出现了冲突,是RR型冲突,进行左旋,根节点就变成了2(红色),左孩子为1(黑色),右孩子为3(红色),因为代码中采用的调整策略是红色上浮,这个三元组会被修改为 红-黑-黑 结构,即 3 被修改为黑色,但是因为 2 是根节点,会强制将其修改为黑色,于是三个节点都变成了黑色。2是真正的根节点,并非局部根节点,它从红色变成黑色,会给每条路径上都增加一个黑色节点,但是因为它是根节点,所以每条路径上的黑色节点的数量还是相同的。
2.2 删除调整的情况
【分析】
删除红色节点,不会对红黑树的平衡产生影响;删除黑色节点会对红黑树平衡产生影响。
而删除黑色节点又分为三种情况:删除的度为0、1、2的节点。而删除度为2的节点可以转换为删除度为0或1的节点,所以只需要讨论两种情况即可:
- 删除的黑色节点是度为1的节点
例如下图所示,如果 xxx 为要删除的度为 1 的黑色节点,那么它的子节点一定为红色,因为以 xxx 为根节点的两棵子树的黑色节点数量要相同,现在 xxx 节点没有左子树,为了维持两棵子树的黑色节点数量相同都为0,所以 xxx 的右节点一定是红色。
即:删除的度为1的节点的子孩子一定是红色的
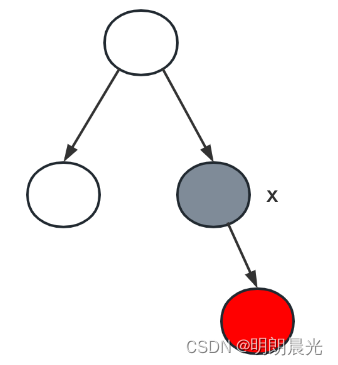
为了保证调整前后的黑色节点数量不变,所以删除黑色节点 xxx 后,将其子孩子挂到父节点上,并且将子孩子变成黑色。即是将删除的结点 xxx 的颜色加到唯一子孩子上。
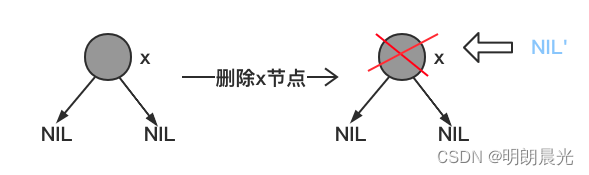
- 删除的黑色节点是度为0的节点
这种情况下就要使用到了 NIL 节点。如下左图所示,算上NIL节点,每条路径上 2 个黑色节点。但是当删除黑色节点后,取而代之的是一个新的 NIL 节点 NIL'(NIL'节点是个特殊的节点,被标记为黑色,但是它不是真实存在的节点),所以删除后每条路径上也要保证两个黑色节点,而 NIL'节点本身就是黑色,此时要做一个操作,将它标记为双重黑,才能保证每条路径上是两个黑色节点。也就是说将原来节点的黑色加到 NIL' 节点上,使得 NIL' 节点变成双重黑。

另一个关于"双重黑" 的解释图例:
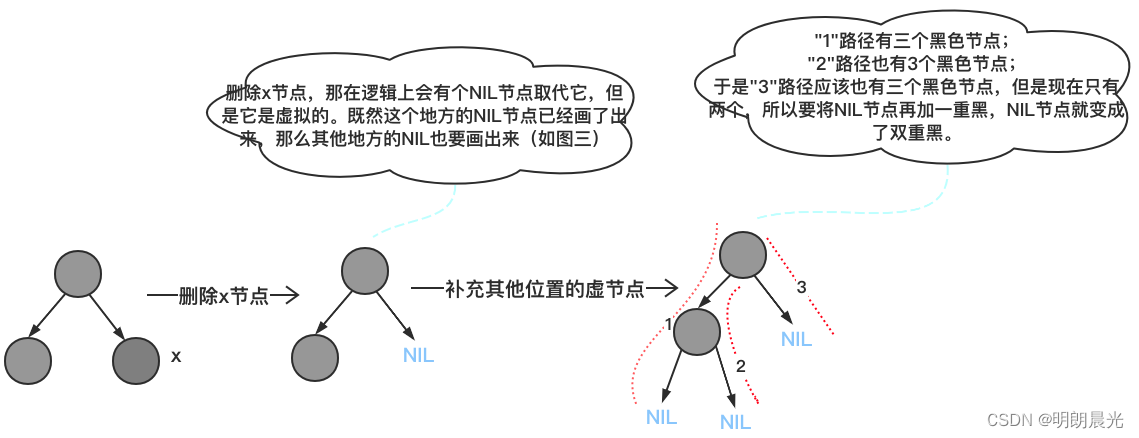
随着后续删除,这个双重黑的标记可能向上传递。
【结论】删除调整是为了干掉双重黑节点
2.2.1 情况一:双重黑节点的兄弟节点也是黑色,且其兄弟的两个孩子也是黑色
处理办法:
将双重黑的标记标记到父节点上(父节点加一重黑),父节点的两个子孩子各减一重黑,双重黑节点就变成正常黑,兄弟节点就变成红色。
下图中标记为 xxx 的节点就是双重黑节点,站在父节点(43)向下看,看到一个双重黑的节点,需要进行删除调整。
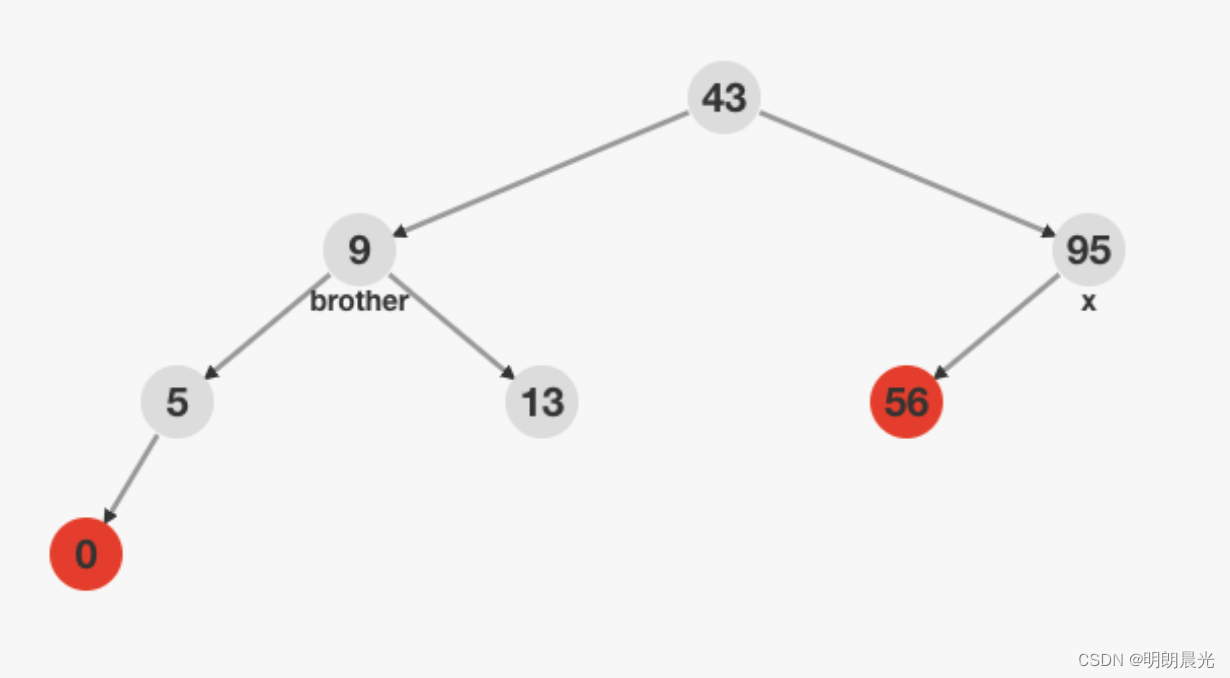
处理办法:brother 调整为红色,xxx 减少一重黑色,father 增加一重黑色。
2.2.2 情况二:双重黑节点的兄弟节点是黑色,兄弟节点存在红色的子节点
这种情况根据AVL失衡的情况进行划分:
1、兄弟节点在右侧,且兄弟节点的左侧是红色节点,兄弟节点的右子树一定是黑色,这种情况叫做RL
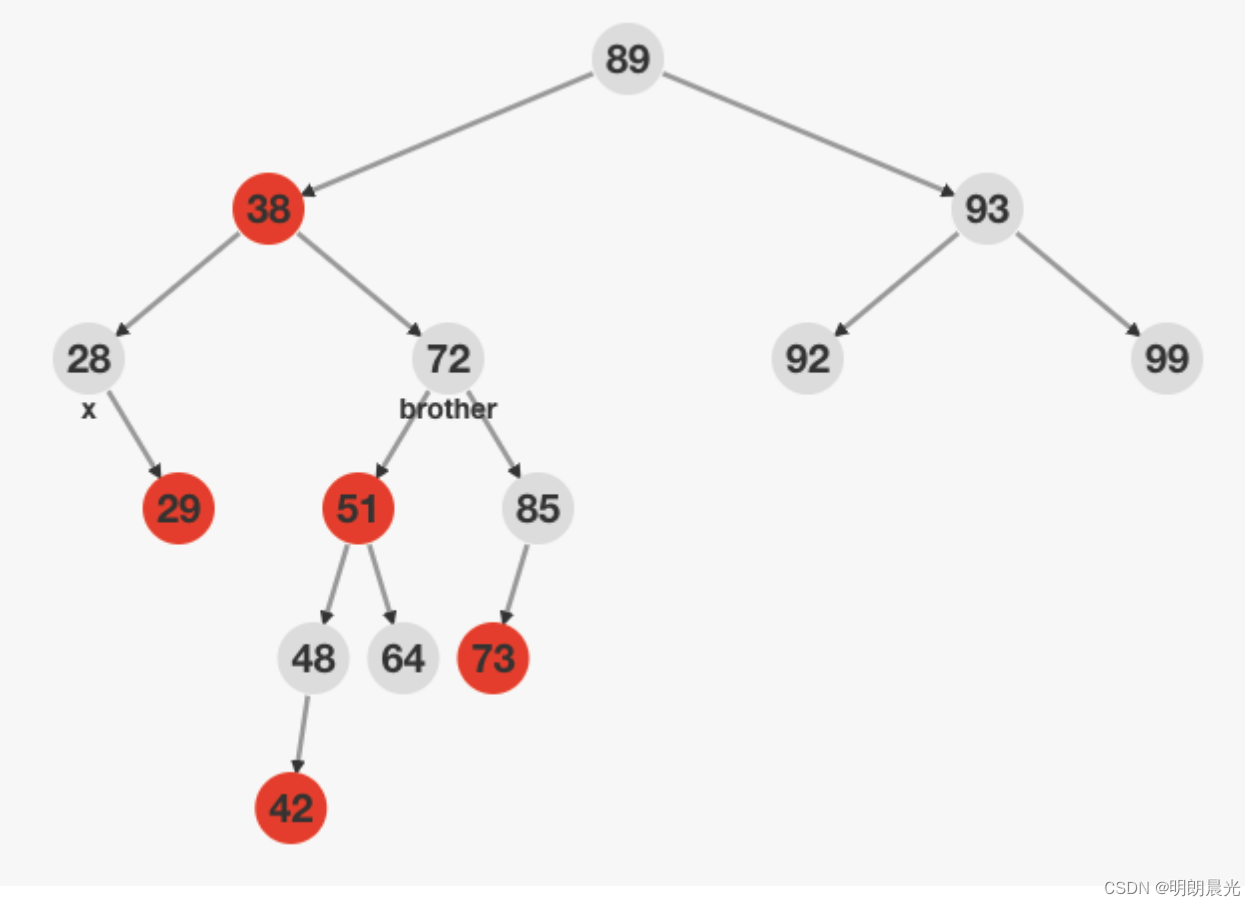
处理办法:右子树小右旋,转换为RR类型,抓着父节点进行大左旋。
子树 72 小右旋后的结果:
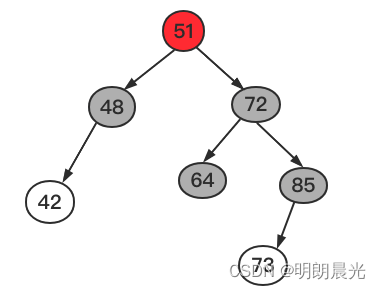
图中42和73的节点颜色是不确定的。旋转前,每棵子树上的黑色节点个数为2,旋转后经过颜色调整每棵子树上的黑色节点数量依然要为2。所以进行的颜色调整为:51变为黑色,72变为红色(因为64和85颜色是确定的黑色)。结合父节点38,就变成了RR类型。
2、兄弟节点在右侧,且兄弟节点的右侧是红色节点,无论兄弟节点的左侧节点是什么颜色,这种情况叫做RR,即情况三。
处理办法:抓住父节点左旋,然后修改颜色。
下图中,如果85是红色,就是RR类型,这种情况不管51的颜色。
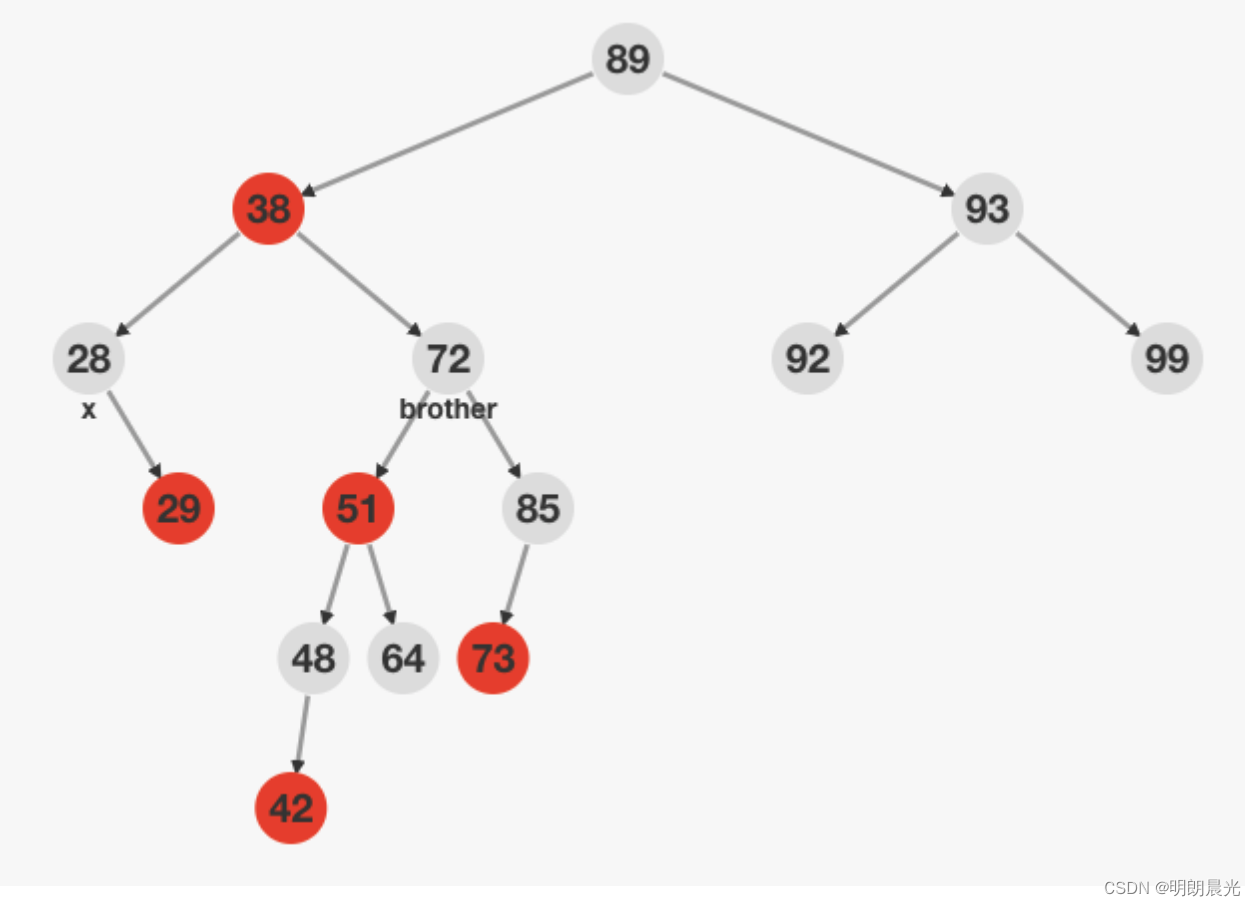
处理办法:brother 右(左)旋, 51 变黑, 72 变红,转成处理情况三
2.2.3 情况三
双重黑节点的兄弟节点在右子树且是黑色,且兄弟节点的右子树为红色(和兄弟节点在同一侧的,即兄弟节点在右子树上,兄弟节点的右子树上的节点是红色), 这种情况叫做RR。
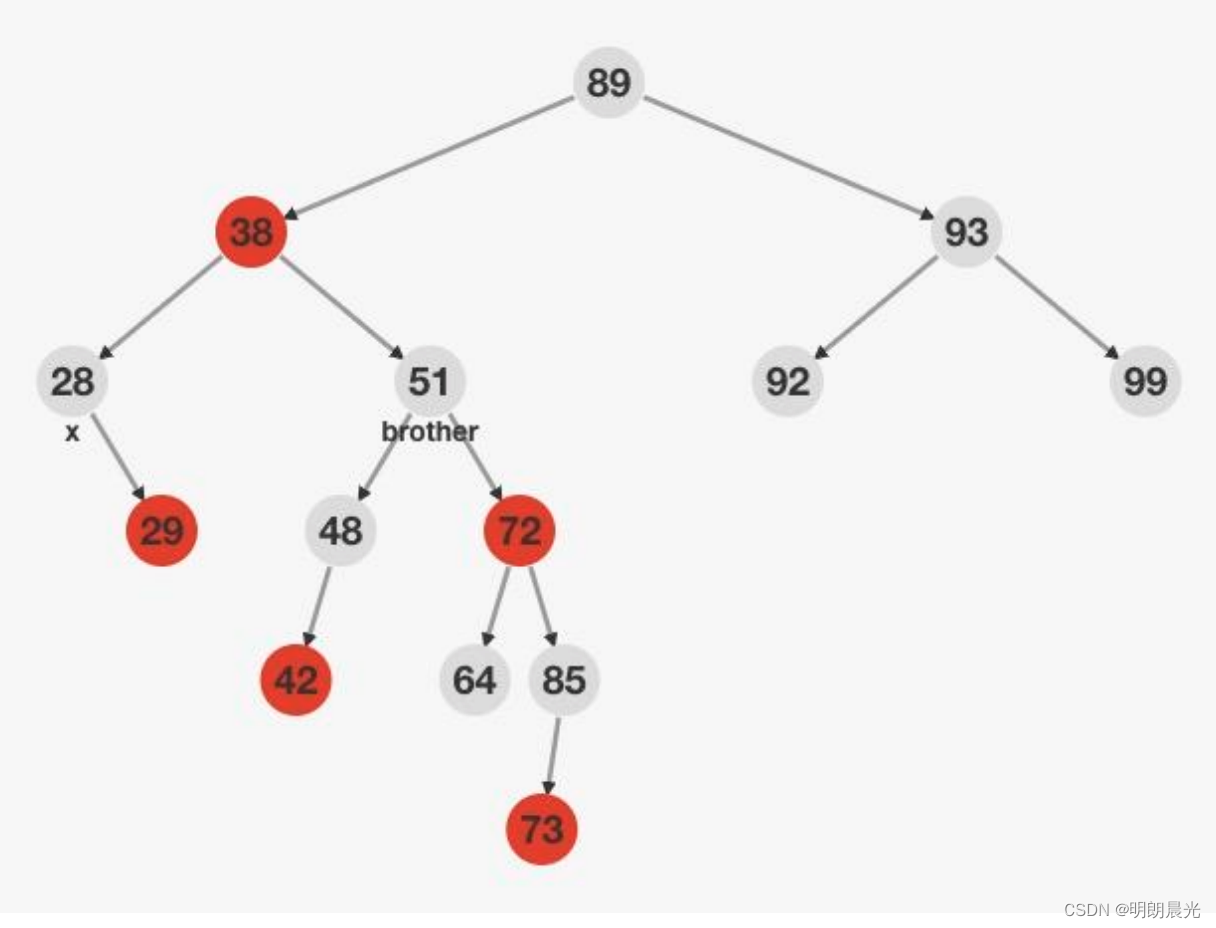
RR类型,抓着38节点进行左旋得到如下图所示:其中48节点的颜色是不确定。
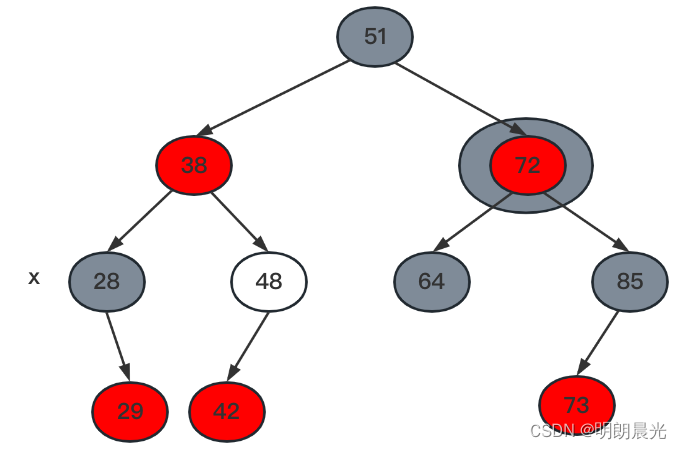
删除调整就是针对这棵经过左旋得到的树进行颜色修改,使得每棵子树旋转前后的黑色节点数量都为2。
修改颜色的思考过程:
因为48节点颜色不确定,如果48是红色,为了不发生冲突,只能将38改为黑色;又因为旋转前每条路径上是2个黑色节点,38一旦改成黑色,那么[51,38,28]这条路径上就变成了3个黑色节点,所以只能将51改成红色;而右侧每条路径上就变成了一个黑色节点,于是要将72改成黑色节点。
于是修改方法:51改成红色,38和72改成黑色。
但是这样修改有bug,如果38原来是黑色,那么51就得修改为红色,才能保证每条路径上两个黑色节点。
RR类型的修改方法:
双黑节点的父节点先大左旋,然后将左旋后的根节点颜色修改为原根节点的颜色,再把此时的子节点修改为黑色。
样例处理办法:father(38节点) 左(右)旋,由于无法确定 48 的颜色,所以38改成黑色, 51改成原38的颜色,x 减少一重黑色, 72改成黑色。
同理LL类型的调整策略类似。
2.2.4 思考:双黑节点的兄弟节点如果是红色,怎么办
如图,构建了一棵双黑节点的兄弟节点是红色的情况:
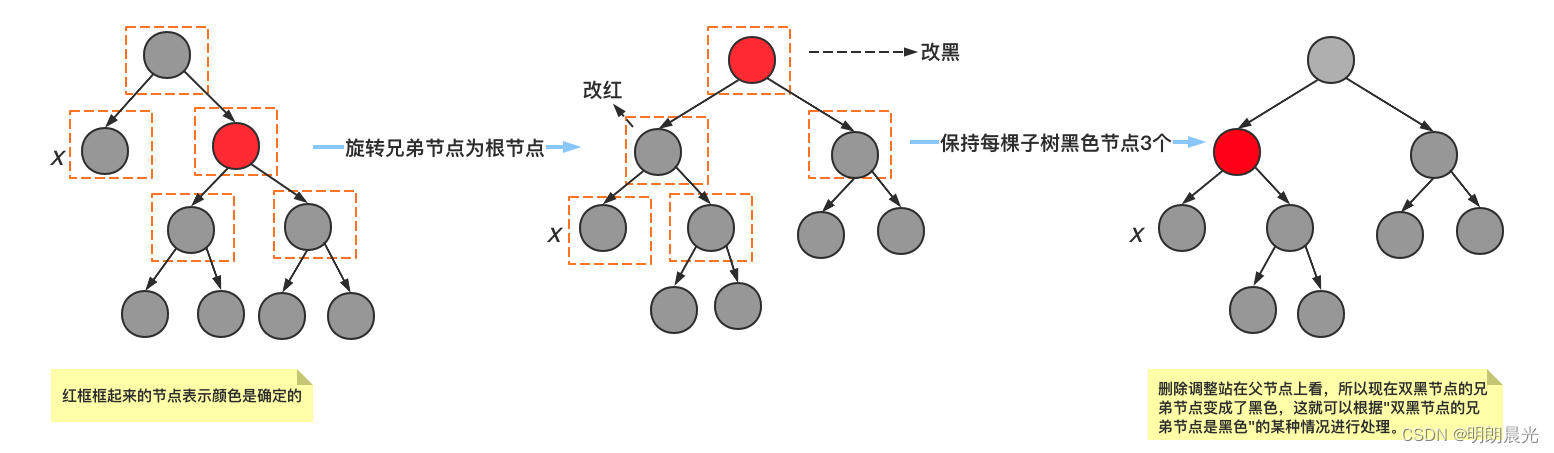
将其兄弟节点通过旋转成根节点,然后修改颜色,调整为双重黑节点的兄弟的节点为黑色的情况进行处理。
2.2.5 代码实现
//red_black_tree.cpp
#include <stdio.h>
#include <stdlib.h>
//包含红黑树的insert/erase操作
//完整版红黑树
typedef struct Node {int key;int color;//0 red, 1 black, 2 double blackstruct Node *lchild, *rchild;
} Node;Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void init_NIL() {NIL->key = 0;NIL->color = 1;NIL->lchild = NIL->rchild = NIL;return ;
}
//节点初始化
Node *getNewNode(int key) {Node *p = (Node *)malloc(sizeof(Node));p->key = key;p->color = 0;p->lchild = p->rchild = NIL;return p;
}int has_red_child(Node *root) {return root->lchild->color == 0 || root->rchild->color == 0;
}Node *left_rotate(Node *root) {Node *temp = root->rchild;root->rchild = temp->lchild;temp->lchild = root;return temp;
}Node *right_rotate(Node *root) {Node *temp = root->lchild;root->lchild = temp->rchild;temp->rchild = root;return temp;
}Node *insert_maintain(Node *root) {//当前节点没有红色子孩子,不会发生冲突,不需要做任何调整if (!has_red_child(root)) return root;//判断双红的情况:冲突发生在哪棵子树int flag = 0;//如果左右孩子都为红色,直接修改为红黑黑。处理插入情况1。//即便不发生冲突,这样修改也没有影响//这是一种偷懒的做法,因为没有判断是否发生了冲突if (root->lchild->color == 0 && root->rchild->color == 0) {//root->color = 0;//root->lchild->color = root->rchild->color = 1;//return root;goto insert_end;}//左孩子为红色,且左孩子的左孩子/右孩子也是红色(左子树发生了冲突)if (root->lchild->color == 0 && has_red_child(root->lchild)) flag = 1;//右孩子为红色,且右孩子的左孩子/右孩子也是红色(右子树发生了冲突)if (root->rchild->color == 0 && has_red_child(root->rchild)) flag = 2;//flag = 0表示没有发生冲突if (flag == 0) return root;if (flag == 1) {//L开头的失衡//判断是否为LR型,LR型需要先小左旋if (root->lchild->rchild->color == 0) {root->lchild = left_rotate(root->lchild);}root = right_rotate(root);} else { //R开头的失衡if (root->rchild->lchild->color == 0) {root->rchild = right_rotate(root->rchild);}root = left_rotate(root);}
insert_end://修改三元组小帽子的颜色(可以红色上浮或红色下沉的改法)//此处使用的是红色上浮的改法:红-黑-黑root->color = 0;root->lchild->color = root->rchild->color = 1;return root;
}//插入操作
Node *__insert(Node *root, int key) {if (root == NIL) return getNewNode(key);if (root->key == key) return root;if (key < root->key) {root->lchild = __insert(root->lchild, key);} else {root->rchild = __insert(root->rchild, key);}//回溯过程中进行插入调整return insert_maintain(root);
}//修改根节点的颜色为黑色
Node *insert(Node *root, int key) {root = __insert(root, key);root->color = 1;return root;
}Node *predecessor(Node *root) {Node *temp = root->lchild;while (temp->rchild != NIL) temp = temp->rchild;return temp;
}Node *erase_maintain(Node *root) {//删除节点站在父节点//左右节点都不是双重黑,不用调整if (root->lchild->color != 2 && root->rchild->color != 2) return root;//有双重黑节点且兄弟节点是红色if (has_red_child(root)) {int flag = 0;//原根节点给成红色root->color = 0;//将红色节点通过旋转成为根节点if (root->lchild->color == 0) {root = right_rotate(root);flag = 1;} else {root = left_rotate(root);flag = 2;}//新根节点改成黑色root->color = 1;//转换为兄弟节点是黑色的情况进行处理if (flag == 1) root->rchild = erase_maintain(root->rchild);else root->lchild = erase_maintain(root->lchild);return root;}//处理情况一://兄弟节点在右侧且兄弟节点没有红色子孩子//兄弟节点在左侧且兄弟节点没有红色子孩子if ((root->lchild->color == 2 && !has_red_child(root->rchild)) ||(root->rchild->color == 2 && !has_red_child(root->lchild))) {root->lchild->color -= 1;root->rchild->color -= 1;root->color += 1;return root;}if (root->lchild->color == 2) {root->lchild->color = 1;//右侧的兄弟节点的右节点颜色不为红色,若为红色就是RR,不需要进行小右旋//不能用root->rchild->rchild->color == 1,因为可能为NIL节点,可能是双重黑if (root->rchild->rchild->color != 0) {//RL//原根颜色变为红色root->rchild->color = 0;root->rchild = right_rotate(root->rchild);//新根颜色变为黑色root->rchild->color = 1;}root = left_rotate(root);root->color = root->lchild->color;} else {root->rchild->color = 1;if (root->lchild->lchild->color != 0) { //LRroot->lchild->color = 0;root->lchild = left_rotate(root->lchild);root->lchild->color = 1;}root = right_rotate(root);root->color = root->rchild->color;}root->lchild->color = root->rchild->color = 1;return root;
}Node *__erase(Node *root, int key) {if (root == NIL) return NIL;if (key < root->key) {root->lchild = __erase(root->lchild, key);} else if (key > root->key) {root->rchild = __erase(root->rchild, key);} else {//删除度为0或1的节点if (root->lchild == NIL || root->rchild == NIL) {Node *temp = root->lchild != NIL ? root->lchild : root->rchild;//将当前节点颜色加到唯一子孩子上//如果root为红色,对子孩子颜色没有影响;//如果root为黑色,就要将这个颜色加到唯一子孩子上temp->color += root->color;free(root);return temp;} else { //删除度为2的节点Node *temp = predecessor(root);root->key = temp->key;root->lchild = __erase(root->lchild, temp->key);}}return erase_maintain(root);
}Node *erase(Node *root, int key) {root = __erase(root, key);root->color = 1;return root;
}//销毁操作
void clear(Node *root) {if (root == NIL) return ;clear(root->lchild);clear(root->rchild);free(root);return ;
}void print(Node *root) {printf("(%d| %d, %d %d)\n", root->color, root->key, root->lchild->key, root->rchild->key);return ;
}void output(Node *root) {if (root == NIL) return ;print(root);output(root->lchild);output(root->rchild);return ;
}int main() {int op, val;Node *root = NIL;while (~scanf("%d%d", &op, &val)) {switch (op) {case 1: root = insert(root, val); break;case 2: root = erase(root, val); break;}output(root);printf("------------\n");}return 0;
}
运行测试1:
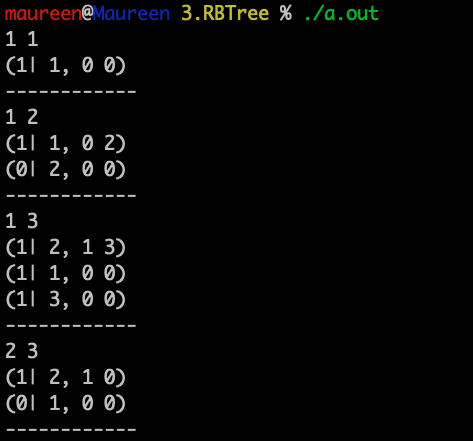
结果分析:这就是兄弟节点为黑色,且兄弟节点的两个子节点都为黑色,处理方案就是将父节点加一重黑,子节点各减一重黑,所以兄弟那个节点就变为红色,此处即是1变为红色。而父节点此时是根节点,所以会被强制变为正常黑。
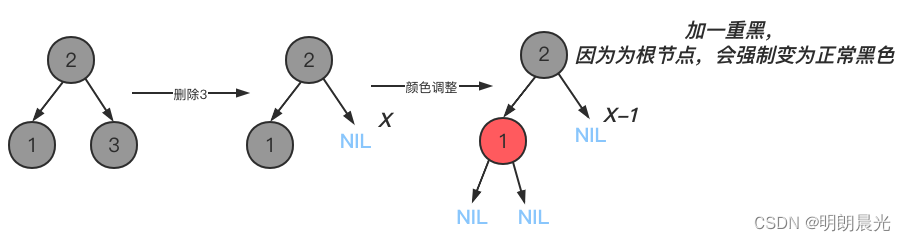
运行测试2:
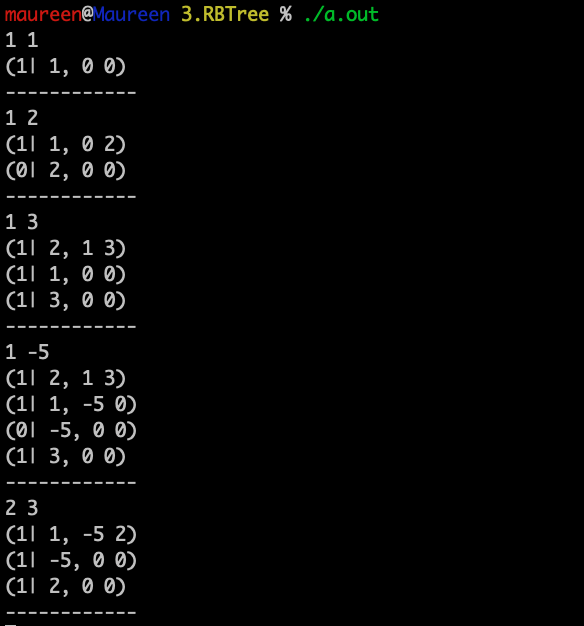
结果分析:删除3节点后,用NIL节点替代3,且被标记为双重黑;其兄弟节点在左侧为黑色,且兄弟节点的左孩子为红色,就是LL类型,所以进行大右旋。右旋之后,将新根节点修改为原根节点的颜色;新根节点的孩子节点修改为黑色。
3、总结
3.1 平衡条件
- 节点非黑即红
- 根节点是黑色
- 叶子(NIL) 结点是黑色
- 红色节点下面接两个黑色节点
- 从根节点到叶子节点路径上,黑色节点数量相同
平衡条件的认识
第4和5条注定了红黑树中最长路径是最短路径的2倍。
本质上,红黑树也是通过树高来控制平衡的。
红黑树比AVL树树高控制条件要更松散,红黑树在发生节点插入和删除以后,发生调整的概率,比AVL树要更小。
3.2 学习诀窍
- 理解红黑树的插入调整,要站在 祖父节点 向下进行调整
- 理解红黑树的删除调整,要站在 父节点 向下进行调整
- 插入调整,主要就是为了解决双红情况
- 新插入的节点一定是红色。插入黑色节点一定会产生冲突,违反条件5;插入红色节点,不一定产生冲突
- 把每一种情况,想象成一棵大的红黑树中的局部子树
- 局部调整的时候,为了不影响全局,调整前后每条路径上黑色节点的数量相同
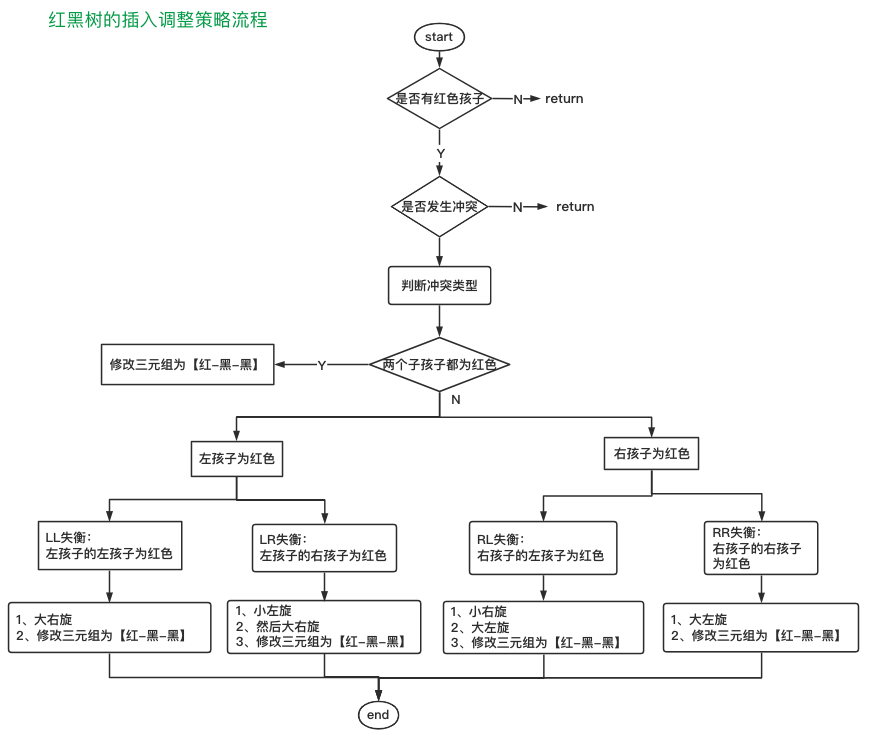
3.3 插入策略
- 叔叔节点为红色的时候,修改三元组小帽子,改成红黑黑
- 叔叔节点为黑色的时候,参考AVL树的失衡情况,分成 LL,LR,RL,RR,先参考AVL树的旋转调整策略,然后再修改三元组的颜色,有两种调整策略:红色上浮,红色下沉。
- 两大类情况,包含8种小情况
3.4 插入调整代码重点
- 插入调整,发生在递归的回溯阶段
- 插入调整代码中,使用
goto语句,8行代码变成了4行 - 处理根节点一定是黑色,通过代码封装,
insert->__insert
3.5 删除调整发生的前提
- 删除红色节点不会对红黑树的平衡产生影响
- 度为1的黑色节点,唯一子孩子一定是红色
- 删除度为1的黑色节点,不会产生删除调整
- 删除度为0的黑色节点,会产生一个双重黑的NIL节点
- 删除调整,就是为了干掉双重黑
3.6 删除调整
- 双重黑节点的兄弟节点是黑色,兄弟节点下面的两个子节点也是黑色,父节点增加一重黑色,双重黑与兄弟节点分别减少一重黑色。
- 双重黑节点的兄弟节点是黑色,并且,兄弟节点中有红色子节点
- R(兄弟)R(右子节点),左旋,新根改成原根的颜色,将新根的两个子节点改成黑色,双重黑节点改成一重黑;
- R(兄弟)L(左子节点),先小右旋,对调新根与原根的颜色,转成上一种情况;
- LL 同理 RR
- LR 同理 RL
- 双重黑节点的兄弟节点是红色,通过旋转,转变成兄弟节点是黑色的情况

3.7 删除调整代码重点
进行LR/RL类型判断的时候,不能判断 LL 子树是否为黑色,因为LL子树有可能是NIL节点,在某些特殊情况下,读到的颜色可能是双重黑,取而代之的判断方法是【LL子树不是红色】
相关文章:

有序表之红黑树
文章目录1、五个条件2、调整策略2.1 插入调整的情况2.1.1 情况一:插入节点是红色,其父节点也是红色2.1.2 情况二2.1.2 代码实现2.2 删除调整的情况2.2.1 情况一:双重黑节点的兄弟节点也是黑色,且其兄弟的两个孩子也是黑色2.2.2 情…...

HTTP状态码都有哪些?
100:客户必须继续发出请求 101:客户要求服务器根据请求转换HTTP协议版本 二:2xx 200:交易成功 201:提示知道新文件的URL 202:接受和处理、但处理未完成 203:返回信息不确定或不完整 204&#…...

Sketch+摹客,100M文件上传最快47s
哈喽,小摹来啦~ 去年12月底,摹客Sketch插件上新了「规范检查工具」,自功能上线以来,小摹收到了许多的好评及赞扬。 虽好评如潮,但我们不会止步不前,将持续攻克难点,旨在为大家提供更加稳定高效…...

关系型数据之分区分表分库
文章目录1.为什么需要分区分表分库2.各种分区分表分库的情况3.弊端3.1分区弊端3.2分表分库弊端1.为什么需要分区分表分库 数据量达到一定规模,进行常规的sql语句优化已经效果不大的情况下,常见为mysql数据库,单表的记录达到1000W和空间占用至…...

微信小程序:基本开发相关文档
1、微信公众平台(后台登录页):https://mp.weixin.qq.com/2、微信小程序官网文档(组件api等):https://developers.weixin.qq.com/miniprogram/dev/component/audio.html3、微信开放社区(问题社区…...

Win10关闭自动更新
Win10关闭自动更新第一步:修改电脑系统时间第二步,设置自动更新时间第三步:再次修改系统时间为正确时间因为国内使用的操作系统,很多是非正版的系统,如果更新了系统,很容易造成电脑蓝屏,系统运…...

Embedding 理解
Word Embedding 单词表示最简单的是 one-hot 但是它的缺点是 矩阵表示过于稀疏,占用空间对相关的词语无法得知它们的含义是相近的。 Word Embedding 解决了上述两个缺点,一个 Word Embedding 直观的例子如下图所示。 每个维度表示一个特征࿰…...

工业树莓派和PLC怎么选?
一、 什么是虹科工业树莓派 1、树莓派 在了解虹科工业树莓派之前,首先要了解一下什么是树莓派。树莓派是一款基于ARM的小型电脑,在树莓派上提供丰富的接口,能够实现较多功能。它同样是开发人员的最爱,其搭载Linux系统࿰…...
多层感知机的区间随机初始化方法
摘要: 训练是构建神经网络模型的一个关键环节,该过程对网络中的参数不断进行微调,优化模型在训练数据集上的损失函数。参数初始化是训练之前的一个重要步骤,决定了训练过程的起点,对模型训练的收敛速度和收敛结果有重要…...

分析JEP 290机制的Java实现
简介 https://openjdk.org/jeps/290 Filter Incoming Serialization Data过滤传入的序列化数据 JEP290是Java官方提供的一套来防御反序列化的机制,其核心在于提供了一个ObjectInputFilter接口,通过设置filter对象,然后在反序列化ÿ…...

Leetcode.2140 解决智力问题
题目链接 Leetcode.2140 解决智力问题 Rating : 1709 题目描述 给你一个下标从 0开始的二维整数数组 questions,其中 questions[i] [pointsi, brainpoweri]。 这个数组表示一场考试里的一系列题目,你需要 按顺序 (也就是从问题…...

新时代下的医疗行业新基建研讨会
1、会议纪要 2023年2月17日,HIT专家网进行了《新时代下的医疗行业新基建研讨会》的会议。 对会议内容进行了记录。 会议中有友谊医院、301、北肿主任进行了分享。大纲如下所示 2、本人所想 本人的所想所感: 1、301在多院区的医疗信息建设,…...
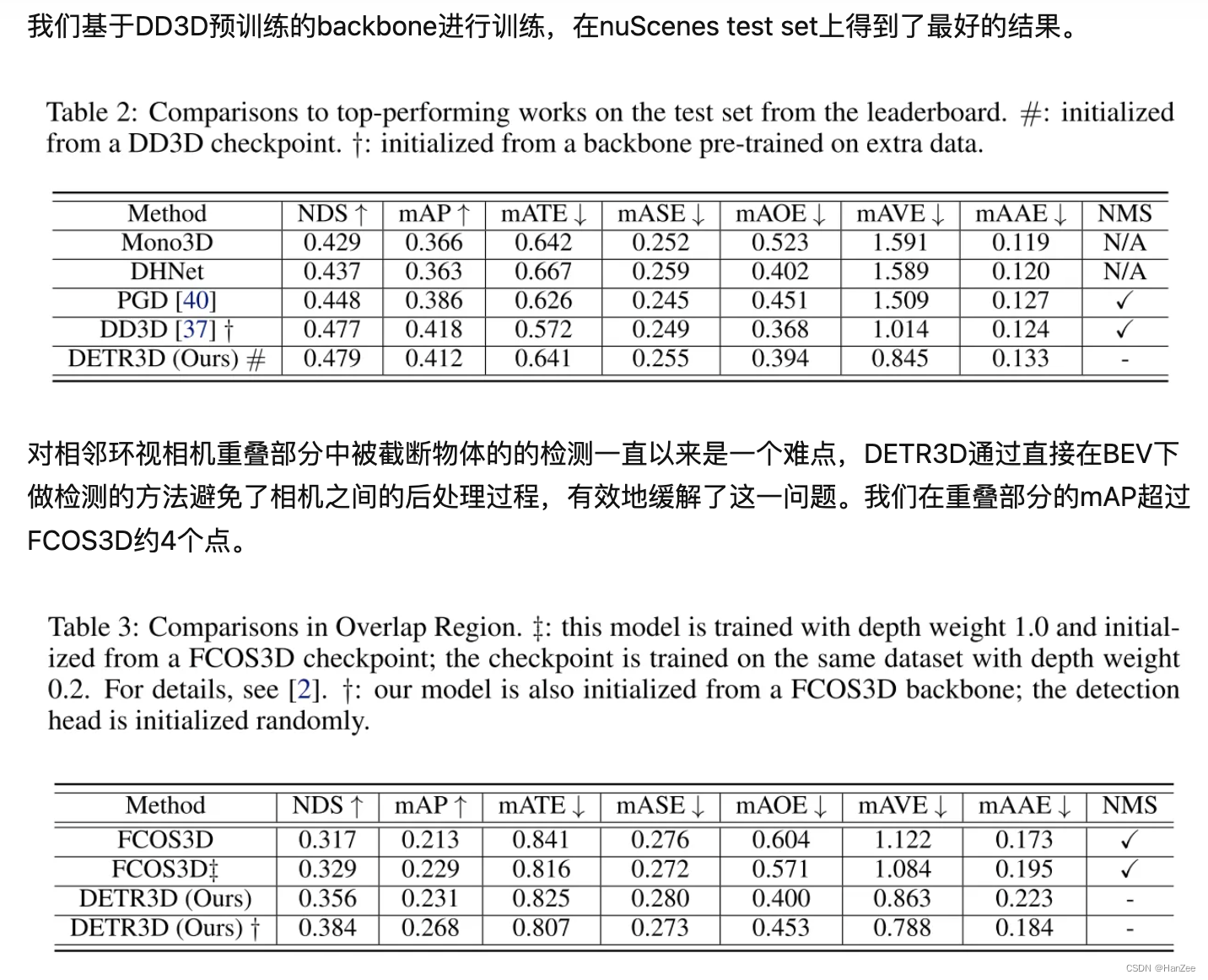
BEV感知:DETR3D
3D检测:DETR3D前言MethodImage Feature Extracting2D-to-3D Feature TransformationLoss实验结果前言 在这篇paper,作者提出了一个更优雅的2D与3D之间转换的算法在自动驾驶领域,它不依赖于深度信息的预测,这个框架被称之为DETR3D…...

亿级高并发电商项目-- 实战篇 --万达商城项目 十二(编写用户服务、发送短信功能、发送注册验证码功能、手机号验证码登录功能、单点登录等模块)
👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信支付、若依框架、Spring全家桶 Ǵ…...

整合spring cloud云服务架构 - 企业分布式微服务云架构构建
1. 介绍 Commonservice-system是一个大型分布式、微服务、面向企业的JavaEE体系快速研发平台,基于模块化、服务化、原子化、热插拔的设计思想,使用成熟领先的无商业限制的主流开源技术构建。采用服务化的组件开发模式,可实现复杂的业务功能。…...

leetcode 540. Single Element in a Sorted Array(排序数组中的单个元素)
给一个已经排好序的升序数组,其中每个元素都会重复2次,只有一个元素只有一个, 找出这个只有一个的元素。 要求时间复杂度在O(logn), 空间复杂度在O(1). 思路: 时间复杂度为O(logn), 让人想到了binary search. 因为时间复杂度为…...

Color correction for tone mapping
Abstract色调映射算法提供了复杂的方法,将真实世界的亮度范围映射到输出介质的亮度范围,但它们经常导致颜色外观的变化。在本研究中,我们进行了一系列的主观外观匹配实验,以测量对比度压缩和增强后图像色彩的变化。结果表明&#…...
JavaScript-XHR-深入理解
JavaScript-XHR-深入理解1. XHR(Asynchronous JavaScript And XML)初始1.1. xhr request demo1.2. status of XHRHttpRequest1.3. send synchronous request by xhr1.4. onload监听数据加载完成1.5. http status code1.6. get/post request with josn/form/urlcoded1.7. encaps…...
mathtype7.0最新版安装下载及使用教程
MathType是一款专业的数学公式编辑器,理科生专用的必备工具,可应用于教育教学、科研机构、工程学、论文写作、期刊排版、编辑理科试卷等领域。2014年11月,Design Science将MathType升级到MathType 6.9版本。在苏州苏杰思网络有限公司与Design…...

响应状态码
✨作者:猫十二懿 ❤️🔥账号:CSDN 、掘金 、个人博客 、Github 🎉公众号:猫十二懿 一、状态码大类 状态码分类说明1xx响应中——临时状态码,表示请求已经接受,告诉客户端应该继续请求或者如果…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
