POJ 3662 Telephone Lines 二分,最小化第k大的数
一、题目大意
我们有n个点,p条边,最小化从1到n之间的路径的第k+1大的数(当路径不超过k时就是0)
二、解题思路
我们首先用dijkstra过一遍,判断从1能不能到n,不能直接输出-1结束。
1能到达n的话,就对二分第k+1大的边进行二分,left选-1,right选最大的边的长度+1(这里我left一开始选取的时最小边-1,后来发现当k比较大时结果可能是0)
二分的依据如下
设二分的值为mid
记录从1到n的路径中必走的大于mid的值的数量
如果超过了k,那么放大mid
如果小于等于k,那么缩小mid,同时记录这样不断循环,直到找到一个临界值limit
当mid=limit时,大于mid的边小于等于k个
当mid=limit-1时,大于mid的边超过k个
那么limit一定就是第k+1大的边输出最后一个(大于mid的边数小于等于k的)mid即可三、代码
#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
typedef pair<int, int> P;
vector<P> edges[1007];
bool used[1007];
int n, p, k, d[1007], inf = 0x3f3f3f3f, maxt = 0;
void input()
{int from, to, cost;scanf("%d%d%d", &n, &p, &k);for (int i = 0; i < p; i++){scanf("%d%d%d", &from, &to, &cost);edges[from - 1].push_back(P(cost, to - 1));edges[to - 1].push_back(P(cost, from - 1));maxt = max(cost, maxt);}
}
bool judgeByDijkstra(int mid)
{for (int i = 0; i < n; i++){d[i] = inf;used[i] = false;}d[0] = 0;priority_queue<P, vector<P>, greater<P>> que;que.push(P(d[0], 0));while (!que.empty()){P current = que.top();que.pop();if (used[current.second] || current.first > d[current.second]){continue;}used[current.second] = true;for (int i = 0; i < edges[current.second].size(); i++){P toEdge = edges[current.second][i];int relativeEdge = toEdge.first > mid ? 1 : 0;if (d[current.second] + relativeEdge < d[toEdge.second]){d[toEdge.second] = d[current.second] + relativeEdge;que.push(P(d[toEdge.second], toEdge.second));}}}return d[n - 1] <= k;
}
void binarySearch()
{int left = -1, right = maxt + 1;while (left + 1 < right){int mid = (left + right) / 2;if (judgeByDijkstra(mid)){right = mid;}else{left = mid;}}printf("%d\n", right);
}
bool judgeIfCanGet()
{for (int i = 0; i < n; i++){d[i] = inf;used[i] = false;}d[0] = 0;priority_queue<P, vector<P>, greater<P>> que;que.push(P(d[0], 0));while (!que.empty()){P current = que.top();que.pop();if (used[current.second] || current.first > d[current.second]){continue;}used[current.second] = true;for (int i = 0; i < edges[current.second].size(); i++){P toEdge = edges[current.second][i];if (d[current.second] + toEdge.first < d[toEdge.second]){d[toEdge.second] = d[current.second] + toEdge.first;que.push(P(d[toEdge.second], toEdge.second));}}}return d[n - 1] != inf;
}
int main()
{input();if (!judgeIfCanGet()){printf("-1\n");}else{binarySearch();}return 0;
}相关文章:

POJ 3662 Telephone Lines 二分,最小化第k大的数
一、题目大意 我们有n个点,p条边,最小化从1到n之间的路径的第k1大的数(当路径不超过k时就是0) 二、解题思路 我们首先用dijkstra过一遍,判断从1能不能到n,不能直接输出-1结束。 1能到达n的话࿰…...
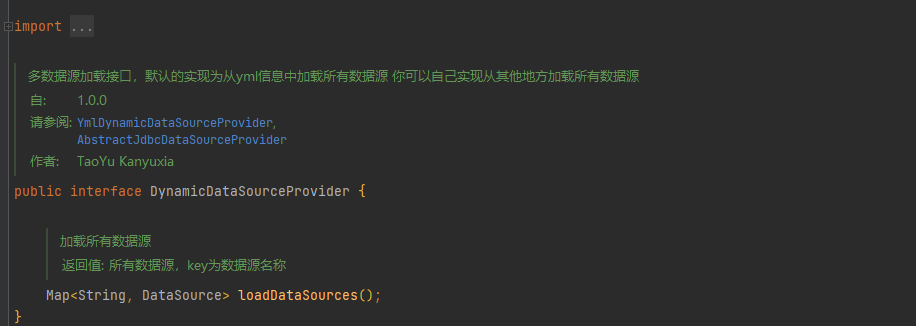
【mybatis-plus进阶】多租户场景中多数据源自定义来源dynamic-datasource实现
Springbootmybatis-plusdynamic-datasourceDruid 多租户场景中多数据源自定义来源dynamic-datasource实现 文章目录 Springbootmybatis-plusdynamic-datasourceDruid 多租户场景中多数据源自定义来源dynamic-datasource实现0.前言1. 作者提供了接口2. 基于此接口的抽象类实现自…...

vue3 async await
const getStruct async () > {//首先从store读取,否则通过接口获取if (store.state.struct.v ! null) {return store.state.struct.v;} else {const data await getStructApi();store.dispatch("struct/keepV", data).then(() > {console.log(&qu…...
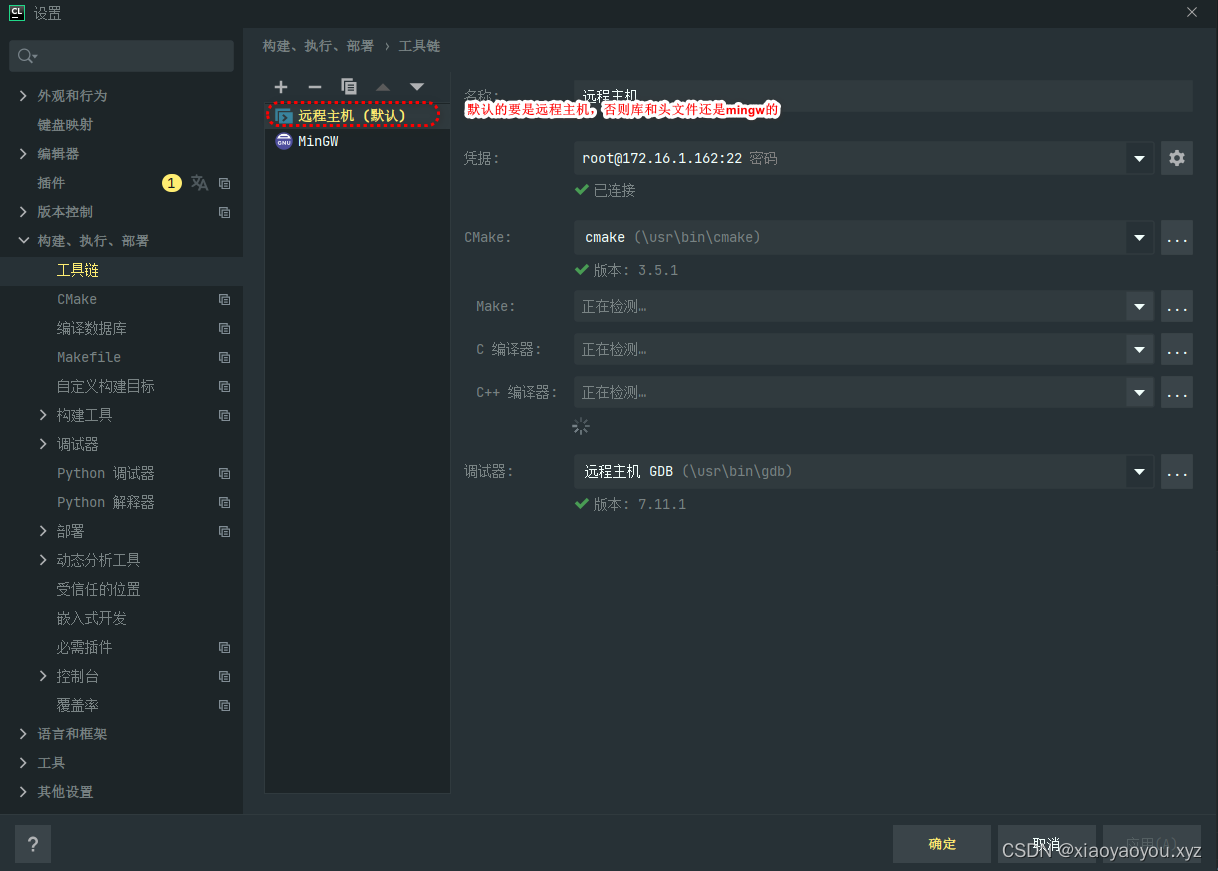
CLion远程Linux开发环境搭建及找不到Linux头文件的解决方法
CLion远程开发环境搭建及找不到Linux头文件的解决方法 文章目录 CLion远程开发环境搭建及找不到Linux头文件的解决方法1.前言2.远程开发3.远程编译4.远程调试5.远程开发Linux头文件找不到(比如pthread.h、<sys/socket.h>)6.最后 1.前言 在某些时候…...
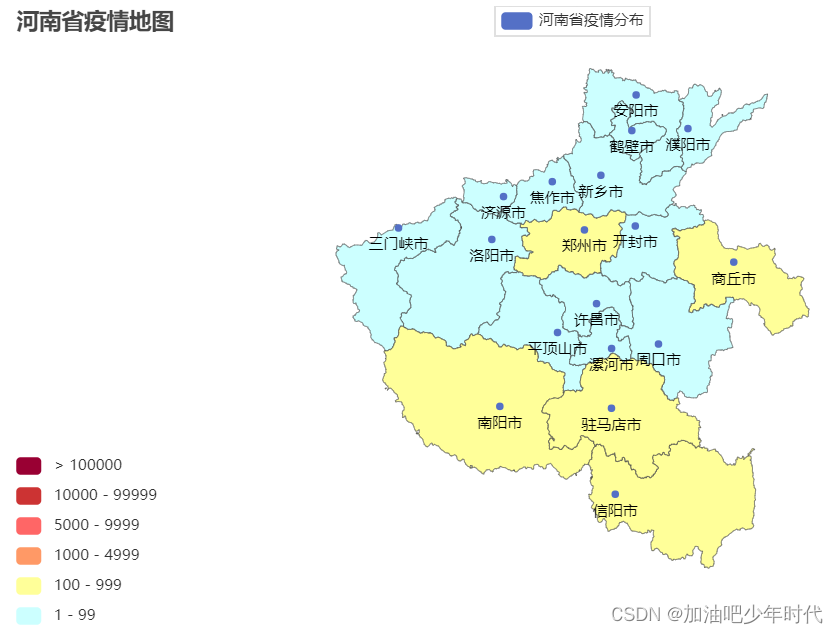
Python综合案例(基本地图使用)
一、基本地图的使用 基本代码: """ 演示地图可视化的基本使用 """ from pyecharts.charts import Map from pyecharts.options import VisualMapOpts# 准备地图对象 map Map() # 准备数据 data [("北京", 99),("…...

maven的scope总结
scope类型 compiletestprovidedruntimesystemimport compile 编译依赖范围。如果没有指定,就会默认使用该依赖范围。使用此依赖范围的Maven 依赖,对于编译、测试、运行三种classpath 都有效。大部分是这种,在编译、测试和运行的时候都需要使…...

Linux执行命令
命令格式 主命令 选项 参数(操作对象)例如: 修改主机名 hostname set-hostname 新名称显示/目录下的文件的详细信息 ls -l /命令 内置命令(builtin):shell程序自带的命令。 外部命令:有独立…...

Nginx 配置中root和alias的区别分析
root和alias都可以定义在location模块中,都是用来指定请求资源的真实路径,比如: location /i/ { root /data/w3; } 请求 http://foofish.net/i/top.gif 这个地址时,那么在服务器里面对应的真正的资源 是 /data/w3/i/top.gif文…...
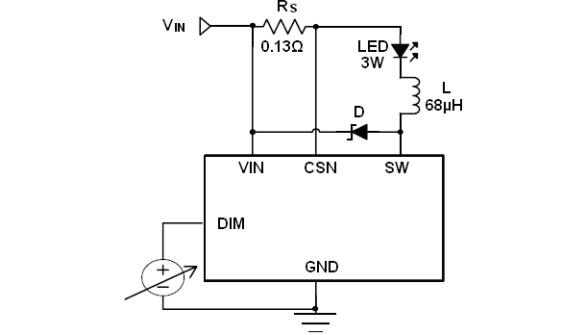
AP51656 PWM和线性调光 LED车灯电源驱动IC 兼容替代PT4115 PT4205
产品描述 AP51656是一款连续电感电流导通模式的降压恒流源 用于驱动一颗或多颗串联LED 输入电压范围从 5V 到 60V,输出电流 可达 1.5A 。根据不同的输入电压和 外部器件, 可以驱动高达数十瓦的 LED。 内置功率开关,采用高端电流采样设置 …...
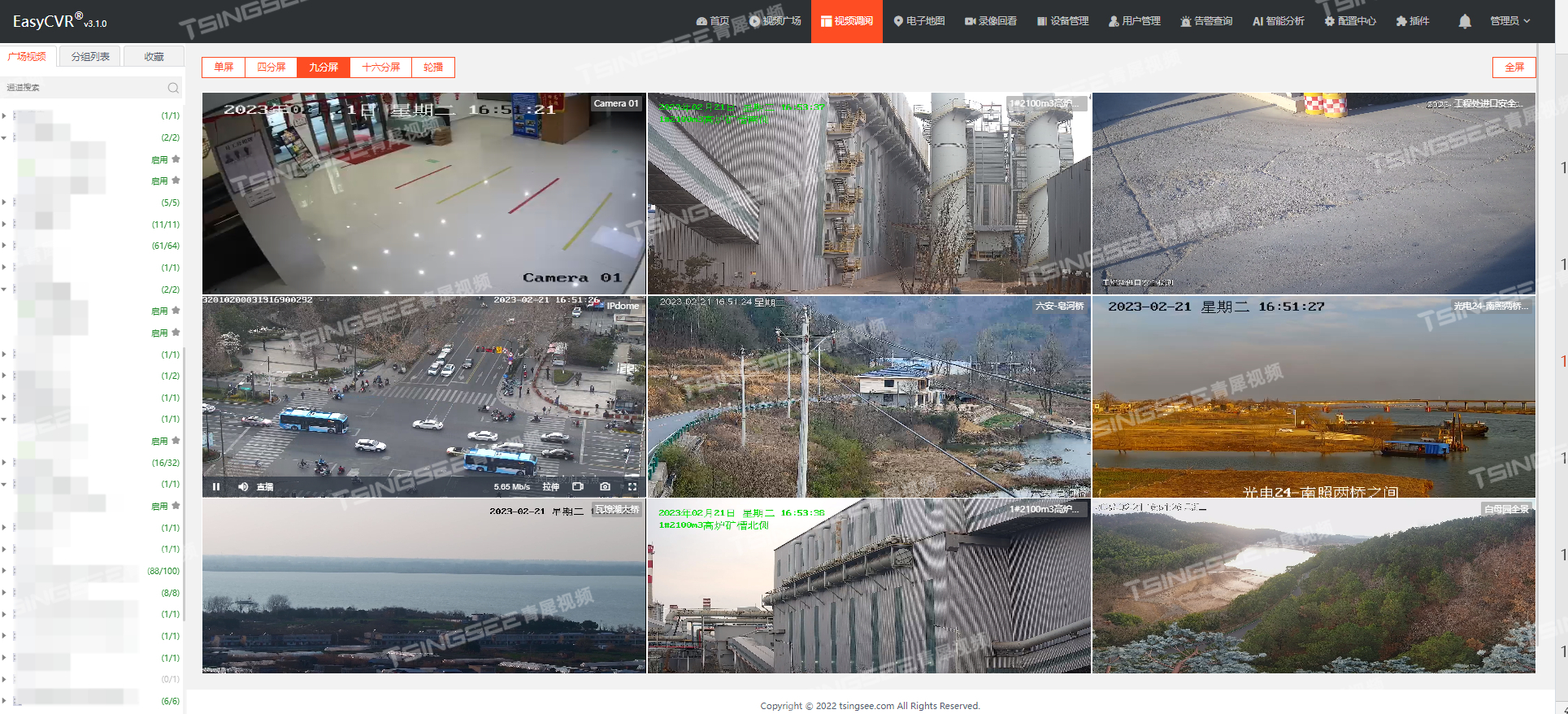
视频汇聚/视频云存储/视频监控管理平台EasyCVR部署后无法正常启用是什么问题?该如何解决?
安防监控/视频监控/视频汇聚平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,在视频监控播放上,视频云存储/安防监控汇聚平台EasyCVR支持多种播放协议,包括:HLS、HTTP-FLV、WebSoc…...

Kubernetes v1.25.0集群搭建实战案例(新版本含Docker容器运行时)
k8s 1.24之后弃用了docker容器运行时,安装方式上有所不同,网上找到的大多数都是1.24之前的版本。所以把自己搭建的完整过程记录下来供大家参考。 一、前言 k8s的部署方式有多种kubeadm、kind、minikube、Kubespray、kops等本文介绍官方推荐的kubeadm的…...

RabbitMQ、Kafka和RocketMQ比较
一、概述 消息队列中间件(MQ)是不同系统之间消息传递,异步通信的常见组件,RabbitMQ、Kafka和RocketMQ是目前业界常见的3种消息中间件,本文重点阐述了他们特性差异、架构设计和处理常见问题的方案。 二、特性比较 Ra…...

http和https区别,第三方证书如何保证服务器可信
HTTP(Hypertext Transfer Protocol)和HTTPS(HTTP Secure)是用于在客户端和服务器之间传输数据的协议,它们在以下几个方面有所区别: 安全性:HTTP是明文协议,数据在传输过程中不加密&…...
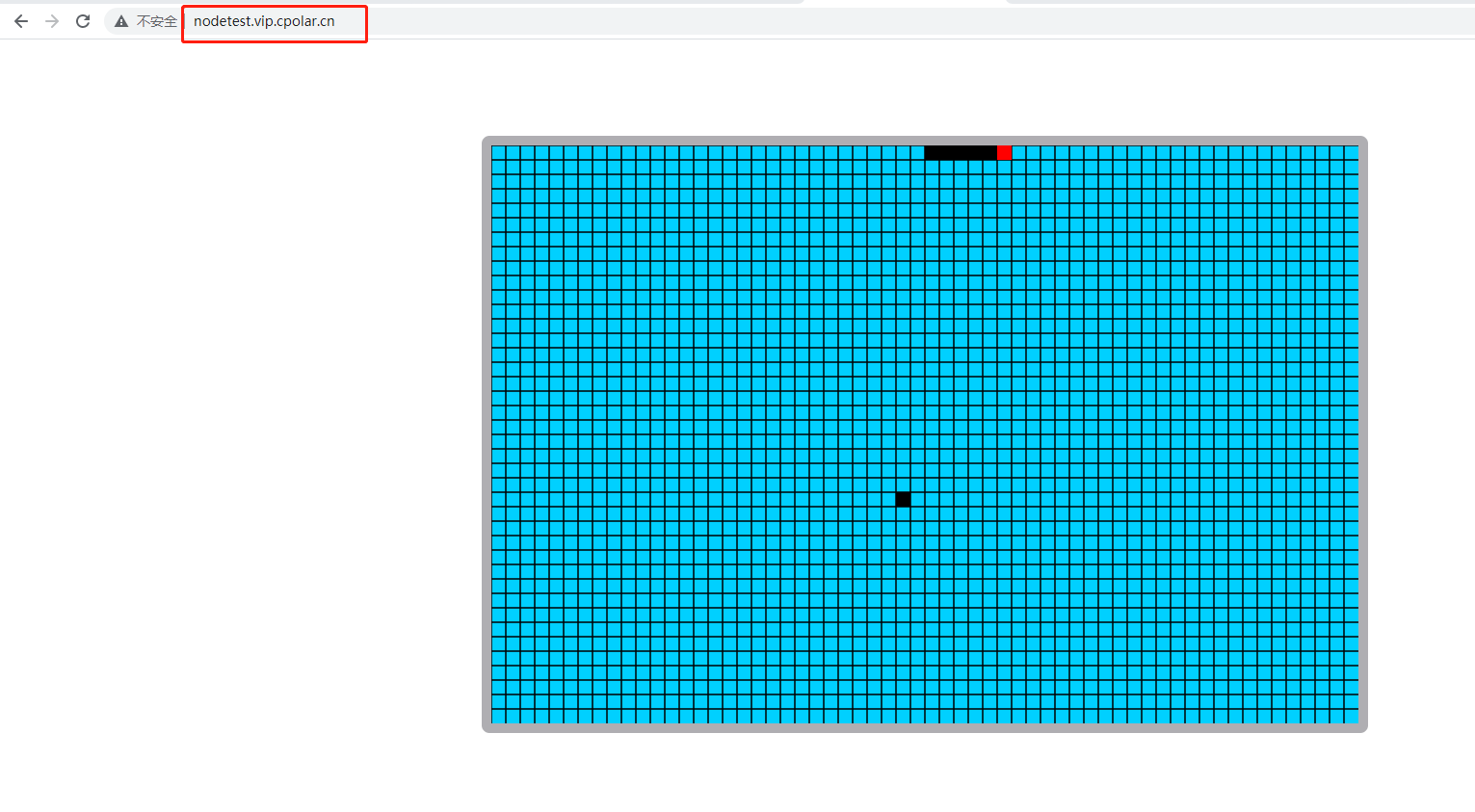
【内网穿透】使用Nodejs搭建简单的HTTP服务器 ,并实现公网远程访问
目录 前言 1.安装Node.js环境 2.创建node.js服务 3. 访问node.js 服务 4.内网穿透 4.1 安装配置cpolar内网穿透 4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation…...

Linux中的多线程剖析
目录 1、前言 2、多线程理解 2.1 线程 2.2 通俗了解进程和线程 2.2.1 进程是资源分配的基本单位 2.2.2 Linux中的线程是一种轻量化进程 2.3 进程和线程详解 2.3.1 创建一个线程 (pthread_create) 2.3.2 线程自己的一部分数据 2.3.3 线程组 2.3.4 关于进程的其他操作…...

uniapp 集成蓝牙打印功能(个人测试佳博打印机)
uniapp 集成蓝牙打印功能(个人测试京博打印机) uniapp 集成蓝牙打印功能集成佳博内置的接口 uniapp 集成蓝牙打印功能 大家好今天分析的是uniapp 集成蓝牙打印功能,个人开发是app,应该是支持H5(没试过) 集成佳博内置的接口 下载dome地址&…...
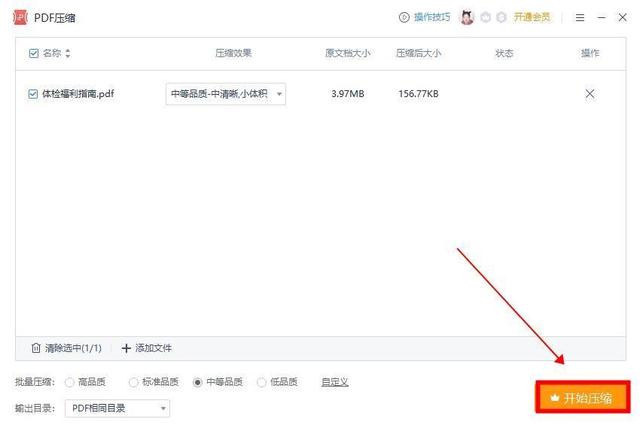
pdf文件过大如何缩小上传?pdf压缩跟我学
在我们日常工作和生活中,经常会遇到PDF文件过大的问题,给文件传输和存储带来了很大的不便。那么,如何缩小PDF文件大小以便上传呢?下面就给大家分享几个压缩方法,一起来了解下PDF文件压缩方法吧~ 方法一:嗨格…...
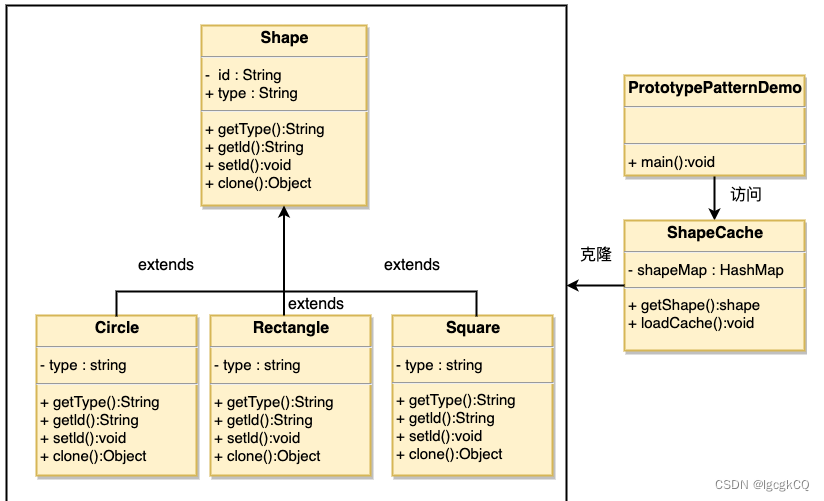
设计模式之建造者模式与原型模式
目录 建造者模式 简介 使用场景 优缺点 模式结构 实现 原型模式 简介 应用场景 优缺点 模式结构 实现 建造者模式 简介 将复杂对象的构建与表示进行分离,使得同样的构建过程可以创建不同的表示。是一个将复杂的对象分解为多个简单的对象,然…...
合并到pdf怎么合并?这个方法了解一下
在现代数字化时代,PDF(便携式文档格式)已成为最常用的文件格式之一。PDF文件的优点在于其跨平台兼容性和保持文档格式不变的能力。然而,在某些情况下,我们可能需要知道合并到pdf。无论是为了方便管理、共享或者其他目的,本文将介绍…...

vue使用jsencrypt实现rsa前端加密
实现 RSA 加密 介绍 vue 完成 rsa 加密传输,jsencrypt 实现参数的前端加密 1 安装 jsencrypt npm install jsencrypt2 编写 jsencrypt.js 在 utils 文件夹中新建 jsencrypt.js 文件,内容如下:注意点:一般公钥都是后端生成好的&a…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
