(数字图像处理MATLAB+Python)第十二章图像编码-第一、二节:图像编码基本理论和无损编码
文章目录
- 一:图像编码基本理论
- (1)图像压缩的必要性
- (2)图像压缩的可能性
- A:编码冗余
- B:像素间冗余
- C:心理视觉冗余
- (3)图像压缩方法分类
- A:基于编码前后的信息保持程度的分类
- B:基于编码方法的分类
- C:其他方法
- (4)图像编码术语
- 二:图像的无损压缩编码
- (1)无损编码理论
- (2)霍夫曼编码
- A:概述
- B:程序
- (3)算数编码
- A:概述
- B:程序
- (4)LZW编码
- A:概述
- B:程序
一:图像编码基本理论
图像编码:一种将数字图像转换为压缩表示形式的过程。它的目标是减少图像数据的存储空间,并在传输或存储时减少带宽和存储需求、主要分为两类
- 无损压缩:尽可能地保留原始图像的所有信息,以实现无失真的压缩。其中最常见的算法之一是无损JPEG(JPEG-LS)编码,它使用类似于有损JPEG的离散余弦变换,但保留了所有细节
- 有损压缩:通过牺牲一些细节和图像质量来实现更高的压缩比。最常见的有损压缩算法之一是JPEG(Joint Photographic Experts Group)编码。JPEG使用离散余弦变换(DCT)将图像分成不同频率的频谱,并根据人眼对颜色和亮度的感知特性来降低高频细节。这样可以大幅减少图像的体积,但会引入一定程度的失真
(1)图像压缩的必要性
图像压缩的必要性:
- 存储空间的节省:原始数字图像通常占据大量的存储空间。通过压缩图像,可以有效地减少其所占用的存储空间。例如,一个高分辨率的彩色图像可能需要几百兆字节的存储空间,而通过压缩可以将其缩小到几十兆字节或更少
- 传输效率的提高:对于需要通过网络进行传输的图像,较大的图像文件会占用更多的带宽和传输时间。通过压缩图像,可以显著降低传输所需的带宽和时间成本。这对于在线图片分享、视频流媒体等应用非常重要
- 资源的优化利用:在诸如移动设备、无人机、监控摄像头等资源受限的环境中,压缩图像可以减少处理和传输所需的计算资源和能源消耗。这有助于延长设备的电池寿命、提高处理速度,并降低硬件成本
例如,一部90分钟的彩色电影,每秒放映24帧。把它数字化,每帧512´512像素,每像素的R、G、B三分量分别占8b,则总比特数为
90 × 60 × 24 × 3 × 512 × 512 × 8 b i t = 97 , 200 M B 90×60×24×3×512×512×8bit=97,200MB 90×60×24×3×512×512×8bit=97,200MB
因此,传输带宽、速度、存储器容量的限制使得对图象数据进行压缩显得非常必要

(2)图像压缩的可能性
A:编码冗余
编码冗余:称为信息熵冗余。如果一个图像的灰度级编码,使用了多于实际需要的编码符号,就称该图像包含了编码冗余\
例如下图,如果用8bit表示该图像的像素,那么则认为该图像存在编码冗余。因为该图像的像素只有两个灰度级,用1bit即可表示

在大多数图像中,图像像素的灰度值分布是不均匀的,因此若对图像的灰度值直接进行自然二进制编码(等长编码),则会对有最大和最小概率可能性的值分配相同比特数,而产生了编码冗余

用自然二进制编码时没有考虑像素灰度值出现的概率。只有按概率分配编码长度,才是最精减的编码方法。也即,灰度级出现概率大的用短码表示,出现概率小的灰度级用长码表示,则有可能使编码总长度下降

B:像素间冗余
像素间冗余:对应图像目标的像素之间一般具有相关性。因此,图像中一般存在与像素间相关性直接联系着的数据冗余——像素相关冗余。主要有
- 空间冗余:邻近像素灰度分布的相关性很强
- 频间冗余:多谱段图像中各谱段图像对应像素之间灰度相关性很强
- 时间冗余:序列图像帧间画面对应像素灰度的相关性很强
- 结构冗余:有些图像存在较强的纹理结构或自相似性,如墙纸、草席等图像
- 知识冗余:有些图像中包含与某些先验知识相关的信息

C:心理视觉冗余
心理视觉冗余:人的眼睛并不是对所有信息都有相同的敏感度,有些信息在通常的视觉感觉过程中与另外一些信息相比来说并不那么重要,这些信息可以认为是心理视觉冗余的
(3)图像压缩方法分类
A:基于编码前后的信息保持程度的分类
- 信息保持编码(无损编码): 在编解码过程中保证图像信息不丢失,通常压缩比一般不超过3:1
- 保真度编码(有损编码): 丢掉一些人眼不敏感的次要信息,在一定保真度准则下,最大限度地压缩图像
- 特征提取: 在图像识别、分析和分类等技术中,只对感兴趣部分特征进行编码压缩
B:基于编码方法的分类
- 熵编码: 基于信息统计特性的编码技术。如行程编码、Huffman编码和算术编码等
- 预测编码: 常用的有差分脉冲编码调制和运 动估计与补偿预测编码法
- 变换编码: 将空间域图像经过正交变换映射 到另一变换域上,再采用适当的量化和熵编码来有效压缩图像。通常采用的变换:离散傅里叶变换(DFT)、离散余弦变换(DCT)和离散小波变换(DWT)等
C:其他方法
-
早起编码方法:如混合编码、矢量量化、LZW算法等
-
一些新的编码方法
- 人工神经元网络ANN的压缩编码
- 分形编码
- 小波编码
- 基于模型的压缩编码
- 基于对象的压缩编码
- …
(4)图像编码术语
压缩比:
r = n L ˉ = 压缩前每像素所占平均比特数目 压后每像素所占平均比特数目 r=\frac{n}{\bar{L}}=\frac{\text { 压缩前每像素所占平均比特数目 }}{\text { 压后每像素所占平均比特数目 }} r=Lˉn= 压后每像素所占平均比特数目 压缩前每像素所占平均比特数目
图像熵:
- 令 p ( d i ) p(d_{i}) p(di)为数字图像第 i i i个灰度级 d i d_{i} di的出现概率
H = − ∑ i = 1 m p ( d i ) log 2 p ( d i ) ( p p i x e l / b i t ) H=-\sum_{i=1}^{m} p\left(d_{i}\right) \log _{2} p\left(d_{i}\right)\left(p^{p i x e l} /{ }_{b i t}\right) H=−i=1∑mp(di)log2p(di)(ppixel/bit)
平均码字长度 L ˉ \bar{L} Lˉ:
- 令 L i L_{i} Li为数字图像第 i i i个灰度级 d i d_{i} di的编码长度
L ˉ = ∑ i = 1 m L i p ( d i ) ( pixel / bit ) \bar{L}=\sum_{i=1}^{m} L_{i} p\left(d_{i}\right) \quad(\text { pixel } / \text { bit }) Lˉ=i=1∑mLip(di)( pixel / bit )
编码效率:
η = H L ˉ × 100 % \eta=\frac{H}{\bar{L}} \times 100 \% η=LˉH×100%
二:图像的无损压缩编码
(1)无损编码理论
Shannon无失真编码定理:也称为香农编码定理(Shannon’s source coding theorem),是信息论中的一个重要定理,由克劳德·香农(Claude Shannon)在1948年提出。该定理表明,在一给定离散概率分布下,对于任意平均码长小于熵的正数值,存在一种编码方式可以使得编码后的数据长度趋近于此平均码长,并且解码时不会引入任何失真。简而言之,香农无失真编码定理表明,对于具有确定概率分布的离散信源,我们可以设计一种编码方案,使得编码后的数据尽可能地紧凑,接近其熵值。在解码时,我们可以完全恢复原始的消息,没有任何信息的丢失或失真。这个定理在信息压缩领域具有重要的应用价值,它提供了一种理论基础和算法思路,用于有效地压缩数据并在解压缩时还原原始信息。同时,无失真编码定理也为其他信息论相关的研究和应用提供了重要参考和指导
如下,假设有一原始符号序列为
a 1 a 4 a 4 a 1 a 2 a 1 a 1 a 4 a 1 a 3 a 2 a 1 a 4 a 1 a 1 a_{1}a_{4}a_{4}a_{1}a_{2}a_{1}a_{1}a_{4}a_{1}a_{3}a_{2}a_{1}a_{4}a_{1}a_{1} a1a4a4a1a2a1a1a4a1a3a2a1a4a1a1
若采用等长编码,等长编码是将所有符号当作等概率事件处理的
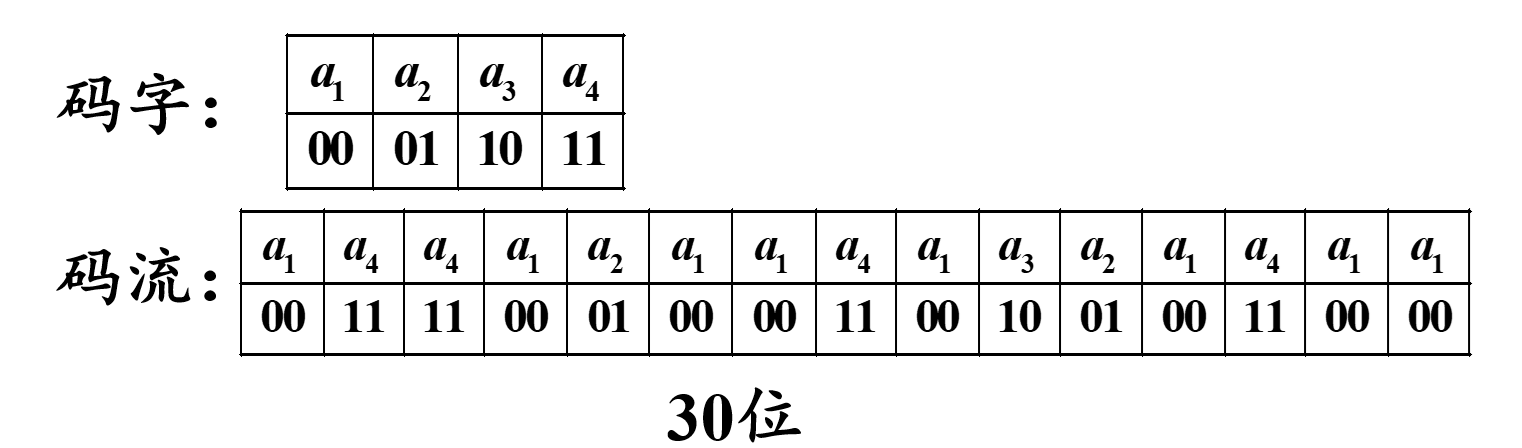
若采用变字长编码,变字长编码是每个符号的码字长度随字符出现概率而变化
- a 1 a_{1} a1:8次
- a 2 a_{2} a2:2次
- a 3 a_{3} a3:1次
- a 4 a_{4} a4:4次
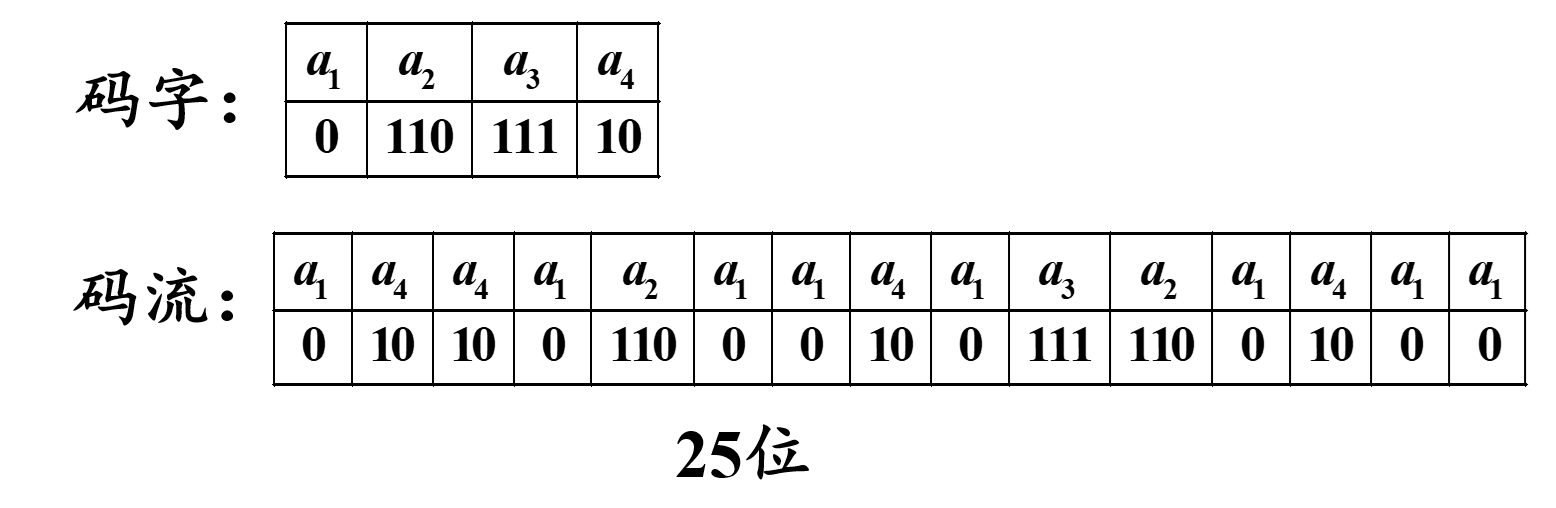
(2)霍夫曼编码
A:概述
此部分内容不在详细介绍,请移步(王道408考研数据结构)第五章树-第四节3:哈夫曼树基本概念、构造和哈夫曼编码
B:程序
实现图像的霍夫曼编码
matlab:
clc;clear;
%load image
Image=[7 2 5 1 4 7 5 0; 5 7 7 7 7 6 7 7; 2 7 7 5 7 7 5 4; 5 2 4 7 3 2 7 5;1 7 6 5 7 6 7 2; 3 3 7 3 5 7 4 1; 7 2 1 7 3 3 7 5; 0 3 7 5 7 2 7 4];
[h w]=size(Image); totalpixelnum=h*w;
len=max(Image(:))+1;
for graynum=1:lengray(graynum,1)=graynum-1;%将图像的灰度级统计在数组gray第一列
end
%将各个灰度出现的频数统计在数组histgram中
for graynum=1:lenhistgram(graynum)=0; gray(graynum,2)=0;for i=1:wfor j=1:hif gray(graynum,1)==Image(j,i)histgram(graynum)=histgram(graynum)+1;endendendhistgram(graynum)=histgram(graynum)/totalpixelnum;
end
histbackup=histgram;
%找到概率序列中最小的两个,相加,依次增加数组hist的维数,存放每一次的概率和,同时将原概率屏蔽(置为1.1);
%最小概率的序号存放在tree第一列中,次小的放在第二列
sum=0; treeindex=1;
while(1)if sum>=1.0break;else[sum1,p1]=min(histgram(1:len)); histgram(p1)=1.1;[sum2,p2]=min(histgram(1:len)); histgram(p2)=1.1;sum=sum1+sum2; len=len+1; histgram(len)=sum;tree(treeindex,1)=p1; tree(treeindex,2)=p2;treeindex=treeindex+1; end
end
%数组gray第一列表示灰度值,第二列表示编码码值,第三列表示编码的位数
for k=1:treeindex-1i=k; codevalue=1;if or(tree(k,1)<=graynum,tree(k,2)<=graynum)if tree(k,1)<=graynumgray(tree(k,1),2)=gray(tree(k,1),2)+codevalue;codelength=1;while(i<treeindex-1)codevalue=codevalue*2;for j=i:treeindex-1if tree(j,1)==i+graynumgray(tree(k,1),2)=gray(tree(k,1),2)+codevalue;codelength=codelength+1;i=j; break;elseif tree(j,2)==i+graynumcodelength=codelength+1;i=j; break;endendendgray(tree(k,1),3)=codelength;endi=k; codevalue=1;if tree(k,2)<=graynumcodelength=1;while(i<treeindex-1)codevalue=codevalue*2;for j=i:treeindex-1if tree(j,1)==i+graynumgray(tree(k,2),2)=gray(tree(k,2),2)+codevalue;codelength=codelength+1;i=j; break;elseif tree(j,2)==i+graynumcodelength=codelength+1;i=j; break;endendendgray(tree(k,2),3)=codelength;endend
end
%把gray数组的第二三列,即灰度的编码值及编码位数输出
for k=1:graynumA{k}=dec2bin(gray(k,2),gray(k,3));
end
disp('编码');
disp(A);python:
import numpy as np
import matplotlib.pyplot as plt# Load image
Image = np.array([[7, 2, 5, 1, 4, 7, 5, 0],[5, 7, 7, 7, 7, 6, 7, 7],[2, 7, 7, 5, 7, 7, 5, 4],[5, 2, 4, 7, 3, 2, 7, 5],[1, 7, 6, 5, 7, 6, 7, 2],[3, 3, 7, 3, 5, 7, 4, 1],[7, 2, 1, 7, 3, 3, 7, 5],[0, 3, 7, 5, 7, 2, 7, 4]])h, w = Image.shape
totalpixelnum = h * w
len = np.max(Image) + 1gray = np.zeros((len, 3))
gray[:, 0] = np.arange(len)histgram = np.zeros(len)
for graynum in range(len):histgram[graynum] = np.sum(Image == graynum) / totalpixelnumhistbackup = histgram.copy()sum_val = 0
treeindex = 0
tree = np.zeros((len, 2))
while True:if sum_val >= 1.0:breakelse:p1 = np.argmin(histgram)histgram[p1] = 1.1p2 = np.argmin(histgram)histgram[p2] = 1.1sum_val = histbackup[p1] + histbackup[p2]len += 1histgram[len-1] = sum_valtree[treeindex, 0] = p1tree[treeindex, 1] = p2treeindex += 1gray[:, 1] = np.arange(len)for k in range(treeindex):i = kcodevalue = 1if tree[k, 0] <= graynum or tree[k, 1] <= graynum:if tree[k, 0] <= graynum:gray[int(tree[k, 0]), 1] += codevaluecodelength = 1while i < treeindex - 1:codevalue *= 2for j in range(i, treeindex - 1):if tree[j, 0] == i + graynum:gray[int(tree[k, 0]), 1] += codevaluecodelength += 1i = jbreakelif tree[j, 1] == i + graynum:codelength += 1i = jbreakgray[int(tree[k, 0]), 2] = codelengthi = kcodevalue = 1if tree[k, 1] <= graynum:codelength = 1while i < treeindex - 1:codevalue *= 2for j in range(i, treeindex - 1):if tree[j, 0] == i + graynum:gray[int(tree[k, 1]), 1] += codevaluecodelength += 1i = jbreakelif tree[j, 1] == i + graynum:codelength += 1i = jbreakgray[int(tree[k, 1]), 2] = codelength# Convert gray code to binary strings
A = [bin(int(x[1]))[2:].zfill(int(x[2])) for x in gray[:len]]# Display the encoding
print("编码:")
for i, code in enumerate(A):print(f"{i}: {code}")# Plotting the image
plt.imshow(Image, cmap='gray')
plt.axis('off')
plt.show()(3)算数编码
A:概述
算数编码:是一种无失真的数据压缩技术,用于将源数据序列转换为更紧凑的编码序列。与传统的固定长度编码方法(如霍夫曼编码)不同,算术编码使用一个区间来表示整个源数据序列,而不是将每个符号映射到固定长度的编码字。算术编码的基本思想是利用符号出现的概率分布来为每个符号分配一个对应的区间,并根据输入的符号序列逐步缩小区间范围。最终,所生成的区间内的任意一个数值都可以表示原始数据序列的唯一编码。基本步骤如下
- 初始化:给定待编码的符号序列和对应的概率分布。
- 创建初始区间:根据符号的概率分布,为每个符号分配一个区间。
- 编码:根据每个输入符号,按照其在当前区间的长度比例,更新区间的上界和下界。
- 重标定:根据区间的更新,进行重标定以保证精度和避免溢出。
- 输出:当所有符号编码完成后,输出最终区间中的任意一个编码值作为压缩结果
算术编码的优势在于可以实现接近熵编码效率的压缩比,尤其适用于符号概率分布不均匀、频率较高的数据。然而,算术编码的实现相对复杂且计算量大,同时对解码过程中的精度要求较高。需要注意的是,由于算术编码涉及到浮点数运算和精度处理,因此在实际应用中可能存在一定的误差累积和舍入误差问题。这些问题可以通过使用更高精度的数值表示或采用其他技巧来缓解。总之,算术编码是一种强大的数据压缩技术,能够提供较高的压缩比,尤其适用于无损压缩和对压缩比要求较高的场景
B:程序
matlab:
%算术编码
clc;clear;
%load image
%Image=[7 2 5 1 4 7 5 0;5 7 7 7 7 6 7 7;2 7 7 5 7 7 5 4;5 2 4 7 3 2 7 5;
% 1 7 6 5 7 6 7 2;3 3 7 3 5 7 4 1;7 2 1 7 3 3 7 5;0 3 7 5 7 2 7 4];
Image=[4 1 3 1 2];
[h w col]=size(Image); pixelnum=h*w;
graynum=max(Image(:))+1;
for i=1:graynumgray(i)=i-1;
end
histgram=zeros(1,graynum);
for i=1:wfor j=1:hpixel=uint8(Image(j,i)+1);histgram(pixel)=histgram(pixel)+1; end
end
histgram=histgram/pixelnum;%将各个灰度出现的频数统计在数组histgram中
disp('灰度级');disp(num2str(gray));
disp('概率');disp(num2str(histgram))
disp('每一行字符串及其左右编码:')
for j=1:hstr=num2str(Image(j,:)); left=0; right=0;intervallen=1; len=length(str);for i=1:lenif str(i)==' 'continue;endm=str2num(str(i))+1; pl=0; pr=0;for j=1:m-1pl=pl+histgram(j);endfor j=1:mpr=pr+histgram(j);endright=left+intervallen*pr; left=left+intervallen*pl;%间隔区间起始和终止端点 intervallen=right-left; % 间隔区间宽度 end%输入图像信息数据disp(str); %编码输出间隔区间disp(num2str(left)); disp(num2str(right)) temp=0; a=1;while(1)left=2*left;right=2*right;if floor(left)~=floor(right)break;endtemp=temp+floor(left)*2^(-a);a=a+1;left=left-floor(left);right=right-floor(right);endtemp=temp+2^(-a);ll=a;%寻找最后区间内的最短二进制小数和所需的比特位数disp(num2str(temp)); disp(ll); %算术编码的编码码字输出:disp('算术编码的编码码字输出:'); %yy=DEC2bin(temp,ll);%简单的将10进制转化为N为2进制小数for ii= 1: lltemp1=temp*2;yy(ii)=floor(temp1);temp=temp1-floor(temp1);enddisp(num2str(yy));
endpython:
import numpy as np# 算术编码
# load image
Image = np.array([[4, 1, 3, 1, 2]])
[h, w] = Image.shape
pixelnum = h * w
graynum = np.max(Image) + 1gray = np.arange(graynum)histgram = np.zeros(graynum)
for i in range(w):for j in range(h):pixel = Image[j, i]histgram[pixel] += 1histgram /= pixelnum
print('灰度级:', gray)
print('概率:', histgram)print('每一行字符串及其左右编码:')
for j in range(h):str_ = [str(x) for x in Image[j]]left = 0right = 0intervallen = 1len_ = len(str_)for i in range(len_):if str_[i] == ' ':continuem = int(str_[i]) + 1pl = np.sum(histgram[:m-1])pr = np.sum(histgram[:m])right = left + intervallen * prleft = left + intervallen * plintervallen = right - leftprint(''.join(str_))print(left, right)temp = 0a = 1while True:left *= 2right *= 2if int(left) != int(right):breaktemp += int(left) * pow(2, -a)a += 1left -= int(left)right -= int(right)temp += pow(2, -a)ll = aprint(temp, ll)print('算术编码的编码码字输出:')yy = []for ii in range(ll):temp1 = temp * 2yy.append(int(temp1))temp = temp1 - int(temp1)print(yy)(4)LZW编码
A:概述
**LZW编码:是一种用于数据压缩的无损压缩算法,它可以将输入数据中的重复模式编码为更短的代码,从而减小数据的存储空间。LZW编码最初由Terry Welch在1984年提出,广泛应用于图像、音频和文本等领域。LZW编码的基本思想是利用字典来对输入数据进行编码。初始时,字典中包含所有可能的单个字符作为键,以及相应的编号作为值。然后,从输入数据的开头开始,逐步扫描输入数据,并检查当前扫描的序列是否已经在字典中存在。如果已存在,则继续向后扫描并将当前序列与下一个字符拼接,直到找到一个新的序列。此时,将该新序列的编号输出,并将这个新序列添加到字典中,以供后续的编码使用。整个过程持续进行,直到扫描完整个输入数据。LZW编码的关键是维护一个动态更新的字典。在编码过程中,字典不断增长,并根据输入数据中的模式进行更新。因此,相同的输入数据可以使用不同长度的编码表示,具有较高的压缩比
B:程序
matlab:
clc;clear;
Image=[30 30 30 30;110 110 110 110;30 30 30 30;110 110 110 110];
[h w col]=size(Image);
pixelnum=h*w; graynum=256;
%graynum=max(Image(:))+1;
if col==1 graystring=reshape(Image',1,pixelnum);%灰度图像从二维变为一维信号for tablenum=1:graynumtable{tablenum}=num2str(tablenum-1);endlen=length(graystring); lzwstring(1)=graynum;R=''; stringnum=1;for i=1:lenS=num2str(graystring(i));RS=[R,S]; flag=ismember(RS,table);if flagR=RS;elselzwstring(stringnum)=find(cellfun(@(x)strcmp(x,R),table))-1;stringnum=stringnum+1; tablenum=tablenum+1;table{tablenum}=RS; R=S;endendlzwstring(stringnum)=find(cellfun(@(x)strcmp(x,R),table))-1;disp('LZW码串: ')disp(lzwstring)
end
python:
import numpy as npImage = np.array([[30, 30, 30, 30],[110, 110, 110, 110],[30, 30, 30, 30],[110, 110, 110, 110]])[h, w] = Image.shape
pixelnum = h * w
graynum = 256if Image.ndim == 2:graystring = Image.T.flatten()table = {str(i): i for i in range(graynum)}lzwstring = [graynum]R = ''stringnum = 1for i in range(len(graystring)):S = str(graystring[i])RS = R + Sif RS in table:R = RSelse:lzwstring.append(table[R])stringnum += 1tablenum = len(table)table[RS] = tablenumR = Slzwstring.append(table[R])print('LZW码串:')print(lzwstring)相关文章:

(数字图像处理MATLAB+Python)第十二章图像编码-第一、二节:图像编码基本理论和无损编码
文章目录 一:图像编码基本理论(1)图像压缩的必要性(2)图像压缩的可能性A:编码冗余B:像素间冗余C:心理视觉冗余 (3)图像压缩方法分类A:基于编码前后…...

【Unity编辑器扩展】| 顶部菜单栏扩展 MenuItem
前言【Unity编辑器扩展】 | 顶部菜单栏扩展 MenuItem一、创建多级菜单二、创建可使用快捷键的菜单项三、调节菜单显示顺序和可选择性四、创建可被勾选的菜单项五、右键菜单扩展5.1 Hierarchy 右键菜单5.2 Project 右键菜单5.3 Inspector 组件右键菜单六、AddComponentMenu 特性…...

golang读取键盘功能按键输入
golang读取键盘功能按键输入 需求 最近业务上需要做一个终端工具,能够直接连到docker容器中进行交互。 技术选型 docker官方提供了python sdk、go sdk和remote api。 https://docs.docker.com/engine/api/sdk/ 因为我们需要提供命令行工具,因此采用g…...

用sklearn实现线性回归和岭回归
此文为ai创作,今天写文章的时候发现创作助手限时免费,想测试一下,于是就有了这篇文章,看的出来,效果还可以,一行没改。 线性回归 在sklearn中,可以使用线性回归模型做多变量回归。下面是一个示…...

结构型模式-桥接模式
用于把抽象化与实现化解耦,使得二者可以独立变化。这种类型的设计模式属于结构型模式,它通过提供抽象化和实现化之间的桥接结构,来实现二者的解耦。 这种模式涉及到一个作为桥接的接口,使得实体类的功能独立于接口实现类…...

缓存的放置时间和删除时间
缓存的放置时间和删除时间是指缓存中存储的数据的生命周期。这两个时间点非常重要,因为它们决定了缓存数据的有效期和何时应该从缓存中删除。 缓存的放置时间(Cache Put Time):这是指数据首次放入缓存的时间点。当数据被放入缓存时…...
内网穿透实战应用-如何通过内网穿透实现远程发送个人本地搭建的hMailServer的邮件服务
文章目录 1. 安装hMailServer2. 设置hMailServer3. 客户端安装添加账号4. 测试发送邮件5. 安装cpolar6. 创建公网地址7. 测试远程发送邮件8. 固定连接公网地址9. 测试固定远程地址发送邮件 hMailServer 是一个邮件服务器,通过它我们可以搭建自己的邮件服务,通过cpolar内网映射工…...
)
ensp基础命令大全(华为设备命令)
路漫漫其修远兮,吾将上下而求索 今天写一些曾经学习过的网络笔记,希望对您的学习有所帮助。 OSPF,BGP,IS-IS的命令笔记没有写上来,计划单独写,敬请期待,或者您可以在这个网站查查 : 万能查询网站 …...

thinkphp6 入门(4)--数据库操作 增删改查
一、设计数据库表 比如我新建了一个数据库表,名为test 二、配置数据库连接信息 本地测试 直接在.env中修改,不用去config/database.php中修改 正式环境 三、增删改查 引入Db库 use think\facade\Db; 假设新增的控制器路径为 app\test\control…...
MyBatisPlus 基础实现(一)
说明 创建一个最基本的MyBatisPlus项目,参考官网。 依赖 MyBatisPlus 依赖,最新版是:3.5.3.2 (截止2023-9-4)。 <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-bo…...
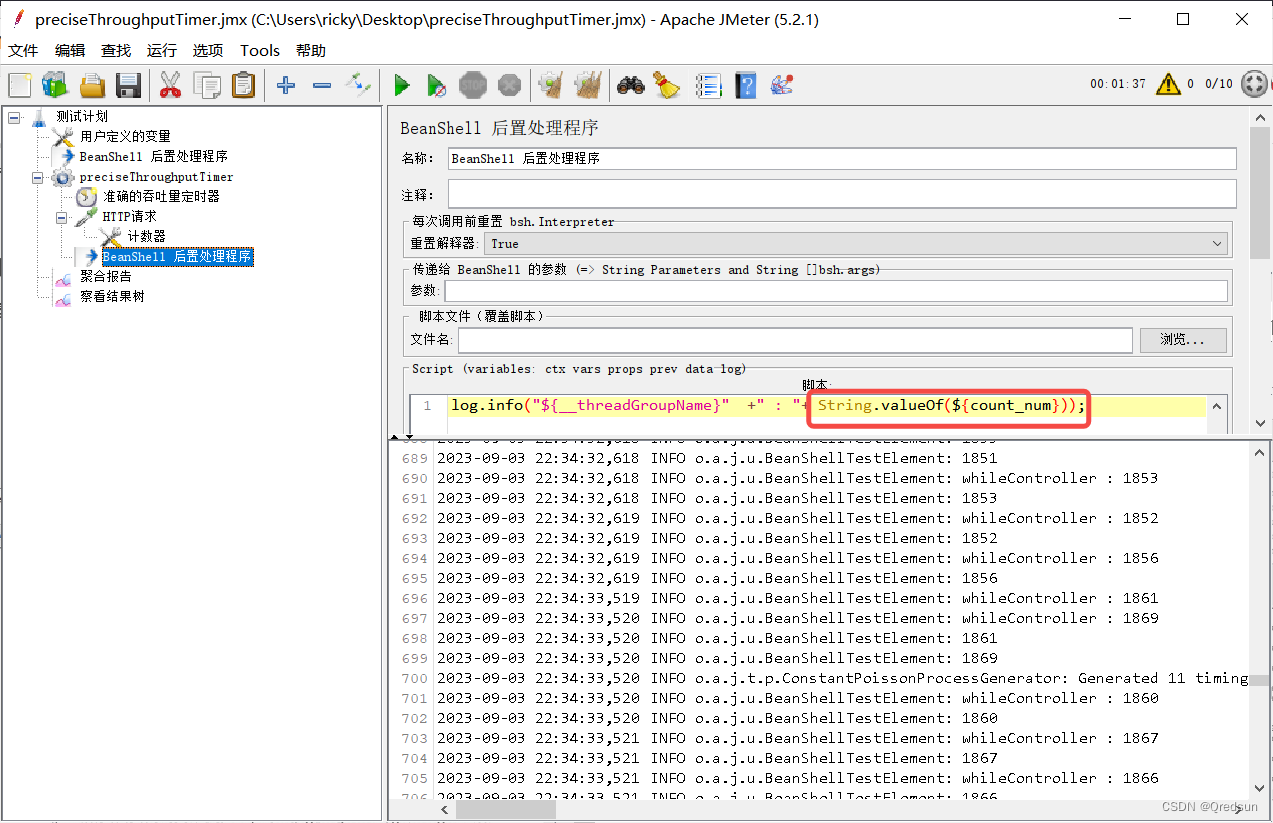
jmeter 计数器Counter
计数器可以用于生成动态的数值或字符串,以模拟不同的用户或数据。 计数器通常与用户线程组结合使用,以生成不同的变量值并在测试中应用。以下是计数器的几个常用属性: 变量前缀(Variable Name Prefix):定义…...
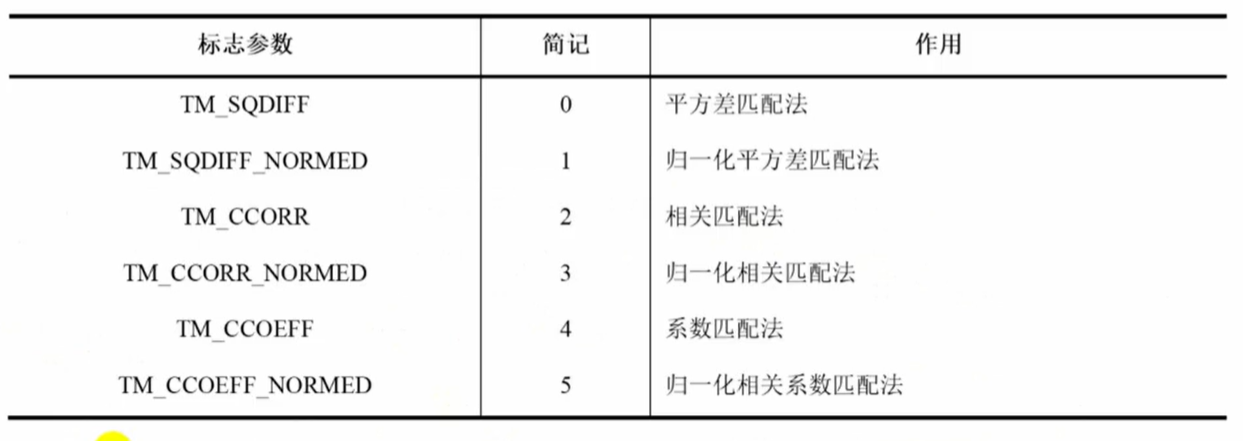
OpenCV(十九):模板匹配
1.模板匹配: OpenCV提供了一个模板匹配函数,用于在图像中寻找给定模板的匹配位置。 2.图像模板匹配函数matchTemplate void matchTemplate( InputArray image, InputArray templ, OutputArray result, int method, InputArray mask noArray() ); image…...
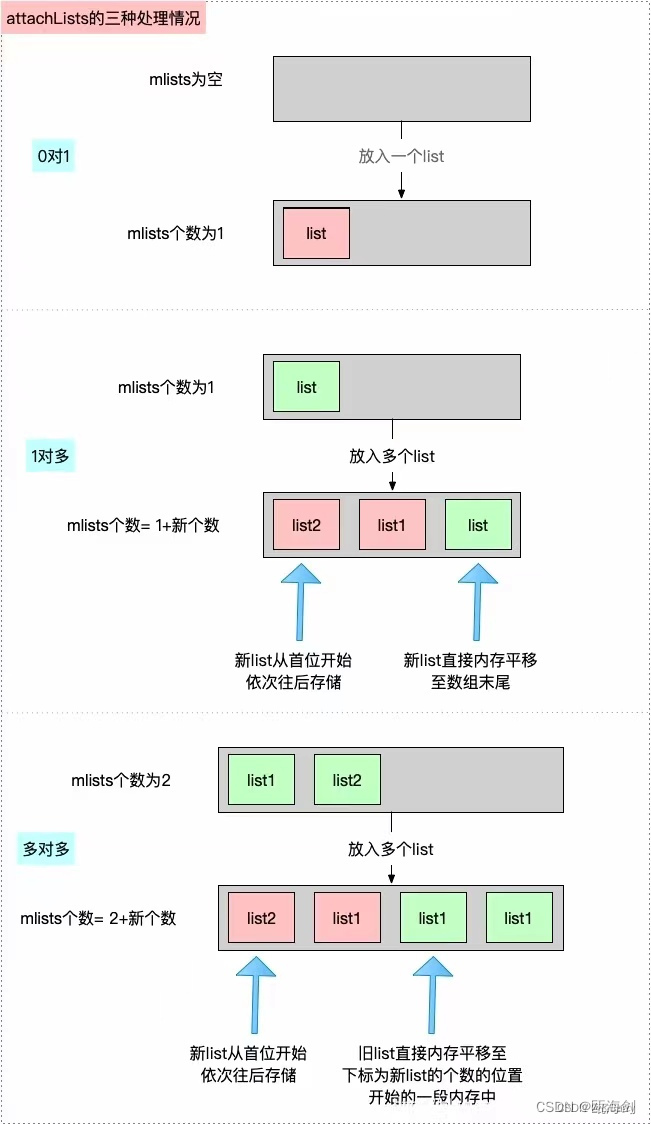
【iOS】Category、Extension和关联对象
Category分类 Category 是 比继承更为简洁 的方法来对Class进行扩展,无需创建子类就可以为现有的类动态添加方法。 可以给项目内任何已经存在的类 添加 Category甚至可以是系统库/闭源库等只暴露了声明文件的类 添加 Category (看不到.m 文件的类)通过 Category 可以添加 实例…...
)
支持向量机(一)
文章目录 前言分析数据集线性可分情况下的支持向量机原始问题凸优化包解法对偶问题凸优化包解法 数据集线性不可分情况下的线性支持向量机与软间隔最大化 前言 在支持向量机中,理论逻辑很简单:最大化最小的几何间隔。但是实际编写代码过程中有一个小点需…...

MyBatis中至关重要的关系映射----全方面介绍
目录 一 对于映射的概念 1.1 三种关系映射 1.2 resultType与resultMap的区别 resultType: resultMap: 二,一对一关联查询 2.1 嵌套结果集编写 2.2 案例演示 三,一对多关联查询 3.1 嵌套结果集编写 3.3 案例演示 四&…...
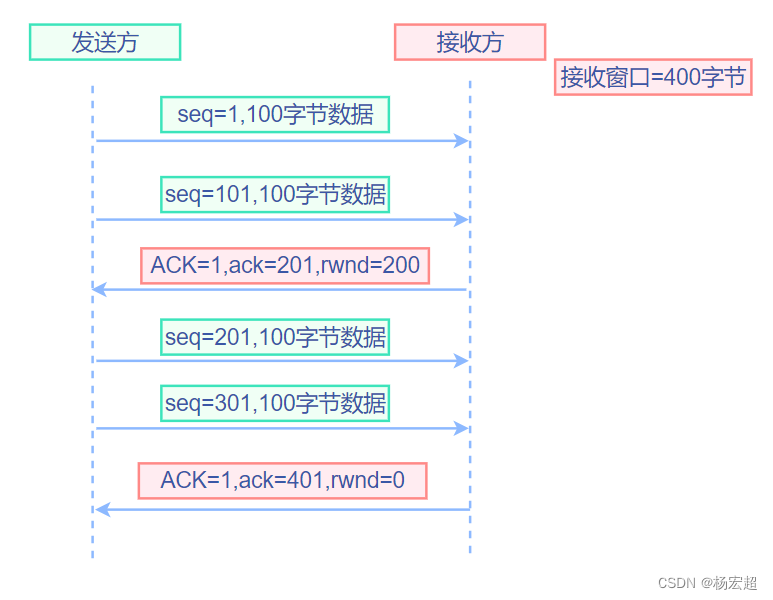
47、TCP的流量控制
从这一节开始,我们学习通信双方应用进程建立TCP连接之后,数据传输过程中,TCP有哪些机制保证传输可靠性的。本节先学习第一种机制:流量控制。 窗口与流量控制 首先,我们要知道的是:什么是流量控制ÿ…...
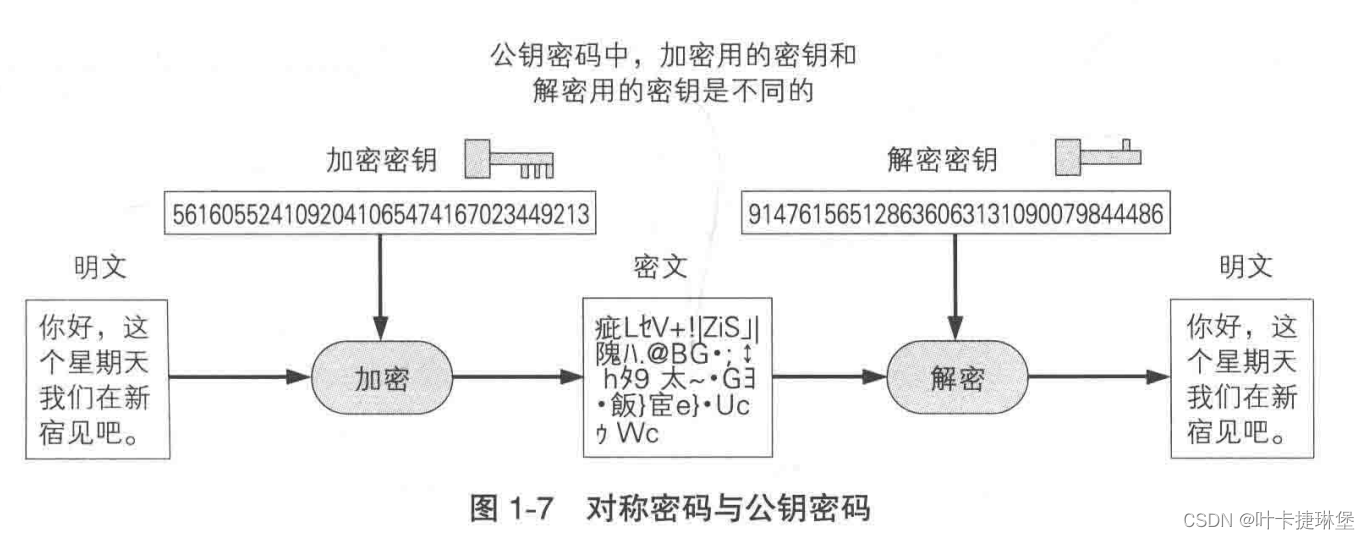
密码学入门——环游密码世界
文章目录 参考书目一、基本概念1.1 本书主要角色1.2 加密与解密 二、对称密码与公钥密码2.1 密钥2.2 对称密码和公钥密码2.3 混合密码技术 三、其他密码技术 参考书目 图解密码技术 第三版 一、基本概念 1.1 本书主要角色 1.2 加密与解密 加密 解密 密码破译 二、对称密…...
笔记本家庭版本win11上win+r,运行cmd默认没有管理员权限,如何调整为有管理员权限的
华为matebookeGo 笔记本之前有段时间不知怎么回事,打开运行框,没有了那一行“使用管理权限创建此任务”,而且cmd也不再是默认的管理员下的,这很不方便,虽然每次winr ,输入cmd后可以按ctrlshitenter以管理员权限运行&am…...

MavenCentral库发布记录
最近发布了 Android 路由库 URouter,支持 AGP8、ActivityResult启动等特性。 把提交到 Maven Central 过程记录一下。 一、注册 Sonatype 账号,新建项目 注册 https://issues.sonatype.org 登录后,新建项目: 相关选项&…...
的使用)
小程序进阶-env(safe-area-inset-bottom)的使用
一、简介 env(safe-area-inset-bottom)和env(safe-area-inset-top)是CSS中的变量,用于获取设备底部和顶部安全区域的大小。 所谓的安全区域就是指在iPhone X及以上的设备中,为避免被屏幕的“刘海”和“Home Indicator”所遮挡或者覆盖的有效区域区域&am…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
