2023牛客暑期多校训练营7 CI「位运算」「根号分治+容斥」
C-Beautiful Sequence_2023牛客暑期多校训练营7 (nowcoder.com)
题意:
给定一个b序列,a序列满足 a [ i − 1 ] < = a [ i ] a[i-1]<=a[i] a[i−1]<=a[i]且 a [ i ] ⊕ a [ i + 1 ] = b [ i ] a[i]\oplus a[i+1]=b[i] a[i]⊕a[i+1]=b[i],求字典序第k大的满足条件的a序列,若不存在则输出-1。
思路:
我们对b数组求一个
前缀和可以发现:p r e [ 1 ] = 0 ⊕ b [ 1 ] = a [ 1 ] ⊕ a [ 2 ] pre[1]=0\oplus b[1]=a[1]\oplus a[2] pre[1]=0⊕b[1]=a[1]⊕a[2]
p r e [ 2 ] = p r e [ 1 ] ⊕ b [ 2 ] = a [ 1 ] ⊕ a [ 2 ] ⊕ a [ 2 ] ⊕ a [ 3 ] = a [ 1 ] ⊕ a [ 3 ] pre[2]=pre[1]\oplus b[2]=a[1]\oplus a[2]\oplus a[2]\oplus a[3]=a[1]\oplus a[3] pre[2]=pre[1]⊕b[2]=a[1]⊕a[2]⊕a[2]⊕a[3]=a[1]⊕a[3]
……
依次类推,可以发现 p r e [ i ] = a [ 1 ] ⊕ a [ i + 1 ] pre[i]=a[1]\oplus a[i+1] pre[i]=a[1]⊕a[i+1],对于每一组 p r e [ i ] pre[i] pre[i]和 p r e [ i + 1 ] pre[i+1] pre[i+1],考虑二进制从最高位开始查询,当某一位不同的时候一定是因为 a [ i + 1 ] a[i+1] a[i+1]的这位为1而 a [ i ] a[i] a[i]的这位为0,于是我们可以确定 a [ 1 ] a[1] a[1]的某一位,遍历完成后会发现可能有一部分位置(sum)的值并未确定,所以所有可能的a序列就有 1 < < s u m 1<<sum 1<<sum个,而字典序第k大的就是 a [ 1 ] a[1] a[1]的取值为第k大的,确定 a [ 1 ] a[1] a[1]后即可通过b数组求得答案。
AC代码:
#include <bits/stdc++.h>
using namespace std;
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;
#define int ll
#define pb push_back
#define eb emplace_back
#define m_p make_pair
const int mod = 998244353;
#define mem(a,b) memset(a,b,sizeof a)
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 1e6 + 50;
//__builtin_ctzll(x);后导0的个数
//__builtin_popcount计算二进制中1的个数
ll a[N],b[N],pre[N];
int numa[33];void work() {int n,k;cin>>n>>k;pre[0]=0;a[1]=0;for(int i=1;i<n;++i){cin>>b[i];pre[i]=pre[i-1]^b[i];}for(int i=0;i<=30;++i)numa[i]=-1;for(int i=n-1;i>=1;--i){for(int j=30;j>=0;--j){if(((pre[i]>>j)&1)!=((pre[i-1]>>j)&1)){numa[j]=((pre[i-1]>>j)&1);break;}}}ll num=0;for(int i=0;i<30;++i){if(numa[i]==-1)num++;}if((1<<num)<k){cout<<"-1\n";return;}k--;for(int i=30;i>=0;--i){if(numa[i]==-1){if((k>>num)&1) numa[i]=1;else numa[i]=0;num--;}}ll x=1;for(int i=0;i<=30;++i){if(numa[i]==1)a[1]+=x;x*=2;}for(int i=2;i<=n;++i){a[i]=a[i-1]^b[i-1];if(a[i]<a[i-1]){cout<<"-1\n";return;}}for(int i=1;i<=n;++i){cout<<a[i]<<" \n"[i==n];}
}signed main() {io;int t=1;cin >> t;while (t--) {work();}return 0;
}
I-We Love Strings_2023牛客暑期多校训练营7 (nowcoder.com)
题意:
给定n个01?字串,其中?可以是0也可以是1,询问有多少个01字串符合至少一个给定的正则串。
思路:
根号分治。
在字串长小于20( s q r t ( 400 ) sqrt(400) sqrt(400))时dfs暴力找,总复杂度不会超过 2 21 2^{21} 221。
大于20时,容斥:
奇加偶减。
AC代码:
#include <bits/stdc++.h>
using namespace std;
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;
#define int ll
#define pb push_back
#define eb emplace_back
#define m_p make_pair
const int mod = 998244353;
#define mem(a,b) memset(a,b,sizeof a)
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const ll N = 405;
//__builtin_ctzll(x);后导0的个数
//__builtin_popcount计算二进制中1的个数
ll ans=0;
vector<string>a[N];
string tmp;
int n;void small(int now,int len){if (now==len+1){for(auto x:a[len]){bool ok=1;for(int j=0;j<len;j++) {if(x[j]=='?') continue;if(x[j]!=tmp[j]){ok=0;break;}}if (ok) {ans++;break;}}return ;}tmp+='0';small(now+1,len);tmp.pop_back();tmp+='1';small(now+1,len);tmp.pop_back();
}void big(int len,int size){ll m=1<<size;//正则串随意组合的情况数for(int i=1;i<m;++i){//枚举所有可能int cnt=0,ok=1;tmp.clear();for(int j=0;j<len;++j)tmp+="?";for(int j=0;j<size;++j){//枚举每种正则串的组合方式if(i>>j&1){cnt++;for(int t=0;t<len;++t){//枚举每一位char x=a[len][j][t];if(tmp[t]=='?'){tmp[t]=x;}else if(x!='?'&&tmp[t]!=x){ok=0;break;}}if(!ok)break;}}if(!ok)continue;int p=1;for(int j=0;j<len;++j){if(tmp[j]=='?')p=p*2%mod;//计算有多少个未确定的字符,每个未确定代表两种可能}if(cnt&1){ans=(ans+p)%mod;}else ans=(ans-p)%mod;}
}void work() {cin>>n;for(int i=1;i<=n;++i){string s;cin>>s;a[s.size()].pb(s);}for(int i=1;i<N;++i){if(!a[i].size()){continue;}if(i<=20){tmp.clear();small(1,i);}else{big(i,a[i].size());}}ans%=mod;cout<<ans<<'\n';
}signed main() {io;int t=1;//cin >> t;while (t--) {work();}return 0;
}
相关文章:

2023牛客暑期多校训练营7 CI「位运算」「根号分治+容斥」
C-Beautiful Sequence_2023牛客暑期多校训练营7 (nowcoder.com) 题意: 给定一个b序列,a序列满足 a [ i − 1 ] < a [ i ] a[i-1]<a[i] a[i−1]<a[i]且 a [ i ] ⊕ a [ i 1 ] b [ i ] a[i]\oplus a[i1]b[i] a[i]⊕a[i1]b[i],求字…...

YOLOv5算法改进(10)— 替换主干网络之GhostNet
前言:Hello大家好,我是小哥谈。GhostNet是一种针对计算机视觉任务的深度神经网络架构,它于2020年由中国科学院大学的研究人员提出。GhostNet的设计目标是在保持高精度的同时,减少模型的计算和存储成本。GhostNet通过引入Ghost模块…...

Android Canvas的使用
android.graphics.Canvas 一般在自定义View中,重写 onDraw(Canvas canvas) 方法时用到。 /*** Implement this to do your drawing.** param canvas the canvas on which the background will be drawn*/Overrideprotected void onDraw(Canvas canvas) {super.onDra…...
)
AI批量写文章伪原创:基于ChatGPT长文本模型,实现批量改写文章、批量回答问题(长期更新)
import traceback import openai import osopenai.api_key = ""conversation=[{"role": "system", "content": "You are a helpful assistant."}] max_history_len = 20 first_message = Nonedir = rJ:\ai\input #要改写的文…...

git常用场景记录 | 拉取远程分支A合并到本地分支B - 删除上一次的commit
文章目录 git常用场景记录拉取远程分支A合并到本地分支B本地分支B存在未add与commit的代码 删除上一次的commit已经push到远程库 git常用场景记录 doing,最后更新9.5 拉取远程分支A合并到本地分支B 需求描述 在团队合作时,我自己的本地分支B功能已经实现…...
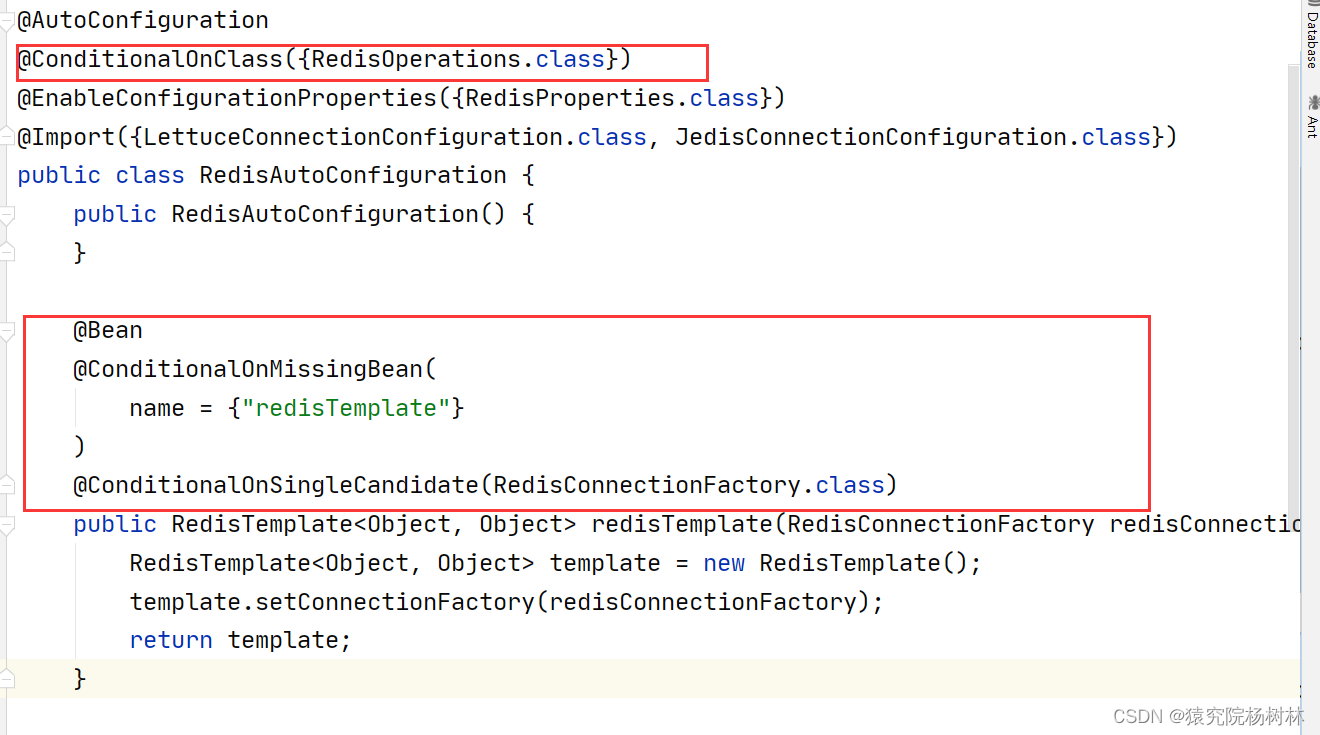
源码角度解析SpringBoot 自动配置
文章目录 前言一、了解相关注解1.Condition注解2.Enable注解 二、SpringBoot自动配置1.SpringBootApplication注解2.SpringBootConfiguration注解3.EnableAutoConfiguration注解4.Conditional注解 总结 前言 Spring Boot 自动配置是 Spring Boot 的核心特性之一,它…...

【原创】H3C路由器OSPF测试
网络拓扑图 路由器配置: 路由器1上接了4跟线,分别为这四个接口配置IP地址。 # interface GigabitEthernet0/0/0port link-mode routecombo enable copperip address 2.1.1.2 255.255.255.0 # interface GigabitEthernet0/0/1port link-mode routecombo…...

计算机视觉:轨迹预测综述
计算机视觉:轨迹预测综述 轨迹预测的定义轨迹预测的分类基于物理的方法(Physics-based)基于机器学习的方法(Classic Machine Learning-based)基于深度学习的方法(Deep Learning-based)基于强化学…...

三维跨孔电磁波CT数据可视化框架搭建
三维跨孔电磁波CT数据可视化框架搭建 文章目录 三维跨孔电磁波CT数据可视化框架搭建1、三维CT可视化结果2、matlab代码2.1、CT数据格式整理并保存2.2、三维可视化 利用matlab实现对跨孔电磁波CT实测数据反演,并搭建了三维CT数据可视化框架,可装填实测CT反…...

OC和Swift混编,导入头文件‘xxx-Swift.h‘ file not found
在OC的项目里加入Swift代码,创建完桥接文件后,需要倒入Swift头文件,头文件的格式为“项目名-Swift.h”。 如下图,我在Xcode上看到我的项目名为YichangPark,导入 #import "YiChangPark-Swift.h" 之后提示 “Y…...

一文读懂HOOPS Native平台:快速开发桌面端、移动端3D应用程序!
HOOPS Native Platform是用于在桌面和移动平台以及混合现实应用程序上构建3D工程应用程序的首要工具包。它由三个集成良好的软件开发工具包(SDK)组成:HOOPS Visualize、HOOPS Exchange、HOOPS Publish。HOOPS Visualize 是一个强大的图形引擎,适用于本机…...
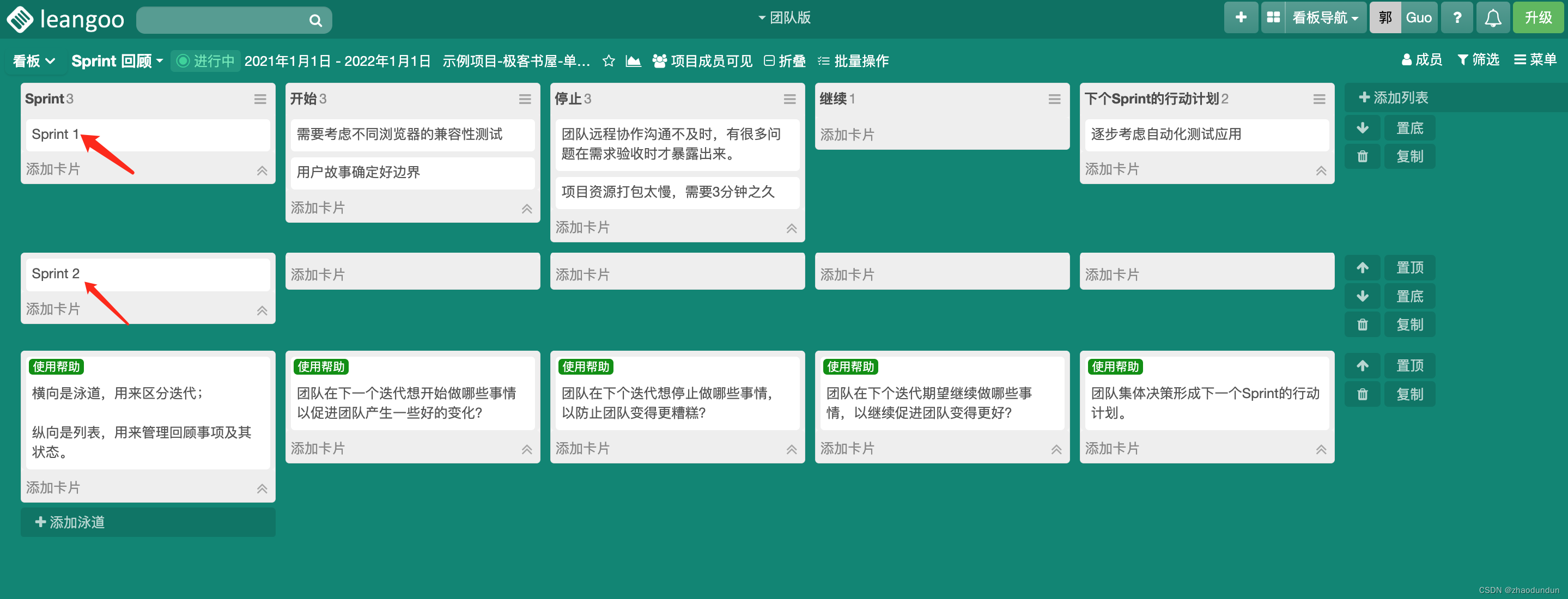
Scrum工作模式及Scrum工具
Scrum工作模式是一种敏捷软件开发方法,其核心是团队合作和自我组织,旨在通过短周期的迭代开发,实现快速反馈和持续改进。 Scrum工作模式包括以下角色和活动: 1、产品负责人(Product Owner):负…...
[ros][ubuntu]ros在ubuntu18.04上工作空间创建和发布一个话题
构建catkin工作空间 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src catkin_init_workspace cd ~/catkin_ws/ catkin_make 配置环境变量 echo "source ~/catkin_ws/devel/setup.bash" >> ~/.bashrc source ~/.bashrc 检查环境变量 echo $ROS_PACKAGE_PATH…...

我的区块链笔记
区块链 中心化的账本,个人节点和中心节点的地位不对等,中心节点说了算。去中心化,个人节点就是公平的,根据一套规则,叫做公比机制。 区块链的本质,就是数据存储方式 区块链使用密码学算法产生的区块&…...

Spring事务(ACID特性、隔离级别、传播机制、失效场景)
一、事务的ACID特性 原子性(Atomicity) 原子性是指事务是一个不可分割的工作单位,事务中的操作要么都发生,要么都不发生。一致性(Consistency) 事务前后数据的完整性必须保持一致。隔离性(Isola…...

机器学习笔记之最优化理论与方法(六)无约束优化问题——最优性条件
机器学习笔记之最优化理论与方法——无约束优化问题[最优性条件] 引言无约束优化问题无约束优化问题最优解的定义 无约束优化问题的最优性条件无约束优化问题的充要条件无约束优化问题的必要条件无约束优化问题的充分条件 引言 本节将介绍无约束优化问题,主要介绍无…...

E5061B/是德科技keysight E5061B网络分析仪
181/2461/8938产品概述 是德科技E5061B(安捷伦)网络分析仪在从5 Hz到3 GHz的宽频率范围内提供通用的高性能网络分析。E5061B提供ENA系列常见的出色RF性能,还提供全面的LF(低频)网络测量能力;包括内置1 Mohm输入的增益相位测试端口。E5061B从低频到高频的…...
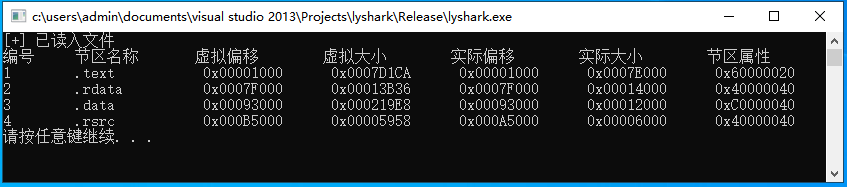
2.4 PE结构:节表详细解析
节表(Section Table)是Windows PE/COFF格式的可执行文件中一个非常重要的数据结构,它记录了各个代码段、数据段、资源段、重定向表等在文件中的位置和大小信息,是操作系统加载文件时根据节表来进行各个段的映射和初始化的重要依据…...
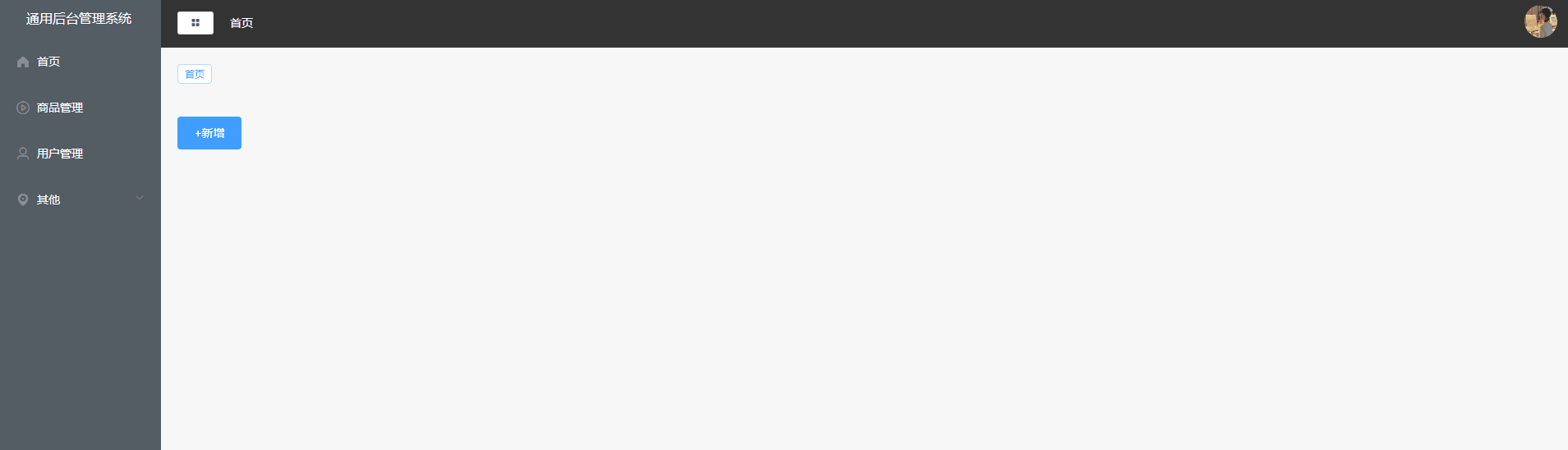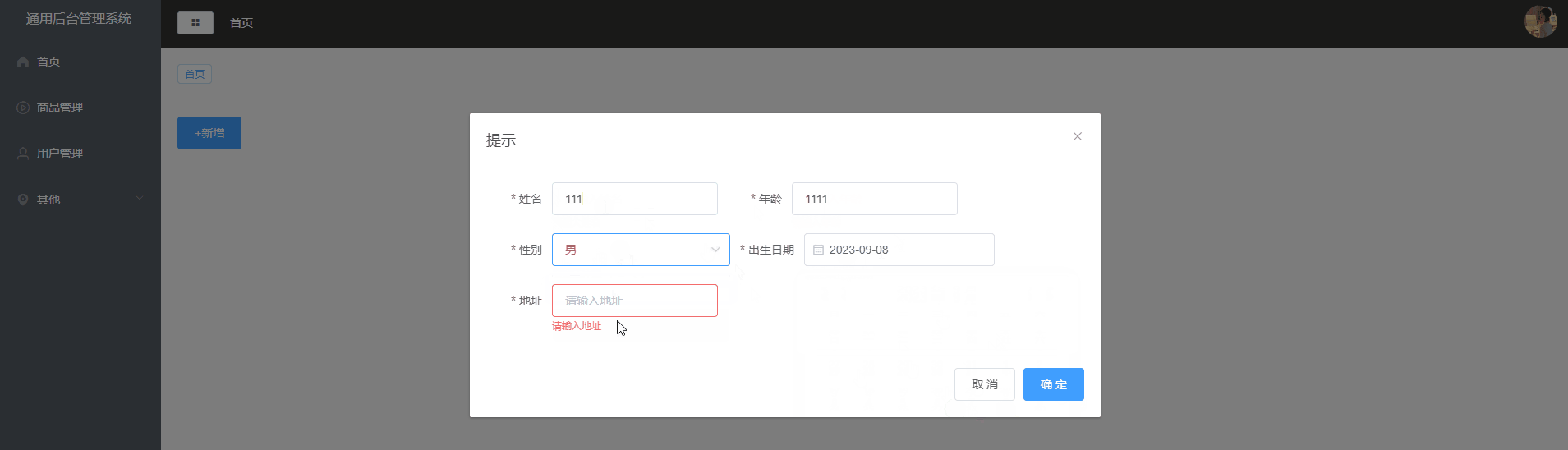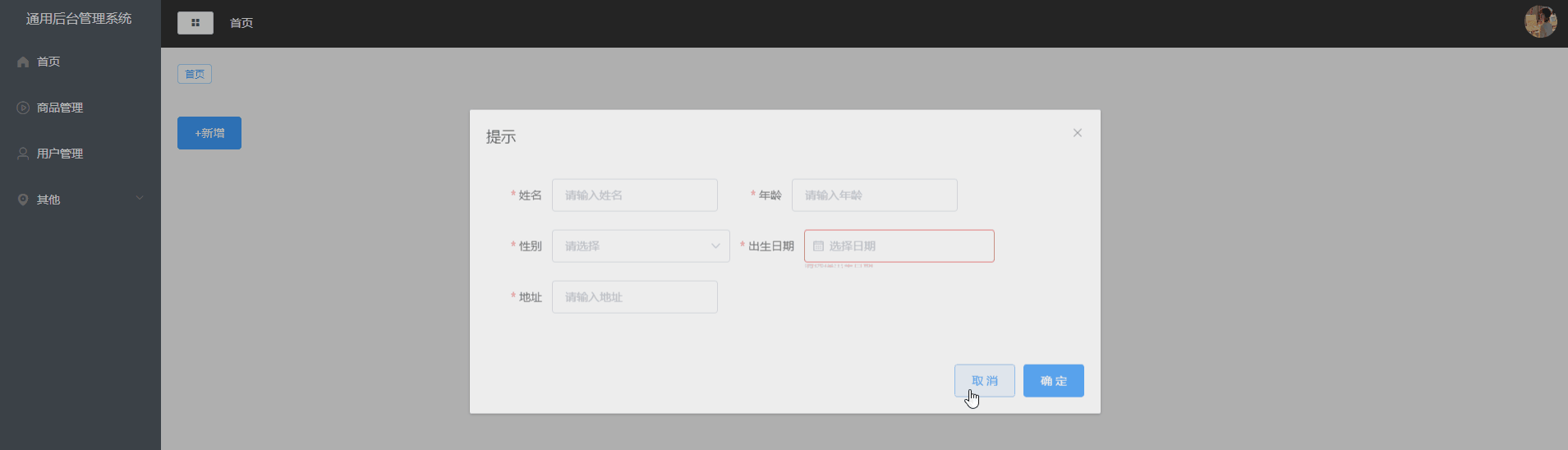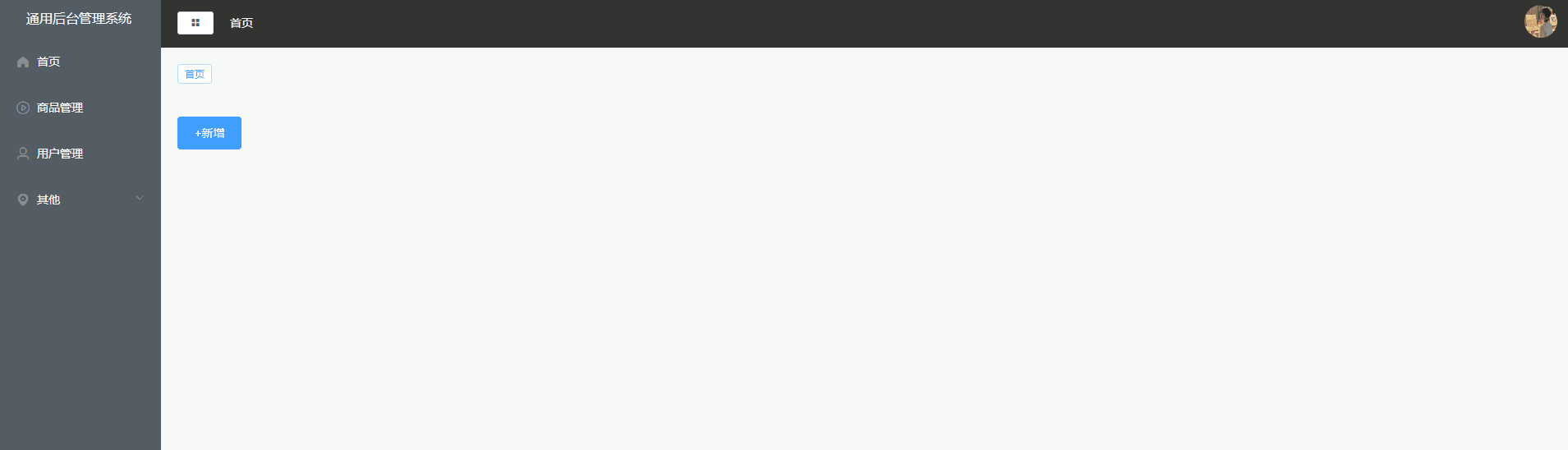
Vue2项目练手——通用后台管理项目第五节
Vue2项目练手——通用后台管理项目 首页组件布局面包屑&tag面包屑使用组件使用vuex存储面包屑数据src/store/tab.jssrc/components/CommonAside.vuesrc/components/CommonHeader.vue tag使用组件文件目录CommonTag.vueMain.vuetabs.js 用户管理页新增功能使用的组件页面布局…...

软件工程学术顶会——ESEC/FSE 2022 议题(网络安全方向)清单、摘要与总结
总结 本次会议中网络安全相关议题涵盖区块链、智能合约、符号执行、浏览器API模糊测试等不同研究领域。 热门研究方向: 1. 基于深度学习的漏洞检测与修复 2. 基于AI的自动漏洞修复 3. 模糊测试与漏洞发现 冷门研究方向: 1. 多语言代码的漏洞分析 2. 代码审查中的软件安全 3. 浏…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...
