机器学习笔记之最优化理论与方法(六)无约束优化问题——最优性条件
机器学习笔记之最优化理论与方法——无约束优化问题[最优性条件]
- 引言
- 无约束优化问题
- 无约束优化问题最优解的定义
- 无约束优化问题的最优性条件
- 无约束优化问题的充要条件
- 无约束优化问题的必要条件
- 无约束优化问题的充分条件
引言
本节将介绍无约束优化问题,主要介绍无约束优化问题最优解的相关性质。
本节是关于以优化算法——无约束算法概述为首,优化算法——线搜索方法(二~九)的理论补充。
无约束优化问题
无约束优化问题的数学符号表示如下:
仅需要对目标函数进行最小化,没有可行域的条件限制。
min f ( x ) \min f(x) minf(x)
在实际问题中,很多问题可以被建模成无约束优化问题。例如:线性回归方法中的最小二乘估计问题。对应数学符号表示如下:
很明显,最小二乘函数 ∥ A x − b ∥ 2 2 \|\mathcal A x - b\|_2^2 ∥Ax−b∥22明显是一个凸函数:其二次型系数矩阵 A T A \mathcal A^T\mathcal A ATA必然是半正定矩阵。
f ( x ) = ∥ A x − b ∥ 2 2 = ( A x − b ) T ( A x − b ) = x T [ A T A ] x + b T A x − x T A T b + b T b \begin{aligned} f(x) & = \|\mathcal Ax - b\|_2^2 \\ & = (\mathcal Ax - b)^T(\mathcal Ax - b) \\ & = x^T [\mathcal A^T\mathcal A] x + b^T \mathcal A x - x^T \mathcal A^T b + b^Tb \end{aligned} f(x)=∥Ax−b∥22=(Ax−b)T(Ax−b)=xT[ATA]x+bTAx−xTATb+bTb
因而该问题可以更精确地描述为无约束凸优化问题。
min ∥ A x − b ∥ 2 2 \min \|\mathcal A x - b\|_2^2 min∥Ax−b∥22
可以采用适当方法将约束优化问题转换为无约束优化问题。例如最优化问题概述中提到的罚函数法。
无约束优化问题最优解的定义
- 局部最优解 :假设 x ˉ \bar{x} xˉ是关于目标函数 f ( ⋅ ) f(\cdot) f(⋅)无约束优化问题的局部最优解,对于 ∀ x ∈ N ϵ ( x ˉ ) \forall x \in \mathcal N_\epsilon(\bar{x}) ∀x∈Nϵ(xˉ),必然有:
其中N ϵ ( x ˉ ) \mathcal N_{\epsilon}(\bar{x}) Nϵ(xˉ)表示包含点x ˉ \bar{x} xˉ,并且使用ϵ \epsilon ϵ表示范围的邻域。例如:( x ˉ − ϵ , x ˉ + ϵ ) (\bar{x} - \epsilon,\bar{x} + \epsilon) (xˉ−ϵ,xˉ+ϵ)
f ( x ) ≥ f ( x ˉ ) f(x) \geq f(\bar{x}) f(x)≥f(xˉ) - 全局最优解:相比于局部最优解,假设 x ∗ x^* x∗是关于目标函数 f ( ⋅ ) f(\cdot) f(⋅)无约束优化问题的全局最优解,对于 ∀ x ∈ R n \forall x \in \mathbb R^n ∀x∈Rn,必然有:
f ( x ) ≥ f ( x ∗ ) f(x) \geq f(x^*) f(x)≥f(x∗) - 严格最优解:与凸函数:定义与基本性质中提到的严格凸函数类似,其核心是消除掉取等的情况。关于严格最优解,同样可以分为严格局部最优解与严格全局最优解。对应数学符号表示如下:
{ ∀ x ∈ R n , x ≠ x ∗ ⇒ f ( x ) > f ( x ∗ ) ∀ x ∈ N ϵ ( x ˉ ) , x ≠ x ˉ ⇒ f ( x ) > f ( x ˉ ) \begin{cases} \forall x \in \mathbb R^n,x \neq x^* \Rightarrow f(x) > f(x^*) \\ \forall x \in \mathcal N_{\epsilon}(\bar{x}), x \neq \bar{x} \Rightarrow f(x) > f(\bar{x}) \end{cases} {∀x∈Rn,x=x∗⇒f(x)>f(x∗)∀x∈Nϵ(xˉ),x=xˉ⇒f(x)>f(xˉ)
对应图像表示如下:

根据凸函数的定义可以看出, f ( ⋅ ) , G ( ⋅ ) f(\cdot),\mathcal G(\cdot) f(⋅),G(⋅)都是凸函数。其中 f ( ⋅ ) f(\cdot) f(⋅)中描述的红色点是严格最优解;而红色点 G ( x ∗ ) \mathcal G(x^*) G(x∗)是最优解的条件下, ∃ x ≠ x ∗ ⇒ f ( x ) = f ( x ∗ ) \exist x \neq x^* \Rightarrow f(x) = f(x^*) ∃x=x∗⇒f(x)=f(x∗)。那么该函数的最优解不是严格最优解。
无约束优化问题的最优性条件
针对无约束优化问题 ⇒ min f ( x ) \Rightarrow \min f(x) ⇒minf(x):
无约束优化问题的充要条件
如果目标函数 f ( x ) f(x) f(x)是凸函数,则存在如下等价条件:
关于无约束凸优化问题,详细解释见最优化理论与方法——凸优化问题(上),这里不再赘述。
x ∗ is Optimal ⇔ ∇ f ( x ∗ ) = 0 x^* \text{ is Optimal } \Leftrightarrow \nabla f(x^*) = 0 x∗ is Optimal ⇔∇f(x∗)=0
无约束优化问题的必要条件
如果目标函数 f ( x ) f(x) f(x)不是凸函数,只是一般函数,上述的充要条件不一定成立,但一定满足如下必要条件:
如果x ∗ x^* x∗是最优解,那么它一定是平稳点;如果f ( ⋅ ) f(\cdot) f(⋅)在x ∗ x^* x∗位置的Hessian Matrix ⇒ ∇ 2 f ( x ∗ ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(x^*) Hessian Matrix⇒∇2f(x∗)存在,那么该矩阵至少是半正定矩阵;如果将f ( ⋅ ) f(\cdot) f(⋅)退化成一元函数,必然有:f ′ ′ ( x ∗ ) ≥ 0 f''(x^*) \geq 0 f′′(x∗)≥0。
x ∗ is Optimal ⇒ { ∇ f ( x ∗ ) = 0 ∇ 2 f ( x ∗ ) ≽ 0 x^* \text{ is Optimal } \Rightarrow \begin{cases} \nabla f(x^*) = 0 \\ \nabla^2 f(x^*) \succcurlyeq 0 \end{cases} x∗ is Optimal ⇒{∇f(x∗)=0∇2f(x∗)≽0
证明:
- 已知 x ∗ x^* x∗是最优解,不妨设: ∇ f ( x ∗ ) ≠ 0 \nabla f(x^*) \neq 0 ∇f(x∗)=0,必然存在负梯度方向: d = − ∇ f ( x ∗ ) d = - \nabla f(x^*) d=−∇f(x∗)。
以 x ∗ x^* x∗为起始点,沿着负梯度方向前进较小的一段距离: f ( x ∗ + λ ⋅ d ) f(x^* + \lambda \cdot d) f(x∗+λ⋅d),并将其进行泰勒展开:
思路:前进一小段距离后,必然会导致目标函数值下降;从而x ∗ x^* x∗不是最优解了,产生矛盾。
f ( x ∗ + λ ⋅ d ) = f ( x ∗ ) + 1 1 ! λ [ ∇ f ( x ∗ ) ] T d + O ( λ ∥ d ∥ ) λ ∈ ( 0 , 1 ) f(x^* + \lambda \cdot d) = f(x^*) + \frac{1}{1!} \lambda [\nabla f(x^*)]^Td + \mathcal O(\lambda \|d\|) \quad \lambda \in (0,1) f(x∗+λ⋅d)=f(x∗)+1!1λ[∇f(x∗)]Td+O(λ∥d∥)λ∈(0,1)
经过整理,有:
关于λ \lambda λ范围后面不再赘述。
f ( x ∗ + λ ⋅ d ) − f ( x ∗ ) λ = [ ∇ f ( x ∗ ) ] T d + O ( λ ∥ d ∥ ) λ \frac{f(x^* + \lambda \cdot d) - f(x^*)}{\lambda} = [\nabla f(x^*)]^T d + \frac{\mathcal O(\lambda \|d\|)}{\lambda} λf(x∗+λ⋅d)−f(x∗)=[∇f(x∗)]Td+λO(λ∥d∥)
将 d = − ∇ f ( x ∗ ) d = -\nabla f(x^*) d=−∇f(x∗)代入,必然有:
[ ∇ f ( x ∗ ) ] T d = − ∣ ∣ ∇ f ( x ∗ ) ∣ ∣ 2 < 0 [\nabla f(x^*)]^T d = - ||\nabla f(x^*)||^2 < 0 [∇f(x∗)]Td=−∣∣∇f(x∗)∣∣2<0
当 λ ⇒ 0 \lambda \Rightarrow 0 λ⇒0时,有:
lim λ ⇒ 0 f ( x ∗ + λ ⋅ d ) − f ( x ∗ ) λ = lim λ ⇒ 0 { [ ∇ f ( x ∗ ) ] T d ⏟ < 0 + O ( λ ⋅ ∥ d ∥ ) λ ⏟ = 0 } < 0 \mathop{\lim}\limits_{\lambda \Rightarrow 0} \frac{f(x^* + \lambda \cdot d) - f(x^*)}{\lambda} = \mathop{\lim}\limits_{\lambda \Rightarrow 0} \left\{\underbrace{[\nabla f(x^*)]^T d}_{< 0} + \underbrace{\frac{\mathcal O(\lambda \cdot \|d\|)}{\lambda}}_{=0}\right\} < 0 λ⇒0limλf(x∗+λ⋅d)−f(x∗)=λ⇒0lim⎩ ⎨ ⎧<0 [∇f(x∗)]Td+=0 λO(λ⋅∥d∥)⎭ ⎬ ⎫<0
从而:
lim λ ⇒ 0 f ( x ∗ + λ ⋅ d ) − f ( x ∗ ) λ < 0 ⇒ lim λ ⇒ 0 f ( x ∗ + λ ⋅ d ) < f ( x ∗ ) \mathop{\lim}\limits_{\lambda \Rightarrow 0} \frac{f(x^* + \lambda \cdot d) - f(x^*)}{\lambda} < 0 \Rightarrow \mathop{\lim}\limits_{\lambda \Rightarrow 0} f(x^* + \lambda \cdot d) < f(x^*) λ⇒0limλf(x∗+λ⋅d)−f(x∗)<0⇒λ⇒0limf(x∗+λ⋅d)<f(x∗)
此时,发现了存在比 f ( x ∗ ) f(x^*) f(x∗)还要小的函数值 f ( x ∗ + λ ⋅ d ) f(x^* + \lambda \cdot d) f(x∗+λ⋅d),这意味着: x ∗ x^* x∗不是最优解。与条件矛盾,得证。也将 ∇ f ( x ∗ ) = 0 \nabla f(x^*) = 0 ∇f(x∗)=0称作一般函数 f ( ⋅ ) f(\cdot) f(⋅) x ∗ x^* x∗是最优解的一阶必要条件。 - 二阶必要条件证明:已知 x ∗ x^* x∗是最优解,必然有: ∇ f ( x ∗ ) = 0 \nabla f(x^*) = 0 ∇f(x∗)=0。假设 x ∗ x^* x∗位置的 Hessian Matrix ⇒ ∇ 2 f ( x ∗ ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(x^*) Hessian Matrix⇒∇2f(x∗)低于半正定矩阵,必然有:
∃ d ≠ 0 ⇒ d T ∇ 2 f ( x ∗ ) d < 0 \exist d \neq 0 \Rightarrow d^T \nabla^2 f(x^*) d < 0 ∃d=0⇒dT∇2f(x∗)d<0
以 x ∗ x^* x∗为起始点, d d d为下降方向前进较小的一段距离: f ( x ∗ + λ ⋅ d ) f(x^* + \lambda \cdot d) f(x∗+λ⋅d),并将其进行泰勒展开:
与平稳点的证明相似,只不过需要二阶泰勒展开~
f ( x ∗ + λ ⋅ d ) = f ( x ∗ ) + 1 1 ! λ ⋅ [ ∇ f ( x ∗ ) ] T ⏟ = 0 d + 1 2 ! λ ⋅ d T ∇ 2 f ( x ∗ ) d + O ( λ 2 ⋅ ∥ d ∥ 2 ) = f ( x ∗ ) + 1 2 ! λ ⋅ d T ∇ 2 f ( x ∗ ) d + O ( λ 2 ⋅ ∥ d ∥ 2 ) \begin{aligned} f(x^* + \lambda \cdot d) & = f(x^*) + \frac{1}{1!} \lambda \cdot \underbrace{[\nabla f(x^*)]^T}_{=0}d + \frac{1}{2!} \lambda \cdot d^T \nabla^2 f(x^*) d + \mathcal O(\lambda^2 \cdot \|d\|^2) \\ & = f(x^*) + \frac{1}{2!} \lambda \cdot d^T \nabla^2 f(x^*) d + \mathcal O(\lambda^2 \cdot \|d\|^2) \end{aligned} f(x∗+λ⋅d)=f(x∗)+1!1λ⋅=0 [∇f(x∗)]Td+2!1λ⋅dT∇2f(x∗)d+O(λ2⋅∥d∥2)=f(x∗)+2!1λ⋅dT∇2f(x∗)d+O(λ2⋅∥d∥2)
经过整理,并令 λ ⇒ 0 \lambda \Rightarrow 0 λ⇒0,有:
lim λ ⇒ 0 f ( x ∗ + λ ⋅ d ) − f ( x ∗ ) λ 2 = 1 2 d T ∇ 2 f ( x ∗ ) d ⏟ < 0 + O ( λ 2 ⋅ ∥ d ∥ 2 ) λ 2 ⏟ = 0 < 0 \mathop{\lim}\limits_{\lambda \Rightarrow 0} \frac{f(x^* + \lambda \cdot d) - f(x^*)}{\lambda^2} = \frac{1}{2}\underbrace{d^T \nabla^2 f(x^*) d}_{<0} + \underbrace{\frac{\mathcal O(\lambda^2 \cdot \|d\|^2)}{\lambda^2}}_{=0} < 0 λ⇒0limλ2f(x∗+λ⋅d)−f(x∗)=21<0 dT∇2f(x∗)d+=0 λ2O(λ2⋅∥d∥2)<0
从而 f ( x ∗ + λ ⋅ d ) < f ( x ∗ ) f(x^* + \lambda \cdot d) < f(x^*) f(x∗+λ⋅d)<f(x∗),从而与条件矛盾。因此:最优解 x ∗ x^* x∗对应的 ∇ 2 f ( x ∗ ) ≽ 0 \nabla^2 f(x^*) \succcurlyeq 0 ∇2f(x∗)≽0恒成立。
相反,如果存在某点 x ∗ x^* x∗,使得: ∇ f ( x ∗ ) = 0 \nabla f(x^*) = 0 ∇f(x∗)=0且 ∇ 2 f ( x ∗ ) ≽ 0 \nabla^2 f(x^*) \succcurlyeq 0 ∇2f(x∗)≽0,那么点 x ∗ x^* x∗是否为最优解 ? ? ?不一定。例如: f ( x ) = x 3 f(x) = x^3 f(x)=x3,其函数图像表示如下:

在 x = 0 x = 0 x=0处的梯度 ∇ f ( x ) ∣ x = 0 = 0 \nabla f(x)|_{x=0} = 0 ∇f(x)∣x=0=0;二阶梯度 ∇ 2 f ( x ) ∣ x = 0 = 0 \nabla^2 f(x) |_{x = 0} = 0 ∇2f(x)∣x=0=0,均满足条件;但该点是一个鞍点,而不是最优解点。
无约束优化问题的充分条件
如果 f ( ⋅ ) f(\cdot) f(⋅)不是凸函数,只是一般函数,如果存在某点 x ∗ x^* x∗,满足: ∇ f ( x ∗ ) = 0 , ∇ 2 f ( x ∗ ) ≻ 0 \nabla f(x^*) =0,\nabla^2 f(x^*) \succ 0 ∇f(x∗)=0,∇2f(x∗)≻0,那么 x ∗ x^* x∗是严格最优解;
其中∇ 2 f ( x ∗ ) ≻ 0 \nabla^2 f(x^*) \succ 0 ∇2f(x∗)≻0表示函数f ( ⋅ ) f(\cdot) f(⋅)在x ∗ x^* x∗点处的Hessian Matrix \text{Hessian Matrix} Hessian Matrix是正定矩阵。需要注意的是,这里的严格最优解可能是严格局部最优解或者严格全局最优解。
证明:
要证上式,即证: ∀ x ∈ N ϵ ( x ∗ ) , f ( x ∗ ) < f ( x ) \forall x \in \mathcal N_{\epsilon}(x^*),f(x^*) < f(x) ∀x∈Nϵ(x∗),f(x∗)<f(x)。
- 以 x ∗ x^* x∗为起始点,朝着任意方向 d d d前进较小的距离,得到新的函数结果: f ( x ∗ + λ ⋅ d ) f(x^* + \lambda \cdot d) f(x∗+λ⋅d)。观察: f ( x ∗ + λ ⋅ d ) f(x^* + \lambda \cdot d) f(x∗+λ⋅d)与 f ( x ∗ ) f(x^*) f(x∗)之间的大小情况。使用泰勒公式展开:
为了简单起见,仅关注d d d的方向,而令d d d大小∥ d ∥ = 1 \|d\| = 1 ∥d∥=1
f ( x ∗ + λ ⋅ d ) = f ( x ∗ ) + 1 1 ! λ ⋅ [ ∇ f ( x ∗ ) ] T ⏟ = 0 d + 1 2 ! λ 2 d T ∇ 2 f ( x ∗ ) ⏟ ≻ 0 d + O ( λ 2 ) ∥ d ∥ 2 = 1 f(x^* + \lambda \cdot d) = f(x^*) + \frac{1}{1!} \lambda \cdot\underbrace{[\nabla f(x^*)]^T}_{=0} d + \frac{1}{2!} \lambda^2 d^T \underbrace{\nabla^2 f(x^*)}_{\succ 0}d + \mathcal O(\lambda^2) \quad \|d\|^2 = 1 f(x∗+λ⋅d)=f(x∗)+1!1λ⋅=0 [∇f(x∗)]Td+2!1λ2dT≻0 ∇2f(x∗)d+O(λ2)∥d∥2=1
整理上式,观察 f ( x ∗ + λ ⋅ d ) − f ( x ∗ ) f(x^* + \lambda \cdot d) - f(x^*) f(x∗+λ⋅d)−f(x∗)结果:
lim λ ⇒ 0 f ( x ∗ + λ ⋅ d ) − f ( x ∗ ) λ 2 = 1 2 d T ∇ 2 f ( x ∗ ) d > 0 \mathop{\lim}\limits_{\lambda \Rightarrow 0} \frac{f(x^* + \lambda \cdot d) - f(x^*)}{\lambda^2} = \frac{1}{2}d^T \nabla^2 f(x^*) d > 0 λ⇒0limλ2f(x∗+λ⋅d)−f(x∗)=21dT∇2f(x∗)d>0
从而 f ( x ∗ + λ ⋅ d ) > f ( x ∗ ) f(x^* + \lambda \cdot d) > f(x^*) f(x∗+λ⋅d)>f(x∗)。这意味着:在 x ∗ x^* x∗范围的小的邻域内, f ( x ∗ ) f(x^*) f(x∗)是最小值,并且是严格最小值,得证。
Reference \text{Reference} Reference:
最优化理论与方法-第五讲-无约束优化问题(一)
相关文章:

机器学习笔记之最优化理论与方法(六)无约束优化问题——最优性条件
机器学习笔记之最优化理论与方法——无约束优化问题[最优性条件] 引言无约束优化问题无约束优化问题最优解的定义 无约束优化问题的最优性条件无约束优化问题的充要条件无约束优化问题的必要条件无约束优化问题的充分条件 引言 本节将介绍无约束优化问题,主要介绍无…...

E5061B/是德科技keysight E5061B网络分析仪
181/2461/8938产品概述 是德科技E5061B(安捷伦)网络分析仪在从5 Hz到3 GHz的宽频率范围内提供通用的高性能网络分析。E5061B提供ENA系列常见的出色RF性能,还提供全面的LF(低频)网络测量能力;包括内置1 Mohm输入的增益相位测试端口。E5061B从低频到高频的…...
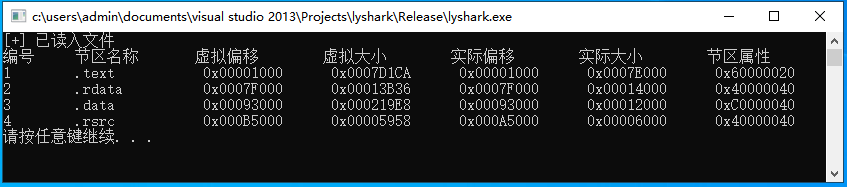
2.4 PE结构:节表详细解析
节表(Section Table)是Windows PE/COFF格式的可执行文件中一个非常重要的数据结构,它记录了各个代码段、数据段、资源段、重定向表等在文件中的位置和大小信息,是操作系统加载文件时根据节表来进行各个段的映射和初始化的重要依据…...
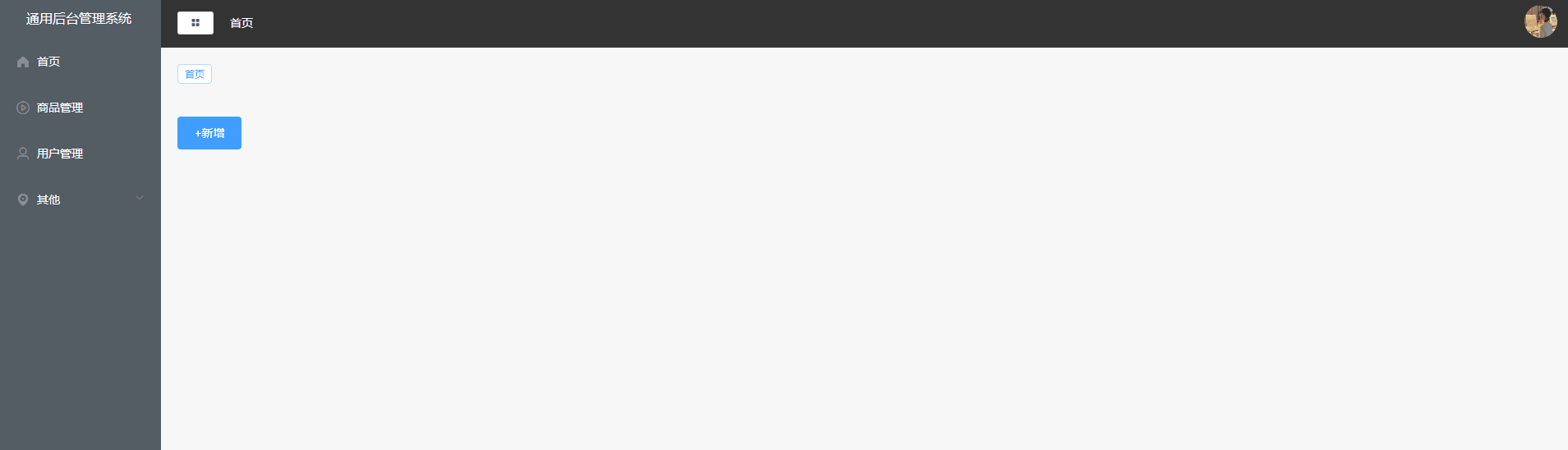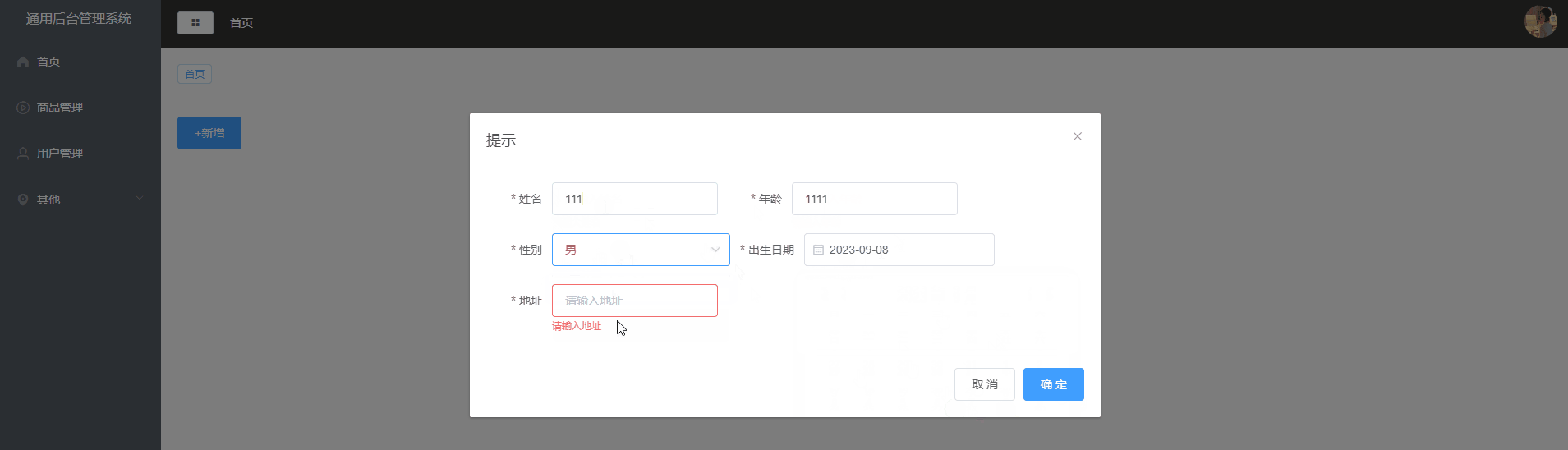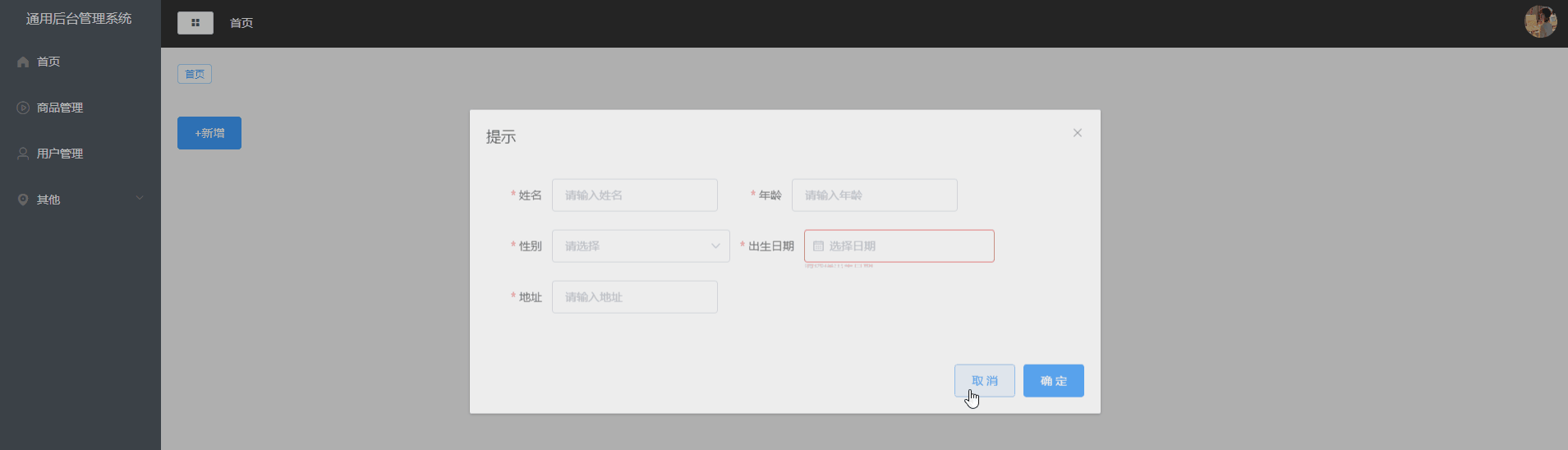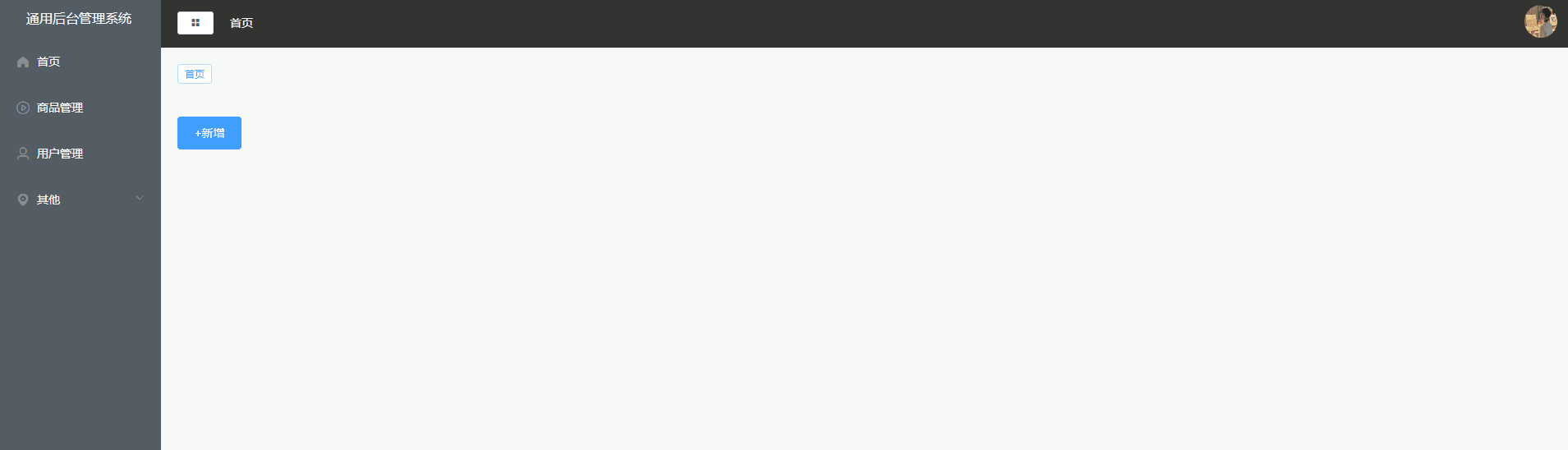
Vue2项目练手——通用后台管理项目第五节
Vue2项目练手——通用后台管理项目 首页组件布局面包屑&tag面包屑使用组件使用vuex存储面包屑数据src/store/tab.jssrc/components/CommonAside.vuesrc/components/CommonHeader.vue tag使用组件文件目录CommonTag.vueMain.vuetabs.js 用户管理页新增功能使用的组件页面布局…...

软件工程学术顶会——ESEC/FSE 2022 议题(网络安全方向)清单、摘要与总结
总结 本次会议中网络安全相关议题涵盖区块链、智能合约、符号执行、浏览器API模糊测试等不同研究领域。 热门研究方向: 1. 基于深度学习的漏洞检测与修复 2. 基于AI的自动漏洞修复 3. 模糊测试与漏洞发现 冷门研究方向: 1. 多语言代码的漏洞分析 2. 代码审查中的软件安全 3. 浏…...

从C语言到C++_36(智能指针RAII)auto_ptr+unique_ptr+shared_ptr+weak_ptr
目录 1. 智能指针的引入_内存泄漏 1.1 内存泄漏 1.2 如何避免内存泄漏 2. RAII思想 2.1 RAII解决异常安全问题 2.2 智能指针原理 3. auto_ptr 3.1 auto_ptr模拟代码 4. unique_ptr 4.1 unique_ptr模拟代码 5. shared_ptr 5.1 shared_ptr模拟代码 5.2 循环引用 6.…...
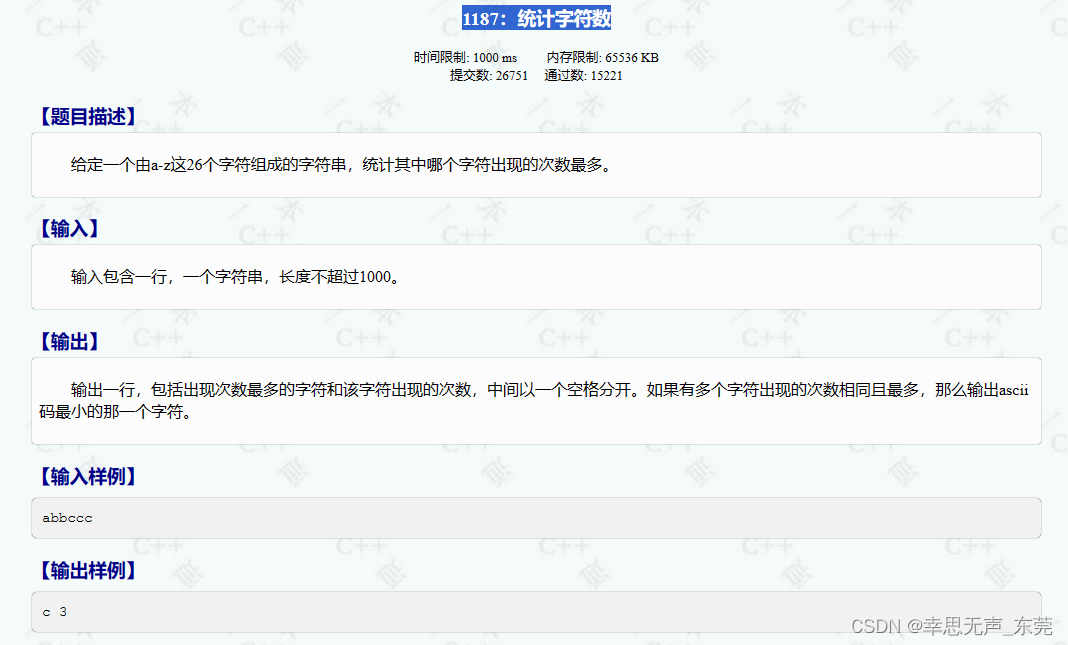
C++信息学奥赛1187:统计字符数
#include <bits/stdc.h> using namespace std; int main() {string arr;cin >> arr; // 输入一个字符串int n, a, max; // 定义变量n, a, maxchar ArrMax; // 定义字符变量ArrMaxn arr.length(); // 获取字符串长度max a 0; // 初始化max和a为0// 外层循环&…...
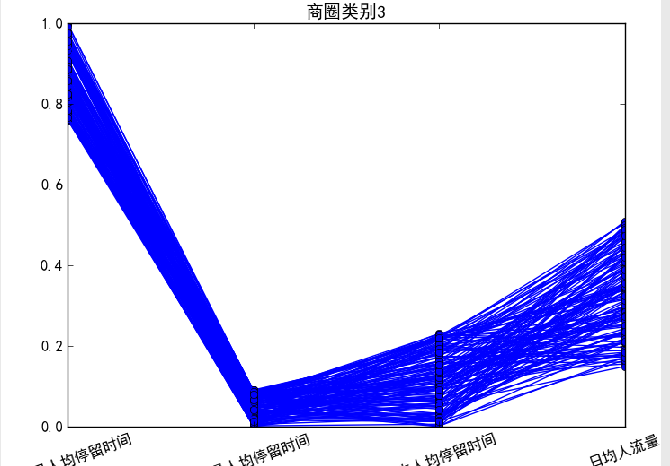
计算机毕设 大数据商城人流数据分析与可视化 - python 大数据分析
文章目录 0 前言课题背景分析方法与过程初步分析:总体流程:1.数据探索分析2.数据预处理3.构建模型 总结 最后 0 前言 🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕设题目缺少创新和亮点,往往达不到…...
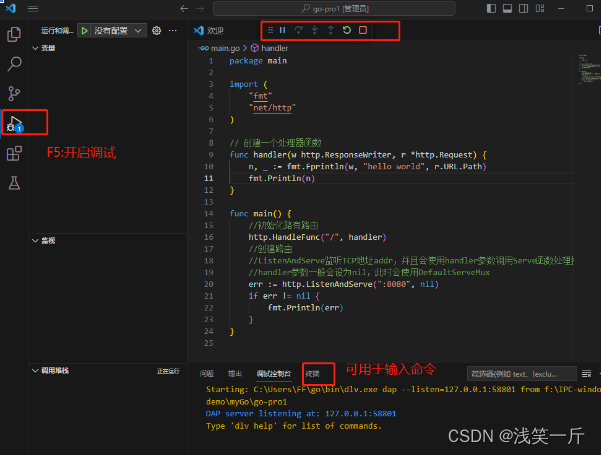
vscode上搭建go开发环境
前言 Go语言介绍: Go语言适合用于开发各种类型的应用程序,包括网络应用、分布式系统、云计算、大数据处理等。由于Go语言具有高效的并发处理能力和内置的网络库,它特别适合构建高并发、高性能的服务器端应用。以下是一些常见的Go语言应用开发…...
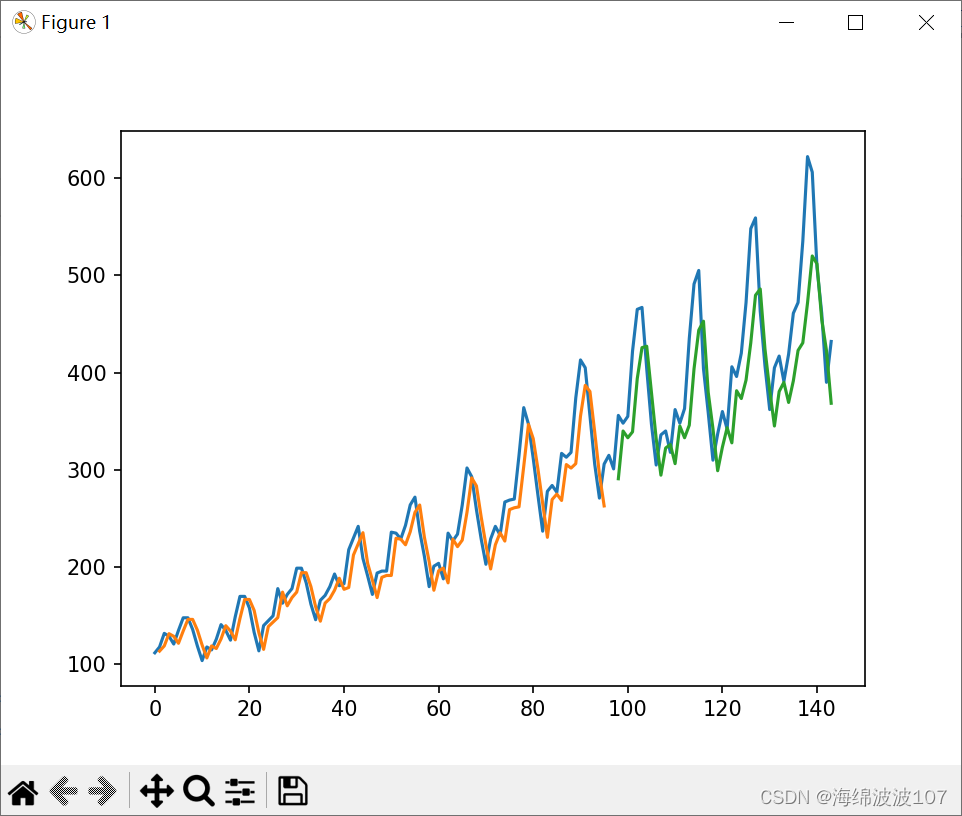
10.(Python数模)(预测模型二)LSTM回归网络(1→1)
LSTM回归网络(1→1) 长短期记忆网络 - 通常只称为“LSTM” - 是一种特殊的RNN,能够学习长期的规律。 它们是由Hochreiter&Schmidhuber(1997)首先提出的,并且在后来的工作中被许多人精炼和推广。…...

mac常见问题(五) Mac 无法开机
在mac的使用过程中难免会碰到这样或者那样的问题,本期为您带来Mac 无法开机怎么进行操作。 1、按下 Mac 上的电源按钮。每台 Mac 电脑都有一个电源按钮,通常标有电源符号 。然后检查有没有通电迹象,例如: 发声,例如由风…...

WebSocket与SSE区别
一,websocket WebSocket是HTML5下一种新的协议(websocket协议本质上是一个基于tcp的协议) 它实现了浏览器与服务器全双工通信,能更好的节省服务器资源和带宽并达到实时通讯的目的 Websocket是一个持久化的协议 websocket的原理 …...
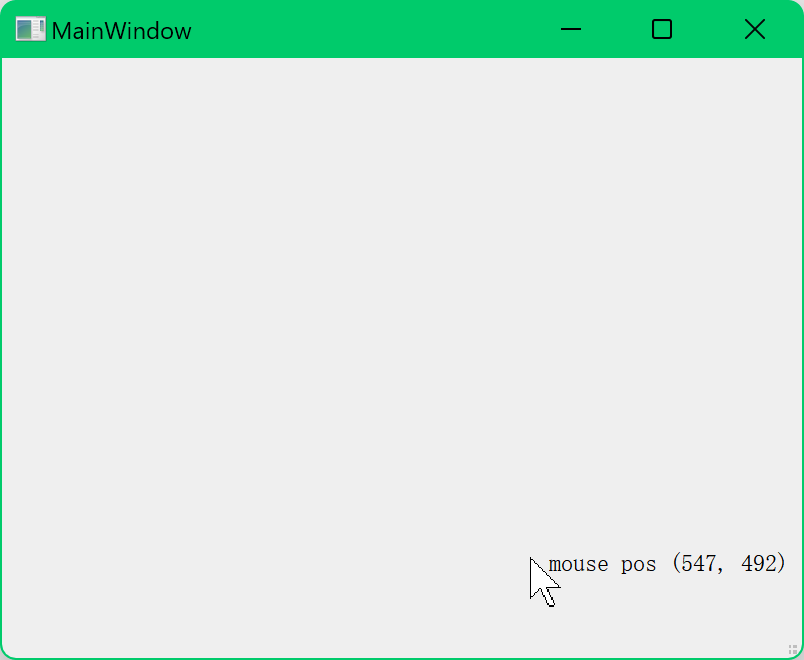
Qt鼠标点击事件处理:显示鼠标点击位置(完整示例)
Qt 入门实战教程(目录) 前驱文章: Qt Creator 创建 Qt 默认窗口程序(推荐) 什么是事件 事件是对各种应用程序需要知道的由应用程序内部或者外部产生的事情或者动作的通称。 事件(event)驱动…...

OpenCV:实现图像的负片
负片 负片是摄影中会经常接触到的一个词语,在最早的胶卷照片冲印中是指经曝光和显影加工后得到的影像。负片操作在很多图像处理软件中也叫反色,其明暗与原图像相反,其色彩则为原图像的补色。例如,颜色值A与颜色值B互为补色&#…...

HZOJ#237. 递归实现排列型枚举
题目描述 从 1−n这 n个整数排成一排并打乱次序,按字典序输出所有可能的选择方案。 输入 输入一个整数 n。(1≤n≤8) 输出 每行一组方案,每组方案中两个数之间用空格分隔。 注意每行最后一个数后没有空格。 样例…...

C++ PIMPL 编程技巧
C PIMPL 编程技巧 文章目录 C PIMPL 编程技巧什么是pimpl?pimpl优点举例实现 什么是pimpl? Pimpl (Pointer to Implementation) 是一种常见的 C 设计模式,用于隐藏类的实现细节,从而减少编译依赖和提高编译速度。它的基本思想是将…...

一个通用的EXCEL生成下载方法
Excel是一个Java开发中必须会用到的东西,之前博主也发过一篇关于使用Excel的文章,但是最近工作中,发现了一个更好的使用方法,所以,就对之前的博客进行总结,然后就有了这篇新的,万能通用的方法说…...

介绍 TensorFlow 的基本概念和使用场景。
TensorFlow(简称TF)是由Google开发的开源机器学习框架,它具有强大的数值计算和深度学习功能,广泛用于构建、训练和部署机器学习模型。以下是TensorFlow的基本概念和使用场景: 基本概念: 张量(T…...
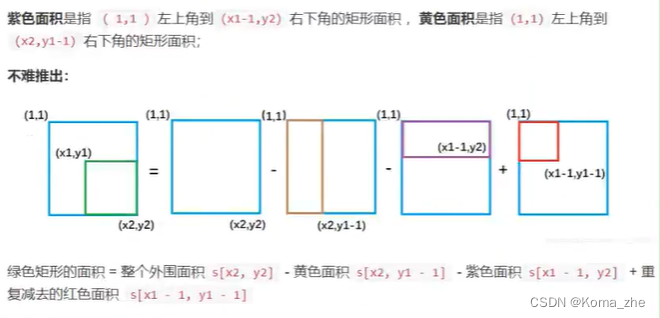
【力扣】304. 二维区域和检索 - 矩阵不可变 <二维前缀和>
目录 【力扣】304. 二维区域和检索 - 矩阵不可变二维前缀和理论初始化计算面积 题解 【力扣】304. 二维区域和检索 - 矩阵不可变 给定一个二维矩阵 matrix,以下类型的多个请求: 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, …...
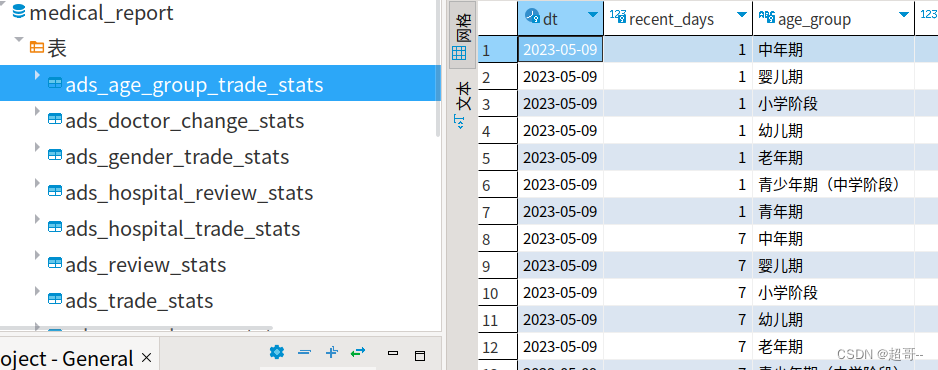
线上问诊:数仓开发(三)
系列文章目录 线上问诊:业务数据采集 线上问诊:数仓数据同步 线上问诊:数仓开发(一) 线上问诊:数仓开发(二) 线上问诊:数仓开发(三) 文章目录 系列文章目录前言一、ADS1.交易主题1.交易综合统计2.各医院交易统计3.各性…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
