计算机图形学线性代数相关概念
Transformation(2D-Model)
Scale(缩放)

[ x ′ y ′ ] = [ s 0 0 s ] [ x y ] (等比例缩放) \left[ \begin{matrix} x' \\ y' \end{matrix} \right]= \left[ \begin{matrix} s & 0 \\ 0 & s \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right] \tag{等比例缩放} [x′y′]=[s00s][xy](等比例缩放)

[ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] (x,y不同比例缩放) \left[ \begin{matrix} x' \\ y' \end{matrix} \right] =\left[ \begin{matrix} s_x & 0 \\ 0 & s_y \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right] \tag{x,y不同比例缩放} [x′y′]=[sx00sy][xy](x,y不同比例缩放)
Reflection(反转)

[ x ′ y ′ ] = [ − 1 0 0 1 ] [ x y ] (沿y轴对称反转) \left[ \begin{matrix} x' \\ y' \end{matrix} \right] =\left[ \begin{matrix} -1 & 0 \\ 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right] \tag{沿y轴对称反转} [x′y′]=[−1001][xy](沿y轴对称反转)
沿x轴或原点对称同理
Shear(切变)
如下图,切变的跨度(
a)和y是成正比例的。坐标归一化后,也就是x每次加一个y倍的a

[ x ′ y ′ ] = [ 1 a 0 1 ] [ x y ] (坐标归一化后的操作) \left[ \begin{matrix} x' \\ y' \end{matrix} \right] =\left[ \begin{matrix} 1 & a \\ 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right] \tag{坐标归一化后的操作} [x′y′]=[10a1][xy](坐标归一化后的操作)
Rotate(旋转)

R θ = [ c o s θ − s i n θ s i n θ c o s θ ] R_\theta =\left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{matrix} \right] Rθ=[cosθsinθ−sinθcosθ]
Homogenous coordinates(齐次坐标)
为什么引入齐次坐标?
区分向量和点,更易于表示仿射变换仿射变换就是线性的几何变换加上一个平移,包括旋转、缩放、平移、切变。
齐次坐标的意义就是让平移变换和其它线性变换一样,都能表述成一个矩阵相乘的形式!
具体做法:
Add a third coordinate (w-coordinate)
- 2D point = ( x , y , 1 ) T (x,y,1)^T (x,y,1)T
- 2D vector = ( x , y , 0 ) T (x,y,0)^T (x,y,0)T
向量具有平移不变性,只表示方向和大小!
运算过程中 w 分量的值:
- vector + vector = vector 向量+向量结果依旧为向量,w此时仍为0
- point - point = vector 点-点结果为向量,w此时为0
- point + vector = point 点+向量结果为点,w此时为1
- point + point = ?? 点+点 无意义? ,w此时为2
- 扩充意义:点 + 点 = 两个点的中点
w ! = 0 , [ x y w ] = [ x / w y / w w / w ] = [ x / w y / w 1 ] w != 0, \left[ \begin{matrix} x \\ y \\ w \end{matrix} \right] = \left[ \begin{matrix} x/w \\ y/w \\ w/w \end{matrix} \right] =\left[ \begin{matrix} x/w \\ y/w \\ 1 \end{matrix} \right] w!=0, xyw = x/wy/ww/w = x/wy/w1
Translation(平移)
translation is NOT linear transform!
平移不是线性变换,线性变换的对象是向量,向量是不存在空间位置的!平移是对点进行操作。

[ x ′ y ′ w ′ ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y w ] = [ x + t x y + t y w ] (向量的w为0,点的w为1) \left[ \begin{matrix} x' \\ y' \\ w' \end{matrix} \right] =\left[ \begin{matrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ w \end{matrix} \right] = \left[ \begin{matrix} x + t_x \\ y + t_y \\ w \end{matrix} \right] \tag{向量的w为0,点的w为1} x′y′w′ = 100010txty1 xyw = x+txy+tyw (向量的w为0,点的w为1)
引入齐次坐标后的变换矩阵
Scale
S ( s x , s y ) = [ s x 0 0 0 s y 0 0 0 1 ] S(s_x, s_y) =\left[ \begin{matrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{matrix} \right] S(sx,sy)= sx000sy0001
Rotation
R θ = [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] R_\theta =\left[ \begin{matrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] Rθ= cosθsinθ0−sinθcosθ0001
Translation
T ( t x , t y ) = [ 1 0 t x 0 1 t y 0 0 1 ] T(t_x, t_y)= \left[ \begin{matrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{matrix} \right] T(tx,ty)= 100010txty1
Other
逆变换
执行一个操作,再执行这个操作的逆操作,相当于不变。

变换顺序
根据矩阵的分配率性质,多个操作可以合并成一个矩阵。

变换组合到一个矩阵时,先进行线性变换,再进行平移。
[ x ′ y ′ 1 ] = [ a b t x c d t y 0 0 1 ] [ x y 1 ] \left[ \begin{matrix} x' \\ y' \\ 1 \end{matrix} \right] = \left[ \begin{matrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] x′y′1 = ac0bd0txty1 xy1
变换的分解
Q:如何围绕给定点进行旋转(非原点)?
A:1.平移到原点 2.旋转 3.反向平移复位

Transformation(3D-Model)
Use homogeneous coordinates again:
- 3D point = ( x , y , z , 1 ) T (x,y,z,1)^T (x,y,z,1)T
- 3D vector = ( x , y , z , 0 ) T (x,y,z,0)^T (x,y,z,0)T
w 分量不为0时的扩充意义:
w ! = 0 , [ x y z w ] = [ x / w y / w z / w w / w ] = [ x / w y / w z / w 1 ] w != 0, \left[ \begin{matrix} x \\ y \\ z \\ w \end{matrix} \right]=\left[ \begin{matrix} x/w \\ y/w \\ z/w \\ w/w \end{matrix} \right] =\left[ \begin{matrix} x/w \\ y/w \\ z/w \\ 1 \end{matrix} \right] w!=0, xyzw = x/wy/wz/ww/w = x/wy/wz/w1
Use 4x4 matrices for affine(仿射) transformations
[ x ′ y ′ z ′ 1 ] = [ a b c t x d e f t y g h i t z 0 0 0 1 ] [ x y z 1 ] \left[ \begin{matrix} x' \\ y' \\ z' \\ 1 \end{matrix} \right] =\left[ \begin{matrix} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ z \\ 1 \end{matrix} \right] x′y′z′1 = adg0beh0cfi0txtytz1 xyz1
先进行线性变换,再进行平移。
Rotation around x,y or z-axis沿着标准轴旋转

R x ( α ) = [ 1 0 0 0 0 c o s α − s i n α 0 0 s i n α c o s α 0 0 0 0 1 ] − − − − − − − − − − − − − − − − − − − − − − − − − R y ( α ) = [ c o s α 0 s i n α 0 0 1 0 0 − s i n α 0 c o s α 0 0 0 0 1 ] − − − − − − − − − − − − − − − − − − − − − − − − − R z ( α ) = [ c o s α − s i n α 0 0 s i n α c o s α 0 0 0 0 1 0 0 0 0 1 ] R_x(\alpha) =\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha & 0 \\ 0 & sin\alpha & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \\ \\ ------------------------- \\ R_y(\alpha) =\left[ \begin{matrix} cos\alpha & 0 & sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -sin\alpha & 0 & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \\ \\ ------------------------- \\ R_z(\alpha) =\left[ \begin{matrix} cos\alpha & -sin\alpha & 0 & 0 \\ sin\alpha & cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] Rx(α)= 10000cosαsinα00−sinαcosα00001 −−−−−−−−−−−−−−−−−−−−−−−−−Ry(α)= cosα0−sinα00100sinα0cosα00001 −−−−−−−−−−−−−−−−−−−−−−−−−Rz(α)= cosαsinα00−sinαcosα0000100001
Compose any 3D rotation from Rx,Ry, Rz沿着任意轴旋转

如图,α β γ分别对应roll pitch yaw(欧拉角)。
- Roll:翻滚,我们以圣地安列斯里最恶心的开飞机为例,Roll将你的飞机机头朝向不变,进行机身的转动,机翼从水平到竖直这种。
- Pitch:是将你的飞机机头向上抬或者向下降,范围在-90 ~ 90 .
- Yaw:是水平方向上转动机头的朝向,范围在0~360。
图形学中有一个办法,可以把任意的一个旋转分解再X,Y,Z三轴上,分别做旋转从而得到了一个公式,也就是罗德里德斯旋转公式:

罗德里德斯旋转公式给了我们一个旋转矩阵,它定义了一个旋转轴 n 和一个旋转角度 α。
我们默认旋转轴 n 是过原点的,也就是起点在原点上,方向是n这个方向,旋转角度为α。
如果想要沿着任意轴旋转,但该轴起点不是原点,则需要先将所有的物体都进行平移是的旋转轴的起点为原点,然后进行旋转,最后再平移回去。
矩阵N是两个向量叉乘写成矩阵形式。
Transformation(View/Camera)
前置概念Ⅰ:旋转矩阵的逆矩阵等于它的转置矩阵
R θ = [ c o s θ − s i n θ s i n θ c o s θ ] − − − − − − − − − − − − − R − θ = [ c o s θ s i n θ − s i n θ c o s θ ] ★ R − θ = R θ − 1 = R θ T R_\theta = \left[ \begin{matrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \\ \end{matrix} \right] \\ \\ ------------- \\ R_{-\theta} = \left[ \begin{matrix} cos\theta & sin\theta\\ -sin\theta & cos\theta \\ \end{matrix} \right] \\ \\ ★ R_{-\theta}=R_{\theta}^{-1}=R_{\theta}^T Rθ=[cosθsinθ−sinθcosθ]−−−−−−−−−−−−−R−θ=[cosθ−sinθsinθcosθ]★R−θ=Rθ−1=RθT
如上公式,从矩阵中我们可以发现 R − θ = R θ T R_{-\theta}=R_{\theta}^T R−θ=RθT而在图形学中我们知道 R θ R_{\theta} Rθ 和 R − θ R_{-\theta} R−θ 是一个互逆的操作
因此 R − θ = R θ − 1 = R θ T R_{-\theta}=R_{\theta}^{-1}=R_{\theta}^T R−θ=Rθ−1=RθT
因此我们可以得出 旋转矩阵的逆等于它的转置矩阵 这一定义,之后的内容我们会用到这个性质。
在数学上,一个矩阵的逆等于它的转置矩阵我们称其为正交矩阵。
前置概念Ⅱ:变换过程
我们知道我们需要将三维空间中摄像机看到的场景最终变为一张2D的图片给显示在screen上,我们来了解具体发生了什么变换。具体是去了解如何从3D 变为 2D。
其中的过程类似于拍照片:
- Model Transformation: 让人们集合在一起并摆好姿势(设置好场景)
- View Transformation : 找到一个拍摄的角度(设置好camera位置和看的方向)
- Projection Transformation: 拍照(将camera看向的3D内容变为2D照片)
我们主要对第二步进行讲解。
首先需要定义好Camera:
- 设置好相机的位置 Position
- 设置好相机看向的方向,即 look-at / gaze direction
- 我们除了相机指向的方向我们还要设置一个 up-direction,因为我们需要从不同角度看向场景,就像你拿着手机倾斜45度或者反着拍,最后的照片是不一样的。

至此我们通过一个点(向量),两个(单位)向量将相机给固定下来了
我们知道,当相机和物体进行相对运动时,不论怎么移动二者,我们看到的结果是一样的。

因此我们将相机从原本位置移动到原点位置,使得其Look-at direction看向 -z 方向,up-direction 是 y 正半轴。相机移动后,物体/场景跟着相机进行相同的移动,这样虽然进行了移动,但最终看到的结果是相同的。
这样做是因为可以简化很多操作,相机在(0,0,0)位置有很多的好处。

假设我们现在有一个相机,在 e 点上,gaze direction 是向量 g,up direction 是 t,我们要把点 e 给变成原点,向量 g 在 -z 轴上,t 在 y 正半轴上。
其基本思想是:
-
进行平移,将
e点移到原点。 -
旋转
g到-z方向上。 -
旋转
t到+y方向上。 -
旋转
g叉乘t得到的向量 到+x方向上。

由于我们说过一般是先进行线性变换再进行平移的,但在这里是先平移再线性变换,所以我们将T写在最右边。
平移矩阵很好写,难的是如何将g,t,g×t旋转到x,y,-z上。这时可以反过来想,我们知道g,t,g×t是如何用(x,y,z)表示的,我们只需要求出x,y,-z旋转到g,t,g×t的旋转矩阵,再加上旋转矩阵的逆矩阵 是这个旋转矩阵的转置矩阵这条性质,就可以巧妙的求出g,t,g×t给旋转到x,y,-z上的旋转矩阵。
View Transform主要做两步:
- 移动camera,使其位于world space的坐标原点,同样的将其余场景也进行相同的变换使其到应到的位置。
- 旋转camera,使得摄像机坐标系与世界坐标系重合。
Transformation(Projection)
Orthographic projection (正交投影) :多用于工程制图
Perspective projection(透视投影):符合人眼的成像,会产生近大远小的效果,看起来平行线不会平行,延长的话会相交。

正交投影和透视投影本质的区别就是:是否有近大远小的效果

Orthographic projection

正交投影的思想:
Ⅰ. 我们设置camera于原点,看向-Z方向,向上是Y轴
Ⅱ. 然后我们舍弃Z轴也就是让所有物体都Z都等于0,从而我们实现了所有物体只在X轴和Y轴上
Ⅲ. 将其挤压到 [ − 1 , 1 ] ∗ [ − 1 , 1 ] [-1, 1] * [-1, 1] [−1,1]∗[−1,1]这么一个正方形内.

图形学中的实际操作:
我们定义一个立方体,left,right bottom,top far,near(但是注意我们是看向-Z方向的,far的Z轴值小,near的值大)
然后将其的中心平移到原点出,最后将其给拉成一个 [ − 1 , 1 ] 3 [-1, 1]^3 [−1,1]3的正则立方体。
具体的操作矩阵:
M o r t h o = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] M_{ortho} =\left[ \begin{matrix} {2 \over {r-l}} & 0 & 0 & 0 \\ 0 & {2 \over {t-b}} & 0 & 0 \\ 0 & 0 & {2 \over {n-f}} & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 & -{{r+l} \over 2} \\ 0 & 1 & 0 & -{{t+b} \over 2} \\ 0 & 0 & 1 & -{{n+f} \over 2} \\ 0 & 0 & 0 & 1 \end{matrix} \right] Mortho= r−l20000t−b20000n−f200001 100001000010−2r+l−2t+b−2n+f1
具体来说第一个右侧矩阵是反向平移操作,将立方体的中心点平移到原点,类似二分找中点。第二个左侧矩阵是缩放到 [ − 1 , 1 ] 3 [-1, 1]^3 [−1,1]3内,因为边长是2,所以分子设置为2,相当于等比例交叉相乘。
Perspective projection

透视投影的思想:
Ⅰ. 将frustum给挤压成一个长方体,也就是将远平面压的和近平面一个大小。
Ⅱ. 做一次正交投影,将长方体的中心移到原点并将其压缩成 [ − 1 , 1 ] 3 [-1, 1]^3 [−1,1]3的正方体。
注意:
Ⅰ. 在挤压的过程中,近平面永远不会发生变化。
Ⅱ. 在挤压过程中,远平面上的Z值不会发生变化。
Ⅲ. 挤压过程中,远平面的中心点也不会发生变化。
关于Z值会发生改变的情况,可以想象一个场景。在你的面前是一条笔直的上山铁轨,随着距离越远,枕木之间的压缩距离应该越近。
我们知道如何做正交投影,那么接下来来讨论挤压这个frustum的矩阵如何求?


首先上图鼠标所在的右侧虚线并不是特指远平面,而是近平面到远平面之间的任意面(包含远平面)。
那么此时图中出现一组相似三角形,根据边的比例关系和已知的近平面Z值以及待挤压点的信息,可以得到挤压后点的 x ′ , y ′ x',y' x′,y′
在齐次坐标中的表示形式:
[ x y z 1 ] → [ n x / z n y / z u n k n o w n 1 ] = = [ n x n y s t i l l u n k n o w n z ] \left[ \begin{matrix} x \\ y \\ z \\1\end{matrix} \right] →\left[ \begin{matrix} nx/z \\ ny/z \\ unknown \\1 \end{matrix} \right] ==\left[ \begin{matrix} nx \\ ny \\ still \ \ \ unknown \\ z \end{matrix} \right] xyz1 → nx/zny/zunknown1 == nxnystill unknownz
挤压矩阵:
M p e r s p → o r t h o [ x y z 1 ] = [ n x n y u n k n o w n z ] M_{persp→ortho} \left[ \begin{matrix} x \\ y \\ z \\ 1 \end{matrix} \right] =\left[ \begin{matrix} nx \\ ny \\ unknown \\ z \end{matrix} \right] Mpersp→ortho xyz1 = nxnyunknownz
M p e r s p → o r t h o = [ n 0 0 0 0 n 0 0 ? ? ? ? 0 0 1 0 ] M_{persp→ortho}= \left[ \begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{matrix} \right] Mpersp→ortho= n0?00n?000?100?0
从而我们求出了除第三行以外的内容,接下来我们求第三行,但我们需要记住两点:
- 近平面上的任意一点都不会因变换而改变。


x、y依旧是变量,而替换之后的n为常量代表的是近平面的距离。总的来说就是用上述性质得到了一组
unknown为 n 2 n^2 n2的特例。
- 远平面上的任意一点的Z值都不会因变化而改变,并且中心点的X,Y也不会发生改变。

同样的,由于远平面任意一点的Z值不发生改变,取远平面的中心点(其被挤压后X和Y仍为0,且Z值不变),其坐标为(0,0,f,1)
最终推导出A,B的值,从而得到挤压矩阵 M p e r s p → o r t h o M_{persp→ortho} Mpersp→ortho。

M p e r s p → o r t h o = [ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] M_{persp→ortho}= \left[ \begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{matrix} \right] Mpersp→ortho= n0000n0000n+f100−nf0
投影透视结论: M p e r s p = M o r t h o M p e r s p → o r t h o M_{persp}=M_{ortho}M_{persp→ortho} Mpersp=MorthoMpersp→ortho
相关文章:

计算机图形学线性代数相关概念
Transformation(2D-Model) Scale(缩放) [ x ′ y ′ ] [ s 0 0 s ] [ x y ] (等比例缩放) \left[ \begin{matrix} x \\ y \end{matrix} \right] \left[ \begin{matrix} s & 0 \\ 0 & s \end{matrix} \right] \left[ \begin{matrix} x \\ y \en…...

开源PHP 代挂机源码,可对接QQ、网易云、哔哩哔哩、QQ空间、等级加速等等
本程序运行环境PHP5.6 95dg/config.php修改系统数据库 进入数据库绑定 你搭建的域名即可 部署完成 进入数据库 找到data 输入绑定授权域名即可进行授权打开此网站 网站是无对接接口 需要您自行找对接接口即可 本源码有点乱 有实力的铁铁 可以修改一下哦!...

【仿牛客论坛java项目】第五章 Kafka,构建TB级异步消息系统:阻塞队列、Kafka入门、Spring整合Kafka、发送系统通知、显示系统通知
这里写自定义目录标题 一、阻塞队列简单的阻塞队列测试案例总结阻塞队列 二、Kafka入门1、基础知识Kafka术语消息队列实现方式两种 2、配置3、启动全部命令启动 zookeeper 服务器再启动 kafka 服务器创建Topic关闭 4、总结Kafka的特点Kafka的术语 三、 Spring整合Kafka导入依赖…...
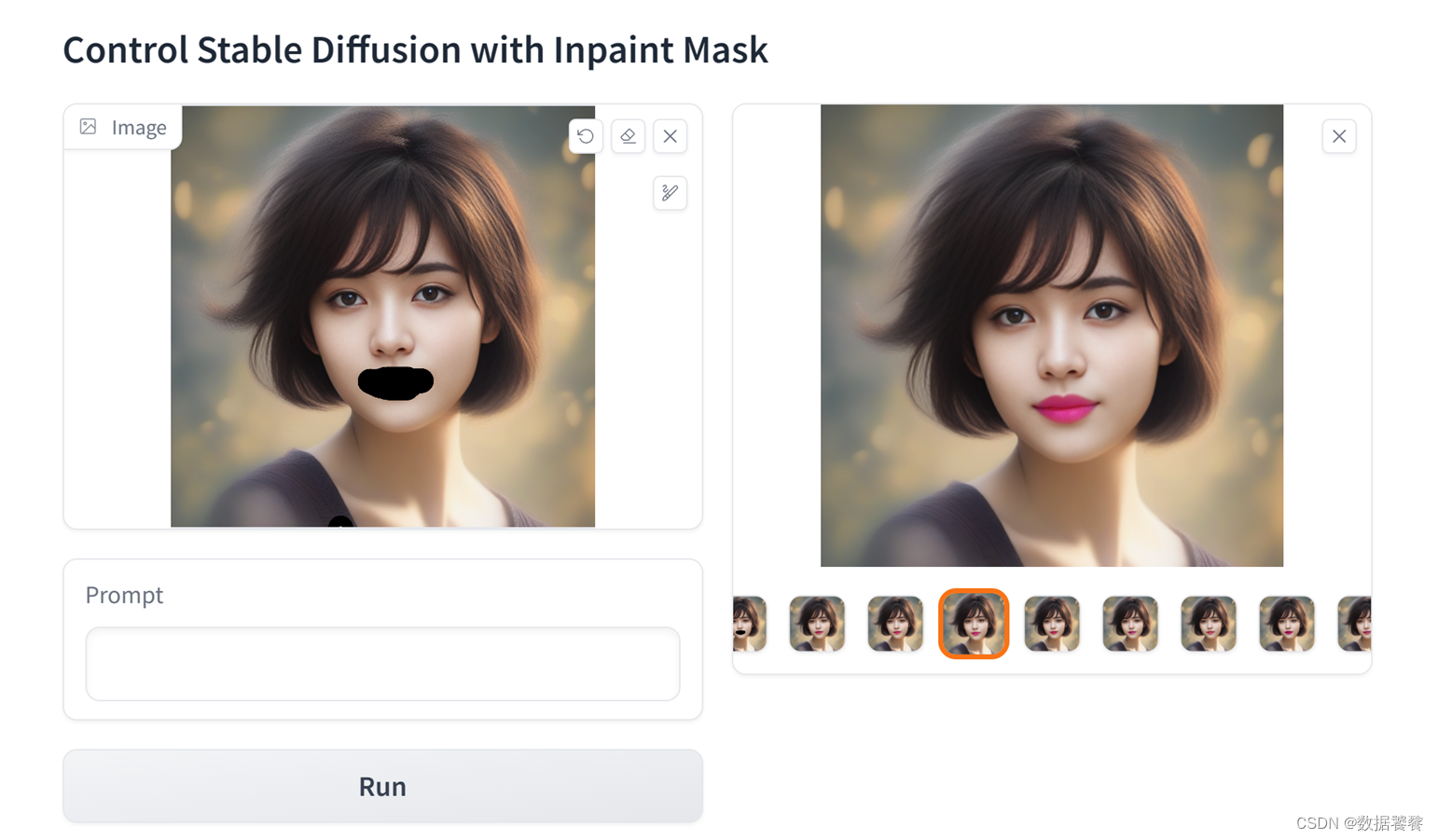
【AIGC专题】Stable Diffusion 从入门到企业级实战0401
一、概述 本章是《Stable Diffusion 从入门到企业级实战》系列的第四部分能力进阶篇《Stable Diffusion ControlNet v1.1 图像精准控制》第01节, 利用Stable Diffusion ControlNet Inpaint模型精准控制图像生成。本部分内容,位于整个Stable Diffusion生…...
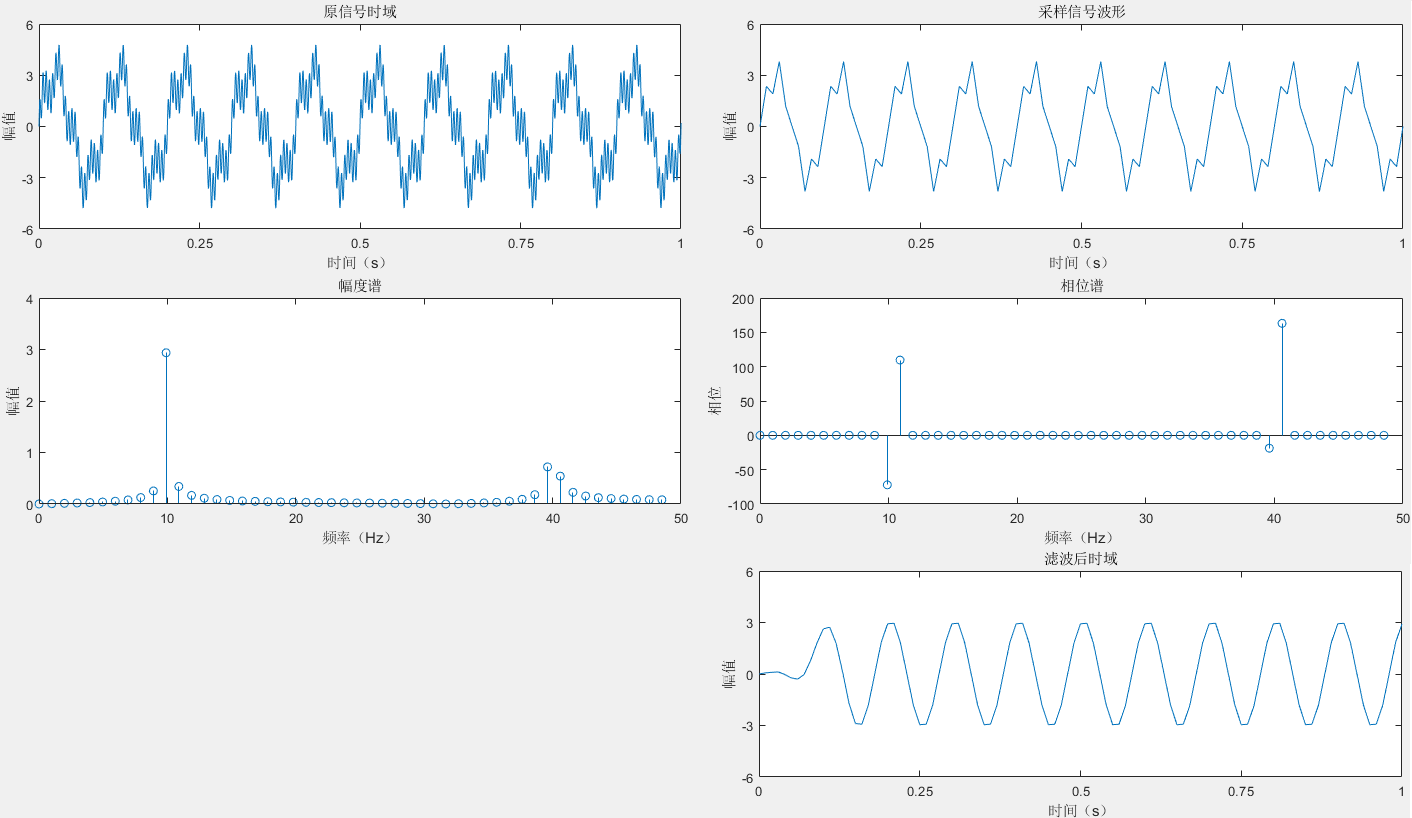
Matlab信号处理1:模拟去除信号噪声
由于工作内容涉及信号系统、信号处理相关知识,本人本硕均为计算机相关专业,专业、研究方向均未涉及信号相关知识,因此需进行系统地学习。之前已将《信号与系统》快速过了一遍,但感觉较抽象且理解较浅显。在此系统地学习如何使用Ma…...

Bootstrap的行、列布局设计(网络系统设计)
目录 00-基础知识01-等宽列布局02-指定某一列的宽度03-根据内容自动改变列的宽度04-五种预定义列宽度 .col、.col-sm-*、.col-md-*、.col-lg-*、.col-xl-*05-不同视口宽度按不同的分列方案划分06-删除列内容的盒模型的外边距07-超过12列怎么办?08-重新排列各列的顺序…...

1.1 计算机网络在信息时代中的作用
思维导图: 正文: 我的理解: 这段话是一本书或课程的第一章简介,它的目的是为读者或学生提供一个关于计算机网络基础知识的框架或大纲。 首先,它强调了这章是整本书的一个概览,会先介绍计算机网络在信息时…...

mysql CONCAT使用
问题 有一个查找数据的mysql语句:SELECT DISTINCT fund_id,version,statistic_date FROM fund_nv_divident WHERE version ( SELECT max(version) FROM fund_nv_divident) and statistic_date > ‘2023-06-04’ and fund_id not in (SELECT DISTINCT fund_id f…...

maven基础学习
什么是maven 构建 依赖 maven核心概念坐标 在黑窗口使用maven命令生成maven工程 pom.xml 想导入哪个jar包把它的坐标放到dependency里就可以 maven核心概念POM maven核心概念约定的目录结构 执行maven的构建命令 清理操作,clean 编译操作 compile 测试操作 test 打包…...

uniapp移动端地图,点击气泡弹窗并实现精准定位
记录移动端地图map组件的使用 需求记录: 移动端地图部分需要展示两个定位点,上报点及人员定位点。通过右上角的两个按钮实现地图定位。点击对应定位气泡,弹出定位点的信息。 效果图如下: map在nvue中的使用。直接用nvue可以直接…...

2023牛客暑期多校训练营7 CI「位运算」「根号分治+容斥」
C-Beautiful Sequence_2023牛客暑期多校训练营7 (nowcoder.com) 题意: 给定一个b序列,a序列满足 a [ i − 1 ] < a [ i ] a[i-1]<a[i] a[i−1]<a[i]且 a [ i ] ⊕ a [ i 1 ] b [ i ] a[i]\oplus a[i1]b[i] a[i]⊕a[i1]b[i],求字…...

YOLOv5算法改进(10)— 替换主干网络之GhostNet
前言:Hello大家好,我是小哥谈。GhostNet是一种针对计算机视觉任务的深度神经网络架构,它于2020年由中国科学院大学的研究人员提出。GhostNet的设计目标是在保持高精度的同时,减少模型的计算和存储成本。GhostNet通过引入Ghost模块…...

Android Canvas的使用
android.graphics.Canvas 一般在自定义View中,重写 onDraw(Canvas canvas) 方法时用到。 /*** Implement this to do your drawing.** param canvas the canvas on which the background will be drawn*/Overrideprotected void onDraw(Canvas canvas) {super.onDra…...
)
AI批量写文章伪原创:基于ChatGPT长文本模型,实现批量改写文章、批量回答问题(长期更新)
import traceback import openai import osopenai.api_key = ""conversation=[{"role": "system", "content": "You are a helpful assistant."}] max_history_len = 20 first_message = Nonedir = rJ:\ai\input #要改写的文…...

git常用场景记录 | 拉取远程分支A合并到本地分支B - 删除上一次的commit
文章目录 git常用场景记录拉取远程分支A合并到本地分支B本地分支B存在未add与commit的代码 删除上一次的commit已经push到远程库 git常用场景记录 doing,最后更新9.5 拉取远程分支A合并到本地分支B 需求描述 在团队合作时,我自己的本地分支B功能已经实现…...
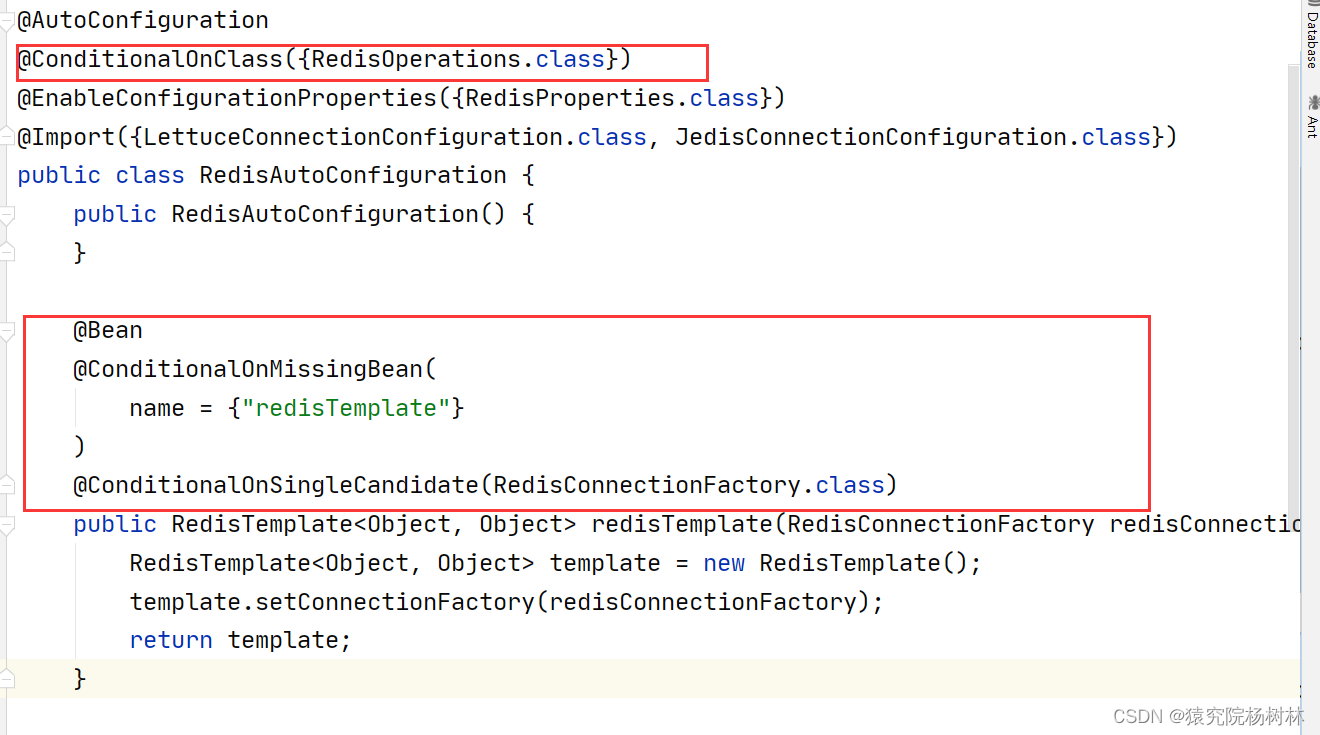
源码角度解析SpringBoot 自动配置
文章目录 前言一、了解相关注解1.Condition注解2.Enable注解 二、SpringBoot自动配置1.SpringBootApplication注解2.SpringBootConfiguration注解3.EnableAutoConfiguration注解4.Conditional注解 总结 前言 Spring Boot 自动配置是 Spring Boot 的核心特性之一,它…...

【原创】H3C路由器OSPF测试
网络拓扑图 路由器配置: 路由器1上接了4跟线,分别为这四个接口配置IP地址。 # interface GigabitEthernet0/0/0port link-mode routecombo enable copperip address 2.1.1.2 255.255.255.0 # interface GigabitEthernet0/0/1port link-mode routecombo…...

计算机视觉:轨迹预测综述
计算机视觉:轨迹预测综述 轨迹预测的定义轨迹预测的分类基于物理的方法(Physics-based)基于机器学习的方法(Classic Machine Learning-based)基于深度学习的方法(Deep Learning-based)基于强化学…...

三维跨孔电磁波CT数据可视化框架搭建
三维跨孔电磁波CT数据可视化框架搭建 文章目录 三维跨孔电磁波CT数据可视化框架搭建1、三维CT可视化结果2、matlab代码2.1、CT数据格式整理并保存2.2、三维可视化 利用matlab实现对跨孔电磁波CT实测数据反演,并搭建了三维CT数据可视化框架,可装填实测CT反…...

OC和Swift混编,导入头文件‘xxx-Swift.h‘ file not found
在OC的项目里加入Swift代码,创建完桥接文件后,需要倒入Swift头文件,头文件的格式为“项目名-Swift.h”。 如下图,我在Xcode上看到我的项目名为YichangPark,导入 #import "YiChangPark-Swift.h" 之后提示 “Y…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
