强化学习算法总结 2
强化学习算法总结 2
4.动态规划
待解决问题分解成若干个子问题,先求解子问题,然后得到目标问题的解
需要知道整个状态转移函数和价值函数,状态空间离散且有限
- 策略迭代:
- 策略评估:贝尔曼期望方程来得到一个策略的 V ( s ) V(s) V(s)
- 策略提升:
- 价值迭代
4.1 策略迭代算法
- 策略评估
V ( S ) = ∑ a π ( a ∣ s ) Q ( s , a ) = ∑ a π ( a ∣ s ) ( r ( a , s ) + γ ∑ s P ( s ′ ∣ s , a ) V π ( S ′ ) ) V(S) = \sum_a \pi(a|s)Q(s,a) = \sum_a \pi(a|s)(r(a,s)+ \gamma\sum_s P(s'|s,a)V^\pi(S')) V(S)=a∑π(a∣s)Q(s,a)=a∑π(a∣s)(r(a,s)+γs∑P(s′∣s,a)Vπ(S′))
知道状态转移函数和未来状态价值就可以估计当前的状态:我们只需要求解 V ( s ) V(s) V(s)
这里就是利用贝尔曼方程,来不断地更新 V ( s ) V(s) V(s),
V ( S ) k + 1 = ∑ a π ( a ∣ s ) Q ( s , a ) = ∑ a π ( a ∣ s ) ( r ( a , s ) + γ ∑ s P ( s ′ ∣ s , a ) V k ( S ′ ) ) V(S)^{k+1} = \sum_a \pi(a|s)Q(s,a) = \sum_a \pi(a|s)(r(a,s)+ \gamma\sum_s P(s'|s,a)V^k(S')) V(S)k+1=a∑π(a∣s)Q(s,a)=a∑π(a∣s)(r(a,s)+γs∑P(s′∣s,a)Vk(S′))
-
策略提升
只要当前状态下的策略的得到的状态动作函数比 V ( S ) V(S) V(S)高一些
π ′ ( s ) = a r g m a x a Q π ( s , a ) \pi'(s) = argmax_aQ^\pi(s,a) π′(s)=argmaxaQπ(s,a) -
策略迭代
π 0 策略评估 V π 0 ( S )策略提升 π 1 \pi^0 策略评估 V\pi_0(S)策略提升 \pi^1 π0策略评估Vπ0(S)策略提升π1
- 代码
- 策略评估
w h i l e max > θ d o : m a x = 0 f o r s i n r a n g e ( S ) : v = V ( s ) (所有 Q ( s , a )求和 ) V ( S ) = ( b e l l m a n f u c t i o n ) m a x = m a x ( m a x , V ( s ) − v ) while \ \max \ >\theta \ do: \\ \ max = 0 \\ \ for \ s \ in \ range(S):\\ \ v = V(s)(所有Q(s,a)求和)\\ \ V(S) = (bellman fuction)\\ \ max = max(max,V(s) - v) while max >θ do: max=0 for s in range(S): v=V(s)(所有Q(s,a)求和) V(S)=(bellmanfuction) max=max(max,V(s)−v)
* 策略提升
f o r s i n S : π ( s ) = a r g m a x ( Q ( s , a ) ) for\ s\ in\ S:\\ \pi (s) = argmax(Q(s,a)) for s in S:π(s)=argmax(Q(s,a))
4.2 价值迭代算法
V k + 1 ( s ) = m a x a { r ( s , a ) + γ ∑ s P V k } V^{k+1}(s) = max_a\{ r(s,a)+\gamma\sum_sPV^k\} Vk+1(s)=maxa{r(s,a)+γs∑PVk}
可以理解为只执行一轮的策略迭代算法
5 时序差分算法
在数据分布未知的情况下来对模型进行更新,通过智能体与环境的交互进行学习。无模型的强化学习。
- 在线强化学习:使用当前策略下采样得到的数据进行学习
- 离线强化学习:使用经验回访池
5.1 时序差分
V ( S t ) = V ( s t ) + α [ G t − V ( s t ) ] V(S_t) = V(s_t) +\alpha[G_t - V(s_t)] V(St)=V(st)+α[Gt−V(st)]
G t G_t Gt表示整个序列采集结束之后,得到的回报。而很多时候我们是没有办法
V ( s t ) + = α [ r t + γ V ( s t + 1 ) − V ( s t ) ] V(s_t) += \alpha[r_t + \gamma V(s_{t+1}) -V(s_t) ] V(st)+=α[rt+γV(st+1)−V(st)]
用时序差分法估计到了状态价值函数 V ( s ) V(s) V(s)
5.2 SARSA
Q ( s , a ) + = α [ r ( s , a ) + γ Q ( s , a ) − Q ( s , a ) ] Q(s,a) += \alpha[r(s,a) + \gamma Q(s,a) - Q(s,a)] Q(s,a)+=α[r(s,a)+γQ(s,a)−Q(s,a)]
$$
\begin{equation}
\pi(a|s)=\left{
\begin{aligned}
argmax(Q(s,a))& \ & if \ prob < \ 1- \epsilon \
random & \ & \
\end{aligned}
\right.
\end{equation}
$$
5.3 多步Sarsa
MC方法是无偏估计但是方差比较大
TD 是有偏估计,因为每一个对下一个状态的价值都是估计的
Q ( s t , a t ) + = α [ r t + γ Q ( s t + 1 ) + γ 2 Q ( s t + 2 ) + γ 3 Q ( s t + 3 ) . . . − Q ( s , a ) ] Q(s_t,a_t)+= \alpha[ r_t + \gamma Q(s_{t+1}) + \gamma^2 Q(s_{t+2})+ \gamma^3 Q(s_{t+3})... -Q(s,a) ] Q(st,at)+=α[rt+γQ(st+1)+γ2Q(st+2)+γ3Q(st+3)...−Q(s,a)]
代码实现上,是前几次不执行只是进行数据的收集,第n次开始进行多步Sarsa
5.4 Q-learning
Q ( s , a ) + = α [ r ( s , a ) + γ m a x a Q ( s , a ) − Q ( s , a ) ] Q(s,a) += \alpha[r(s,a) + \gamma max_aQ(s,a) - Q(s,a)] Q(s,a)+=α[r(s,a)+γmaxaQ(s,a)−Q(s,a)]
Q-learning的时序差分算法在算下一个状态的Q的时候会取最大的那个
Sarsa会先 ϵ − g r e e d y \epsilon -greedy ϵ−greedy 选择s,a然后计算TD_error,然后估计Q(s’,a’)(比如放在环境中跑一下)
Q-learning next_s和a之后,会找到最大的Q(s’,a’),不依赖于 ϵ − g r e e d y \epsilon -greedy ϵ−greedy 的a
-
在线策略算法和离线策略算法
在线策略算法:行为策略(采样数据的策略)和 目标策略(用于更新的策略)是同一个策略
离线策略算法:行为策略和目标策略并不是同一个策略
7 DQN算法
Q网络的损失函数
w ∗ = a r g m i n w 1 2 N ∑ i = 1 N [ r i + γ m a x i Q w ( s i ′ , a ′ ) − Q w ( s i , a i ) ] w^* = argmin_w \frac{1}{2N}\sum_{i=1}^N[r_i+\gamma max_i Q_w(s'_i,a') - Q_w(s_i,a_i)] w∗=argminw2N1i=1∑N[ri+γmaxiQw(si′,a′)−Qw(si,ai)]
-
经验回放
制作一个数据回放缓冲区,每次环境中得到的<s,a,r,s’>都进行存放
-
目标网络
采用TD_error作为我们的误差,但是包含着网络的输出,所以在更新网络参数的时候,目标也在不断地更新
因为优化目标是让
Q → r + γ m a x Q ( s ′ + a ′ ) Q \rightarrow r+\gamma max Q(s'+a') Q→r+γmaxQ(s′+a′)
相关文章:

强化学习算法总结 2
强化学习算法总结 2 4.动态规划 待解决问题分解成若干个子问题,先求解子问题,然后得到目标问题的解 需要知道整个状态转移函数和价值函数,状态空间离散且有限 策略迭代: 策略评估:贝尔曼期望方程来得到一个策略的 V ( s ) V(s…...

修改node_modules避免更新覆盖 patch-package
说明:直接修改第三方库的代码,会带来团队协作的问题,使用patch-package生成补丁包 什么是 patch-package? patch-package 是一个基于 Git 的工具,它可以帮助我们对依赖包进行修复补丁。通过创建一个与问题相关的补丁文…...
Elasticsearch安装,Springboot整合Elasticsearch详细教程
Elasticsearch 是一个分布式、RESTful 风格的搜索和数据分析引擎,能够实现近乎实时的搜索。 Elasticsearch官网https://www.elastic.co/cn/ 这篇文章主要简单介绍一下Elasticsearch,Elasticsearch的java API博主也在学习中,文章会持续更新~ …...
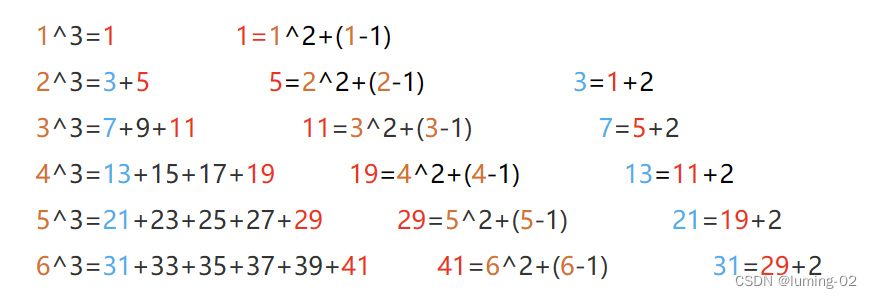
OJ题库:计算日期到天数转换、打印从1到最大的n位数 、尼科彻斯定理
前言:在部分大厂笔试时经常会使用OJ题目,这里对《华为机试》和《剑指offer》中的部分题目进行思路分析和讲解,希望对各位读者有所帮助。 题目来自牛客网,欢迎各位积极挑战: HJ73:计算日期到天数转换_牛客网 JZ17:打印…...
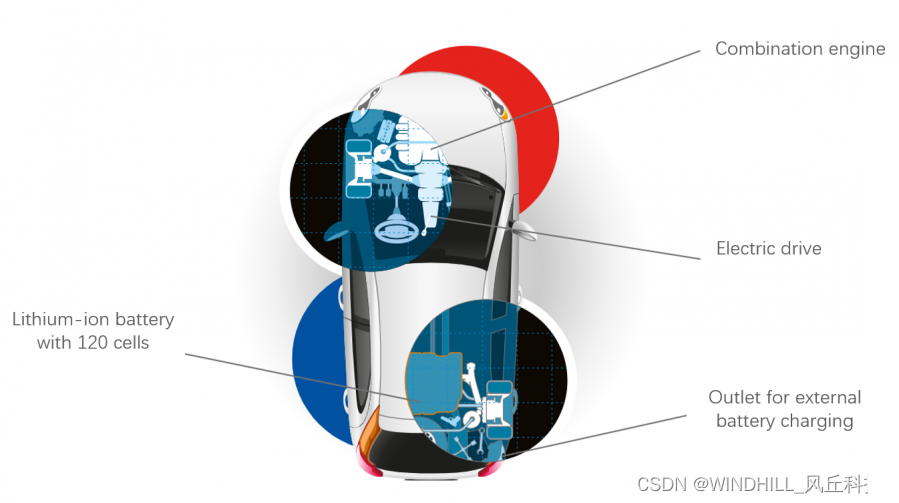
混合动力汽车耐久测试
一 背景 整车厂可通过发动机和电机驱动的结合为多款车型提供混合动力驱动技术。汽车集成电机驱动可大大减少二氧化碳的排放,不仅如此,全电动驱动或混合动力驱动的汽车还将使用户体验到更好的驾驶感受,且这种汽车可通过电动机来实现更快的加速…...
useRef 定义的 ref 在控制台可以打印但是页面不生效?
useRef 是一个 React Hook,它能让你引用一个不需要渲染的值。 点击计时器 点击按钮后在控制台可以打印但是页面不生效。 useRef 返回的值在函数组件中不会自动触发重新渲染,所以控制台可以显示变化而按钮上无法显示 ref.current的变化。 import { use…...
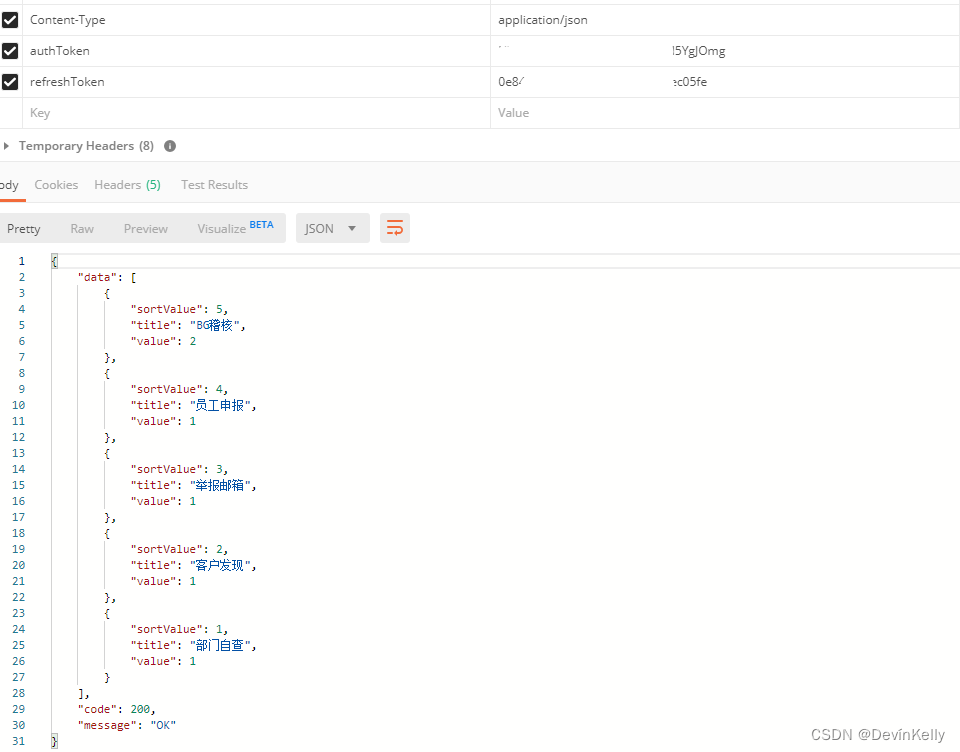
【Java 动态数据统计图】动态数据统计思路案例(动态,排序,动态数组(重点推荐))七(129)
需求:前端根据后端的返回数据:画统计图; 说明: 1.X轴为地域,Y轴为地域出现的次数; 2. 动态展示(有地域展示,没有不展示,且高低排序) Demo案例: …...

Cell Reports | 揭开METTL14在介导m6A修饰中的神秘面纱
m6A被认为是最丰富的mRNA修饰,广泛分布在大多数真核生物中,包括哺乳动物、植物、昆虫、酵母和某些病毒。m6A修饰的沉积和去除之间的动态平衡对于正常的生物过程和发育至关重要,如失调通常与癌症等疾病有关。m6A修饰由m6A甲基转移酶复合物&…...

297. 二叉树的序列化与反序列化
题目描述 序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。 请设计一个算法来实现二叉树的序列化与反序…...
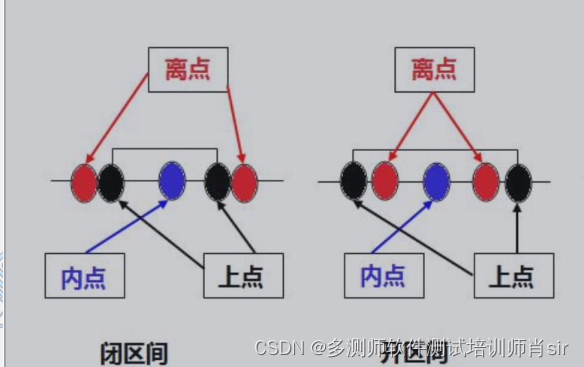
肖sir__设计测试用例方法之边界值03_(黑盒测试)
设计测试用例方法之边界值 边界点定义 上点:边界上的点 离点:离上点最近的点(即上点左右两边最邻近的点) 内点:在域范围内的点 案例:qq号:5-12位 闭区间: 离点:5 位 &…...

功能测试常用的测试用例大全
登录、添加、删除、查询模块是我们经常遇到的,这些模块的测试点该如何考虑 1)登录 ① 用户名和密码都符合要求(格式上的要求) ② 用户名和密码都不符合要求(格式上的要求) ③ 用户名符合要求,密码不符合要求(格式上的要求) ④ 密码符合要求,…...

css利用flex分配剩余高度出现子组件溢出问题
1.利用flex分配剩余高度/宽度 情景:父组件高度一定,子组件中,其他子组件高度固定,一个子组件高度不确定(页面滚动列表) .father{display: flex;flex-direction: column;.son1{height: 200px;}.son2{//或 …...
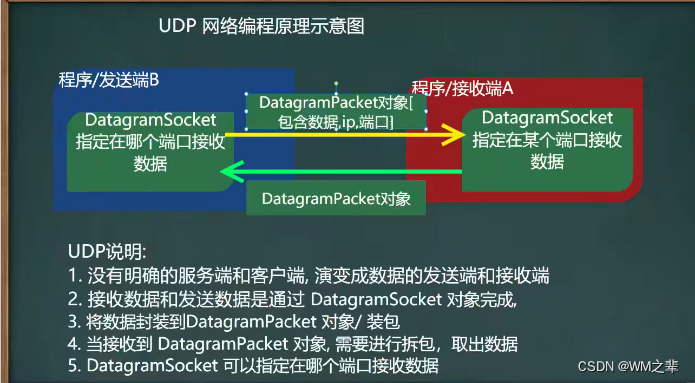
Java中的网络编程------基于Socket的TCP编程和基于UDP的网络编程,netstat指令
Socket 在Java中,Socket是一种用于网络通信的编程接口,它允许不同计算机之间的程序进行数据交换和通信。Socket使得网络应用程序能够通过TCP或UDP协议在不同主机之间建立连接、发送数据和接收数据。以下是Socket的基本介绍: Socket类型&…...

【【STM32-29正点原子版本串口发送传输实验】
STM32-29正点原子版本串口发送传输实验 通过串口接收或发送一个字符 例程目的 开发板上我们接入的是实现异步通信的UART接口 USB转串口原理图 我们一步步分析 PA9是串口1 的发送引脚 PA10是串口1 的接受引脚 。因为我们现在只是用到异步收发器功能,所以我们现…...

【面试题精讲】什么是websocket?如何与前端通信?
有的时候博客内容会有变动,首发博客是最新的,其他博客地址可能会未同步,认准https://blog.zysicyj.top 首发博客地址 系列文章地址 什么是WebSocket? WebSocket是一种在Web应用程序中实现双向通信的协议。它允许在客户端和服务器之间建立持久…...
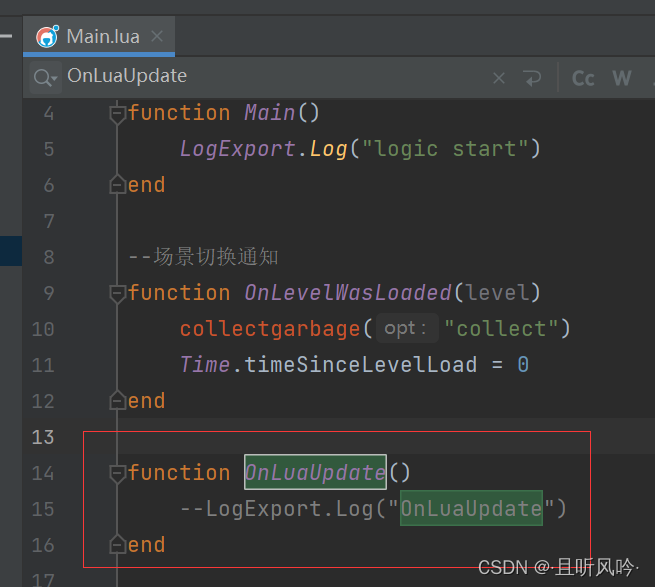
unity tolua热更新框架教程(2)
Lua启动流程 增加脚本luamain,继承luaclient 建立第一个场景GameMain,在对象GameMain挂载脚本LuaMain,启动场景 看到打印,lua被成功加载 lua入口及调用堆栈 这里会执行main.lua文件的main函数 C#接口导出 在此处配置C#导出的代码 …...
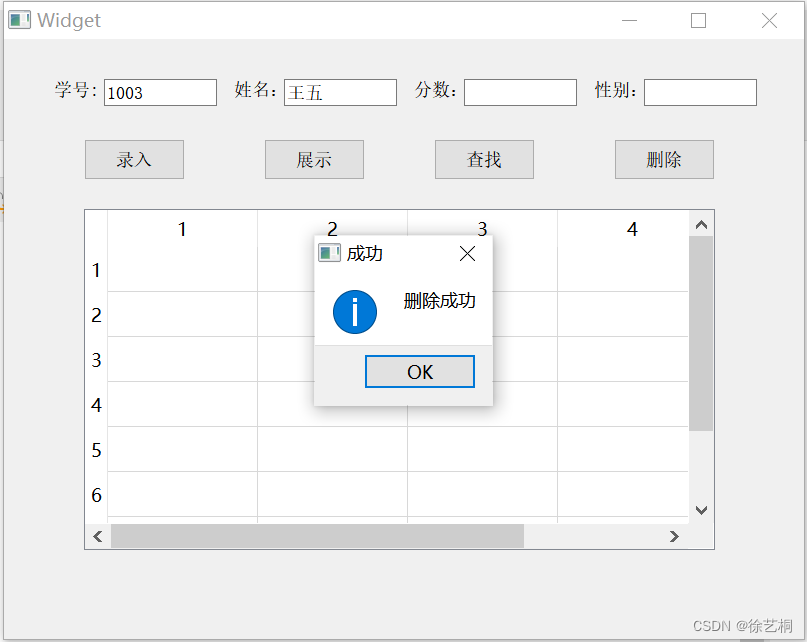
【0904作业】QT 完成登陆界面跳转到聊天室+完成学生管理系统的查找和删除功能
一、完成登陆界面跳转到聊天室 1> 项目结构 2> 源码 ① .pro ②main #include "mywnd.h" #include"chatCli.h" #include <QApplication>int main(int argc, char *argv[]) {QApplication a(argc, argv);MyWnd w;w.show();Form f;QObject::co…...

ceph源码阅读 buffer
ceph::buffer是ceph非常底层的实现,负责管理ceph的内存。ceph::buffer的设计较为复杂,但本身没有任何内容,主要包含buffer::list、buffer::ptr、buffer::hash。这三个类都定义在src/include/buffer.h和src/common/http://buffer.cc中。 buffe…...

基本介绍——数据挖掘
1.数据挖掘的定义 数据挖掘是采用数学的、统计的、人工智能和神经网络等领域的科学方法,如记忆推理、聚类分析、关联分析、决策树、神经网络、基因算法等技术,从大量数据中挖掘出隐含的、先前未知的、对决策有潜在价值的关系、模式和趋势,并…...

Navicat连接postgresql时出现‘datlastsysoid does not exist‘报错
当使用 Navicat 连接 PostgreSQL 数据库时出现 ‘datlastsysoid does not exist’ 的错误报错,这可能是由于 Navicat 版本与 PostgreSQL 版本不兼容所致。 这是因为在较新的 PostgreSQL 版本中移除了 ‘datlastsysoid’ 列,但可能较旧版本的 Navicat 尚…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
