现代C++中的从头开始深度学习:【6/8】成本函数
现代C++中的从头开始深度学习:成本函数

一、说明
在机器学习中,我们通常将问题建模为函数。因此,我们的大部分工作都包括寻找使用已知模型近似函数的方法。在这种情况下,成本函数起着核心作用。
这个故事是我们之前关于卷积的讨论的续集。今天,我们将介绍成本函数的概念,展示常见示例并学习如何编码和绘制它们。与往常一样,从头开始纯C++和本征。
二、关于本系列
在本系列中,我们将学习如何仅使用普通和现代C++对必须知道的深度学习算法进行编码,例如卷积、反向传播、激活函数、优化器、深度神经网络等。

这个故事是:C++中的成本函数
现代C++中的从头开始深度学习【3/8】:激活函数
现代C++中的从头开始深度学习:【4/8】梯度下降
现代C++中的从头开始深度学习:【5/8】卷积
...更多内容即将推出。
三、机器学习中的建模
作为人工智能工程师,我们通常将每个任务或问题定义为一个功能。
例如,如果我们正在开发一个人脸识别系统,我们的第一步是将问题定义为将输入图像映射到标识符的函数:

对于医疗诊断系统,我们可以定义一个函数来将症状映射到诊断:

我们可以编写一个模型来提供给定单词序列的图像:
这是一个无穷无尽的清单。使用函数来表示任务或问题是实现机器学习系统的简化方法。
问题往往是:如何知道 F() 公式?
四、近似函数
事实上,使用公式或规则序列定义F(X)是不可行的(有一天我将解释原因)。
一般来说,我们不是找到或定义正确的函数 F(X),而是尝试找到 F(X) 的近似值。 让我们通过假设函数来称这种近似,或者简单地称为H(X)。
乍一看,这没有意义:如果我们需要找到近似函数 H(X),为什么我们不尝试直接找到 F(X)?
答案是:我们知道H(X)。虽然我们对F(X)知之甚少,但我们几乎知道H(X)的一切:它的公式,参数等。关于 H(X),我们唯一不知道的是它的参数值。
事实上,机器学习的主要关注点是找到为给定问题和数据确定合适参数值的方法。让我们看看我们如何执行它。
在机器学习术语中,H(X)被称为“F(X)的近似值”。H(X)的存在被通用近似定理所涵盖。
五、成本函数和通用逼近定理
考虑这样一种情况:我们知道输入的值和相应的输出,但我们不知道 的公式。例如,我们知道如果输入是,那么结果就是。XY = F(X)F(X)X = 1.0F(1.0)Y = 2.0
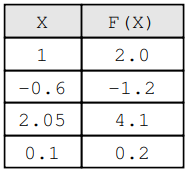
4 X 和 F(X) 的映射
现在,考虑我们有一个已知的函数,我们想知道是否是 的良好近似。因此,我们计算并找到.H(X)H(X)F(X)T = H(1.0)T = 1.9
这个值有多糟糕,因为我们知道真正的值是什么时候?T = 1.9Y = 2.0X = 1.0
用于量化 和 之间的差额的成本的指标由成本函数调用。YT
请注意,Y 是期望值,T 是我们猜测获得的实际值
H(X)
成本函数的概念是机器学习的核心。让我们以最常见的成本函数为例。
六、均方误差
最著名的成本函数是均方误差:
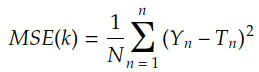
其中 Ti 由核 k 对 Xi 的卷积给出:
![]()
我们在上一个故事中讨论了卷积
请注意,我们有 n 对 (Yn, T n),每对都是期望值 Yi 和实际值 Tn 的组合。例如:
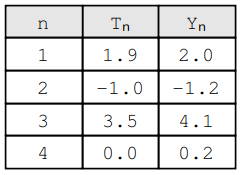
因此,MSE 的评估如下:
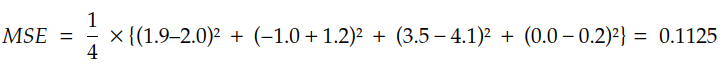
我们可以编写MSE的第一个版本,如下所示:
auto MSE = [](const std::vector<double> &Y_true, const std::vector<double> &Y_pred) {if (Y_true.empty()) throw std::invalid_argument("Y_true cannot be empty.");if (Y_true.size() != Y_pred.size()) throw std::invalid_argument("Y_true and Y_pred sizes do not match.");auto quadratic = [](const double a, const double b) {double result = a - b;return result * result;};const int N = Y_true.size();double acc = std::inner_product(Y_true.begin(), Y_true.end(), Y_pred.begin(), 0.0, std::plus<>(), quadratic);double result = acc / N;return result;
};现在我们知道了如何计算MSE,让我们看看如何使用它来近似函数。
七、使用MSE找到最佳参数的直觉
假设我们有一个映射 F(X) 合成生成:
F(X) = 2*X + N(0, 0.1)其中 N(0, 0.1) 表示从正态分布中抽取的随机值,平均值 = 0,标准差 = 0.1。我们可以通过以下方式生成示例数据:
#include <random>std::default_random_engine dre(time(0));std::normal_distribution<double> gaussian_dist(0., 0.1);
std::uniform_real_distribution<double> uniform_dist(0., 1.);std::vector<std::pair<double, double>> sample(90);std::generate(sample.begin(), sample.end(), [&gaussian_dist, &uniform_dist]() {double x = uniform_dist(dre);double noise = gaussian_dist(dre);double y = 2. * x + noise;return std::make_pair(x, y);
});如果我们使用任何电子表格软件绘制此示例,我们会得到如下所示的内容:
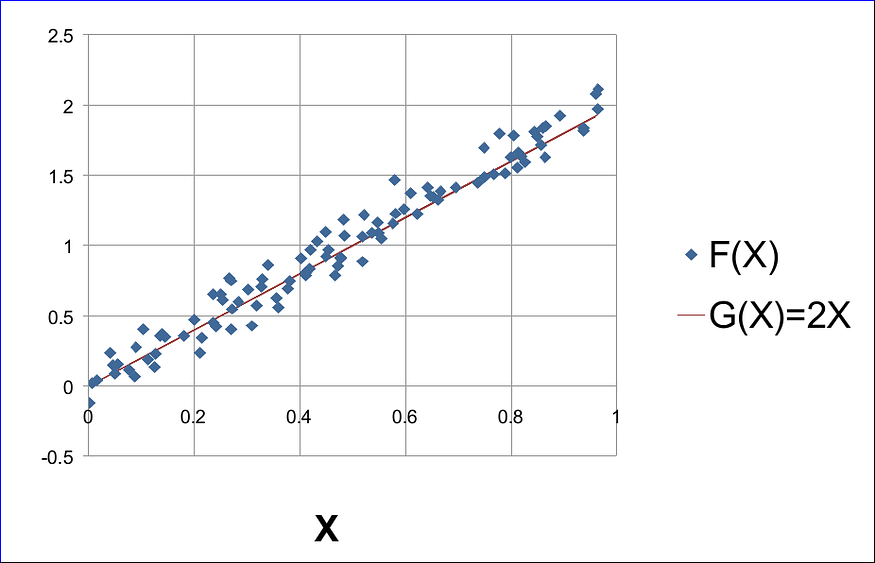
请注意,我们知道 G(X) 和 F(X) 的公式。然而,在现实生活中,这些生成器功能是潜在现象的未公开秘密。在这里,在我们的示例中,我们只知道它们,因为我们正在生成合成数据来帮助我们更好地理解。
在现实生活中,我们所知道的一切都是一个假设,即由H(X)= kX定义的假设函数H(X)可能是F(X)的良好近似值。 当然,我们还不知道k的值是多少。
让我们看看如何使用 MSE 找出合适的 k 值。事实上,它就像为一系列不同的 k 绘制 MSE 一样简单:
std::vector<std::pair<double, double>> measures;double smallest_mse = 1'000'000'000.;
double best_k = -1;
double step = 0.1;for (double k = 0.; k < 4.1; k += step) {std::vector<double> ts(sample.size());std::transform(sample.begin(), sample.end(), ts.begin(), [k](const auto &pair) {return pair.first * k;});double mse = MSE(ys, ts);if (mse < smallest_mse) {smallest_mse = mse;best_k = k;}measures.push_back(std::make_pair(k, mse));
}std::cout << "best k was " << best_k << " for a MSE of " << smallest_mse << "\n";很多时候,这个程序输出的东西是这样的:
best k was 2.1 for a MSE of 0.00828671
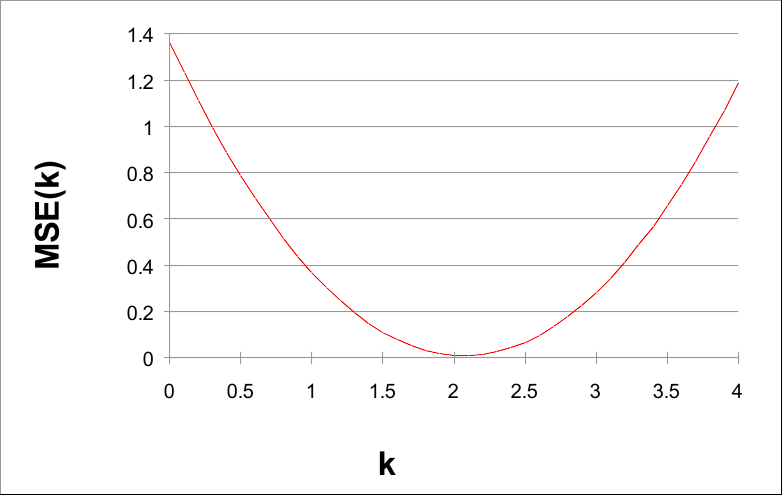
如果我们用k绘制MSE(k),我们可以看到一个非常有趣的事实:
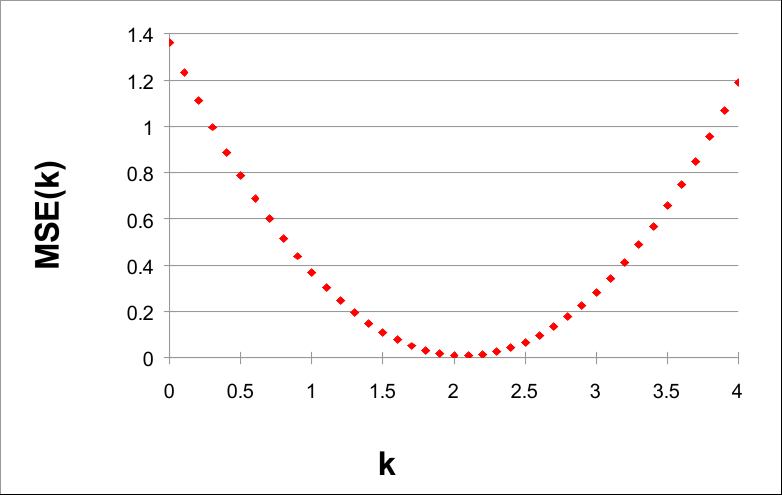
k 从 0 到 4,步长为 0.1
请注意,MSE(k) 的值在 k = 2 附近最小。实际上,2 是泛型函数 G(X) = 2X 的参数。
给定数据并使用 0.1 的步长,当 k = 2.1 时,可以找到较小的 MSE(k) 值。这表明 H(X) = 2.1 X 是 F(X) 的良好近似值。 事实上,如果我们绘制F(X)、G(X)和H(X),我们有:
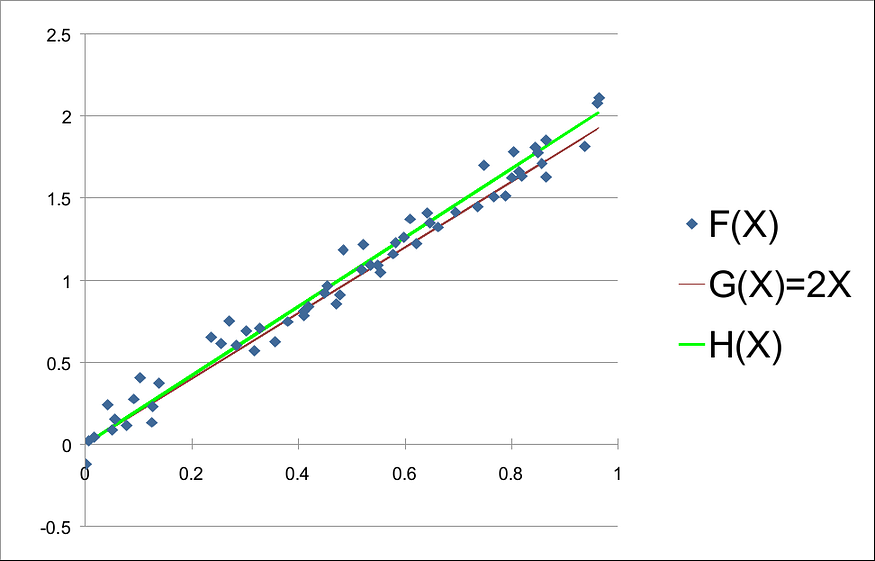
通过上面的图表,我们可以意识到H(X)实际上近似于F(X)。不过,我们可以尝试使用较小的步长(如 0.01 或 0.001)来找到更好的近似值。
代码可以在此存储库中找到
八、成本表面
MSE(k) 乘以 k 的曲线是成本曲面的一维示例。
前面的示例显示的是,我们可以使用成本表面的最小值来找到参数 k 的最佳拟合值。
该示例描述了机器学习中最重要的范式:通过成本函数最小化的函数近似。
上图显示了一个一维成本曲面,即给定一维k的成本曲线。在二维空间中,即当我们有两个k,即k1和k2时,成本面看起来更像一个实际曲面:
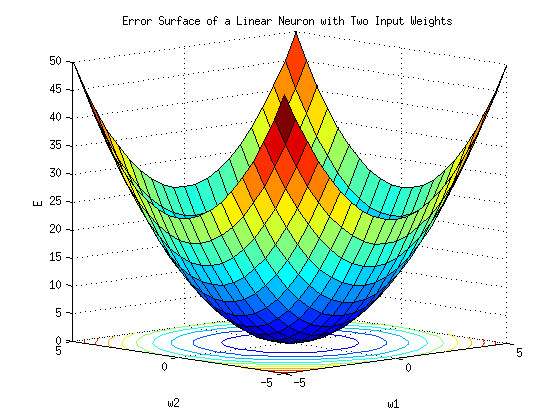
无论 k 是 1D、2D 还是更高维,找到最佳第 k 个值的过程都是相同的:找到成本曲线的最小值。
最小成本值也称为全局最小值。
在 1D 空间中,查找全局最小值的过程相对容易。然而,在高维度上,扫描所有空间以找到最小值可能会产生计算成本。在下一个故事中,我们将介绍大规模执行此搜索的算法。
不仅k可以是高维的。在实际问题中,输出通常也是高维的。让我们学习如何在这种情况下计算 MSE。
九、高维输出上的MSE
在现实世界的问题中,Y 和 T 是向量或矩阵。让我们看看如何处理这样的数据。
如果输出是一维的,则MSE的先前公式将起作用。但是如果输出是多维的,我们需要稍微改变一下公式。例如:
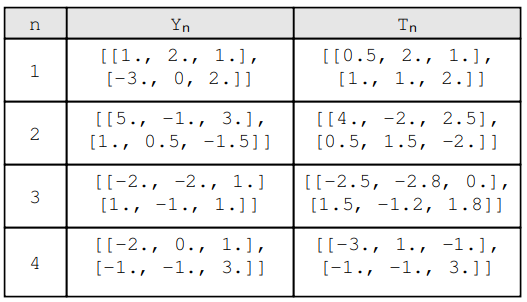
在这种情况下,Yn 和 Tn 不是标量值,而是大小矩阵。在将 MSE 应用于此数据之前,我们需要更改公式,如下所示:(2,3)

在此公式中,N 是对数,R 是行数,C 是每对中的列数。像往常一样,我们可以使用 lambda 实现此版本的 MSE:
#include <numeric>
#include <iostream>#include <Eigen/Core>using Eigen::MatrixXd;int main()
{auto MSE = [](const std::vector<MatrixXd> &Y_true, const std::vector<MatrixXd> &Y_pred) {if (Y_true.empty()) throw std::invalid_argument("Y_true cannot be empty.");if (Y_true.size() != Y_pred.size()) throw std::invalid_argument("Y_true and Y_pred sizes do not match.");const int N = Y_true.size();const int R = Y_true[0].rows();const int C = Y_true[0].cols();auto quadratic = [](const MatrixXd a, const MatrixXd b) {MatrixXd result = a - b;return result.cwiseProduct(result).sum();};double acc = std::inner_product(Y_true.begin(), Y_true.end(), Y_pred.begin(), 0.0, std::plus<>(), quadratic);double result = acc / (N * R * C);return result;};std::vector<MatrixXd> A(4, MatrixXd::Zero(2, 3)); A[0] << 1., 2., 1., -3., 0, 2.;A[1] << 5., -1., 3., 1., 0.5, -1.5; A[2] << -2., -2., 1., 1., -1., 1.; A[3] << -2., 0., 1., -1., -1., 3.;std::vector<MatrixXd> B(4, MatrixXd::Zero(2, 3)); B[0] << 0.5, 2., 1., 1., 1., 2.; B[1] << 4., -2., 2.5, 0.5, 1.5, -2.; B[2] << -2.5, -2.8, 0., 1.5, -1.2, 1.8; B[3] << -3., 1., -1., -1., -1., 3.5;std::cout << "MSE: " << MSE(A, B) << "\n";return 0;
}
值得注意的是,无论 k 或 Y 是多维的还是不是多维的,MSE 始终是一个标量值。
十、其他成本函数
除了MSE,深度学习模型中也经常出现其他成本函数。最常见的是分类交叉熵、对数 cosh 和余弦相似性。
我们将在接下来的故事中介绍这些功能,特别是当我们介绍分类和非线性推理时。
十一、结论和下一步
成本函数是机器学习中最重要的主题之一。在这个故事中,我们学习了如何编写最常用的成本函数MSE代码,以及如何使用它来适应一维问题。我们还了解了为什么成本函数对于查找函数近似如此重要。
在下一个故事中,我们将学习如何使用成本函数从数据中训练卷积核。我们将介绍拟合内核的基本算法,并讨论训练机制的实现,例如 epoch、停止条件和超参数
相关文章:

现代C++中的从头开始深度学习:【6/8】成本函数
现代C中的从头开始深度学习:成本函数 一、说明 在机器学习中,我们通常将问题建模为函数。因此,我们的大部分工作都包括寻找使用已知模型近似函数的方法。在这种情况下,成本函数起着核心作用。 这个故事是我们之前关于卷积的讨论的…...

Vue——vue3中的ref和reactive数据理解以及父子组件之间props传递的数据
ref()函数 这是一个用来接受一个内部值,返回一个响应式的、可更改的 ref 对象,此对象只有一个指向其内部值的属性 .value。 作用:创建一个响应式变量,使得某个变量在发生改变时可以同步发生在页面上。 模板语句中使用这个变量时…...

新手如何备考PMP考试?
回头看来,从战略上来说: 备考第一重点:要有一个清晰的目标——我要过! 第二重点:足够重视它——把它的优先级调整到仅次于工作:万籁俱寂,唯有学习。 第三重点:自律——有了第一点…...

FPGA输出lvds信号点亮液晶屏
1 概述 该方案用于生成RGB信号,通过lvds接口驱动逻辑输出,点亮并驱动BP101WX-206液晶屏幕。 参考:下面为参考文章,内容非常详细。Xilinx LVDS Output——原语调用_vivado原语_ShareWow丶的博客http://t.csdn.cn/Zy37p 2 功能描述 …...
算法面试-深度学习基础面试题整理(2023.8.29开始,每天下午持续更新....)
一、无监督相关(聚类、异常检测) 1、常见的距离度量方法有哪些?写一下距离计算公式。 1)连续数据的距离计算: 闵可夫斯基距离家族: 当p 1时,为曼哈顿距离;p 2时,为欧…...
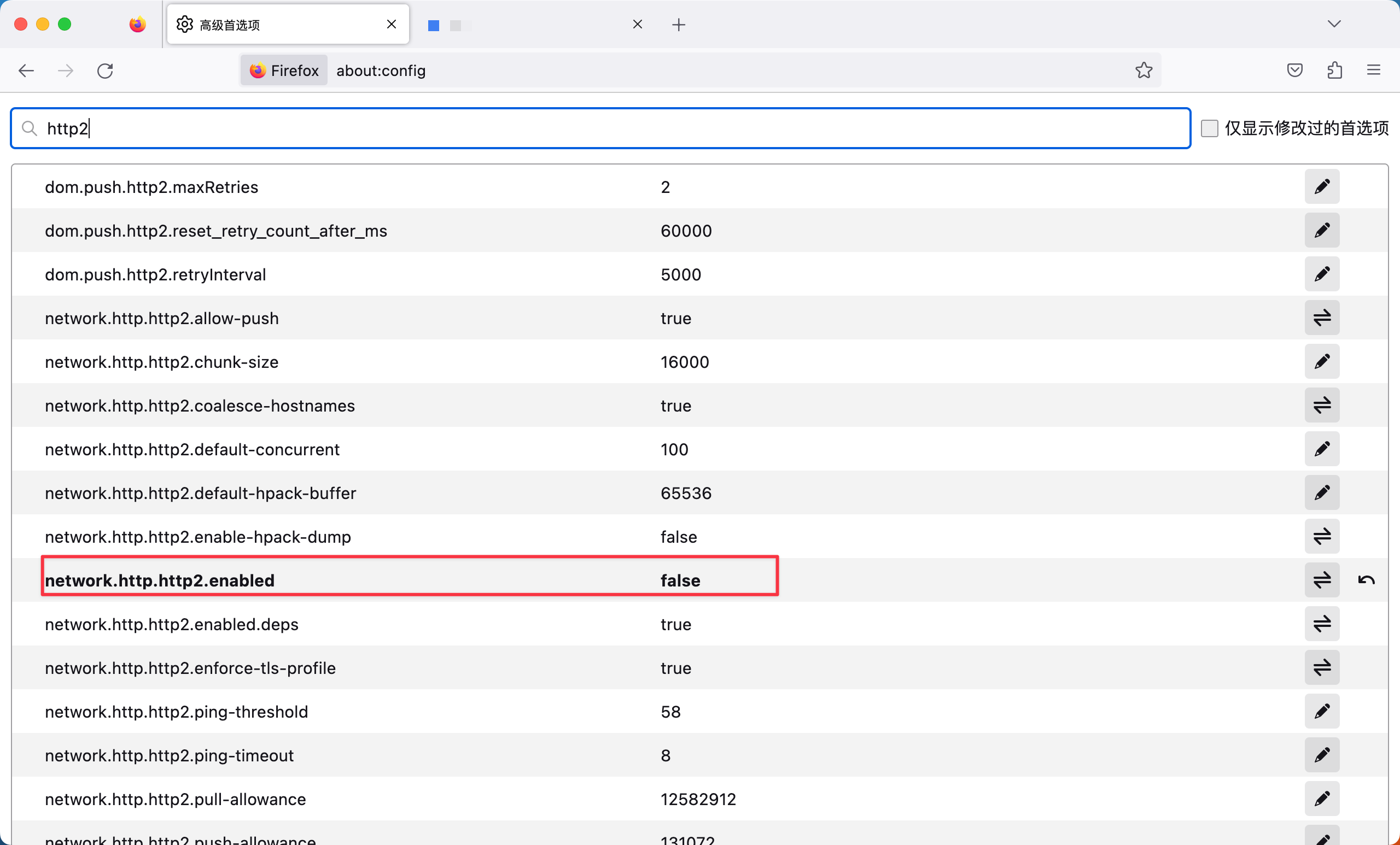
FireFox禁用HTTP2
问题 最近需要调试接口,但是,Chrome都是强制使用h2协议,即HTTP/2协议。为了排除h2协议排除对接口调用的影响,需要强制浏览器使用HTTP1协议。 解决 FireFox 设置firefox的network.http.http2.enabled为禁用,这样就禁…...

搭建HTTPS服务器
HTTPS代理服务器的作用与价值 HTTPS代理服务器可以帮助我们实现网络流量的转发和加密,提高网络安全性和隐私保护。本文将指导您从零开始搭建自己的HTTPS代理服务器,让您更自由、安全地访问互联网。 1. 准备工作:选择服务器与操作系统 a. 选…...

无人化在线静电监控系统的组成
无人化在线静电监控系统是一种用于检测和监控静电情况的系统,它可以自动地实时监测各个区域的静电水平,并在出现异常情况时发出报警信号。静电监控报警器则是该系统中的一个重要组成部分,用于接收和传达报警信号。 无人化在线静电监控系统通…...

element ui级联选择器数据处理
后端同事返回的级联选择器数据的children是childrens,而组件渲染只识别children,所以需要props自定义传入,代码如下 <el-form-item label"应用页面:" prop"appId"><el-cascader:props"{ child…...

zookeeper-3.6.4集群搭建
1、上传zookeeper安装包并解压 上传路径:/opt/software/ 解压路径:/opt/module/ 2、创建数据目录及日志目录 #数据目录:/data/zookeeper/data/ #3台机器创建存储目录: sudo mkdir -p /data/zookeeper/data#日志目录:…...

15种下载文件的方法文件下载方法汇总超大文件下载
15种下载文件的方法&文件下载方法汇总&超大文件下载 15种下载文件的方法Pentesters经常将文件上传到受感染的盒子以帮助进行权限提升,或者保持在计算机上的存在。本博客将介绍将文件从您的计算机移动到受感染系统的15种不同方法。对于那些在盒子上存在且需要…...
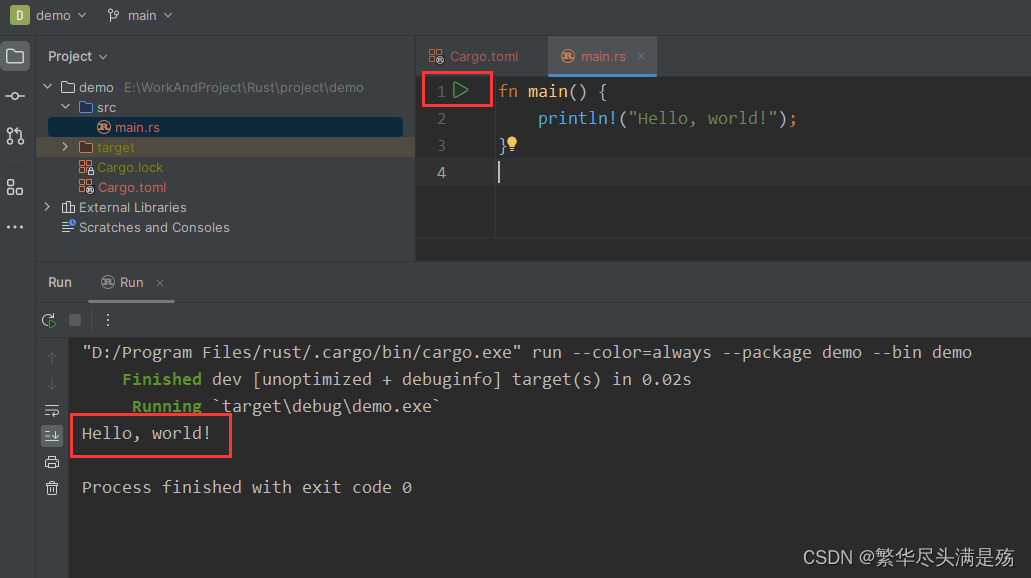
Windows安装配置Rust(附CLion配置与运行)
Windows安装配置Rust(附CLion配置与运行) 前言一、下载二、安装三、配置标准库!!!四、使用 CLion 运行 rust1、新建rust项目2、配置运行环境3、运行 前言 本文以 windows 安装为例,配置编译器为 minGW&…...

【ROS】例说mapserver静态地图参数(对照Rviz、Gazebo环境)
文章目录 例说mapserver静态地图参数1. Rviz中显示的地图2. mapserver保存地图详解3. 补充实验 例说mapserver静态地图参数 1. Rviz中显示的地图 在建图过程中,rviz会显示建图的实时情况,其输出来自于SLAM,浅蓝色区域为地图大小,…...
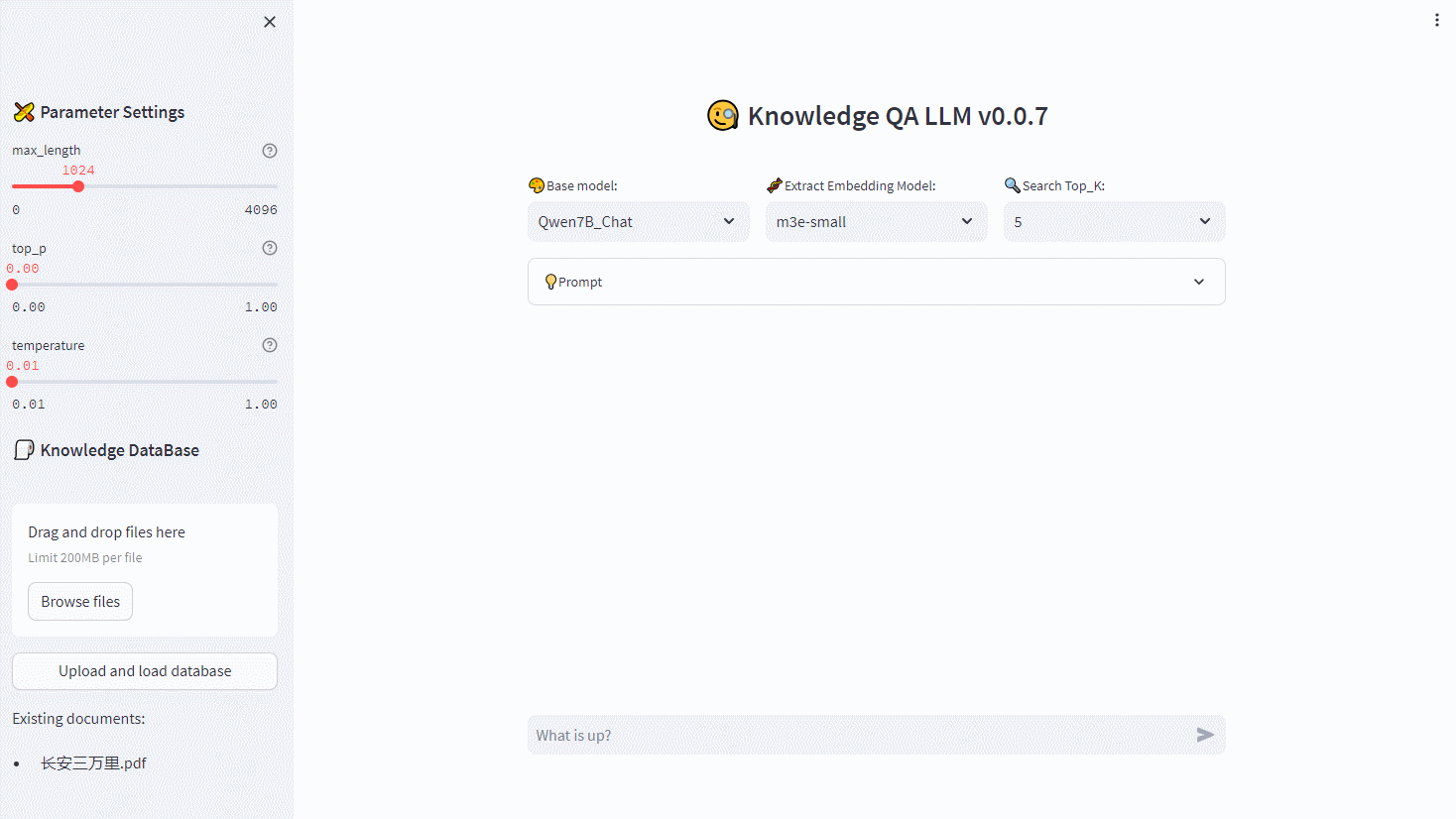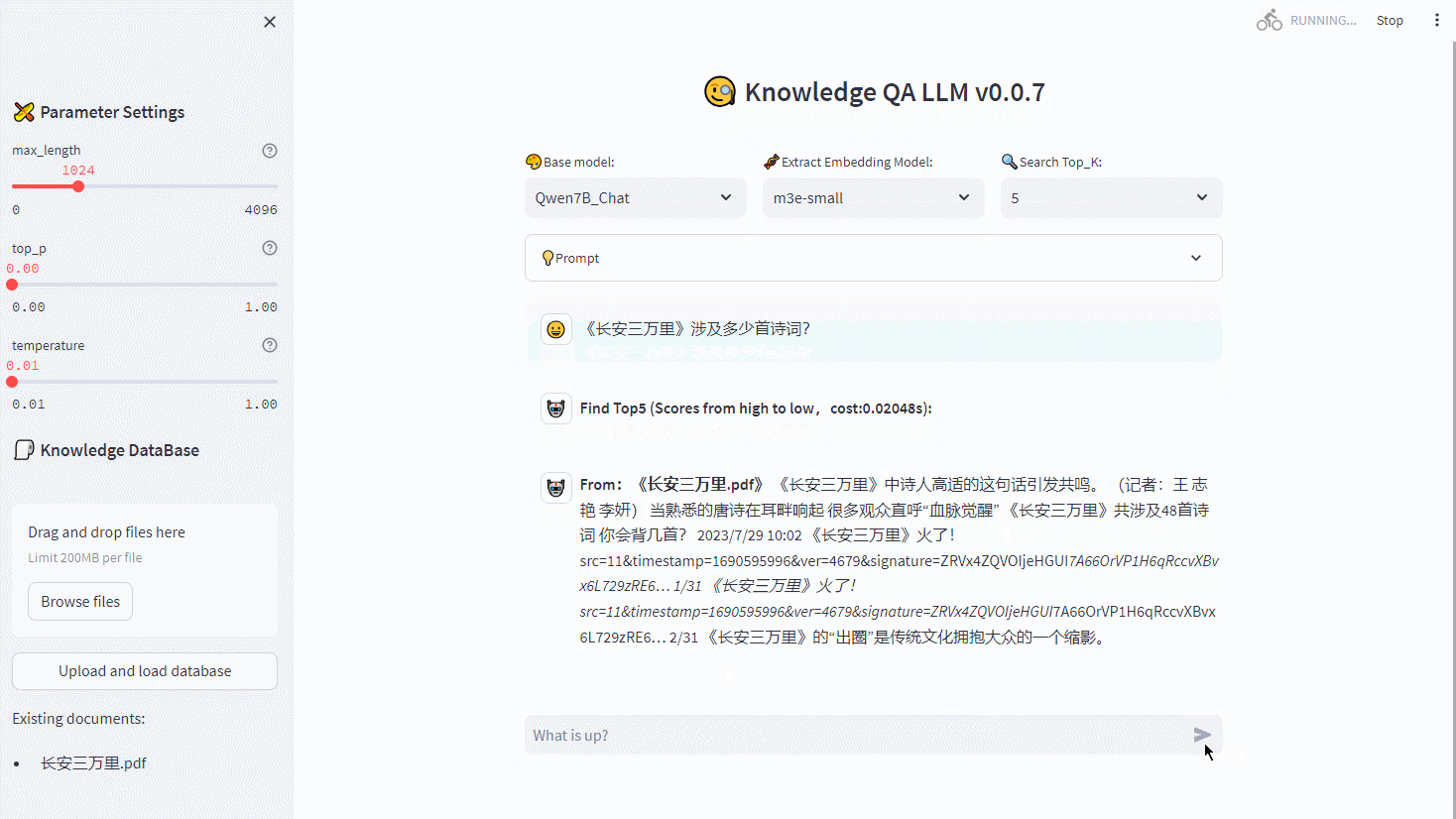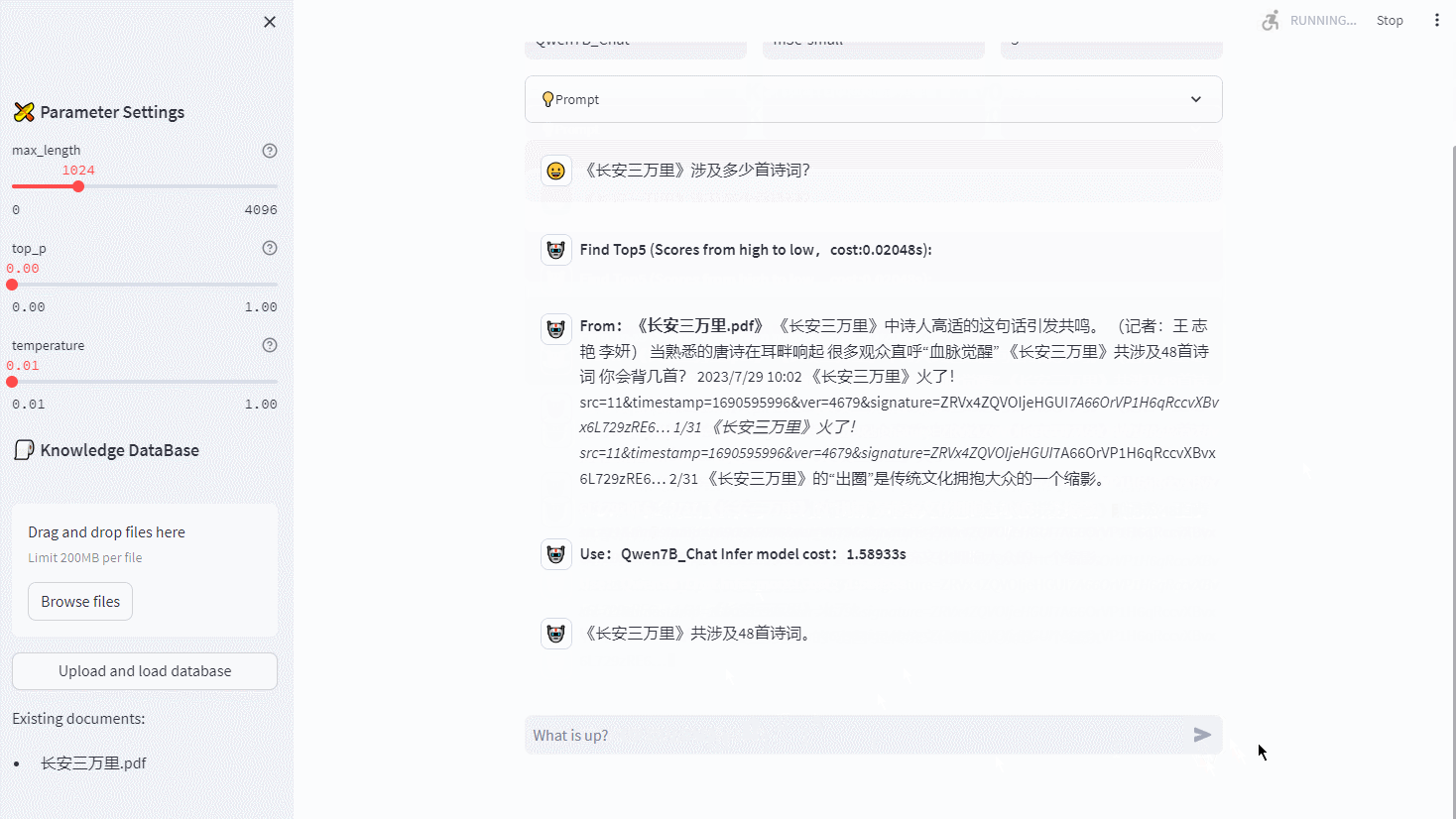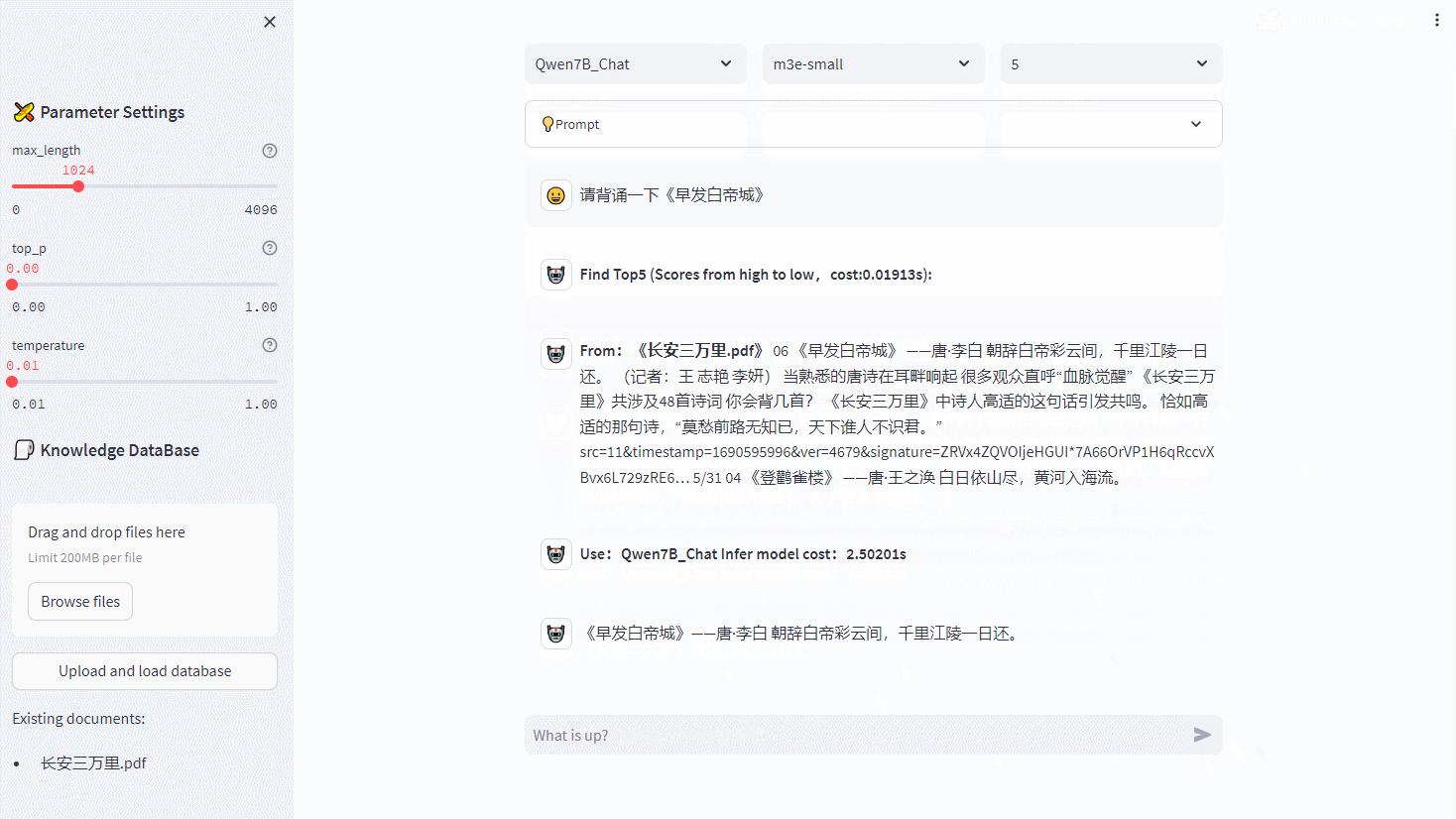
【RapidAI】P0 项目总览
RapidAI 项目总览 ** 内容介绍 ** Author: SWHL、omahs Github: https://github.com/RapidAI/Knowledge-QA-LLM/ CSDN Author: 脚踏实地的大梦想家 UI Demo: ** 读者须知 ** 本系列博文,主要内容为将 RapidAI 项目逐…...
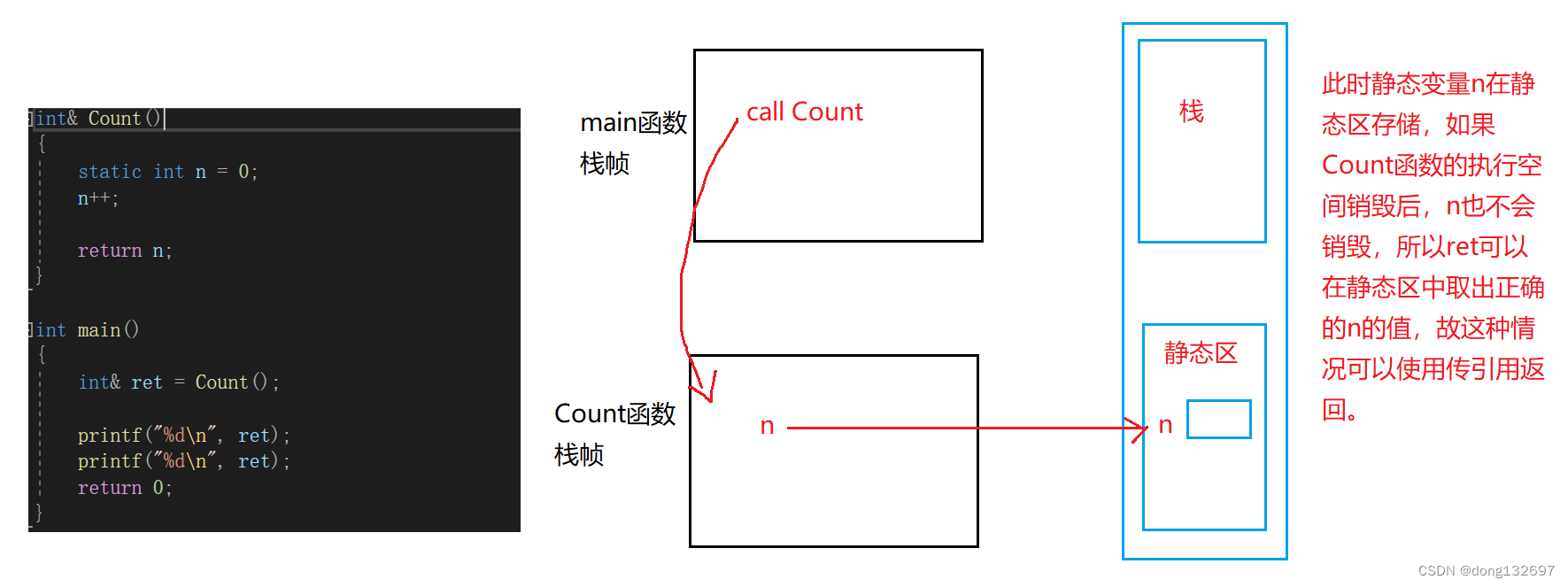
初识c++
文章目录 前言一、C命名空间1、命名空间2、命名空间定义 二、第一个c程序1、c的hello world2、std命名空间的使用惯例 三、C输入&输出1、c输入&输出 四、c中缺省参数1、缺省参数概念2、缺省参数分类3、缺省参数应用 五、c中函数重载1、函数重载概念2、函数重载应用 六、…...

【面试经典150题】跳跃游戏Ⅱ
题目链接 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i]i j < n 返回到达 nums[n…...

20230831-完成登录框的按钮操作,并在登录成功后进行界面跳转
登录框的按钮操作,并在登录成功后进行界面跳转 app.cpp #include "app.h" #include <cstdio> #include <QDebug> #include <QLineEdit> #include <QLabel> #include <QPainter> #include <QString> #include <Q…...

039 - sql逻辑操作符
前提: 做两个表employee和movie,用来练习使用; 表一:employee -- 创建表employee CREATE TABLE IF NOT EXISTS employee(id INT NOT NULL AUTO_INCREMENT,first_name VARCHAR(100) NOT NULL,last_name VARCHAR(100) NOT NULL,t…...

DbLInk使用
DbLInk介绍 DbLink是一种数据库连接技术,在不同的数据库之间进行数据传输和共享。它提供了一种透明的方法,让一个数据库访问另一个数据库的数据。 DbLink的优点是可以在多个数据库间实现数据共享,并且为不同数据库间的数据访问提供了便捷的…...

2.3 Vector 动态数组(迭代器)
C数据结构与算法 目录 本文前驱课程 1 C自学精简教程 目录(必读) 2 Vector<T> 动态数组(模板语法) 本文目标 1 熟悉迭代器设计模式; 2 实现数组的迭代器; 3 基于迭代器的容器遍历; 迭代器语法介绍 对迭…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...
