当前位置： 首页 > news >正文

【STM32】学习笔记-时间戳RTC

news 2026/2/11 4:43:31

Unix时间戳

Unix 时间戳（Unix Timestamp）定义为从UTC/GMT的1970年1月1日0时0分0秒开始所经过的秒数，不考虑闰秒
时间戳存储在一个秒计数器中，秒计数器为32位/64位的整型变量
世界上所有时区的秒计数器相同，不同时区通过添加偏移来得到当地时间.
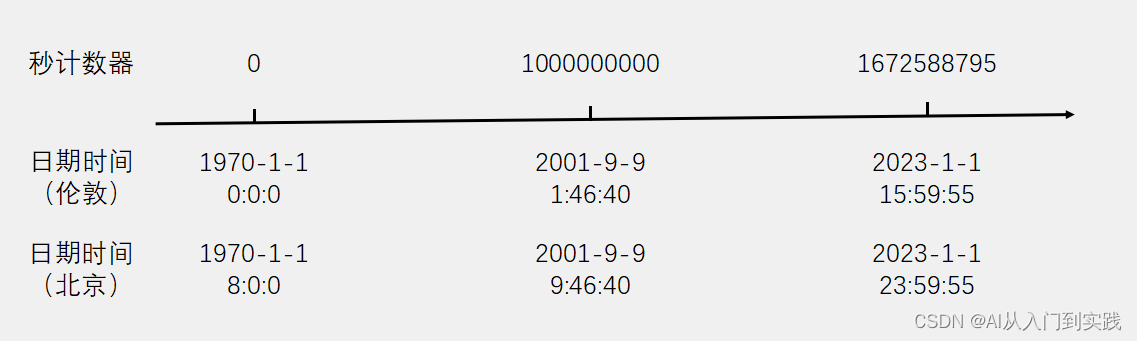
在这里插入图片描述

好处：时间间隔好；硬件电路使用；储存方便；
害处：消耗软件进程。
STM32是32位秒计数器。
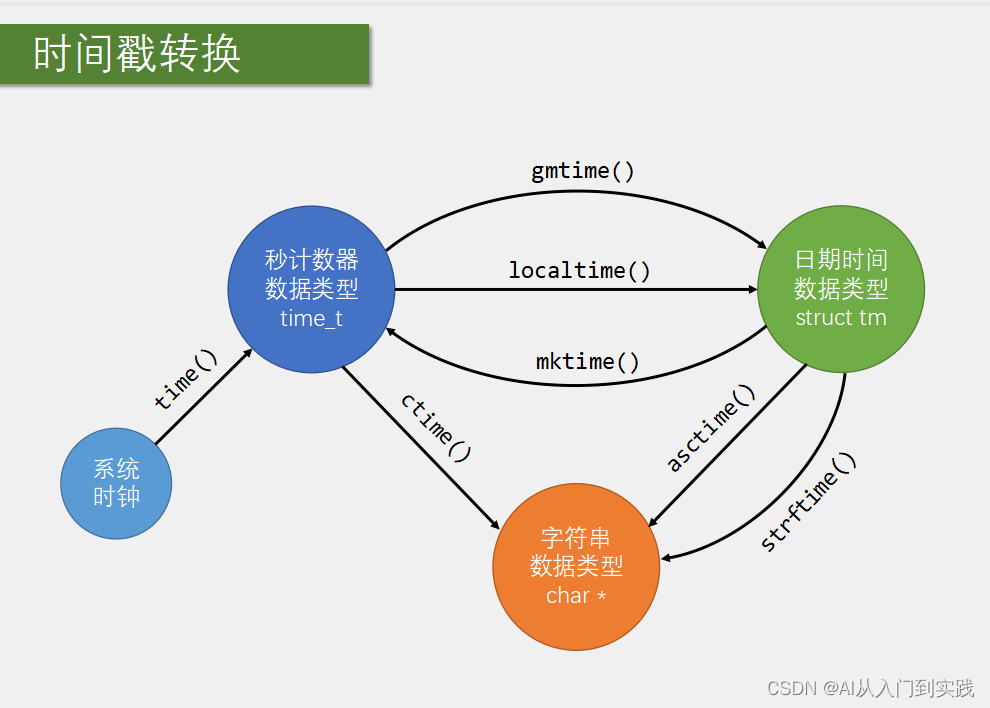
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

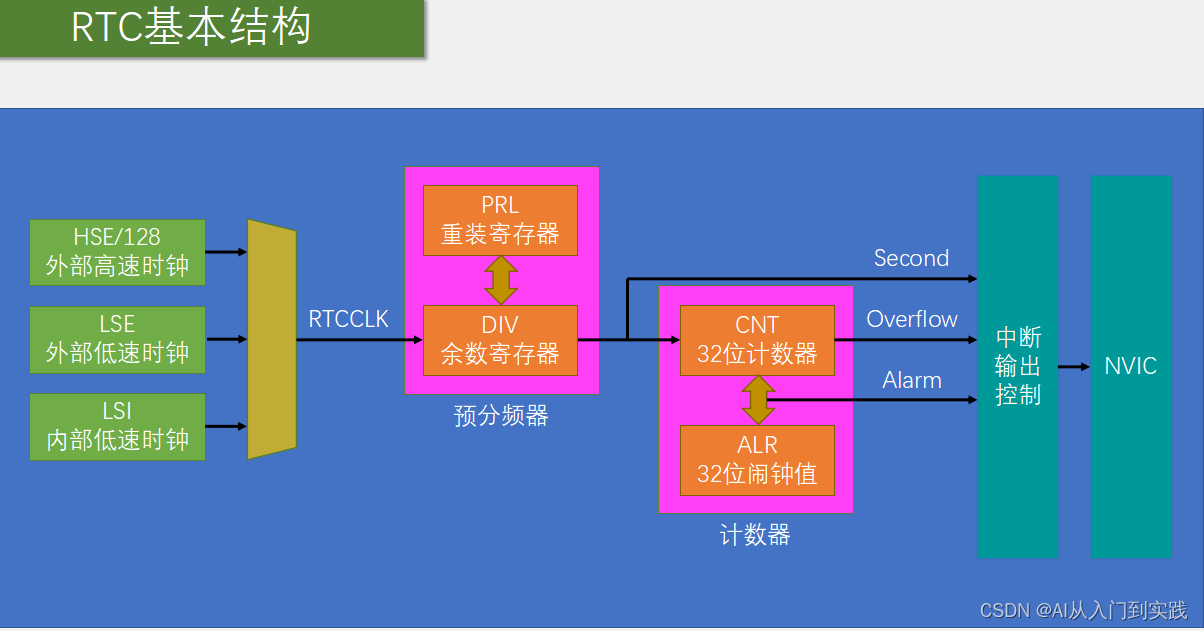
RTC操作注意事项

执行以下操作将使能对BKP和RTC的访问：
设置RCC_APB1ENR的PWREN和BKPEN，使能PWR和BKP时钟
设置PWR_CR的DBP，使能对BKP和RTC的访问
若在读取RTC寄存器时，RTC的APB1接口曾经处于禁止状态，则软件首先必须等待RTC_CRL寄存器中的RSF位（寄存器同步标志）被硬件置1
必须设置RTC_CRL寄存器中的CNF位，使RTC进入配置模式后，才能写入RTC_PRL、RTC_CNT、RTC_ALR寄存器
对RTC任何寄存器的写操作，都必须在前一次写操作结束后进行。可以通过查询RTC_CR寄存器中的RTOFF状态位，判断RTC寄存器是否处于更新中。仅当RTOFF状态位是1时，才可以写入RTC寄存器

相关文章：

【STM32】学习笔记-时间戳RTC

Unix时间戳 Unix 时间戳（Unix Timestamp）定义为从UTC/GMT的1970年1月1日0时0分0秒开始所经过的秒数，不考虑闰秒 时间戳存储在一个秒计数器中，秒计数器为32位/64位的整型变量 世界上所有时区的秒计数器相同，不同时区通…...

编程日记 2023/9/5 21:31:52

绿色能源迎来跨越式增长新时代

当今世界，百年未有之大变局加速演进，新一轮科技革命和产业变革深入发展，全球气候治理呈现新局面，新能源和信息技术紧密融合，生产生活方式加快转向低碳化、智能化，能源体系和发展模式正在进入非化石能源主导…...

编程日记 2023/9/5 21:30:51

【算法】函数渐近的界基础知识及定理

创作不易&#xff0c;本篇文章如果帮助到了你&#xff0c;还请点赞 关注支持一下♡>&#x16966;<)!! 主页专栏有更多知识&#xff0c;如有疑问欢迎大家指正讨论&#xff0c;共同进步&#xff01; &#x1f525;c系列专栏&#xff1a;C/C零基础到精通 &#x1f525; 给大…...

编程日记 2023/9/5 21:29:50

stable diffusion实践操作-writing

文章目录 前言一、优点1.1、免费开源1.2、拥有强大的外接模型 二、组成要素2.1 底模2.2 风格2.3 提示词2.4 参数配置 三、生图原理四、下载链接 实践正文一、安装1.1 电脑硬件配置查看1.2 安装本地版本的stable diffusion1.3 SD使用教程 二、模型介绍与下载2.1大模型2.2 Lora模…...

编程日记 2023/9/5 21:28:48

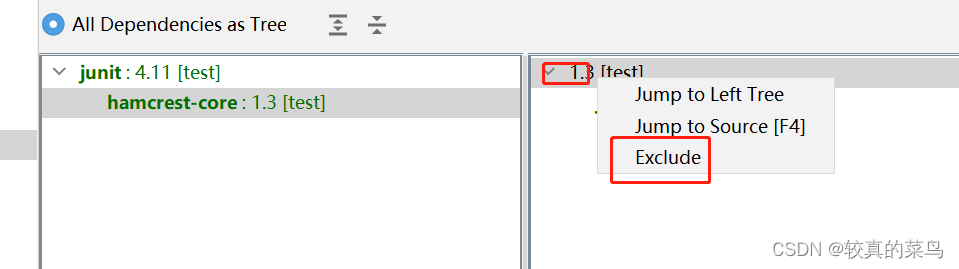
idea查找maven所有依赖

文章目录 idea自带的依赖结构图idea安装maven helper插件 idea自带的依赖结构图 缺点是只有依赖&#xff0c;没有版本 idea安装maven helper插件 settings–>plugins–>搜索maven helper并安装 安装后打开pom.xml文件会有依赖解析 勾选conflict就是有冲突的依赖选中…...

编程日记 2023/9/5 21:27:47

【业务功能篇97】微服务-springcloud-springboot-电商购物车模块-获取当前登录用户的购物车信息

购物车功能 一、购物车模块 1.创建cart服务 我们需要先创建一个cart的微服务&#xff0c;然后添加相关的依赖&#xff0c;设置配置&#xff0c;放开注解。 <dependencies><dependency><groupId>com.msb.mall</groupId><artifactId>mall-commo…...

编程日记 2023/9/5 21:26:46

Shell常用的几个正则表达式:[:alnum:], [:alpha:], [:upper:], [:lower:], [:digit:] 认知

一&#xff1a;通配符命令简介&#xff1a; 匹配符合相关条件的符号&#xff0c;匹配文件名查找。 通配符类型&#xff1a; *&#xff1a;匹配任意长度的任意字符 &#xff1f;&#xff1a;匹配任意单个字符 []&#xff1a;匹配指定范围内的任意单个字符 [^]&#xff1a;匹配指…...

编程日记 2023/9/5 21:25:45

简单的爬虫代码 爬（豆瓣电影）

路漫漫其修远兮&#xff0c;吾将上下而求索 这次写一个最简单的python爬虫代码&#xff0c;也是大多教程第一次爬取的&#xff0c;代码里面有个别的简单介绍&#xff0c;希望能加深您对python爬虫的理解。 本次爬取两个网页数据 一 爬取的网站 豆瓣电影 爬取网页中的&#…...

编程日记 2023/9/5 21:24:43

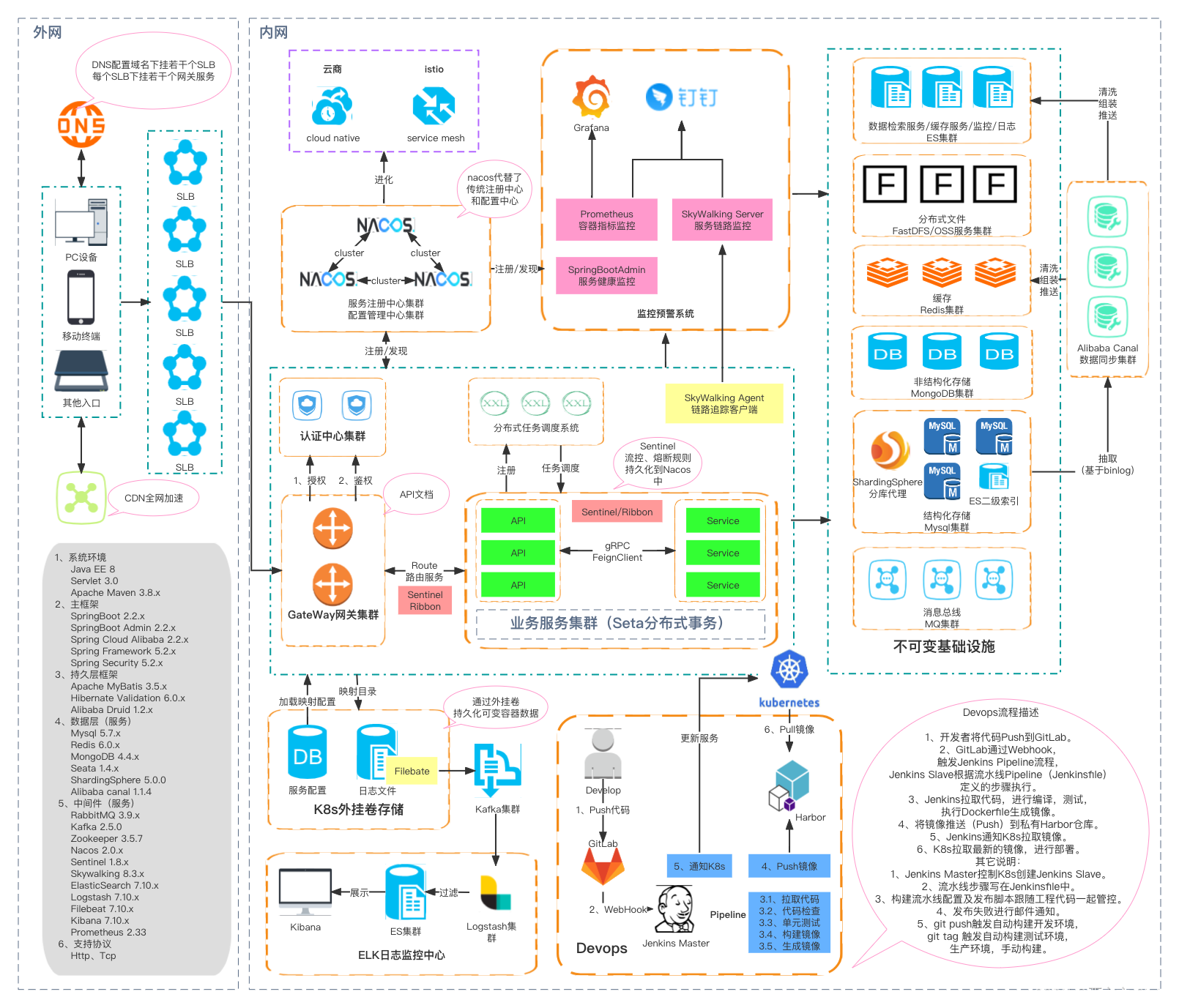
微服务之架构演变

随着互联网的发展&#xff0c;网站应用规模不断扩大&#xff0c;网站架构随之不断演变&#xff0c;演变历史大致分为单体应用架构-垂直应用架构-分布式架构-SOA架构-微服务架构-云原生架构 架构演变 单体应用架构 以前网站流量小&#xff0c;只需要一个应用就可以把所有功能…...

编程日记 2023/9/5 21:23:40

面试问题记录一 --- C++(Qt方向)

以下是我于2023年6~7月间换工作时遇到的面试题目，有需要的小伙伴可以参考下。约100个题目。 1 C和C++的区别 1) 文件区别：C源文件后缀 .c；C++源文件后缀 .cpp 2) 返回值： C默认返回int型；C++ 若无返回值，必须指定为void 3) 参数列表：C默认接收多个…...

编程日记 2023/9/5 21:22:39

使用词袋模型（BoW）测试提取图像的特征点和聚类中心

文章目录 环境配置代码测试 环境配置 (1) 导入opencv&#xff0c;参考链接 https://blog.csdn.net/Aer_7z/article/details/132612369(2) 安装numpy 激活虚拟环境的前提下&#xff0c;输入&#xff1a; pip install numpy(3) 安装sklearn 激活虚拟环境的前提下&#xff0c;输…...

编程日记 2023/9/5 21:21:37

利用vba处理Excel表格数据实现键值转化，适用于将编码转化成对应的文本

最近遇到了一个甲方需要提供系统登录的用户名单和对应的角色权限内容。无奈直接从数据库导出的数据对应的都是编码&#xff0c;没有转成中文&#xff0c;想着偷个懒能不能直接用Excel直接转&#xff0c;网上看了一下有修改单元格格式的&#xff0c;但需要编码是2到3个。多的就用…...

编程日记 2023/9/5 21:20:35

IntelliJ IDEA（Windows 版）的所有快捷键

&#x1fa81;&#x1f341; 希望本文能够给您带来一定的帮助&#x1f338;文章粗浅&#xff0c;敬请批评指正&#xff01;&#x1f341;&#x1f425; 大家好 本文参考了 IntelliJ IDEA 的官网&#xff0c;列举了IntelliJ IDEA&#xff08;Windows 版&#xff09;的所有快捷…...

编程日记 2023/9/5 21:19:34

文件上传漏洞全面渗透姿势

0x00 文件上传场景 (本文档只做技术交流) 文件上传的场景真的随处可见&#xff0c;不加防范小心&#xff0c;容易造成漏洞&#xff0c;造成信息泄露&#xff0c;甚至更为严重的灾难。 比如某博客网站评论编辑模块&#xff0c;右上角就有支持上传图片的功能&#xff0c;提交带…...

编程日记 2023/9/5 21:18:33

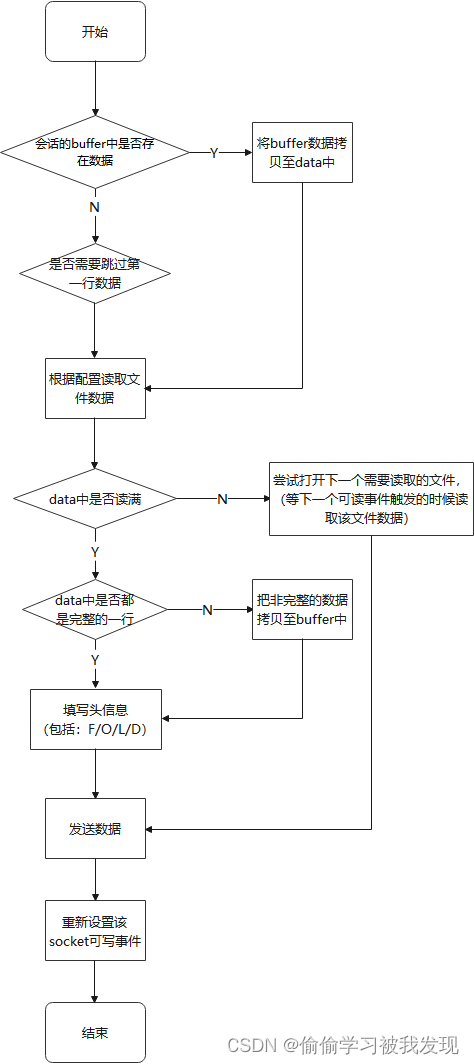
GreenPlum的gpfdist使用与原理流程分析

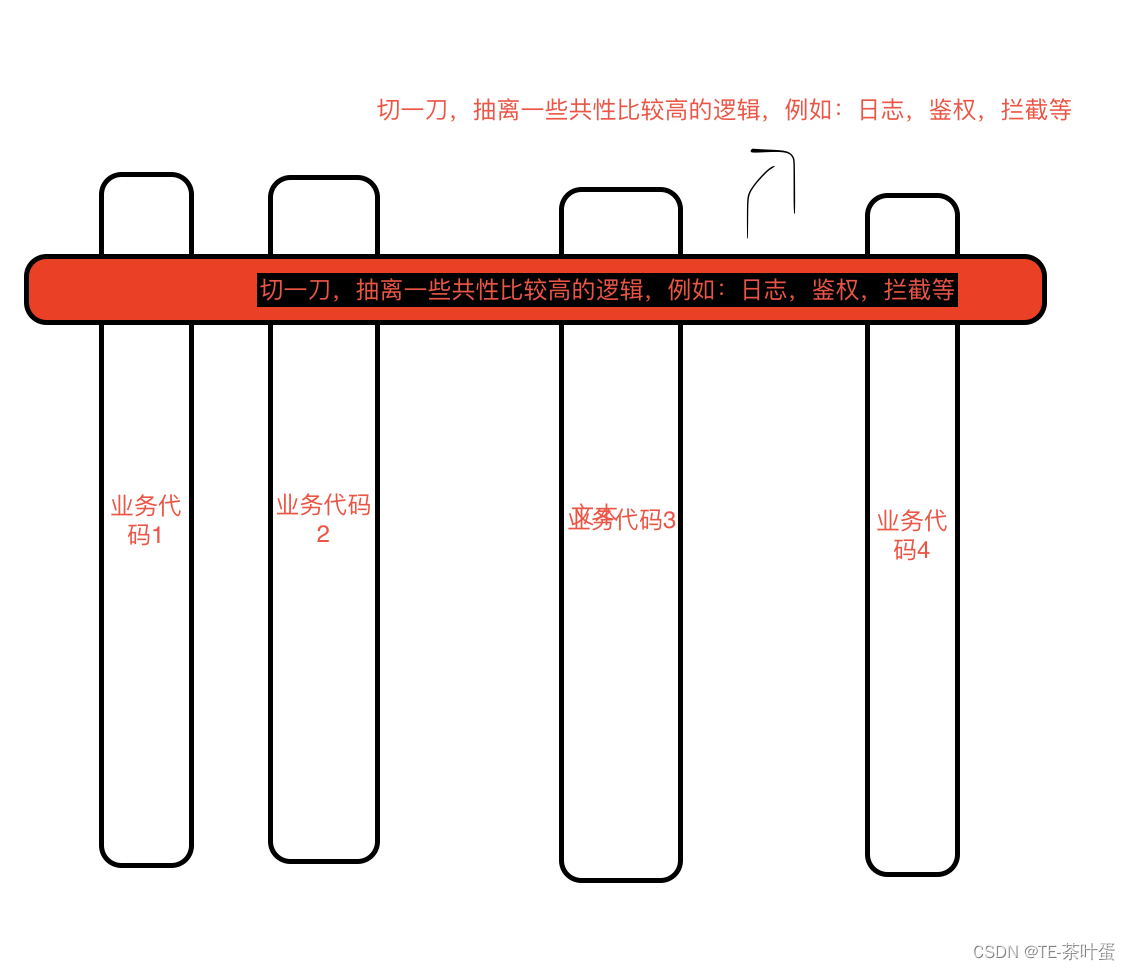
一、简介 GreenPlum 的数据导入功能作为对数据源的一种扩充&#xff0c;数据导入的方式有&#xff1a; 1、insert 该方式通过 sql 语句&#xff0c;把数据一条一条插入至表中。这种方式&#xff0c;不仅读取数据慢&#xff08;一条一条读取&#xff09;&#xff0c;且数据需要…...

编程日记 2023/9/5 21:17:32

Spring AOP与静态代理/动态代理

文章目录 一、代理模式静态代理动态代理代理模式与AOP 二、Spring AOPSping AOP用来处理什么场景jdk 动态代理cglib 动态代理面试题&#xff1a;讲讲Spring AOP的原理与执行流程 总结 一、代理模式 代理模式是一种结构型设计模式&#xff0c;它允许对象提供替代品或占位符&…...

编程日记 2023/9/5 21:16:28

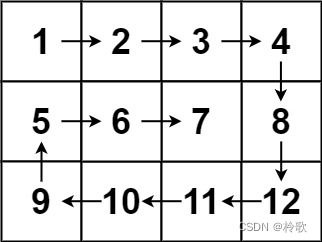
【LeetCode算法系列题解】第51~55题

CONTENTS LeetCode 51. N 皇后&#xff08;困难&#xff09;LeetCode 52. N 皇后 II&#xff08;困难&#xff09;LeetCode 53. 最大子序和&#xff08;中等&#xff09;LeetCode 54. 螺旋矩阵&#xff08;中等&#xff09;LeetCode 55. 跳跃游戏&#xff08;中等&#xff09; …...

编程日记 2023/9/5 21:15:26

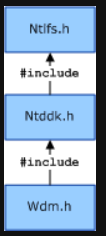
驱动开发错误汇编

本博文将会不定期更新。以便记录我的驱动开发生涯中的一些点点滴滴的技术细节和琐事。 1. link阶段找不到导出函数 比如"LNK2019 无法解析的外部符号 _FltCreateCommunicationPort32"。 出现这种情况的原因是&#xff0c;驱动的编译环境忽略了所有的默认库&#x…...

编程日记 2023/9/5 21:14:25

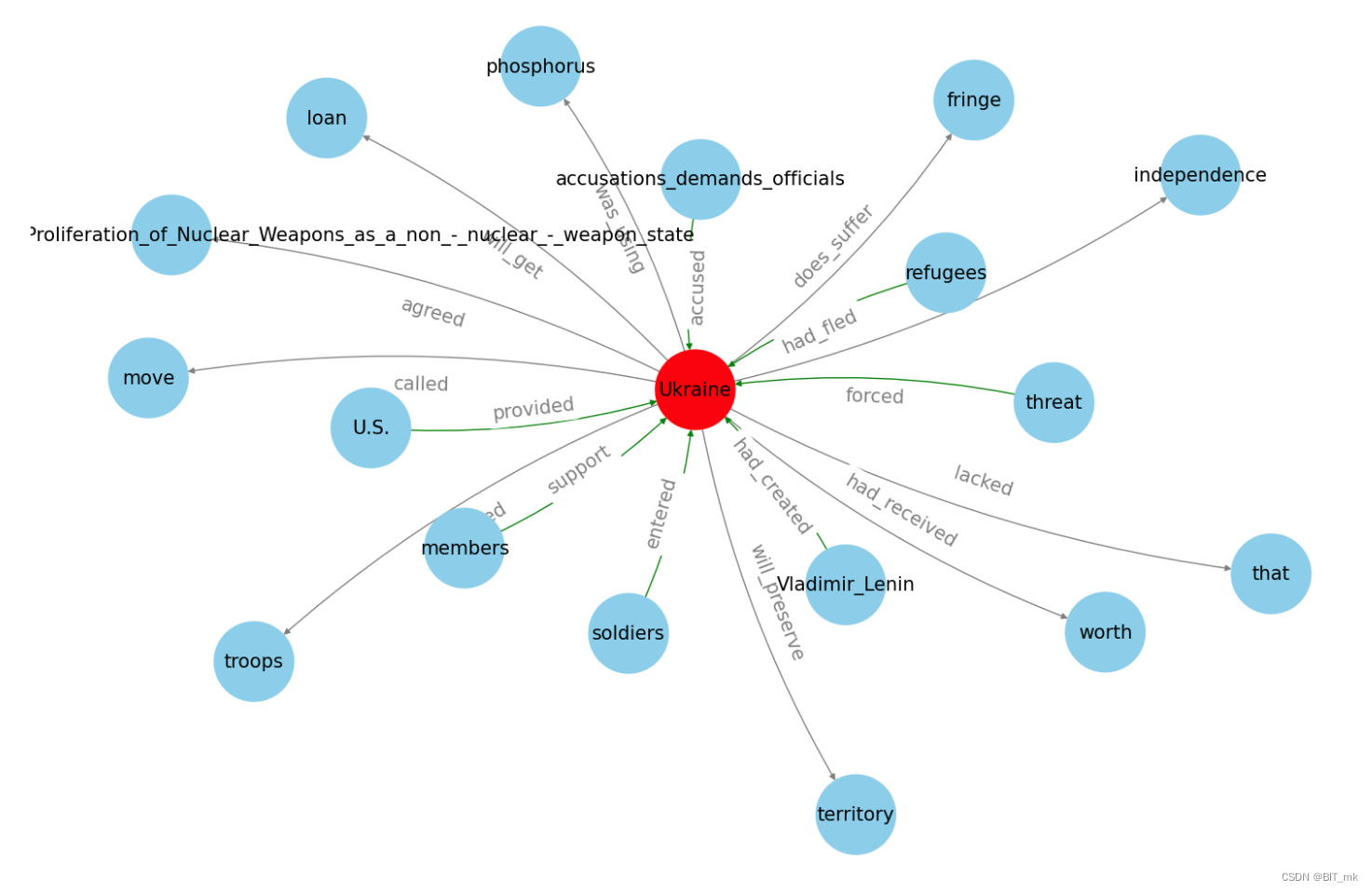
知识图谱项目实践

目录 步骤 SpaCy Textacy——Text Analysis for Cybersecurity Networkx Dateparser 导入库 写出页面的名称 ​编辑 自然语言处理 词性标注 可能标记的完整列表 依存句法分析&#xff08;Dependency Parsing&#xff0c;DEP&#xff09; 可能的标签完整列表 实例理…...

编程日记 2023/9/5 21:13:24

stable diffusion实践操作-提示词-人物属性

系列文章目录 stable diffusion实践操作-提示词 文章目录 系列文章目录前言一、提示词汇总1.1 人物属性11.2 人物属性2 前言 本文主要收纳总结了提示词-人物属性。 一、提示词汇总 1.1 人物属性1 角色类型人物身材胸部头发-发型头发-发色[女仆][霊烏路空][大腿][乳房][呆毛…...

编程日记 2023/9/5 21:12:23

8k长序列建模，蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂

蛋白质结合剂&#xff08;如抗体、抑制肽&#xff09;在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上&#xff0c;高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术&#xff0c;但这类方法普遍面临资源消耗巨大、研发周期冗长…...

编程新知 2026/1/25 13:18:12

Matlab | matlab常用命令总结

常用命令 一、 基础操作与环境二、 矩阵与数组操作（核心）三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结，涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

编程新知 2025/8/11 1:05:59

leetcodeSQL解题：3564. 季节性销售分析

leetcodeSQL解题&#xff1a;3564. 季节性销售分析 题目&#xff1a; 表&#xff1a;sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

编程新知 2026/2/10 3:44:54

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控，故障处理工具

第2章 虚拟机性能监控&#xff0c;故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令&#xff1a;jps [options] [hostid] 功能&#xff1a;本地虚拟机进程显示进程ID&#xff08;与ps相同&#xff09;&#xff0c;可同时显示主类&#x…...

编程新知 2026/1/15 1:34:10

学校时钟系统，标准考场时钟系统，AI亮相2025高考，赛思时钟系统为教育公平筑起“精准防线”

2025年#高考 将在近日拉开帷幕&#xff0c;#AI 监考一度冲上热搜。当AI深度融入高考&#xff0c;#时间同步 不再是辅助功能&#xff0c;而是决定AI监考系统成败的“生命线”。 AI亮相2025高考&#xff0c;40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕&#xff0c;江西、…...

编程新知 2026/2/8 22:07:52

JAVA后端开发——多租户

数据隔离是多租户系统中的核心概念&#xff0c;确保一个租户&#xff08;在这个系统中可能是一个公司或一个独立的客户&#xff09;的数据对其他租户是不可见的。在 RuoYi 框架&#xff08;您当前项目所使用的基础框架&#xff09;中&#xff0c;这通常是通过在数据表中增加一个…...

编程新知 2025/12/18 8:35:12

A2A JS SDK 完整教程：快速入门指南

目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库&#xff…...

编程新知 2025/12/12 8:42:24

解读《网络安全法》最新修订，把握网络安全新趋势

《网络安全法》自2017年施行以来&#xff0c;在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂&#xff0c;网络攻击、数据泄露等事件频发&#xff0c;现行法律已难以完全适应新的风险挑战。 2025年3月28日&#xff0c;国家网信办会同相关部门起草了《网络安全…...

编程新知 2026/1/31 4:40:38

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)

前言&#xff1a; 双亲委派机制对于面试这块来说非常重要&#xff0c;在实际开发中也是经常遇见需要打破双亲委派的需求&#xff0c;今天我们一起来探索一下什么是双亲委派机制&#xff0c;在此之前我们先介绍一下类的加载器。 目录 ​编辑 前言&#xff1a; 类加载器 1. …...

编程新知 2026/1/23 7:37:12

人工智能--安全大模型训练计划：基于Fine-tuning + LLM Agent

安全大模型训练计划&#xff1a;基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标&#xff1a;为安全大模型创建高质量、去偏、符合伦理的训练数据集&#xff0c;涵盖安全相关任务&#xff08;如有害内容检测、隐私保护、道德推理等&#xff09;。 1.1 数据收集 描…...

编程新知 2026/2/5 8:48:10