机器人中的数值优化(十三)——QP二次规划
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
二十、低维度严格凸的QP二次规划
1、低维度严格凸的QP二次规划数学描述
低维度严格凸二次规划,其数学描述如下式所示,其中 M Q M_Q MQ是严格正定的对称矩阵,目标函数是严格凸函数,维度n是低维的
min x ∈ R n 1 2 x T M Q x + c Q T x , s.t. A Q x ≤ b Q \operatorname*{min}_{x\in\mathbb{R}^{n}}\frac{1}{2}x^{\mathrm{T}}M_{\mathcal{Q}}x+c_{\mathcal{Q}}^{\mathrm{T}}x\text{, s.t. }A_{\mathcal{Q}}x\leq b_{\mathcal{Q}} x∈Rnmin21xTMQx+cQTx, s.t. AQx≤bQ
M Q M_Q MQ是严格正定的,因此可以对其进行Cholesky分解,Cholesky 分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。它要求矩阵的所有特征值必须大于零,故分解的下三角的对角元也是大于零的。
M Q = L Q L Q T M_{\cal Q}=L_{\cal Q}L_{\cal Q}^{\mathrm{T}} MQ=LQLQT
这个QP问题等价于关于y的最小二范数问题:
y = L Q T x + L Q − 1 c Q o r x = L Q − T y − ( L Q L Q T ) − 1 c Q y=L_{\cal Q}^{\mathrm T}x+L_{\cal Q}^{-1}c_{\cal Q}\quad\mathrm{or}\quad x=L_{\cal Q}^{-\mathrm T}y-\left(L_{\cal Q}L_{\cal Q}^{\mathrm T}\right)^{-1}c_{\cal Q} y=LQTx+LQ−1cQorx=LQ−Ty−(LQLQT)−1cQ
我们可以把上面x关于y的表达式代入到目标函数中,整理后得到等价的表达式如下所示:
min y ∈ R n 1 2 y T y , s . t . E y ≤ f \min_{y\in\mathbb{R}^n}\frac12y^\mathrm{T}y,\mathrm{~s.t.~}Ey\leq f y∈Rnmin21yTy, s.t. Ey≤f
其中 E = A Q L Q − T , f = A Q ( L Q L Q T ) − 1 c Q + b Q E=A_{\mathcal{Q}}L_{\mathcal{Q}}^{-\mathrm{T}},f=A_{\mathcal{Q}}\big(L_{\mathcal{Q}}L_{\mathcal{Q}}^{\mathrm{T}}\big)^{-1}c_{\mathcal{Q}}+b_{\mathcal{Q}} E=AQLQ−T,f=AQ(LQLQT)−1cQ+bQ
对上述表达式求解得到最优的y后(在多面体中找一个范数最小的点,也即离原点最近的点),再将得到的y代入到上面x关于y的表达式,即可得到最优的x。
线性不等式约束 E y ≤ f Ey\leq f Ey≤f构成了如下图所示的可行域,在该可行域内找一个使得下式最小的解,即y的二范数的平方的最小的解,也就是可行域中离原点最近的点。
min y ∈ R n 1 2 y T y = 1 2 ∣ ∣ y ∣ ∣ 2 2 \min_{y\in\mathbb{R}^n}\frac12y^\mathrm{T}y=\frac12{||y||_2}^2 y∈Rnmin21yTy=21∣∣y∣∣22

2、一维的QP二次规划
与之前介绍的LP线性规划类似,一维情况下的数学描述及可行域的计算如下图所示,所不同的是,确定了可行域后,QP更容易得到最优解,只需要找到可行域中距离原点最近的点即可,若原点位于可行域左侧,则可行域左端点即为最优解,同理,若原点位于可行域右侧,则可行域右端点即为最优解,若原点位于可行域内部,则原点即为最优解。

3、二维的QP二次规划
与之前介绍的LP线性规划类似,二维情况下的解决思路依然是,在加入新的约束后,若之前的最优解依然在可行域中,则最优解不变,若之前的最优解已经不在可行域中了,则需要将之前的约束边界投影到当前新加入的约束边界上,转化得到一维的可行域,再在这个一维的可行域上寻找新的最优解,与LP不同的是,得到一维的可行域后,只需要将原点也投影到新加入的约束边界上,然后找到一维可行域中与原点的投影点距离最近的点即可


4、更一般的d维QP二次规划
与前文介绍的d维的LP线性规划的主要思想类似,d维的二次规划在当前最优解不满足新加入的约束时,也将其转换成d-1维的二次规划,这跟上面2维二次规划时转换成1维二次规划的思想是相同的,这种思想有点像递归的思想。

上图中给出的伪代码中,输入参数H即不等式约束 a T y < = b a^\mathrm{T}y<=b aTy<=b,也即一系列半空间,如果此时H的维度是一维的,则直接采用上文中介绍的一维情况的解决方法求解,若此时c不是一维的,则初始化一个空集 I I I,可以提前用Fisher-Yates算法对H的序列进行打乱,打乱后进行for循环时,每次依次从H中取一个h,然后判断:
情况1:若当前最优解属于h,则当前最优解满足约束h,不需要计算新的最优解,直接将h添加到集合 I I I中,继续进行下一轮for循环,处理下一个约束h
情况2:若当前的最优解不属于h,则需要计算一个新的最优解x,将已经加入到集合 I I I中的约束投影到约束h的边界上,得到低一个维度的H’,将原点也投影到h上,得到低一个维度的原点v,M是h的一个正交基,然后将低一个维度的H’作为参数递归调用LowDimMinNorm()函数本身进行降维处理,直至降为1维情况。然后就可以得到新的y’,运用关系式 y ← M y ′ + v y\leftarrow My^{\prime}+v y←My′+v得到新的最优解y,此时约束h已经满足,将其添加到集合 I I I中,本轮循环结束,继续进行下一轮for循环,处理下一个约束h。
for循环结束后,即可得到满足所有约束hi的最优解y,然后再带入到x关于y的表达式,得到满足所有约束的最优解x。

在前文介绍的LP线性规划中,把d维的问题转换成d-1维的问题,并逐步转换为1维问题是通过高斯消元法完成的,接下来介绍在QP二次规划中,如何把高维问题转换成低维问题。
在上图中的例子中,之前的约束构成的空间如绿色区域所示,新加入的约束h如图中灰色区域所示,新的最优解 y ∗ y^* y∗必然位于约束h所确定的平面上且位于之前的约束构成的区域的内部,原点o在约束h所确定的平面上的投影点为v,由勾股定理可得他们满足以下表达式
∥ y ∗ − o ∥ 2 = ∥ y ∗ − v ∥ 2 + ∥ v − o ∥ 2 \|y^*-o\|^2= \|y^*-v\|^2+\|v-o\|^2 ∥y∗−o∥2=∥y∗−v∥2+∥v−o∥2
假设,我们已知约束h所确定的平面中以v为原点的一组标准正交基M,然后,约束h所确定的灰色平面中所有点均可表示为该组标准正交基的坐标,因此 y ∗ y^* y∗满足如下表达式,其中 y 1 ′ y_1^{\prime} y1′和 y 2 ′ y_2^{\prime} y2′是 y ∗ − v y^*-v y∗−v在标准正交基下的坐标:
y ∗ − v = y 1 ′ M 1 + y 2 ′ M 2 = M y ′ y^*-v=y_1^{\prime}M_1+y_2^{\prime}M_2=My^{\prime} y∗−v=y1′M1+y2′M2=My′
将上式代入到 ∥ y ∗ − o ∥ 2 = ∥ y ∗ − v ∥ 2 + ∥ v − o ∥ 2 \|y^*-o\|^2= \|y^*-v\|^2+\|v-o\|^2 ∥y∗−o∥2=∥y∗−v∥2+∥v−o∥2中可得以下表达式(因为M是标准正交基,所以 M T M = I M^TM=I MTM=I所以求范数后可以约去 )
∥ M y ′ ∥ 2 + ∥ v − o ∥ 2 = ∥ y ′ ∥ 2 + ∥ v − o ∥ 2 = ∥ y ∗ ∥ 2 \|My'\|^2+\|v-o\|^2=\|y'\|^2+\|v-o\|^2=\|y^*\|^2 ∥My′∥2+∥v−o∥2=∥y′∥2+∥v−o∥2=∥y∗∥2
因为,v-o是常量,所以求最小的y*可以转换为求最小的y’,把一个线性等式约束上的最小范数问题转化为一个无约束的最小范数问题。
接下来看一下,上面提到的点v和标准正交基M如何求,约束h= g T y = f g^Ty=f gTy=f,可知当 y = f g g T g y=\frac{\color{red}{fg}}{\color{red}{g^Tg}} y=gTgfg必然满足该约束,所以v可取为: v = f g g T g v=\frac{\color{red}{fg}}{\color{red}{g^Tg}} v=gTgfg

g是h约束所确定平面的法向量,那么平面的标准正交基均垂直于g,我们可以先构造下图中绿色的这样一组正交基,其某一个维度的模长为||g||,然后再通过旋转把模长为||g||的那个基变得跟g同方向,其他的绿色基,自然也就变成了我们想要的图中黄色的基M。其相关数学表达式如下所示:
u = g − ∥ g ∥ e i u=g-\|g\|e_i u=g−∥g∥ei
H = I d − 2 u u T u T u H=I_d-\frac{2uu^\mathrm{T}}{u^\mathrm{T}u} H=Id−uTu2uuT
先根据g和ei计算出u,再代入上式计算出H(注意这里的H不是约束的意思),然后把H转置一下,得到 H T H^T HT后去掉第i列,就得到我们想要的M了,M中的d-1个列向量是由H中的d-1个行向量构成的

参考资料:
1、数值最优化方法(高立 编著)
2、机器人中的数值优化
相关文章:

机器人中的数值优化(十三)——QP二次规划
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...
语言深入理解指针(非常详细)(三)
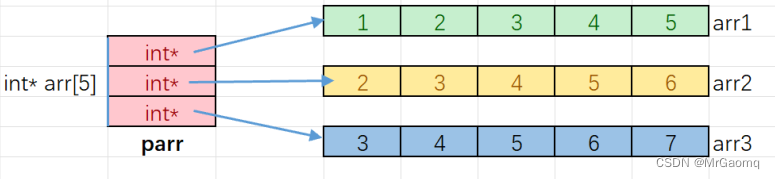
目录 数组名的理解使用指针访问数组 一维数组传参的本质二级指针指针数组指针数组模拟二维数组 数组名的理解 在上⼀个章节我们在使用指针访问数组的内容时,有这样的代码: int arr[10] {1,2,3,4,5,6,7,8,9,10}; int *p &arr[0];这里我们使用 &am…...

实训笔记8.31
实训笔记8.31 8.31笔记一、项目开发流程一共分为七个阶段1.1 数据产生阶段1.2 数据采集存储阶段1.3 数据清洗预处理阶段1.4 数据统计分析阶段1.5 数据迁移导出阶段1.6 数据可视化阶段 二、项目数据清洗预处理的实现2.1 清洗预处理规则2.1.1 数据清洗规则2.1.2 数据预处理规则 2…...

el-table 垂直表头
效果如下: 代码如下: <template><div class"vertical_head"><el-table style"width: 100%" :data"getTblData" :show-header"false"><el-table-columnv-for"(item, index) in getHe…...

B081-Lucene+ElasticSearch
目录 认识全文检索概念lucene原理全文检索的特点常见的全文检索方案 Lucene创建索引导包分析图代码 搜索索引分析图代码 ElasticSearch认识ElasticSearchES与Kibana的安装及使用说明ES相关概念理解和简单增删改查ES查询DSL查询DSL过滤 分词器IK分词器安装测试分词器 文档映射(字…...

机器学习:塑造未来的核心力量
着科技的飞速发展,机器学习已经成为我们生活中不可或缺的一部分。无论是搜索引擎、推荐系统,还是自动驾驶汽车和机器人,都依赖于机器学习算法。本文将探讨机器学习的基本概念、应用领域以及未来发展趋势。 一、机器学习的基本概念 机器学习…...
RK3568-i2c-适配8010rtc时钟芯片
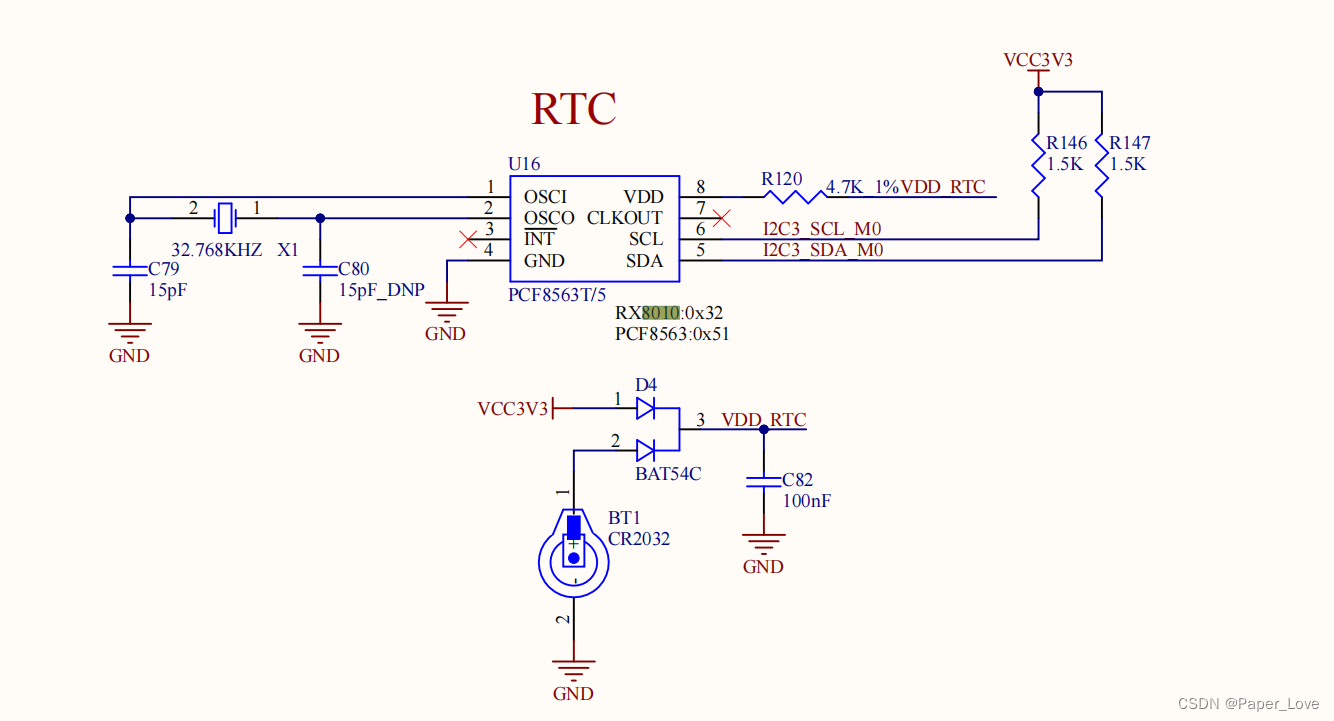
硬件连接 从硬件原理图中可以看出,rtc时钟芯片挂载在i2c3总线上,设备地址需要查看芯片数据手册。编写设备树 &i2c3 {status "okay";rx8010: rx801032 {compatible "epson,rx8010";reg <0x32>;}; };使能驱动 /kernel/…...

Spring Security - 基于内存快速demo
基于内存方式 - 只作学习参考1.引入依赖<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-thymeleaf</artifactId></dependency>2.login.html、index.html、fail.htmllogin.html:<form method…...

6 | 从文本文件中读取单词并输出不重复的单词列表
Transformation 操作 Transformation 操作是用于从一个 RDD(Resilient Distributed Dataset)创建一个新的 RDD,通常是通过对原始 RDD 的元素进行映射、筛选、分组等操作来实现的。Transformation 操作不会立即执行,而是惰性计算,只有在 Action 操作触发时才会真正执行。以…...
配置)
【微信小程序篇】- 多环境(版本)配置
最近自己在尝试使用AIGC写一个小程序,页面、样式、包括交互函数AIGC都能够帮我完成(不过这里有一点问题AIGC的上下文关联性还是有限制,会经常出现对于需求理解跑偏情况,需要不断的重复强调,并纠正错误,才能得到你想要的…...
)
ssh配置(一、GitLabGitHub)
一. 为什么配置ssh 使用 ssh 克隆项目,更加安全方便。 git clone 项目时一般使用两种协议 https 和 ssh 。 二. 原理的通俗解释 ssh 解决的问题是登录时的用户身份验证问题,默认使用 RSA(也支持其他算法: RSA、DSA、ECDSA、EdD…...
开了抖店后就可以直播带货了吗?想在抖音带货的,建议认真看完!
我是王路飞。 关于抖店和直播带货的关系,其实很多人经常搞不清楚。 不然的话,也不会有这个问题的出现了:开了抖店后就可以直播带货了吗? 在我看来,这个问题很简单,但在不了解抖音电商和直播带货其中门道…...
【深度学习实验】数据可视化
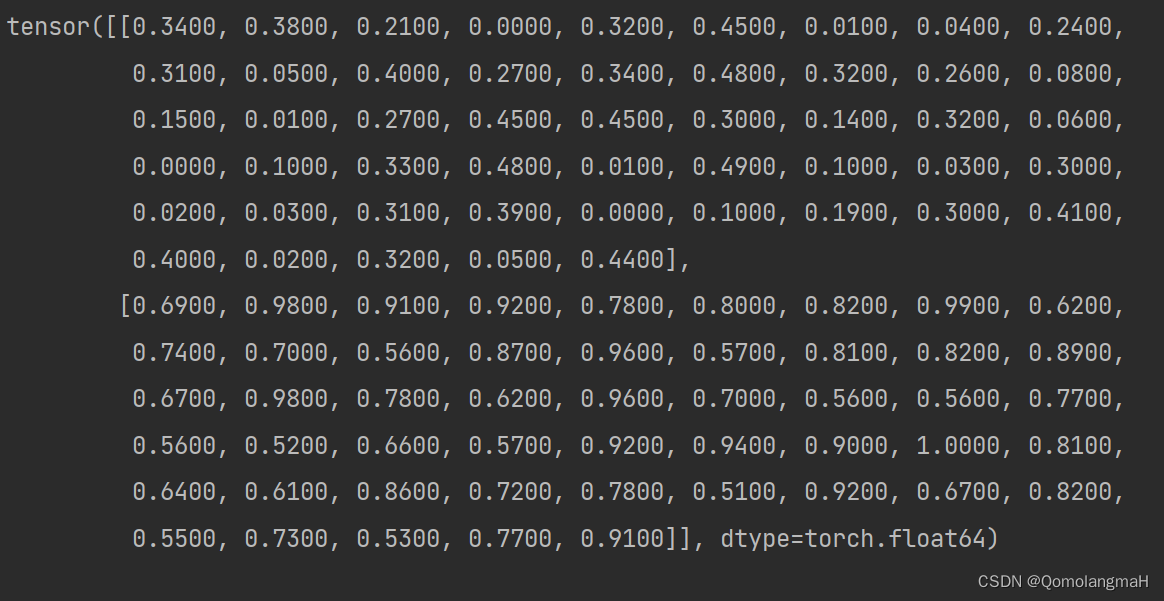
目录 一、实验介绍 二、实验环境 三、实验内容 0. 导入库 1. 归一化处理 归一化 实验内容 2. 绘制归一化数据折线图 报错 解决 3. 计算移动平均值SMA 移动平均值 实验内容 4. 绘制移动平均值折线图 5 .同时绘制两图 6. array转换为tensor张量 7. 打印张量 一、…...

【Golang】函数篇
1、golang函数基本定义与使用 func 函数名 (形参列表) (返回值类型列表) {函数体return 返回值列表 }其中func用于表明这是一个函数,剩下的东西与其他语言的函数基本一致,在定义与使用的时候注意函数名、参数、返回值书写的位置即可。下面使用一个例子…...
在ubuntu上安装ns2和nam(ubuntu16.04)
在ubuntu上安装ns2和nam 版本选择安装ns2安装nam 版本选择 首先,版本的合理选择可以让我们避免很多麻烦 经过测试,ubuntu的版本选择为ubuntu16.04,ns2的版本选择为ns-2.35,nam包含于ns2 资源链接(百度网盘) 链接:https://pan.bai…...

SpringCloudAlibaba之Sentinel介绍
文章目录 1 Sentinel1.1 Sentinel简介1.2 核心概念1.2.1 资源1.2.2 规则 1.3 入门Demo1.3.1 引入依赖1.3.2 集成Spring1.3.3 Spring中资源规则 1.4 Sentinel控制台1.5 核心原理1.5.1 NodeSelectorSlot1.5.2 ClusterBuilderSlot1.5.3 LogSlot1.5.4 StatisticSlot1.5.5 Authority…...
苹果微信聊天记录删除了怎么恢复?果粉原来是这样恢复的
粗心大意删除了微信聊天记录?有时候,一些小伙伴可能只是想要删除一部分聊天记录,但是在进行批量删除时,不小心勾选到了很重要的对话,从而导致记录丢失。 如果这时想找回聊天记录该怎么办?微信聊天记录删除…...
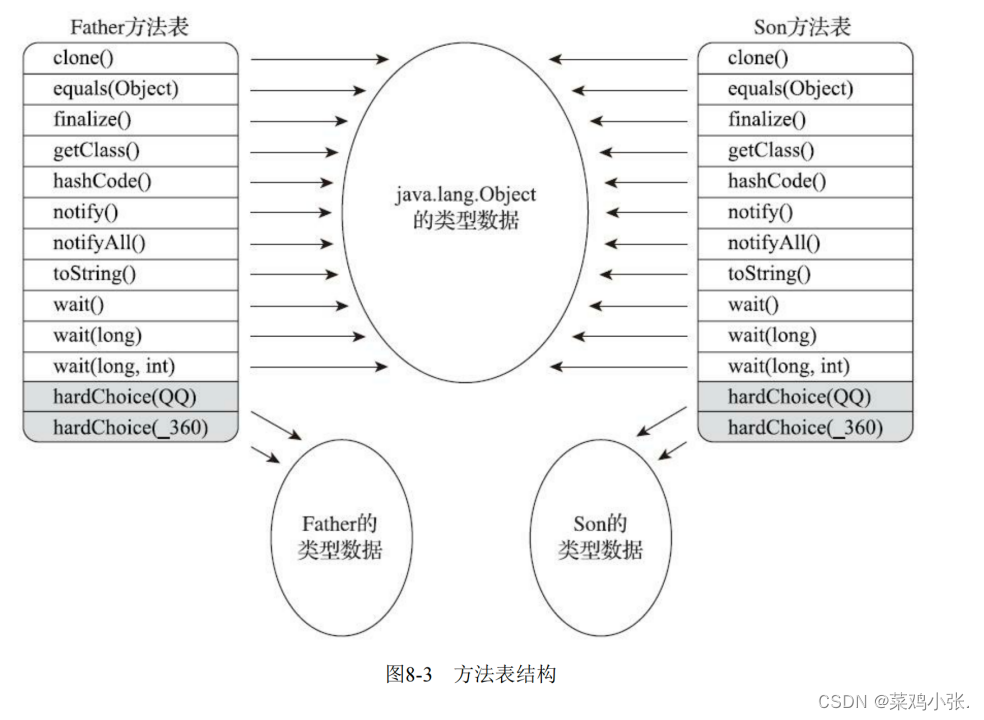
JVM的故事——虚拟机字节码执行引擎
虚拟机字节码执行引擎 文章目录 虚拟机字节码执行引擎一、概述二、运行时栈帧结构三、方法调用 一、概述 执行引擎Java虚拟机的核心组成之一,它是由软件自行实现的,能够执行那些不被硬件直接支持的指令集格式。 对于不同的虚拟机实现,执行引…...
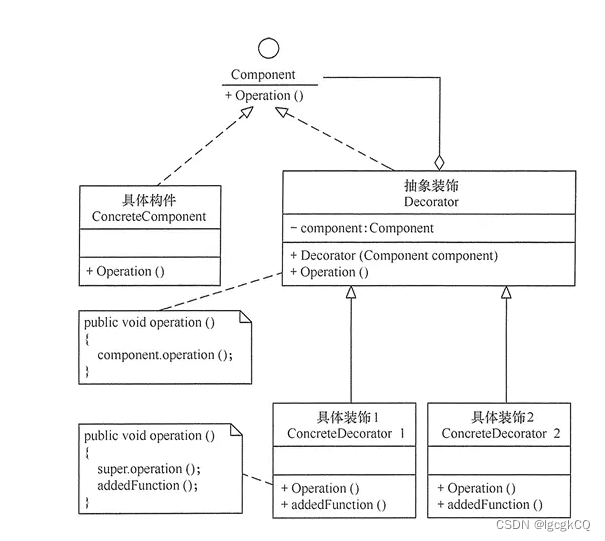
设计模式之适配器与装饰器
目录 适配器模式 简介 角色 使用 优缺点 使用场景 装饰器模式 简介 优缺点 模式结构 使用 使用场景 适配器模式 简介 允许将不兼容的对象包装成一个适配器类,使得其他类可以通过适配器类与原始对象进行交互,从而提高兼容性 角色 目标角色…...
服务器数据恢复- Ext4文件系统分区挂载报错的数据恢复案例
Ext4文件系统相关概念: 块组:Ext4文件系统的空间被划分为若干个块组,每个块组内的结构大致相同。 块组描述符表:每个块组都对应一个块组描述符,这些块组描述符统一放在文件系统的前部,称为块组描述符表。每…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
