当前位置： 首页 > news >正文

开了抖店后就可以直播带货了吗？想在抖音带货的，建议认真看完！

news 文章来源：https://blog.csdn.net/RL1055/article/details/132692864 2025/5/14 23:08:09

我是王路飞。

关于抖店和直播带货的关系，其实很多人经常搞不清楚。

不然的话，也不会有这个问题的出现了：开了抖店后就可以直播带货了吗？

在我看来，这个问题很简单，但在不了解抖音电商和直播带货其中门道的人来说，确实有些难以理解。

所以今天给你们分享的内容，主要就是帮助你们理清楚思路，让你们知道什么是抖店，以及什么是直播带货，想在抖音带货的，建议认真看完！

先说直播带货吧，可能大部分人抖音的这个变现方式比较感兴趣，毕竟太火了。

首先呢，你要想在抖音做直播带货的的话，有几个前提条件：抖音账号+抖音粉丝+短视频拍摄+直播带货的能力。

注意，这几个条件，缺一不可，缺少一个环节，你就没办法做到在抖音直播带货。

你在抖音直播带货的前提，一定是你在抖音有大量的粉丝能让你转化变现的，否则你把产品卖给谁呢？

而在抖音积累粉丝的前提，就是先通过拍摄短视频去吸引别人关注你，并且你还要有能力把粉丝长久留存住，才能为之后开直播带货做准备。

所以你就要问自己几个问题了：我在抖音有粉丝吗？我能否面对直播镜头不紧张？我是否有拍短视频和运营账号的能力，先想清楚这几个问题，才能去考虑开直播带货。

再说下抖店吧，它与直播带货不一样，直播带货依赖的是账号和粉丝，也就是抖音橱窗，而橱窗也只是抖音的一个电商功能罢了。

但是抖店属于抖音一个独立的店铺，有自己独立的后台和独立的app存在。

你不需要做账号，也不需要有粉丝，0粉丝就可以在抖音开店，甚至也不需要你有货源，抖店是可以做无货源模式的。

可以说，抖店就是抖音专门为了普通人设立的卖货渠道，尤其是那些在抖音没有粉丝优势、没有颜值优势、没有才艺优势的普通人。

在身份上，开店后你属于抖音上的商家，但是做直播带货的话，你就是达人了。

所以，并不是说，开通抖店后，你就可以直播带货了，它们根本就是两码事。

还要额外提醒你们一句，不要妄想两手抓，你能把一件事给做好已经很不容易了，不要贪多，时间/精力都不允许的。

尤其是在抖音没有优势的普通人，我给你们的建议是在抖音开店要好过在抖音直播带货。

现在能在抖音直播并且带货的达人，都是之前趁着抖音风口起来的，已经完成了账号、渠道、团队等等积累和搭建，你这时候还妄想通过抖音短视频再去开直播的话，不能说一点希望都没有，只能说运气要大于一切。

但是做抖店的话，跟运气就没什么关系了，你能沉下心，弯下腰去做事，你就可以拿到结果，这是可以给你保证的。

如果你想更进一步了解抖店的内容，可以先关注，然后私信我，给你发一个项目介绍和资料包（免费的）

想了解更多关于抖音小店的细节、规则、内容、玩法等，也可以

公众号，电商王路飞（可领取项目介绍）

相关文章：

开了抖店后就可以直播带货了吗？想在抖音带货的，建议认真看完！

我是王路飞。 关于抖店和直播带货的关系，其实很多人经常搞不清楚。 不然的话，也不会有这个问题的出现了：开了抖店后就可以直播带货了吗？ 在我看来，这个问题很简单，但在不了解抖音电商和直播带货其中门道…...

编程日记 2023/9/5 23:58:02

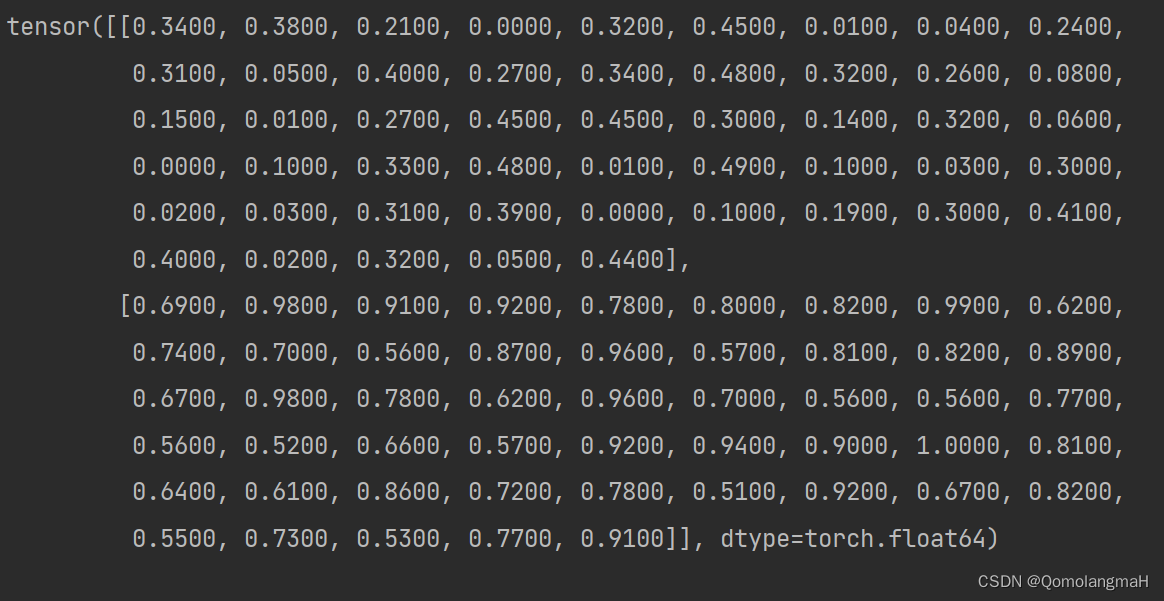
【深度学习实验】数据可视化

目录 一、实验介绍 二、实验环境 三、实验内容 0. 导入库 1. 归一化处理 归一化 实验内容 2. 绘制归一化数据折线图 报错 解决 3. 计算移动平均值SMA 移动平均值 实验内容 4. 绘制移动平均值折线图 5 .同时绘制两图 6. array转换为tensor张量 7. 打印张量 一、…...

编程日记 2023/9/5 23:57:01

【Golang】函数篇

1、golang函数基本定义与使用 func 函数名 (形参列表) (返回值类型列表) {函数体return 返回值列表 }其中func用于表明这是一个函数，剩下的东西与其他语言的函数基本一致，在定义与使用的时候注意函数名、参数、返回值书写的位置即可。下面使用一个例子…...

编程日记 2023/9/5 23:56:00

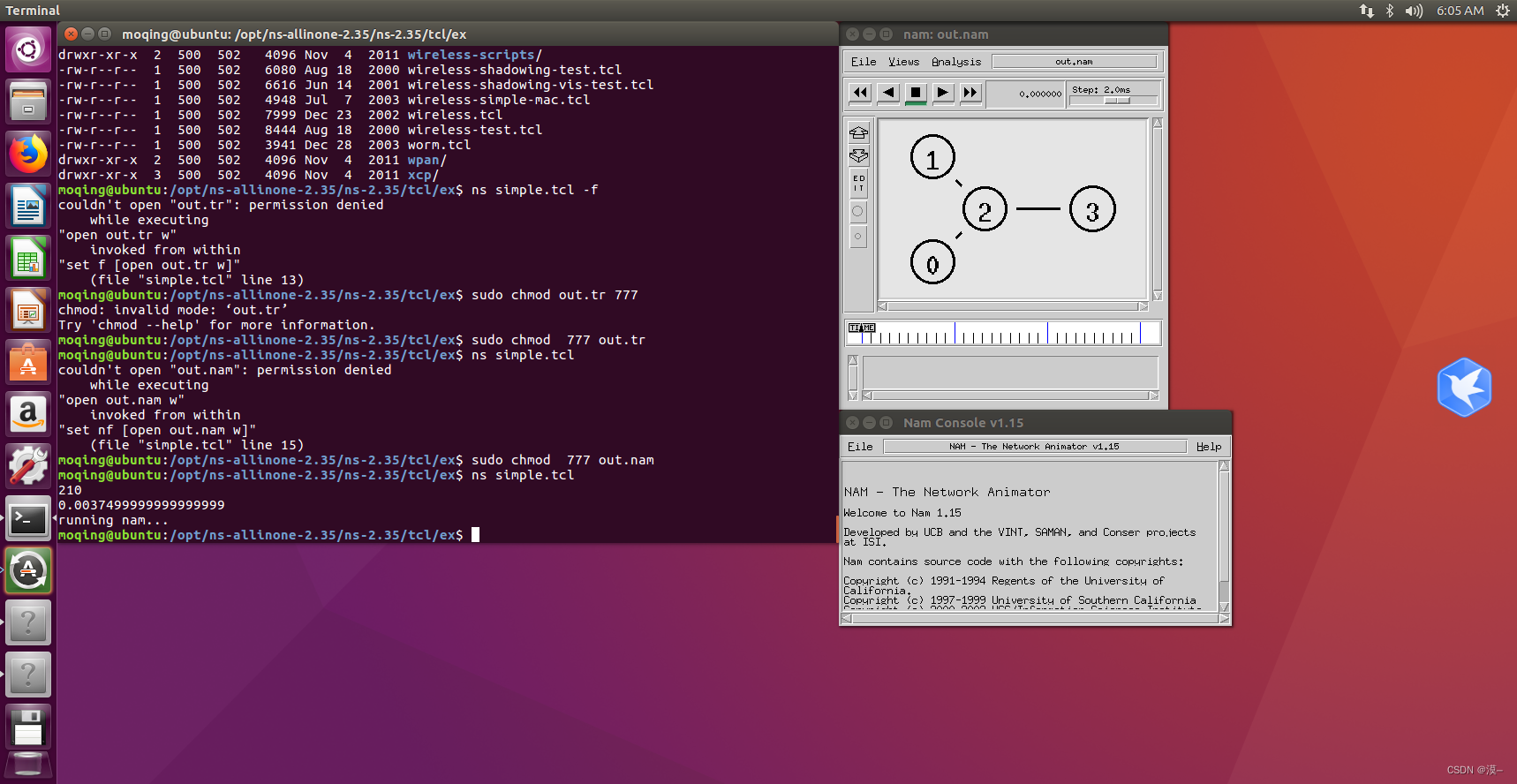
在ubuntu上安装ns2和nam(ubuntu16.04)

在ubuntu上安装ns2和nam 版本选择安装ns2安装nam 版本选择 首先，版本的合理选择可以让我们避免很多麻烦 经过测试，ubuntu的版本选择为ubuntu16.04，ns2的版本选择为ns-2.35，nam包含于ns2 资源链接(百度网盘) 链接:https://pan.bai…...

编程日记 2023/9/5 23:54:58

SpringCloudAlibaba之Sentinel介绍

文章目录 1 Sentinel1.1 Sentinel简介1.2 核心概念1.2.1 资源1.2.2 规则 1.3 入门Demo1.3.1 引入依赖1.3.2 集成Spring1.3.3 Spring中资源规则 1.4 Sentinel控制台1.5 核心原理1.5.1 NodeSelectorSlot1.5.2 ClusterBuilderSlot1.5.3 LogSlot1.5.4 StatisticSlot1.5.5 Authority…...

编程日记 2023/9/5 23:53:57

苹果微信聊天记录删除了怎么恢复？果粉原来是这样恢复的

粗心大意删除了微信聊天记录？有时候，一些小伙伴可能只是想要删除一部分聊天记录，但是在进行批量删除时，不小心勾选到了很重要的对话，从而导致记录丢失。 如果这时想找回聊天记录该怎么办？微信聊天记录删除…...

编程日记 2023/9/5 23:52:56

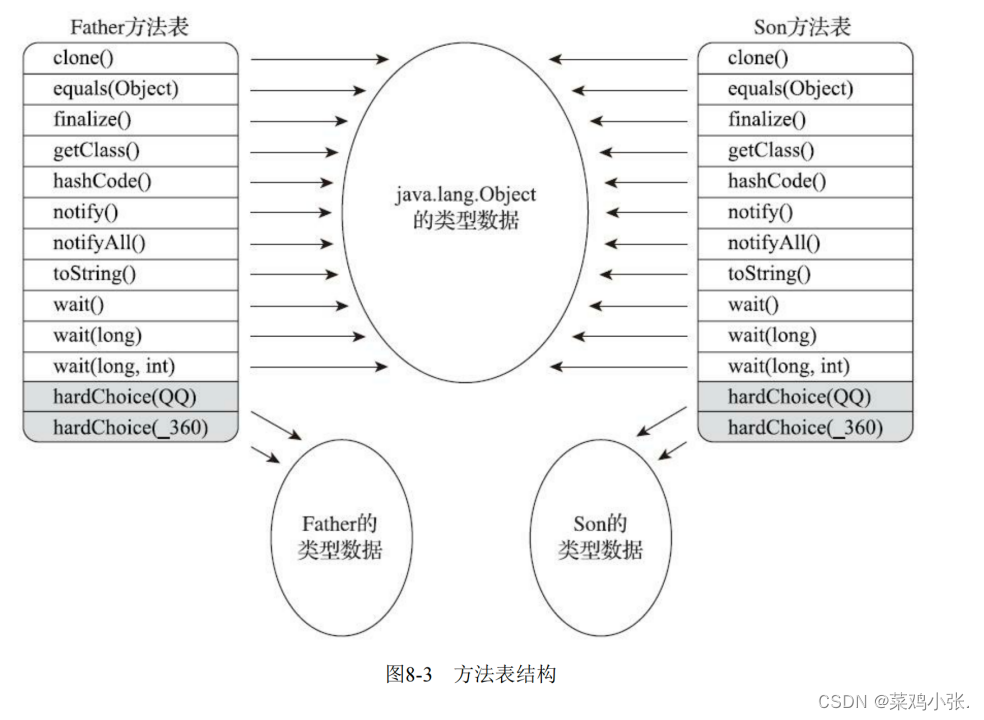
JVM的故事——虚拟机字节码执行引擎

虚拟机字节码执行引擎 文章目录 虚拟机字节码执行引擎一、概述二、运行时栈帧结构三、方法调用 一、概述 执行引擎Java虚拟机的核心组成之一，它是由软件自行实现的，能够执行那些不被硬件直接支持的指令集格式。 对于不同的虚拟机实现，执行引…...

编程日记 2023/9/5 23:51:55

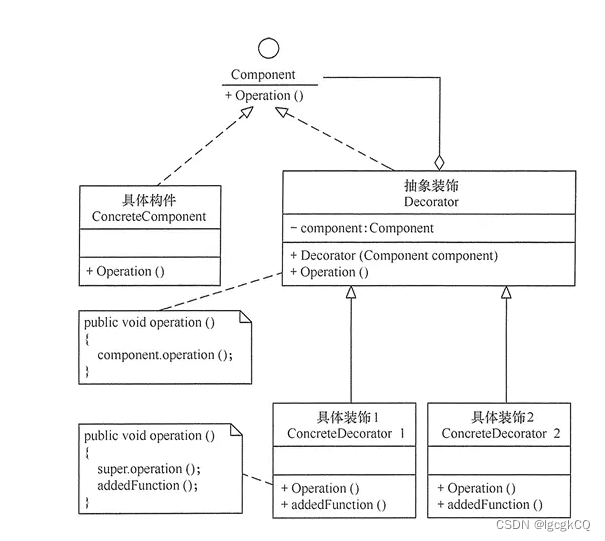
设计模式之适配器与装饰器

目录 适配器模式 简介 角色 使用 优缺点 使用场景 装饰器模式 简介 优缺点 模式结构 使用 使用场景 适配器模式 简介 允许将不兼容的对象包装成一个适配器类，使得其他类可以通过适配器类与原始对象进行交互，从而提高兼容性 角色 目标角色…...

编程日记 2023/9/5 23:50:54

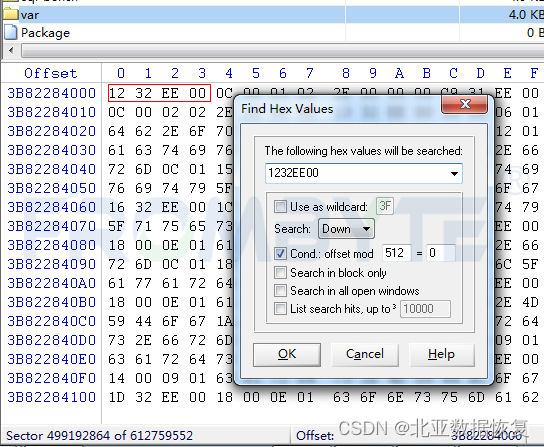
服务器数据恢复- Ext4文件系统分区挂载报错的数据恢复案例

Ext4文件系统相关概念： 块组：Ext4文件系统的空间被划分为若干个块组，每个块组内的结构大致相同。 块组描述符表：每个块组都对应一个块组描述符，这些块组描述符统一放在文件系统的前部，称为块组描述符表。每…...

编程日记 2023/9/5 23:49:53

19-springcloud(上)

一 微服务架构进化论 单体应用阶段 (夫妻摊位) 在互联网发展的初期，用户数量少，一般网站的流量也很少，但硬件成本较高。因此，一般的企业会将所有的功能都集成在一起开发一个单体应用，然后将该单体应用部署到一台服务器…...

编程日记 2023/9/5 23:48:53

前端基础---HTML笔记汇总一

HTML定义 HTML超文本标记语言——HyperText Markup Language。 超文本是什么&#xff1f; 链接标记是什么&#xff1f; 标记也叫标签&#xff0c;带尖括号的文本 标签分类 单标签:只有开始标签&#xff0c;没有结束标签(<br>换行 <hr>水平线 <img> 图像标…...

编程日记 2023/9/5 23:47:52

智汇云舟亮相中国安防工程商集成商大会

智汇云舟亮相中国安防工程商集成商大会&#xff0c;以视频孪生驱动安防行业数字化转型 近日&#xff0c;由中国安全防范产品行业协会指导&#xff0c;永泰传媒主办的中国安防工程商&#xff08;系统集成商&#xff09;大会暨第69届中国安防新产品、新技术成果展示在石家庄圆满…...

编程日记 2023/9/5 23:46:50

使用 Sealos 在离线环境中光速安装 K8s 集群

作者&#xff1a;尹珉。Sealos 开源社区 Ambassador&#xff0c;云原生爱好者。 当容器化交付遇上离线环境 在当今快节奏的软件交付环境中&#xff0c;容器化交付已经成为许多企业选择的首选技术手段。在可以访问公网的环境下&#xff0c;容器化交付不仅能够提高软件开发和交付…...

编程日记 2023/9/5 23:45:48

算法-模拟

1、旋转数组 public class Solution {/*** 代码中的类名、方法名、参数名已经指定&#xff0c;请勿修改&#xff0c;直接返回方法规定的值即可** 旋转数组* param n int整型 数组长度* param m int整型 右移距离* param a int整型一维数组 给定数组* return int整型一维数组*/…...

编程日记 2023/9/5 23:44:47

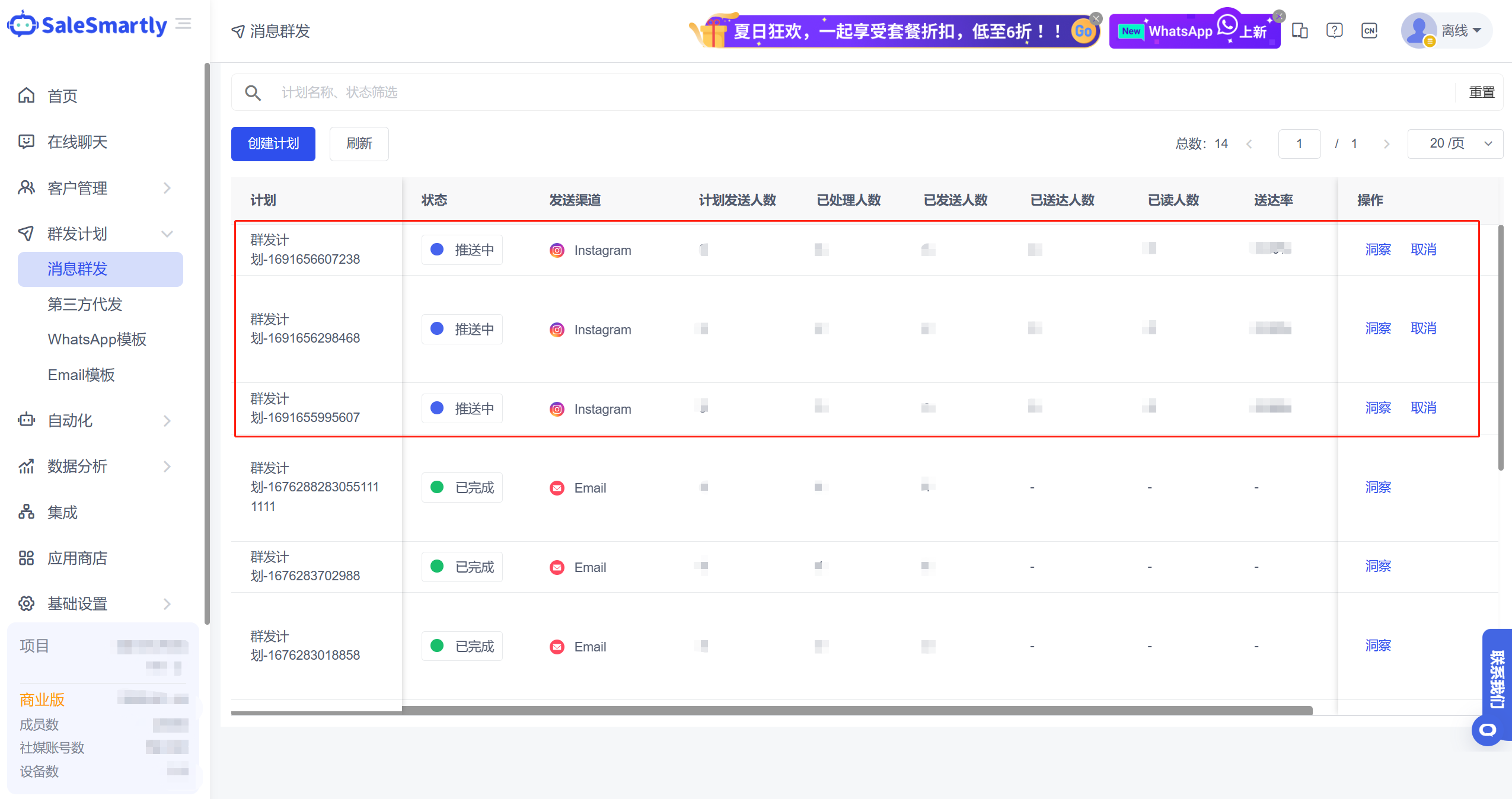
如何通过Instagram群发消息高效拓展客户？

之前小S有跟大家说过关于独立站&#xff0b;Instagram如何高效引流&#xff0c;发现大家都对Instagram的话题挺关注的。Instagram作为全球最受欢迎的社交媒体之一&#xff0c;对于许多商家和营销人员来说&#xff0c;Instagram是一个不可忽视的营销平台&#xff0c;他们可以通过…...

编程日记 2023/9/5 23:43:46

基于springboot实现多线程抢锁的demo

1、本代码基于定时调度和异步执行同时处理&#xff0c;如果只加异步处理&#xff0c;会导致当前任务未执行完&#xff0c;下个任务到点也不会触发执行 Scheduled(fixedRate 50_000)Asyncpublic void testThread() throws Exception{ZkLock lock new ZkLock(zkJob.getZK(), &q…...

编程日记 2023/9/5 23:42:46

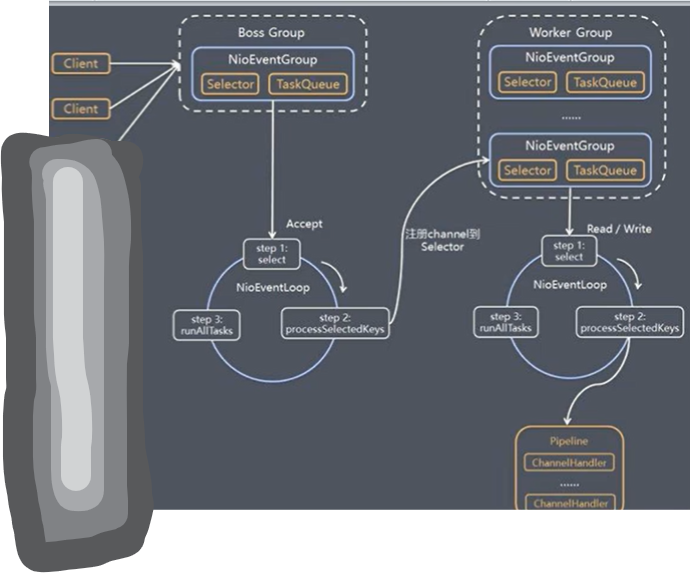
Java I/O模型发展以及Netty网络模型的设计思想

Java I/O模型发展以及Netty网络模型的设计思想 I/O模型Java BIOJava NIOJava AIO NIO Reactor网络模型单Reactor单线程模型单Reactor多线程模型主从Reactor多线程模型 Netty通信框架 前言&#xff1a; BIO、NIO的代码实践参考&#xff1a;Java分别用BIO、NIO实现简单的客户端服…...

编程日记 2023/9/5 23:41:44

智能电网时代：数字孪生的崭露头角

随着科技的不断进步&#xff0c;数字孪生已经开始在电力行业崭露头角&#xff0c;为这个关键的行业带来了前所未有的机遇和潜力。本文就带大家了解一下数字孪生在哪些方面为电力行业做出改变&#xff0c;以及未来的创新应用。 首先&#xff0c;数字孪生可以提高电力系统运营效率…...

编程日记 2023/9/5 23:40:43

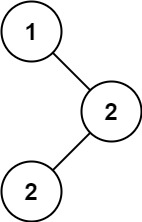
每日一题 501二叉搜素树中的众数（中序遍历）

题目 给你一个含重复值的二叉搜索树&#xff08;BST&#xff09;的根节点 root &#xff0c;找出并返回 BST 中的所有 众数&#xff08;即&#xff0c;出现频率最高的元素&#xff09;。 如果树中有不止一个众数&#xff0c;可以按 任意顺序 返回。 假定 BST 满足如下定义&a…...

编程日记 2023/9/5 23:39:42

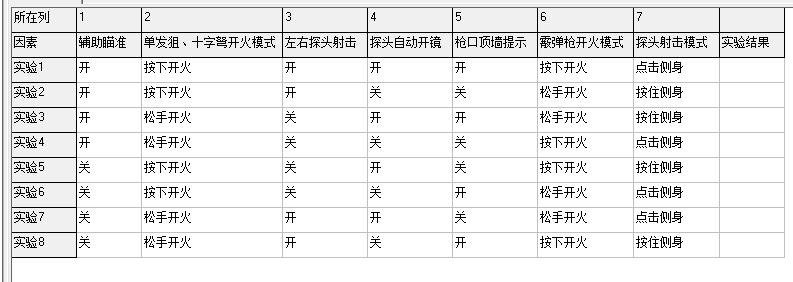
测试理论与方法----测试流程第三个环节：设计测试用例

测试流程第三个环节&#xff1a;设计测试用例&#xff1a;怎么测<——>测试需求的提取&#xff1a;测什么 ### 5、测试用例 描述&#xff1a;测试用例(TestCase)&#xff1a;是一份关于【具体测试步骤】的文档&#xff0c;是为了达到最佳的测试效果或高效揭露软件中潜藏的…...

编程日记 2023/9/5 23:38:39

C++多态案例2----制作饮品

#include<iostream> using namespace std;//制作饮品的大致流程都为&#xff1a; //煮水-----冲泡-----倒入杯中----加入辅料//本案例利用多态技术&#xff0c;提供抽象类制作饮品基类&#xff0c;提供子类制作茶叶和咖啡class AbstractDrinking {public://煮水//冲水//倒…...

编程日记 2023/9/5 23:37:38

机械零件保养3d模拟演示打消客户购买顾虑

复杂机械的工作运转是复杂的&#xff0c;想要对机械有深度的理解和迭代&#xff0c;必须了解它的运转原理及参数&#xff0c;复杂机械运行原因教学存在着不可视、系统庞杂及知识点多等弊病&#xff0c;3D虚拟展示是基于web3d网页运行的三维页面&#xff0c;可以将复杂机械运行过…...

编程日记 2023/9/5 23:36:37

SpringBoot的自动装配源码分析

文章目录 一&#xff1a;什么是自动装配二、springboot的启动流程1.调用SpringApplication&#xff08;&#xff09;的构造方法2.执行核心run方法&#xff08;&#xff09;3.执行核心prepareContext&#xff08;&#xff09;4.执行核心refreshContext&#xff08;&#xff09;5…...

编程日记 2023/9/5 23:35:36

Linux常用命令——csplit命令

在线Linux命令查询工具 csplit 将一个大文件分割成小的碎片文件 补充说明 csplit命令用于将一个大文件分割成小的碎片&#xff0c;并且将分割后的每个碎片保存成一个文件。碎片文件的命名类似“xx00”&#xff0c;“xx01”。csplit命令是split的一个变体&#xff0c;split只…...

编程日记 2023/9/5 23:34:35

React 组件的3大属性: state

state 一、理解二、用途三、使用3.1、类初始化3.2、函数初始化 四、状态读更4.1、组件内部状态管理和数据更新4.2、state 和 props 一起使用 一、理解 组件被称为"状态机", 页面的显示是根据组件的state 属性的数据来显示。 state 是一个用于存储和管理组件内部数据的…...

编程日记 2023/9/5 23:33:34

vscode 上传项目到gitlab

第一步初始化项目 如果没有创建过分支&#xff08;创建分支这里不记录&#xff09;&#xff0c;默认是master分支&#xff1a; ①将所需要的上传的文件添加到暂存区&#xff0c;如图&#xff1a; ②填写一下注释信息&#xff0c;将暂存区的文件上传到本地分支&#xff08;没有创…...

编程日记 2023/9/5 23:32:33

[羊城杯 2020] easyphp

打开题目&#xff0c;源代码 <?php$files scandir(./); foreach($files as $file) {if(is_file($file)){if ($file ! "index.php") {unlink($file);}}}if(!isset($_GET[content]) || !isset($_GET[filename])) {highlight_file(__FILE__);die();}$content $_GE…...

编程日记 2023/9/5 23:31:31

QT 常用类与组件

0 思维导图 1 信息调试类&#xff08;QDebug&#xff09; #include "widget.h" #include<iostream> //printf #include<QDebug> //qDebuf using namespace std; //coutWidget::Widget(QWidget *parent): QWidget(parent) {//输出函数//使用…...

编程日记 2023/9/5 23:30:29

C#控制台连接Mysql数据库，有配置数据库连接字符串的配置文件

C#控制台连接Mysql数据库&#xff0c;有配置数据库连接字符串的配置文件 实现功能 读取..txt 中的配置文件&#xff0c;来初始化连接字符串让连接字符串的配置文件不存在会主动创建默认的连接字符串 注意点&#xff1a; 需要引用Newtonsoft使用mysql 代码如下 using Syst…...

编程日记 2023/9/5 23:29:29

PowerBuilder连接SQLITE3

PowerBuilder,一个古老的IDE,打算陆续发些相关的,也许还有人需要,内容可能涉及其他作者,但基本都是基于本人实践整理,如涉及归属,请联系. SQLite,轻型数据库,相对与PowerBuilder来说是个新事务,故发数来,以供参考. PB中使用OLE Microsoft OLE DB方式进行连接,如下 // Profile…...

编程日记 2023/9/5 23:28:28