LeetCode_动态规划_困难_1326.灌溉花园的最少水龙头数目
目录
- 1.题目
- 2.思路
- 3.代码实现(Java)
1.题目
在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。
花园里总共有 n + 1 个水龙头,分别位于 [0, 1, …, n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ,其中 ranges[i] (下标从 0 开始)表示:如果打开点 i 处的水龙头,可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的最少水龙头数目。如果花园始终存在无法灌溉到的地方,请你返回 -1 。
示例 1:
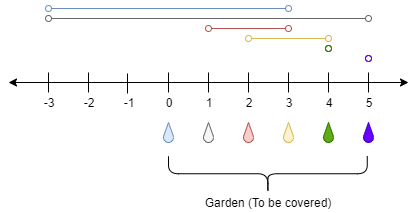
输入:n = 5, ranges = [3,4,1,1,0,0]
输出:1
解释:
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
示例 2:
输入:n = 3, ranges = [0,0,0,0]
输出:-1
解释:即使打开所有水龙头,你也无法灌溉整个花园。
提示:
1 <= n <= 104
ranges.length == n + 1
0 <= ranges[i] <= 100
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/minimum-number-of-taps-to-open-to-water-a-garden
2.思路
(1)动态规划
思路参考本题官方题解。
3.代码实现(Java)
//思路1————动态规划
class Solution {public int minTaps(int n, int[] ranges) {int[][] intervals = new int[n + 1][];for (int i = 0; i <= n; i++) {int start = Math.max(0, i - ranges[i]);int end = Math.min(n, i + ranges[i]);intervals[i] = new int[]{start, end};}/*此时题目转换为:从 [start0, end0]、[start1, end1]、...、[startn, endn] 中选出最少数目的区间,使得它们可以覆盖 [0, n]*///将所有区间按照起点进行升序排序Arrays.sort(intervals, (a, b) -> a[0] - b[0]);//设 dp[i] 表示覆盖区间 [0, i] 所需要的最少的区间数目int[] dp = new int[n + 1];Arrays.fill(dp, Integer.MAX_VALUE);dp[0] = 0;for (int[] interval : intervals) {int start = interval[0];int end = interval[1];if (dp[start] == Integer.MAX_VALUE) {return -1;}for (int j = start; j <= end; j++) {dp[j] = Math.min(dp[j], dp[start] + 1);}}return dp[n];}
}
相关文章:

LeetCode_动态规划_困难_1326.灌溉花园的最少水龙头数目
目录1.题目2.思路3.代码实现(Java)1.题目 在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。 花园里总共有 n 1 个水龙头,分别位于 [0, 1, …, n] 。 给你一个整数 n 和一个长度为 n 1 的整数数…...
mac tcpdump学习
学习原因 工作上遇到了重启wifi后无法发出mDNS packet的情况,琢磨一下用tcpdump用的命令如下 sudo tcpdump -n -k -s 0 -i en0 -w VENDOR-DUT-INTERFACE.pcapng是在测airplay BCT认证时,官方文档的解决方法。对tcpdump很不了解,现汇总如下的学…...

【跟我一起读《视觉惯性SLAM理论与源码解析》】第二章 编程及编译工具
23.2.21终于拿到六哥的新书 感觉很是不错,打算近期写一写心得之类的 废话不多说,直接开啃 PS:我的建议是阅读完十四讲后再来看这本书,效果应该会很不错。 因为第一章都是介绍之类的我觉得没什么整理的必要,所以直接来…...

广东望京卡牌科技有限公司,2023年团建活动圆满举行
玉兔初临,春天相随,抖擞精神,好运连连。春天是一个万物复苏的季节,来自广东的望京卡牌科技有限公司,也迎来了新年第一次团建活动。在“乘风破浪、追逐梦想”的口号声中,2023望京卡牌目标启动会团结活动正式…...

ts语法如何在Vue3中运用?
一、父子传值的用法 父传子:defineProps的TS写法 // 父组件:和 vue2 一样正常传值 <template><div class"login-page"><cp-nav-bar title"登录" right-text"注册"></cp-nav-bar></div> &…...

RK3566添加湿度传感器以及浅析hal层
RK3566添加一款温湿度传感器gxht3x.挂在i2c总线下。驱动部分就不多做解析。大致流程硬件接好i2c线以及vcc gnd。后看数据手册。初始化寄存器,然后要读数据的话读那个寄存器,读出来的数据要做一个转化,然后实现open read write ioctl函数就行了。本文主要…...
看了这份Java高级笔试宝典覆盖近3年Java笔试中98%高频知识点,反打面试官
首先声明: 本书覆盖了近3年程序员面试笔试中超过98%Java高频知识点,当你细细品读完本书后,面试都是小问题。 一书在手/工作不愁 记住重点,考试要考 前言 程序员求职始终是当前社会的一个热点,而市面上有很多关于程…...
从0到1搭建大数据平台之监控
大家好,我是脚丫先生 (o^^o) 大数据平台设计中,监控系统尤为重要。 它时刻关乎大数据开发人员的幸福感。 试想如果半夜三更,被电话吵醒解决集群故障问题,那是多么的痛苦!!! 但是不加班是不可…...

采购评标管理过程是怎样的?有哪些评标标准?
采购活动的评标是检查和比较投标的有组织的过程,以选择最佳报价,努力获得实现企业目标所需的货物、工程和服务。 评标是由一个被称为评标小组的机构负责。这个小组如何称呼,取决于企业的情况。同义词有报价审查小组、投标审查委员会或投标审…...
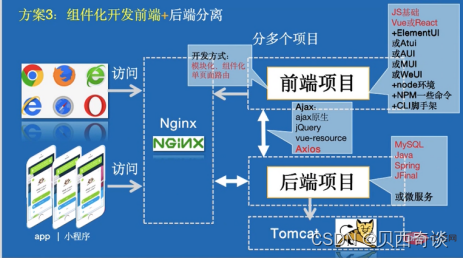
《Vue+Spring Boot前后端分离开发实战》专著累计发行上万册
杰哥的学术专著《VueSpring Boot前后端分离开发实战》由清华大学出版社于2021年3月首次出版发行,虽受疫情影响但热度不减,受到业界读者的热捧,截至今日加印5次,累计发行12000册,引领读者开发前后端分离项目,…...

类与类之间的关系有哪几种?
文章目录程序设计要素1.可读性2.健壮性3.优化4.复用性5.可扩展性设计类的关系遵循的原则1、 高内聚低耦合2、面向对象开发中 “针对接口编程优于针对实现编程”,”组合优于继承” 的总体设计类与类之间的关系(即事物关系) A is-a B 泛化&…...

LeetCode 606.根据二叉树创建字符串,102.二叉树的层序遍历和牛客 二叉搜索树与双向链表
文章目录1. 根据二叉树创建字符串2. 二叉树的层序遍历3. 二叉搜索树与双向链表1. 根据二叉树创建字符串 难度 简单 题目链接 解题思路: 这里的意思就是:用前序遍历遍历这颗树。然后左子树和右子树分别在一个括号里。括号里的规则是: 1.左右都…...
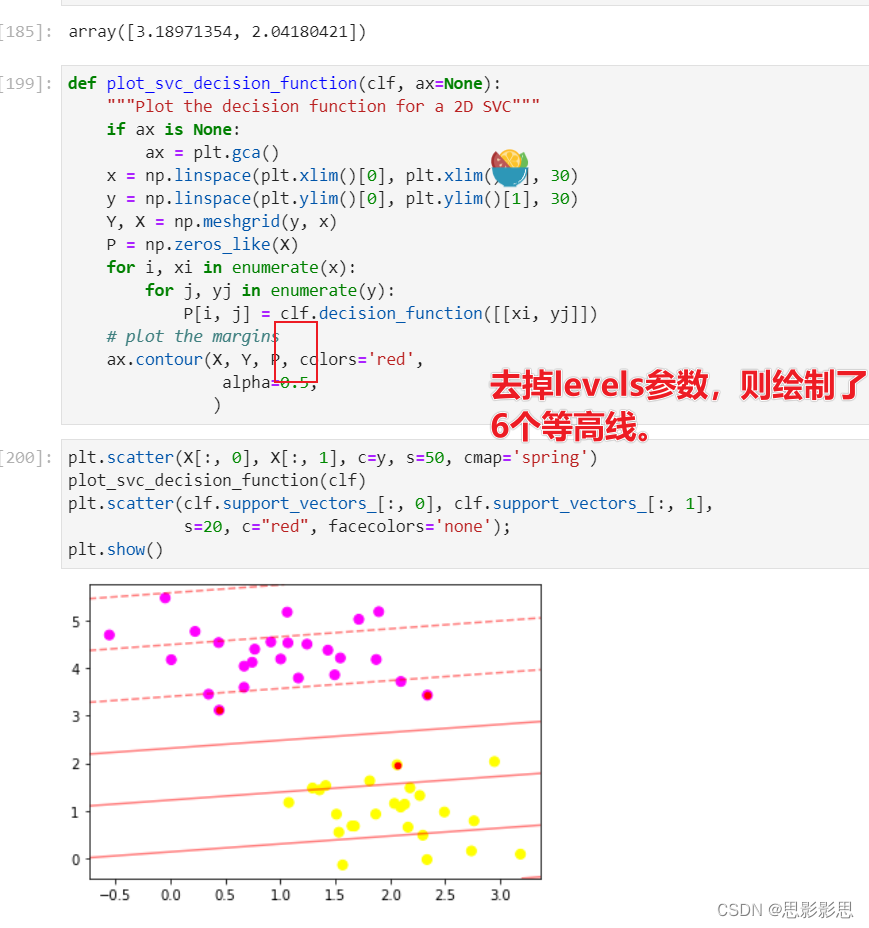
02-18 周六 图解机器学习之SMV 第五章5-2
02-18 周六 图解机器学习之SMV 第五章5-2时间版本修改人描述2023年2月18日11:47:18V0.1宋全恒新建文档 环境 程序的基本环境,是使用了jupyter,在容器中运行的。 简介 本程序主要演示支持向量的获取,支持向量是距离超平面最近的点组成的。程序…...
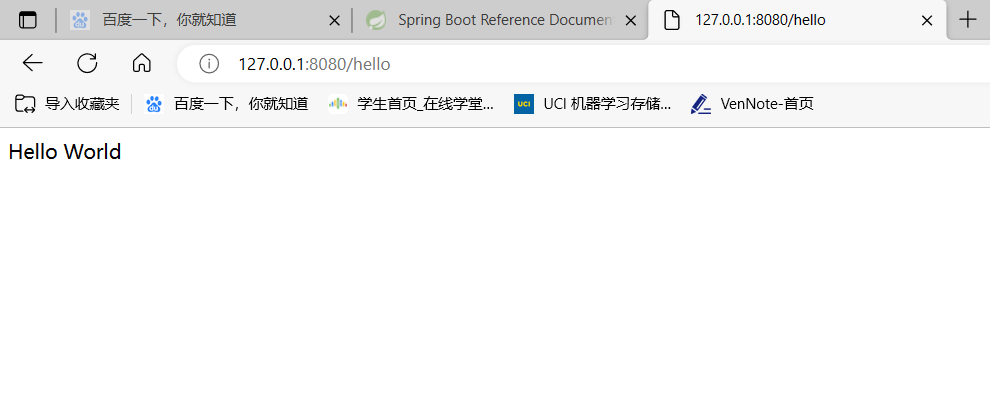
Spring Boot系列--创建第一个Spring Boot项目
1.项目搭建 在IDEA中新建项目,选择Spring Initializr。 填写项目信息: 选择版本和Spring Web依赖: Spring Web插件能为项目集成Tomcat、配置dispatcherServlet和xml文件。此处选择的版本若为3.0.2的话会出现如下错误: java: …...

手把手教你用React Hook和TypeScript从零实现虚拟滚动列表组件
前言 k8s 全称 kubernetes,这个名字大家应该都不陌生,k8s是为容器服务而生的一个可移植容器的编排管理工具,集应用的部署和运维,负载均衡,服务发现和扩容,版本回滚于一身,越来越多的公司正在拥…...
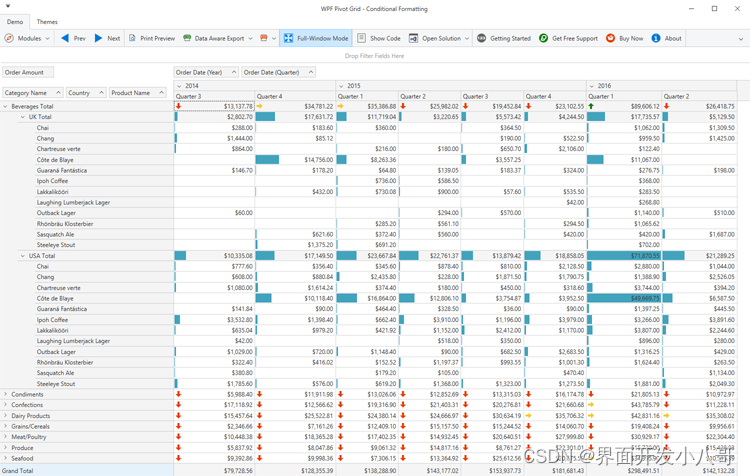
界面控件DevExpress WPF Pivot Grid——拥有强大多维数据分析能力!
界面控件DevExpress WPF的Pivot Grid组件是一个类似excel的数据透视表,用于多维数据分析和跨选项卡报表生成。它拥有众多的布局自定义选项,允许开发者完全控制其UI且以用户为中心的功能使其易于部署。PS:DevExpress WPF拥有120个控件和库&…...

python字典及基础操作
1) 字典是没有顺序的,是任意对象的无序集合。 2) 字典的键是唯一的,不能多次出现,多次出现时取最后一个值。 3) 键是不可变的。 4) 字典中的元素可增删。 5) 因为没有顺序,所以不存在索引。 1. 字典元素的访问 >>> …...
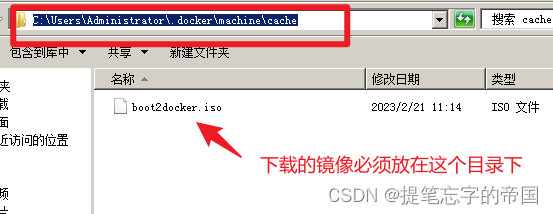
Windows Server 2008 R2安装onlyoffice【docker】
目录 前言 准备工作 安装docker 安装onlyoffice 常见问题 前言 目前docker for windows只能在windows10/11上安装,其他的windows版本只能使用Docker Toolbox来安装,使用该工具安装的docker其实是借助了Oracle VM VirtualBox虚拟机来运行的&a…...
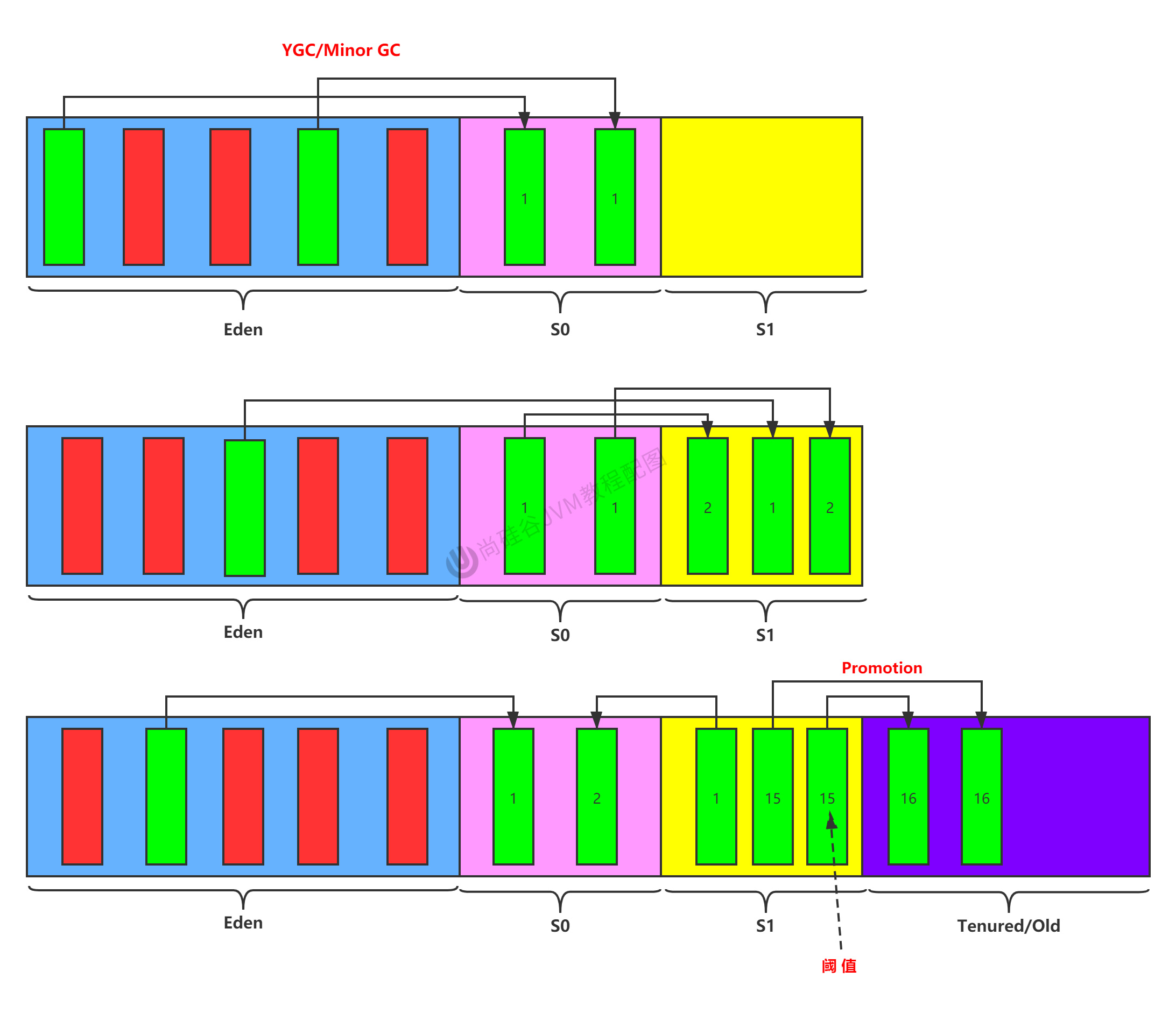
JVM学习笔记六:运行时数据区之堆
目录 概述 堆空间内部结构 JDK7版本 JDK8版本 堆空间的内存划分 堆空间大小设置参数 概述 Java堆是虚拟机所管理的内存中最大的一块,其在JVM启动时即被创建,并且空间大小也被确定(这里是不考虑Java8之后以本地内存来实现的元空间&…...
usb闪存驱动器数据恢复该怎么进行?3个方法总结
“怎么办?我的USB驱动器不知道因为什么原因,里面的数据、文件都消失了。有没有什么方法在没有进行备份的情况下恢复从U盘丢失的数据?” USB驱动器作为最常用的存储移动设备,里面保存着各种文件数据。但是有时会出现损坏而导致数据…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
