2020 杭电多校第三场 H Triangle Collision(反射套路 + 绕点旋转 + 矢量
2020 杭电多校第三场 H. Triangle Collision(反射套路 + 绕点旋转 + 矢量分解)
大意:给出一个等边三角形 , 以底边中线建立坐标系 , 给出三角形中一点 , 和其初始速度 , 小球在等边三角形中做完全弹性碰撞 , 问其恰好碰撞 k 次的时间。
解法:
trick1: 反射套路
对于这样一个反射套路题 , 如果模拟在一个三角形内模拟碰撞的话 , 显然不现实 ,所以我们可以根据反射原理 , 将路径变成一条直线。这样问题就变成了射线在下图中的交点个数问题。

trick2: 我们不妨先思考水平直线相交个数如何求。假设运动实现为 t 那么显然交点个数就是
a b s ( f l o o r ( y + v y t h ) ) abs(floor(\frac{y+v_yt}{h})) abs(floor(hy+vyt))
对于另外两种直线 , 我们要求相应坐标系下的 y 和 vy
对于 y(标量) 的求法有两种 , 第一种是用点到直线的距离公式 , 但是点到直线距离公式中有除法 , 误差很大 , 所以精度不够。
第二种方法是我们可以把操作转化成绕三角形中心旋转坐标系 , 对应点的坐标也绕中心旋转后即是答案。
trick3:
对于 vy(矢量) , 我们设立好正方向 , 进行矢量分解即可。一定要设立正方向 , 因为矢量是有方向的。
这样就能求得某一时刻 t 穿过点数量 , 二分一下 t 即可。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;//--------------------------------------------------------------
const double eps = 1e-5;
const double pi = acos(-1);
inline double sqr(double x) {return x * x;} //平方
int sign(double x){if(fabs(x) < eps) return 0;if(x > 0) return 1;return -1;
}//符号
struct point{double x , y;point(){}point(double a , double b) : x(a) , y(b){}friend point operator + (const point &a , const point &b){return point(a.x + b.x , a.y + b.y);}friend point operator - (const point &a , const point &b){return point(a.x - b.x , a.y - b.y);}friend bool operator == (const point &a , const point &b){return !sign(a.x - b.x) && !sign(a.y - b.y);}friend point operator * (const point &a , const double &b){return point(a.x * b , a.y * b);}friend point operator * (const double &a , const point &b){return point(a * b.x , a * b.y);}friend point operator / (const point &a , const double &b){return point(a.x / b , a.y / b);}//向量模长 double norm(){ return sqrt(sqr(x) + sqr(y));}
}; //坐标轴绕某点旋转后 , 原坐标轴下的点也会绕这个点旋转
double rotate_point(const point &a , const point &p , double A){double tx = p.x - a.x , ty = p.y - a.y;return a.y + tx * sin(A) + ty * cos(A);
}// p 点 绕 a 点逆时针旋转 A 弧度
//--------------------------------------------------------------int t , k;
double h , x , y , vx , vy , yr , yl;int solve(double st , double v , double t){return abs(floor((st + v * t) / h));
}bool check(double t){int res = 0;res += solve(y , vy , t);//水平res += solve(yr , (vx * sqrt(3) - vy) / 2 , t);res += solve(yl , (-vx * sqrt(3) - vy) / 2 , t);return res >= k;
}signed main(){cout << fixed << setprecision(10);cin >> t;while(t --){cin >> h >> x >> y >> vx >> vy >> k;h = h * sqrt(3) / 2;yr = rotate_point(point{0 , h / 3} , point{x , y} , pi / 3 * 2);yl = rotate_point(point{0 , h / 3} , point{x , y} , pi / 3 * 4);double l = 0 , r = 1e9 , mid = 0;while(r - l > eps){mid = (l + r) / 2;if(check(mid)) r = mid;else l = mid;}cout << mid << "\n"; }return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:

2020 杭电多校第三场 H Triangle Collision(反射套路 + 绕点旋转 + 矢量
2020 杭电多校第三场 H. Triangle Collision(反射套路 绕点旋转 矢量分解) 大意:给出一个等边三角形 , 以底边中线建立坐标系 , 给出三角形中一点 , 和其初始速度 , 小球在等边三角形中做完全弹性碰撞 , …...
Servlet属性、监听者和会话
没有servlet能单独存在。在当前的现代Web应用中,许多组件都是在一起协作共同完成一个目标。怎么让这些组件共享信息?如何隐藏信息?怎样让信息做到线程安全? 1 属性和监听者 1.1 初始化 容器初始化一个servlet时,会为…...

Gin学习记录2——路由
路由 一. 常规路由二. 动态路由三. 带参数的路由3.1 GET3.2 POST3.3 绑定 四. 简单的路由组五. 文件分组 一. 常规路由 package mainimport ("net/http""github.com/gin-gonic/gin" )func index(ctx *gin.Context) {ctx.String(http.StatusOK, "Hell…...

《计算机算法设计与分析》第一章:算法概述
第一章 算法概述 1.1 算法复杂性分析 公共标准:渐进时间复杂度 (1)大O表示法: 例如: 大O表示法和前面的最坏时间复杂度的区别在于:大O表示法表示的更为简洁, 而最坏时间复杂度相对就比较繁琐&am…...

华为数通方向HCIP-DataCom H12-821题库(单选题:201-220)
第201题 BGP 协议用 beer default-route-advertise 命令来给邻居发布缺省路由,那么以下关于本地 BGP 路由表变化的描述,正确的是哪一项? A、在本地 BGP 路由表中生成一条活跃的缺省路由并下发给路由表 B、在本地 BGP 路由表中生成一条不活跃的缺省路由&…...
使用ELK收集解析nginx日志和kibana可视化仪表盘
文章目录 ELK生产环境配置filebeat 配置logstash 配置 kibana仪表盘配置配置nginx转发ES和kibanaELK设置账号和密码 ELK生产环境配置 ELK收集nginx日志有多种方案,一般比较常见的做法是在生产环境服务器搭建filebeat 收集nginx的文件日志并写入到队列(k…...
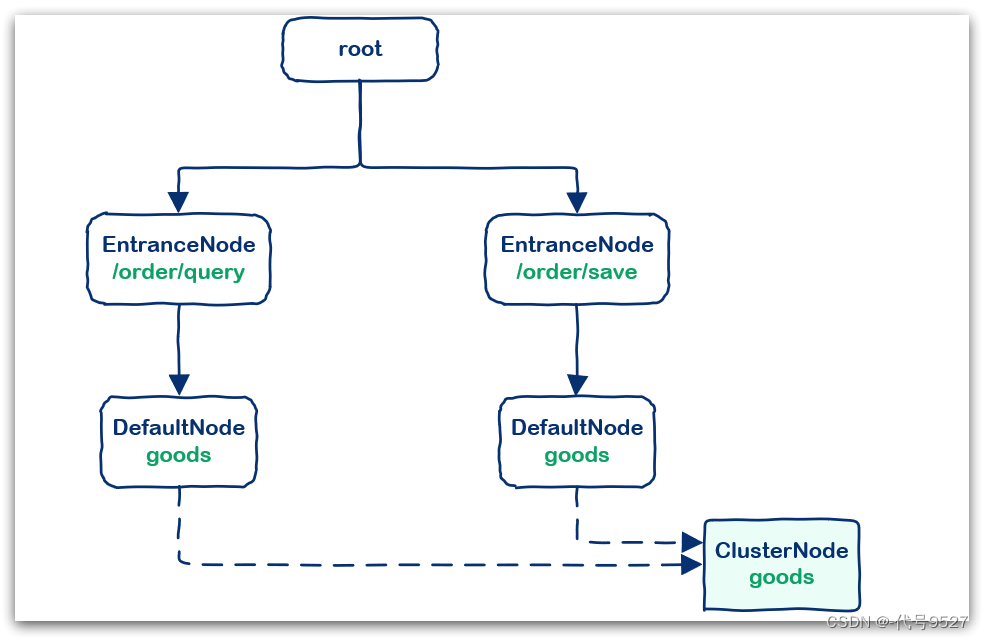
【Sentinel】ProcessorSlotChain处理器插槽链与Node
文章目录 1、Sentinel的基本概念2、ProcessorSlotChain3、Node 1、Sentinel的基本概念 Sentinel实现限流、隔离、降级、熔断等功能,本质要做的就是两件事情: 统计数据:统计某个资源的访问数据(QPS、RT等信息)规则判断…...
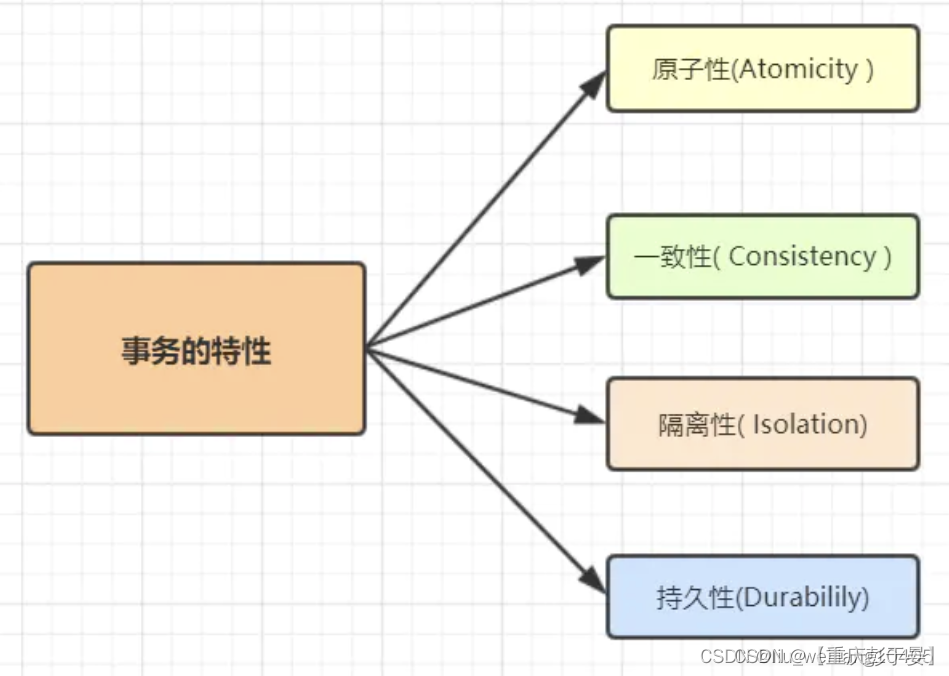
数据库管理系统(DBMS)的事务四大特性(ACID)以及事务的四种隔离级别
一、什么是ACID? ACID是原子性(Atomicity)、一致性(Consistency)、隔离性(Isolation)和持久性(Durability) 的缩写,是在可靠数据库管理系统(DBMS&…...
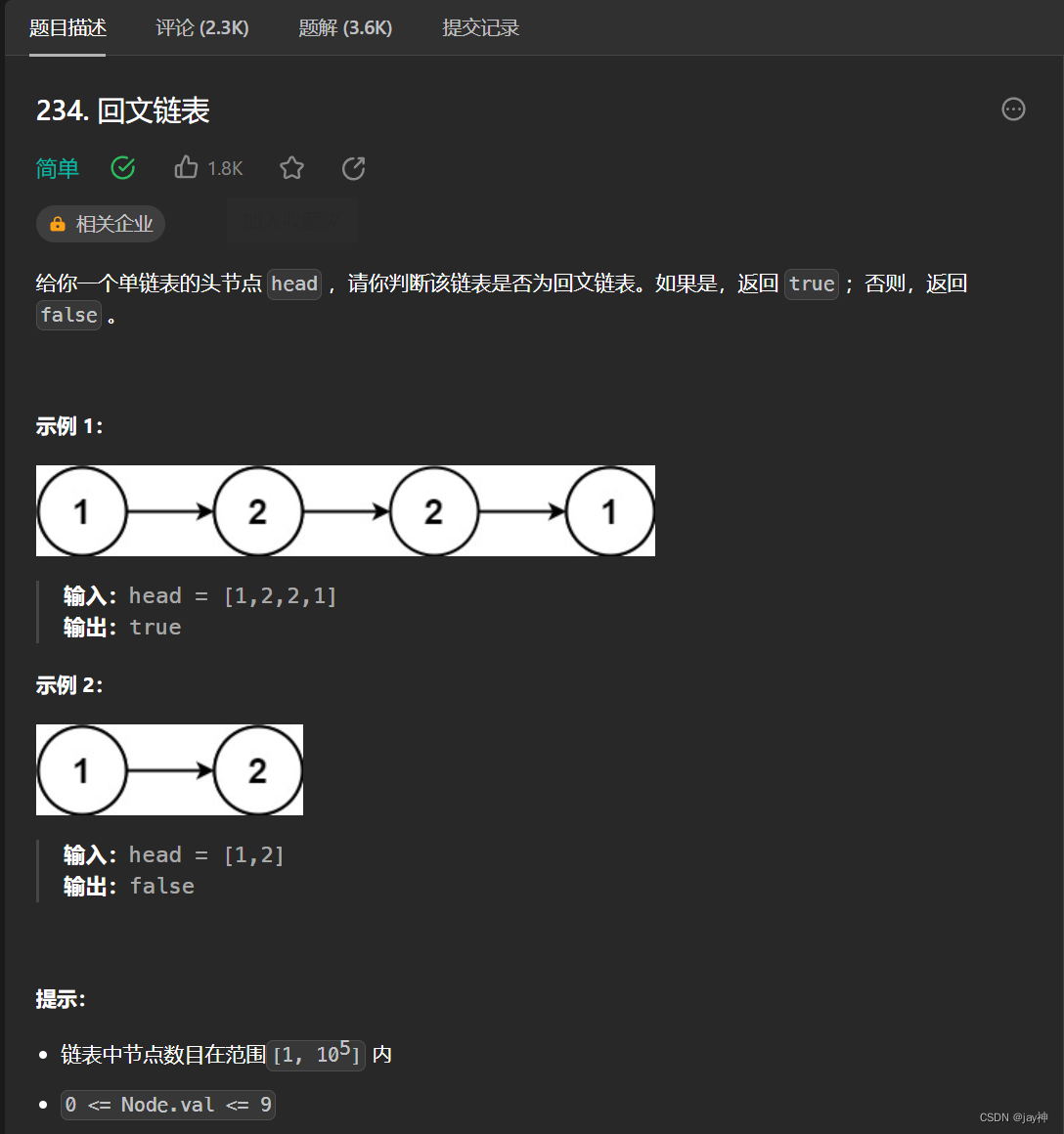
leetcode 234. 回文链表
2023.9.5 本题先将链表的节点值移到数组中,再用双指针去判断该数组是否为回文的即可。 代码如下: /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* …...

Scala集合继承体系图
Scala集合简介 1) Scala 的集合有三大类:序列 Seq、集Set、映射 Map,所有的集合都扩展自 Iterable特质。 2) 对于几乎所有的集合类,Scala 都同时提供了可变和不可变的版本,分别位于以下两个包 不可变集合…...
)
《Go 语言第一课》课程学习笔记(十五)
并发 Go 的并发方案:goroutine 并行(parallelism),指的就是在同一时刻,有两个或两个以上的任务(这里指进程)的代码在处理器上执行。 并发不是并行,并发关乎结构,并行关…...

练习 Qt 实时显示鼠标坐标位置
Qt 入门实战教程(目录) 前驱课程 本文是文章 Qt鼠标点击事件处理:显示鼠标点击位置(完整示例) 的一个作业(下文称之为“前驱课程”)。 前驱课程中,我们完整的展示了如何在QtCreat…...
Leetcode130. 被围绕的区域
Every day a Leetcode 题目来源:130. 被围绕的区域 本题给定的矩阵中有三种元素: 字母 X;被字母 X 包围的字母 O;没有被字母 X 包围的字母 O。 本题要求将所有被字母 X 包围的字母 O都变为字母 X ,但很难判断哪些 …...
6.xpath的基本使用
xpath是python做数据解析的库 目录 1 安装 2 解析本地的html文件 2.1 只有一个标签的情况 2.2 有多个标签的情况 3 解析网上的页面 4 xpath表达式 4.1 绝对路径 4.2 两个斜杠表示中间隔了0级或多级 4.3 通过属性查找 4.4 通过索引查找 4.5 获取文本内容…...

uniapp组件库总结笔记
uView-ui uView 2.0 - 全面兼容 nvue 的 uni-app 生态框架 - uni-app UI 框架 优点:整体样式风格不错 缺点:不支持vue3(可以使用社区维护的uview-plus uview-plus 3.0 - 全面兼容nvue的uni-app生态框架 - uni-app UI框架) uni-u…...

day-42 代码随想录算法训练营 动态规划 part 04
416.分割等和子集 分析:需要总和能分成两半,并且有子集能装满一半 思路: 1.dp存储:容量为j时装入的最大数值和dp[j]2.dp[j]max(dp[j],dp[j-nums[i]]nums[i]) 3.全部初始化为04.遍历顺序:外层遍历元素,内…...

Swift 周报 第三十六期
文章目录 前言新闻和社区消息称苹果公司和印度财政部官员磋商,扩大在印度的制造产能iPhone 15 Pro 机型新增泰坦灰iPhone 15 全系配 USB-C 苹果拒绝接口和安卓互通 提案正在审查的提案 Swift论坛推荐博文话题讨论关于我们 前言 本期是 Swift 编辑组整理周报的第三十…...

手写Mybatis:第19章-二级缓存
文章目录 一、目标:二级缓存二、设计:二级缓存三、实现:二级缓存3.1 工程结构3.2 二级缓存类图3.3 二级缓存队列3.3.1 FIFI缓存策略3.3.2 事务缓存3.3.3 事务管理3.3.4 修改一级缓存 3.4 缓存执行器3.4.1 执行器接口3.4.2 执行器抽象基类3.4.…...

Alibaba Canal 使用记录
项目中使用 canal 来同步数据到 Elasticsearch, 遇到很多问题,做一下记录: 版本问题: 1. 解析binlog出错 ,表现为 limit excceed:xx 目前使用 mariadb 10.9.7/10.10.6 canal 1.1.6 hotfix ,在这个版本组…...
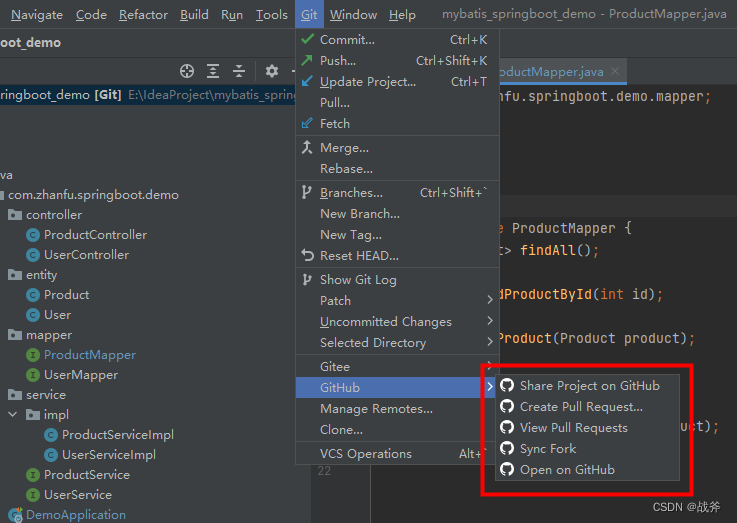
GIT实战篇,教你如何使用GIT可视化工具
系列文章目录 手把手教你安装Git,萌新迈向专业的必备一步 GIT命令只会抄却不理解?看完原理才能事半功倍! 快速上手GIT命令,现学也能登堂入室 GIT实战篇,教你如何使用GIT可视化工具 系列文章目录一、GIT有哪些常用工具…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
