题目:2644.找出可整除性得分最大的整数
题目来源:
leetcode题目,网址:2644. 找出可整除性得分最大的整数 - 力扣(LeetCode)
解题思路:
遍历计算即可。
解题代码:
class Solution {public int maxDivScore(int[] nums, int[] divisors) {int score=0;int res=divisors[0];for(int divisor:divisors){int thisScore=0;for(int num:nums){if(num%divisor==0){thisScore++;}}if(thisScore>score || (thisScore==score && divisor<res)){score=thisScore;res=divisor;}}return res;}
}总结:
无官方题解。
相关文章:

题目:2644.找出可整除性得分最大的整数
题目来源: leetcode题目,网址:2644. 找出可整除性得分最大的整数 - 力扣(LeetCode) 解题思路: 遍历计算即可。 解题代码: class Solution {public int maxDivScore(int[] nums, int[] di…...
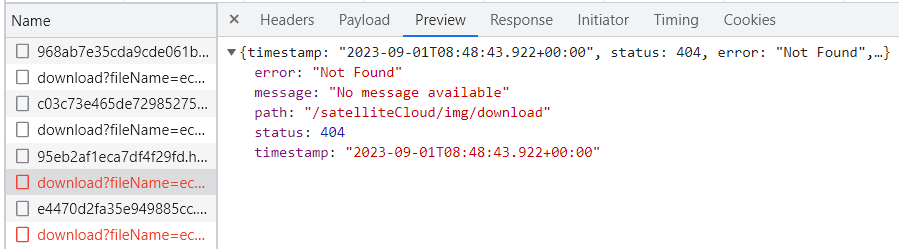
报错:axios 发送的接口请求 404
axios 发送的接口请求 404 一、问题二、分析 一、问题 二、分析 axios 发送的接口请求 404,根本没有把接口信息发送到后端,这个时候你可以查看检查一下自己的接口名字,或让后端配合换一个接口名字再发送一次接口请求...

三年前端还不会配置Nginx?刷完这篇就够了
什么是Nginx Nginx是一个开源的高性能HTTP和反向代理服务器。它可以用于处理静态资源、负载均衡、反向代理和缓存等任务。Nginx被广泛用于构建高可用性、高性能的Web应用程序和网站。它具有低内存消耗、高并发能力和良好的稳定性,因此在互联网领域非常受欢迎。 为…...
blender 场景灯光基础设置
在 blender 中,打光分为两个部分,一个是世界光,一个是场景光; 世界光: 世界光:在 Blender 中,世界光指的是用于设置场景整体照明的环境光。它可以通过调整颜色、强度、阴影等参数来影响场景的…...
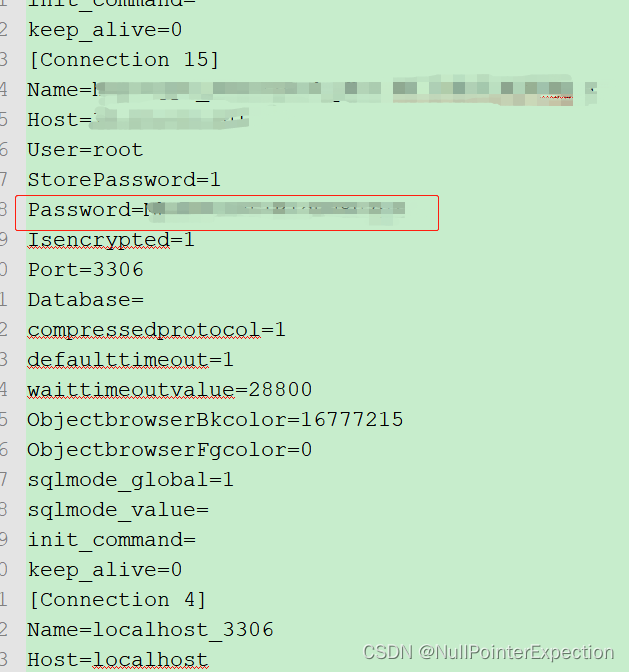
如何查看 SQLyog 中数据库连接信息中的密码
SQLyog 数据库连接信息中的密码无法选择明文展示,也无法复制 可以将数据库连接信息导出到文本查看明文密码 工具--》导入/导出连接详情:...
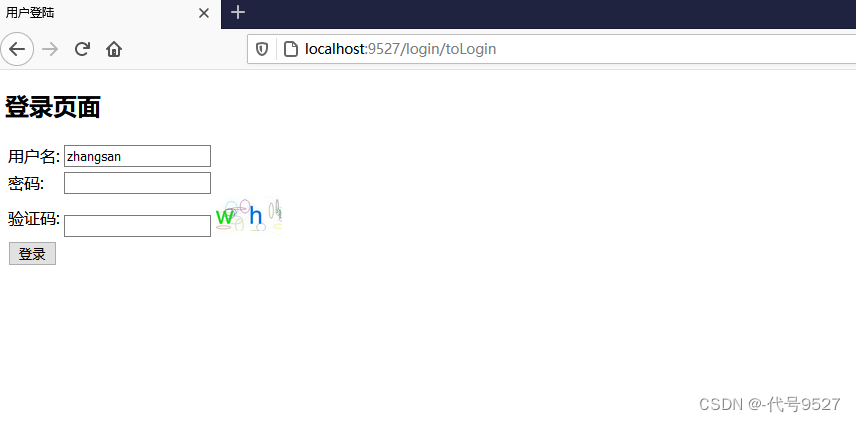
【SpringSecurity】八、集成图片验证码
文章目录 1、生成图片验证码2、创建验证码过滤器3、将过滤器加入SpringSecurity过滤链4、修改登录页 SpringSecurity是通过过滤器链来完成的,接下来的验证码,可以尝试创建一个过滤器放到Security的过滤器链中,在自定义的过滤器中比较验证码。…...
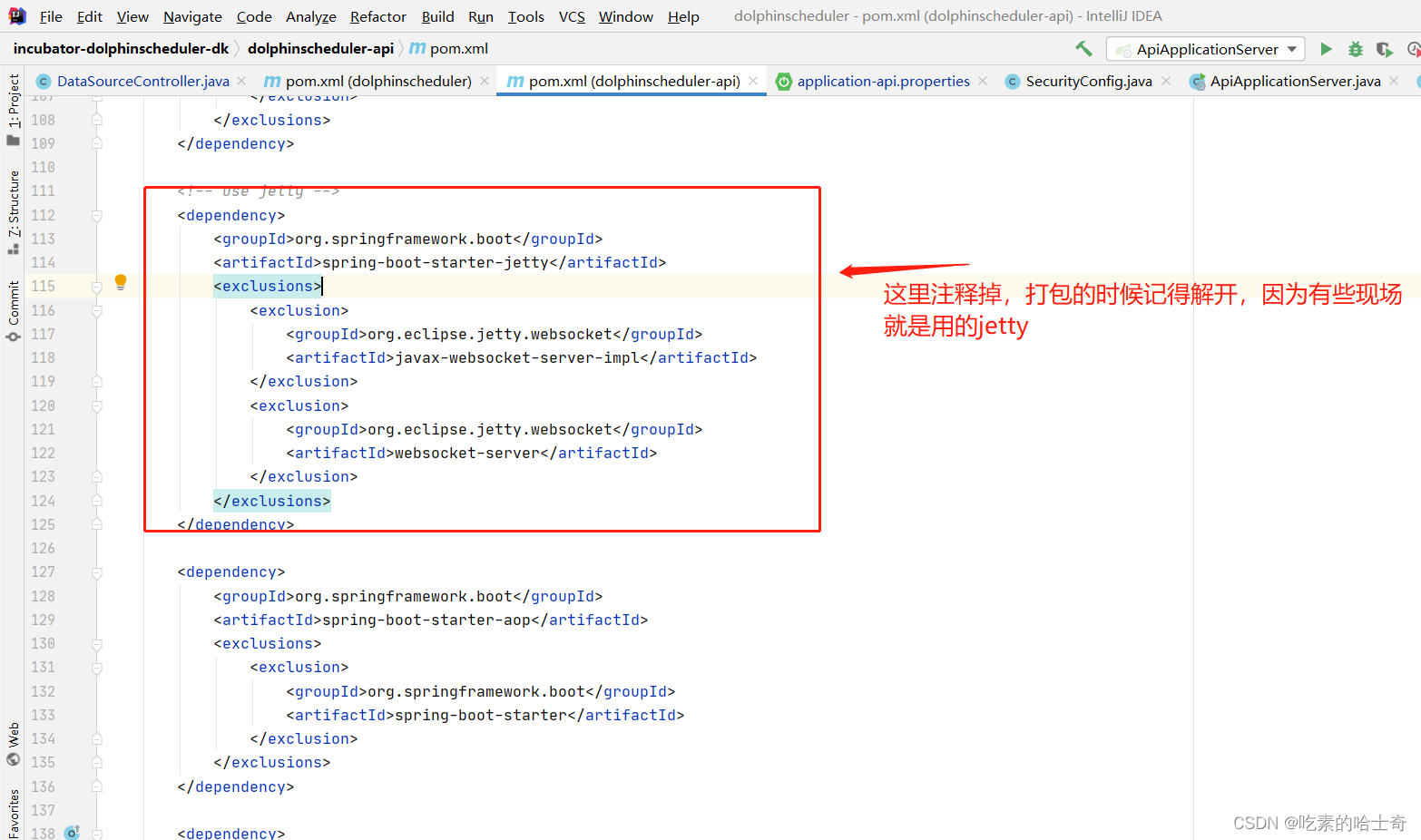
【本地代码问题】启动程序,报错:java.lang.IllegalArgumentException: No selectors
启动程序的时候报错了 问题怎么出现的解决方式,注释掉jetty的内容,回归tomcat的使用 问题怎么出现的 我本地启动程序的时候报错了:报的是这个错误,可能和容器的选择有关吧 解决方式,注释掉jetty的内容,回…...
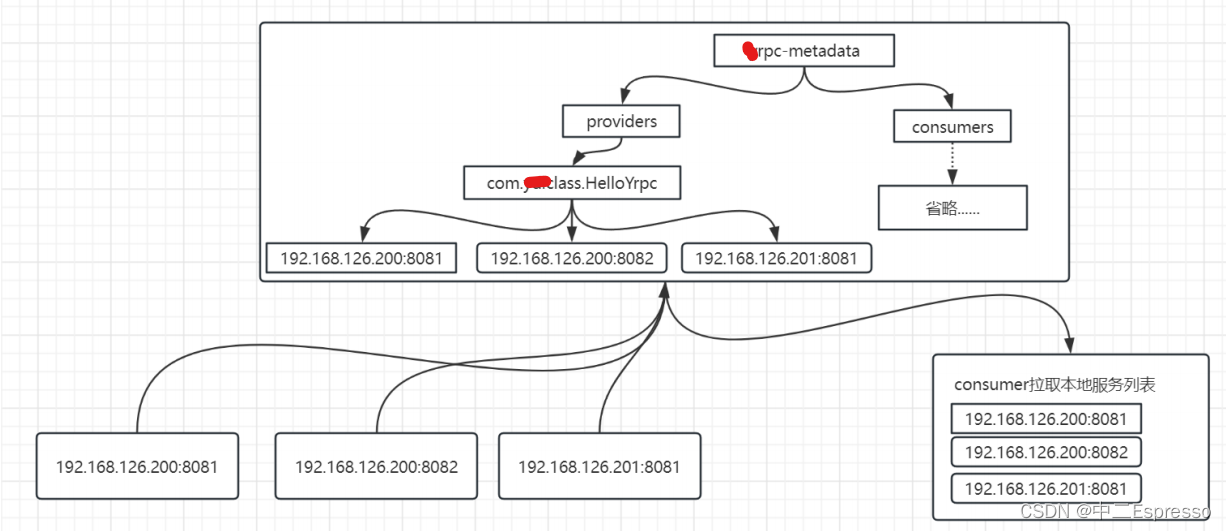
手写RPC框架--4.服务注册
RPC框架-Gitee代码(麻烦点个Starred, 支持一下吧) RPC框架-GitHub代码(麻烦点个Starred, 支持一下吧) 服务注册 服务注册a.添加服务节点和主机节点b.抽象注册中心c.本地服务列表 服务注册 a.添加服务节点和主机节点 主要完成服务注册和发现的功能,其具体流程如下&…...

oracle 解锁表
操作的前提 用 sys 用户 以 SYSDBA 角色登录 第一种解锁方式 1.查询被锁的表 select object_name,machine,s.sid,s.serial# from v$locked_object l,dba_objects o ,v$session s where l.object_id o.object_id and l.session_ids.sid;2.查询那个session引起表被锁 sele…...

使用Dbeaver连接GaussDB
1.下载DBeaver,官网地址 2.安装软件,打开软件,点击数据库->驱动管理器,具体操作如下图: 3、选择新建后进行参数设置,如下图: 具体参数如下图 驱动名称: GS #随便定义 驱动类型&#…...
WSL使用技巧 / 虚拟机对比
WSL使用技巧 / 虚拟机对比 前言虚拟机比较VMware使用技巧WSL使用技巧官方文档工具安装WSL基本命令运行命令关闭卸载磁盘管理导入导出指定安装路径 前言 本文介绍了VMware和WSL的区别,并详细介绍了WSL的使用方法和技巧。 虚拟机比较 VMware 比较灵活,拥…...

vuex_cart案例
json-server使用 在目录下新建db文件夹>里面新建index.json index.json {"cart": [{"id": 100001,"name": "低帮城市休闲户外鞋天然牛皮COOLMAX纤维","price": 128,"count": 6,"thumb": "http…...
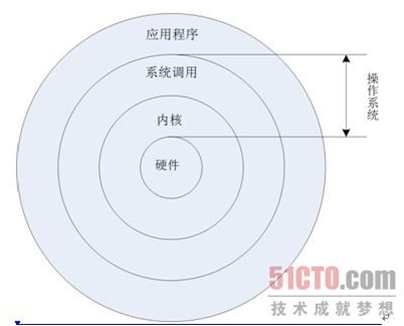
Linux系统的安装
文章目录 1 Linux介绍1.1 Linux是什么1.2 Linux的特点1.3 Linux的应用1.4 Linux的发行版本1.5 Linux的Shell 2 Linux安装2.1 安装方式2.2 什么是VMware2.3 VMware主要功能2.4 什么是CentOS2.5 VMware与CentOS与Linux的关系2.6 VMware安装CentOS的步骤 1 Linux介绍 1.1 Linux是…...
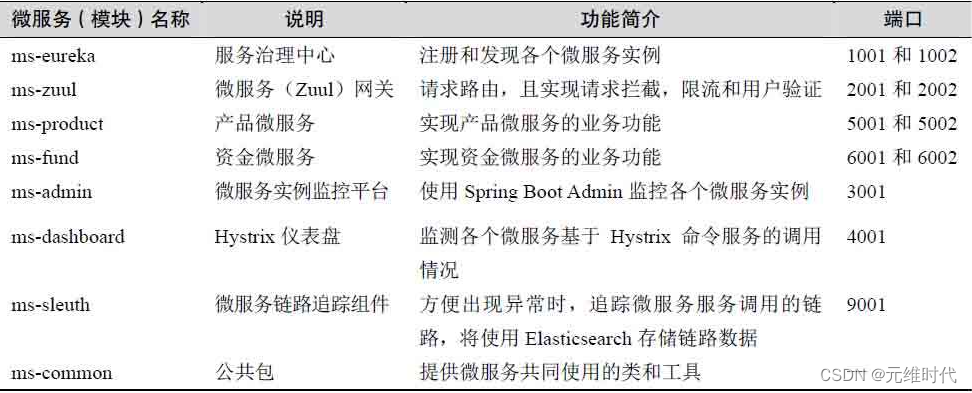
微服务设计和高并发实践
文章目录 1、微服务的设计原则1.1、服务拆分方法1.2、微服务的设计原则1.3、微服务架构 2、高并发系统的一些优化经验2.1、提高性能2.1.1、数据库优化2.1.2、使用缓存2.1.3、服务调用优化2.1.4、动静分离2.1.5、数据库读写分离 2.2、服务高可用2.2.1、限流和服务降级2.2.2、隔离…...

2023年高教社杯数学建模思路 - 案例:粒子群算法
文章目录 1 什么是粒子群算法?2 举个例子3 还是一个例子算法流程算法实现建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 什么是粒子群算法? 粒子群算法(Pa…...

Tomcat 集群介绍
一.Tomcat 集群介绍 在实际生产环境中,单台 Tomcat 服务器的负载能力或者说并发能力在四五百左右。大 部分情况下随着业务增长,访问量的增加(并发量不止四五百),单台 Tomcat 服务器是 无法承受的。这时就需要将多台 Tomcat 服务器组织起来&a…...
Windows右键添加用 IDEA 打开
1.安装IDEA时 安装时会有个选项来添加,如下: 勾选即可 2.修改注册表 安装时未勾选,可以把下面代码中程序路径改为自己的,保存为对应的 idea.reg文件,双击即可 Windows Registry Editor Version 5.00[HKEY_CLASSES…...

Golang 中return和defer执行先后顺序
先给出最终结论: 执行return语句 -> 执行defer函数 -> 函数返回 这里可能会有一个疑问, 执行return语句和函数返回难道不是一回事? Golang语言中函数的return不是原子操作,而是分为了两步: 返回值赋值真正函数返回 Gol…...

业务数据模拟/采集
业务数据模拟/采集 2.2 业务数据模拟 2.2.1 连接MySQL 通过MySQL可视化客户端连接数据库。2.2.2 建表语句 1)通过SQLyog创建数据库2)设置数据库名称为gmall,编码为utf-8,排序规则为utf8_general_ci3)导入数据库结构脚本…...
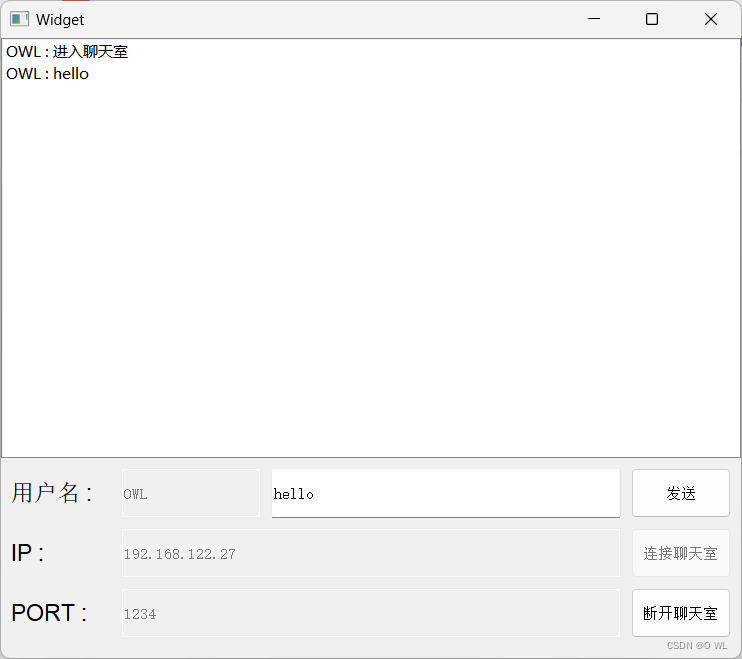
qt day 5
实现局域网的网络聊天室功能 1>服务器代码 --------------------------------------------------------------- widget.h --------------------------------------------------------------- #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMes…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
