QuantLib学习笔记——InterestRate的应用
⭐️ 单利还是复利
巴菲特老爷子有句名言:“人生就像滚雪球,重要的是发现很湿的雪和很长的坡。” 很湿的雪,指的就是复利。很长的坡,指的就是时间。很湿的雪和很长的坡组合起来,就能滚成巨大的雪球。
哈哈,复利是多么让人愉快啊!!!连爱因斯坦都称它为世界第八大奇迹。

这里引出一个概念:计息方式,
大家知道,计息方式有两种,单利和复利,两者的主要区别在于利息是否参与计息,在单利中,每次产生的利息不会和本金放在一起参与计息,而复利则相反。👇
单利:是指按照固定的本金计算利息
复利:是指第一期产生利息后,第二次的本金包括之前的本金和上次产生的利息,以此为本金计算利息,后面的计息周期以此类推(复利又叫利滚利)。
假如你有一项投资,你希望它是单利的,还是复利的?
⭐️ 因子
为说明因子的概念,这里需要引入一些公式,很简单的公式,我们以复利为例。
设P代表终值,r代表利率,U代表本金或初值,n代表计息期数,比如1年,1个月等等。
按照复利的定义,我没有

n可以取整数,也可以取小数,比如以年为计息周期,则n取0.5代表半年。
这里出现了复利因子和折扣因子,我们可以看出,
当前价值一块钱的资产,在计息结束后的价值就等于复利因子。
计息结束后价值一块钱的资产,其当前价值就等于折扣因子。
复利因子和折扣因子是互为倒数的关系。
单利的情况依次类推。
⭐️ QuantLib的利率类
该类用于实例化一个利率(而非利率期限结构)并提供了一些利率相关的计算
ql.InterestRate(rate, dayCount, compounding, frequency)
参数说明如下
| 参数 | 说明 |
|---|---|
| rate | 利率的值 |
| dayCounter | 计日器,它可以按照某种约定判断某日是否参与计息并计算计息天数 |
| compounding | 是单利还是复利计息 |
| frequency | 计息频率,是半年一次还是一年一次,等等 |
它有一些重要的成员方法,如下所示
| 参数 | 说明 |
|---|---|
| rate() | 返回利率的值 |
| dayCounter() | 返回计日器对象 |
| discountFactor(d1, d2) | 计算从日期d1到日期d2这段时间的折扣因子,d1小于d2 |
| compoundFactor(d1, d2) | 计算从日期d1到日期d2这段时间的复利因子或单利因子,d1小于d2 |
| impliedRate(compound, resultDC, comp, freq, d1, d2) | 在给定某段时间内的复利因子的情况下,返回一个利率,这个利率就是隐含利率 |
| equivalentRate(resultDC, comp, freq, d1, d2) | 返回一个等效利率 |
这里特别说明一下 equivalentRate 这个方法,它产生一个和当前利率等效的利率
何为等效?在这里,等效就是经过一段时间的计息,产生了相同的利息。等效利率和原利率可以有不同的日期计数规则,计息方式和计息频率等。
⭐️ 代码
本文代码调用了一些利率类的方法
import QuantLib as qlif __name__ == "__main__": # 当前利率的值r = 0.05# 输出按公式计算的因子print("python计算的两年期复利因子: ", (1+r)**2)print("python计算的两年期折扣因子: ", 1/(1+r)**2) # 开始计息日d1 = ql.Date(15,6,2020)# 结束计息日d2 = ql.Date(15,6,2022)# 利率对象rate = ql.InterestRate(r, ql.Actual360(), ql.Compounded, ql.Annual)# 利率值print("利率值: ", rate.rate())# 日期计数器print("日期计数器: ", rate.dayCounter())# 2年以后,即2年期折扣因子print("2年期折扣因子: ", rate.discountFactor(2))# 从d1到d2的折扣因子print("从d1到d2的折扣因子: ", rate.discountFactor(d1, d2))# 从d1到d2的复利因子print("从d1到d2的复利因子: ", rate.compoundFactor(d1, d2))# 等效利率print("等效利率: ", rate.equivalentRate(ql.Actual360(), ql.Compounded, ql.Semiannual, d1, d2))# 隐含利率factor = rate.compoundFactor(d1, d2)print("隐含利率: ", rate.impliedRate(factor, ql.Actual360(), ql.Continuous, ql.Annual, d1, d2))代码执行结果如下
python计算的两年期复利因子: 1.1025
python计算的两年期折扣因子: 0.9070294784580498
利率值: 0.05
日期计数器: Actual/360 day counter
2年期折扣因子: 0.9070294784580498
从d1到d2的折扣因子: 0.9058010300610555
从d1到d2的复利因子: 1.103995211765872
等效利率: 4.939015 % Actual/360 Semiannual compounding
隐含利率: 4.879016 % Actual/360 continuous compounding
笔者水平有限,若有不对的地方欢迎评论指正!
相关文章:

QuantLib学习笔记——InterestRate的应用
⭐️ 单利还是复利 巴菲特老爷子有句名言:“人生就像滚雪球,重要的是发现很湿的雪和很长的坡。” 很湿的雪,指的就是复利。很长的坡,指的就是时间。很湿的雪和很长的坡组合起来,就能滚成巨大的雪球。 哈哈࿰…...

记录--解决前端内存泄漏:问题概览与实用解决方案
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 内存泄漏是前端开发中的一个常见问题,可能导致项目变得缓慢、不稳定甚至崩溃。在本文中,我们将深入探讨在JavaScript、Vue和React项目中可能导致内存泄漏的情况,并提…...
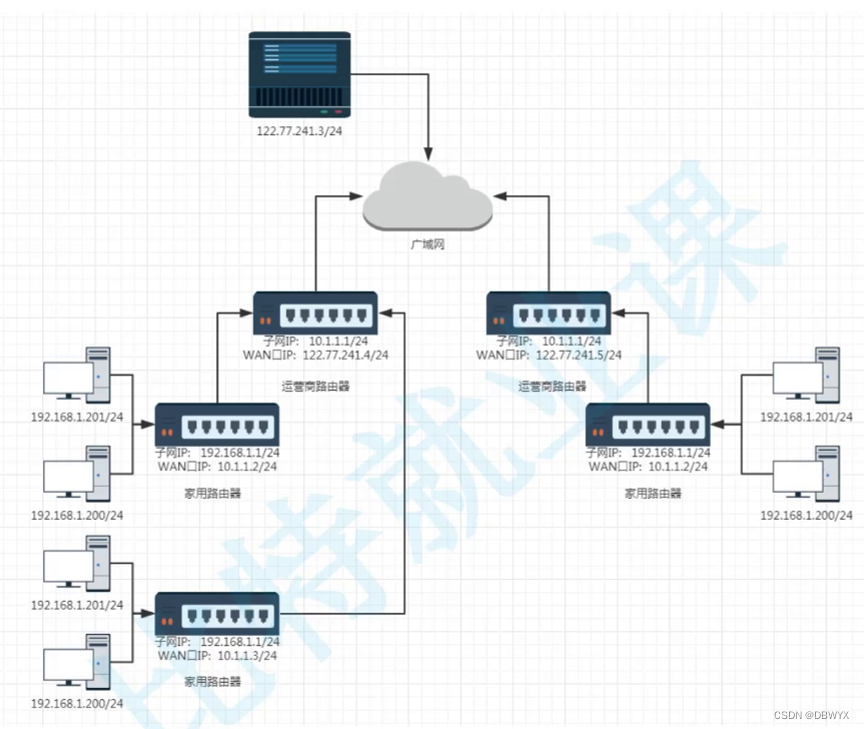
IP初学习
1.IP报文 首部长度指的是报头长度,用于分离报头和有效载荷 2.网段划分 IP地址 目标网络 目标主机 3.例子 4.特殊的IP地址 5.真正的网络环境 6.调制解调器 “猫”,学名叫宽带无线猫 7.NAT 源IP在内网环境不断被替换 8.私有IP不能出现在公网上 因…...

live5555 testProgs目录
文章目录 测试testProgs视频流直播流注意: 测试 testProgs 当涉及到许多示例程序时,解释每一个都可能会变得非常冗长。然而,我可以为你提供一些关键示例程序的简要解释,以帮助你了解每个示例的用途和功能: testOnDem…...

yolov5模型s,l,m,x的区别
yolov5s 是什么?yolov5系列最小的模型,s是small。 适合什么情况下使用?适合在计算资源有限的设备上使用。如移动设备或边缘设备。 速度和准确率:速度最快,准确率最低。 输入分辨率:通常为640x640 # Param…...

Springboot 实践(13)spring boot 整合RabbitMq
前文讲解了RabbitMQ的下载和安装,此文讲解springboot整合RabbitMq实现消息的发送和消费。 1、创建web project项目,名称为“SpringbootAction-RabbitMQ” 2、修改pom.xml文件,添加amqp使用jar包 <!-- RabbitMQ --> <dependency&g…...
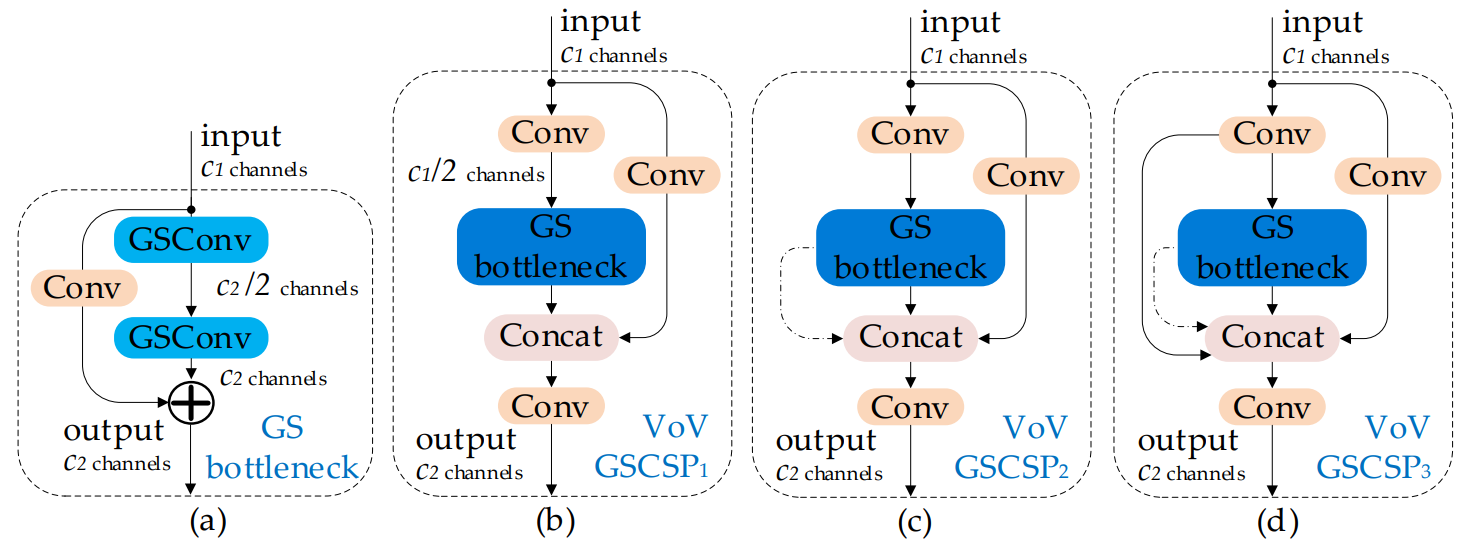
YoloV8改进策略:轻量级Slim Neck打造极致的YoloV8
文章目录 摘要Yolov8官方结果源码改进方法测试结果总结摘要 论文链接:https://arxiv.org/ftp/arxiv/papers/2206/2206.02424.pdf 作者研究了增强 CNN 学习能力的通用方法,例如 DensNet、VoVNet 和 CSPNet,然后根据这些方法的理论设计了 Slim-Neck 结构。 使用轻量级卷积…...
使用java代码给Excel加水印,代码全,进阶版
以下代码,亲测可以跑通 1、上一篇博客用了Apache POI库3.8的版本的形式对Excel加了水印,但是最近主线版本用了4.1.2的形式,由于为了保持版本的兼容性,下面有开发了Apache POI的4.1.2的版本号的方案。 pom文件为: <d…...

day37:网编day4,多点通信和并发服务器
一、广播接收方: #include <myhead.h>#define ERR_MSG(msg) do{\ fprintf(stderr,"__%d__\n",__LINE__);\ perror(msg);\ }while(0)#define BRD_IP "192.168.114.255" #define BRD_PORT 8888int main(int argc, const char *argv[]) {//…...
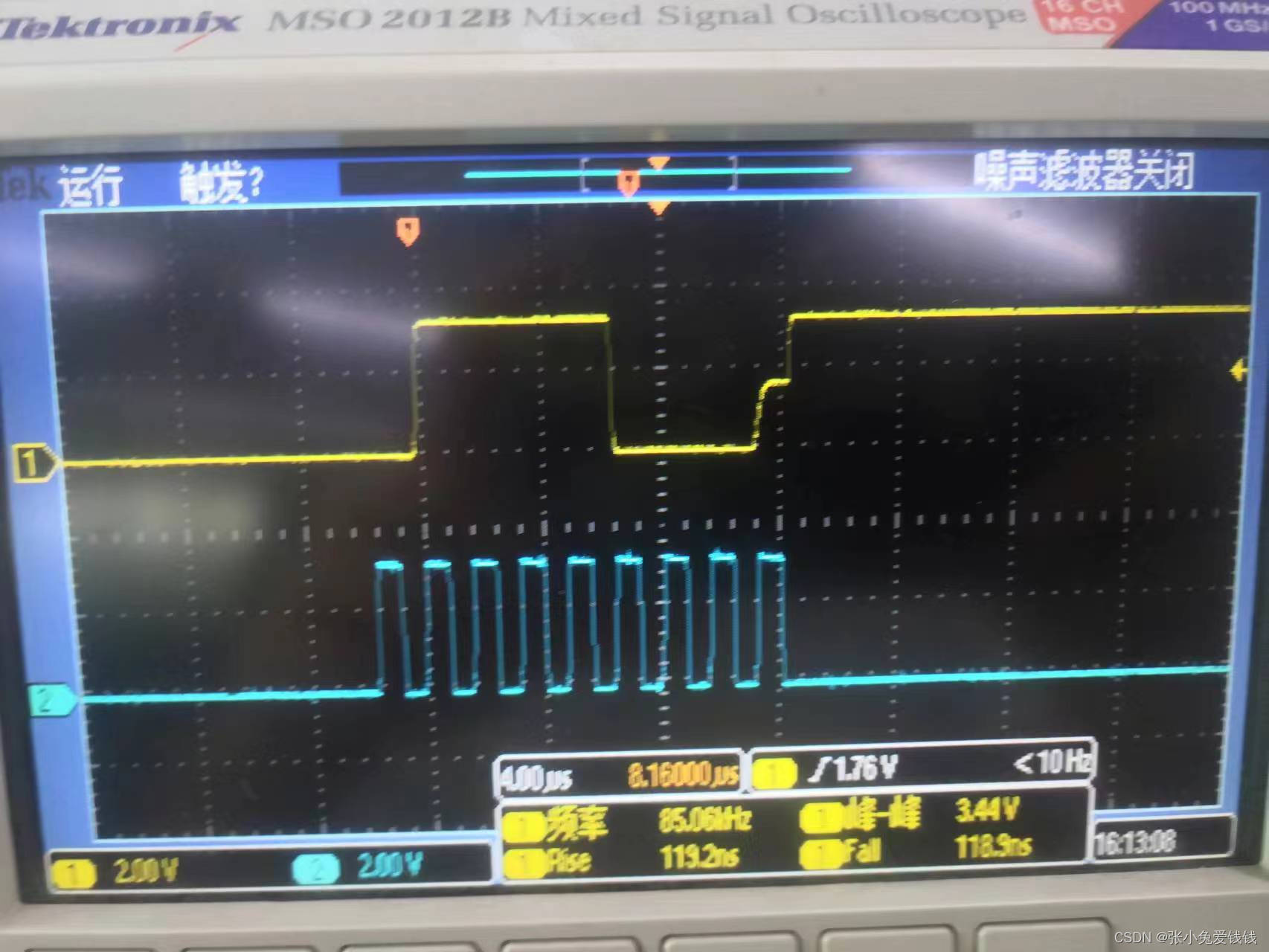
STM32 硬件IIC 控制OLED I2C卡死问题
1. STM32L151C8T6 硬件IIC 控制OLED 屏,OLED 驱动IC CH1116G, 查阅OLED 数据手册 2. STM32 硬件IIC 初始化,用的标准库,固件库 // stm32l151c8t6 as master, oled control ic (CH1116G) as slave, and communicate by master iic2 void STM3…...

Redis图文指南
1、什么是 Redis? Redis(REmote DIctionary Service)是一个开源的键值对数据库服务器。 Redis 更准确的描述是一个数据结构服务器。Redis 的这种特殊性质让它在开发人员中很受欢迎。 Redis不是通过迭代或者排序方式处理数据,而是…...

C++17 std::string_view介绍与使用
std::string_view介绍 std::string_view是C17增加的新内容。它是一个轻量级的、只读的字符串视图,可以用来表示一个字符串或字符串的一部分。std::string_view可以提高代码的可读性、可维护性和性能。 std::string_view与std::string的主要区别在于,st…...
写得了代码,焊得了板!嵌入式开发工程师必修之代码管理方案(下)
目录 极狐GitLab嵌入式开发场景解决方案 3.1 高可用部署与灾备 3.2 组织管理 3.3 分支策略 3.4 分支保护 3.5 推送规则 3.6 代码评审 3.7 数据保护 3.8 其他相关 本文来自 武让 极狐GitLab 高级解决方案架构师 💡 前两篇文章,作者介绍了嵌入式开…...
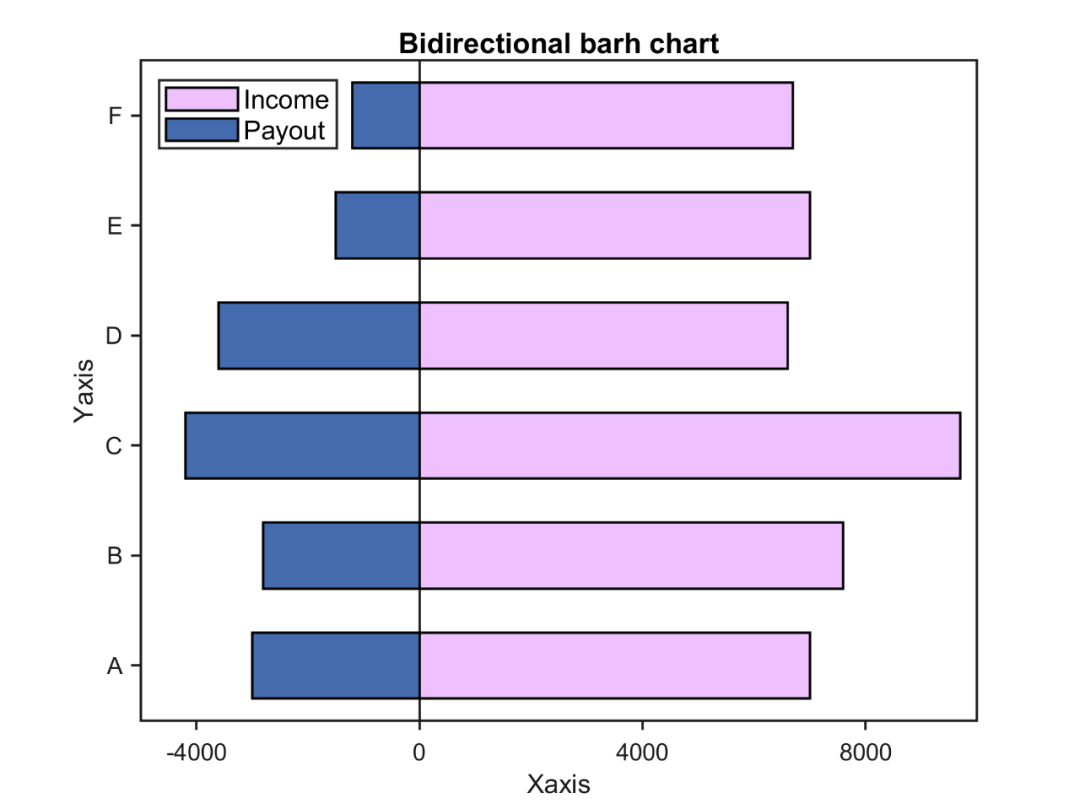
Matlab论文插图绘制模板第110期—水平双向柱状图
在之前的文章中,分享了很多Matlab柱状图的绘制模板: 进一步,再来看一种特殊的柱状图:水平双向柱状图。 先来看一下成品效果: 特别提示:本期内容『数据代码』已上传资源群中,加群的朋友请自行下…...

【广州华锐互动】VR全景工厂虚拟导览,虚拟现实技术提升企业数字化信息管理水平
随着工业4.0的到来,VR工厂全景制作成为了越来越多工业企业的选择。传统的工厂管理方式往往存在诸多问题,如信息不对称、安全隐患等。为了解决这些问题,VR工厂全景制作应运而生,它通过结合虚拟现实现实技术和数据采集技术ÿ…...
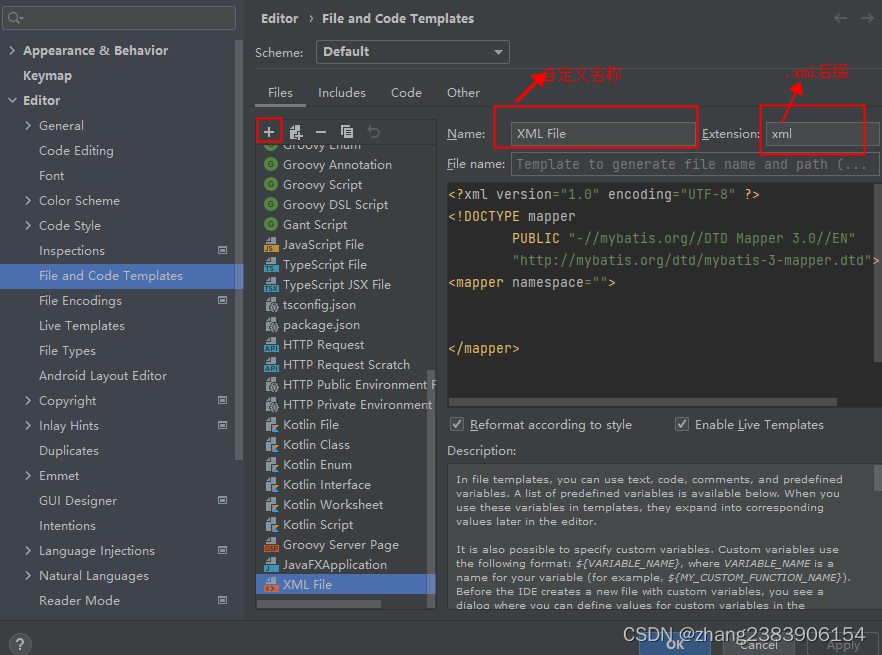
idea 创建mybatis xml文件时找不到
1、File >Settings 如图 : 2、添加模板:如下图 3、添加xml模板 如下图: 模板内容: <?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE mapperPUBLIC "-//mybatis.org//DTD Mapper 3.0//E…...

Python钢筋混凝土结构计算.pdf-混凝土构件计算
计算原理: 代码实现: #钢筋混凝土参数 def c_hrb(): global fcuk,HRB,Ec,fc,ft,ftk,Es,fy,fyp,fyk global a1,epsilon_cu fcukEcfcftftk0.0 HRBEsfyfypfyk0.0 #矩形应力图系数a1,C50以下为1.0 a11.0 #正截面混凝土极限压应变epsilon_cu&#…...

mysql5.7-基于docker-compose搭建主从同步
一、环境信息 系统版本:CentOS Linux release 7.9.2009 (Core) cat /etc/centos-release Docker版本:Docker version 20.10.6, build 370c289 docker --version Docker-compose版本:Docker Compose version v2.10.2 docker-compose --versio…...
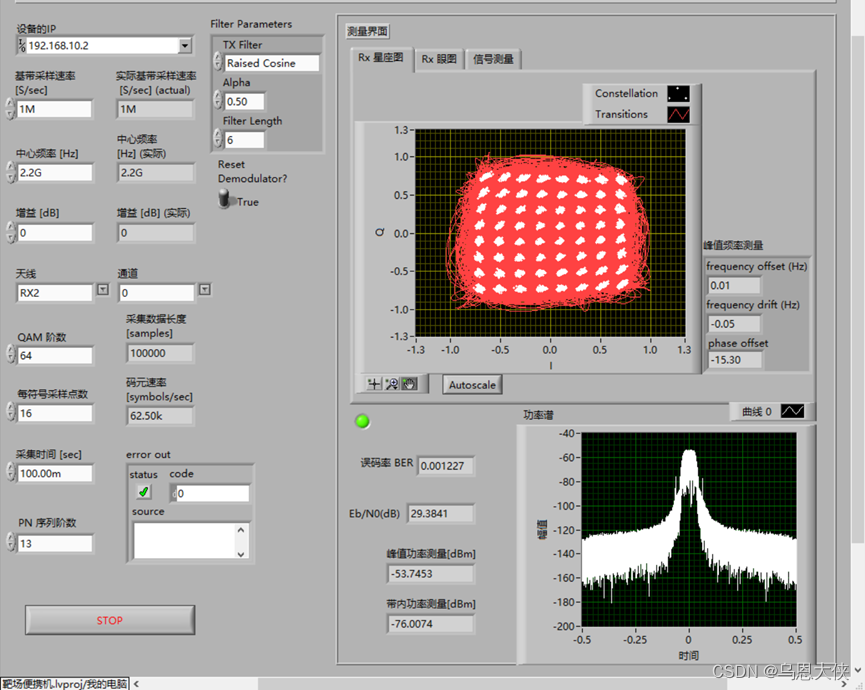
【USRP】调制解调系列5:16QAM、32QAM、64QAM、256QAM、1024QAM、基于labview的实现
QAM 正交振幅键控是一种将两种调幅信号(2ASK和2PSK)汇合到一个信道的方法,因此会双倍扩展有效带宽,正交调幅被用于脉冲调幅。正交调幅信号有两个相同频率的载波,但是相位相差90度(四分之一周期,…...
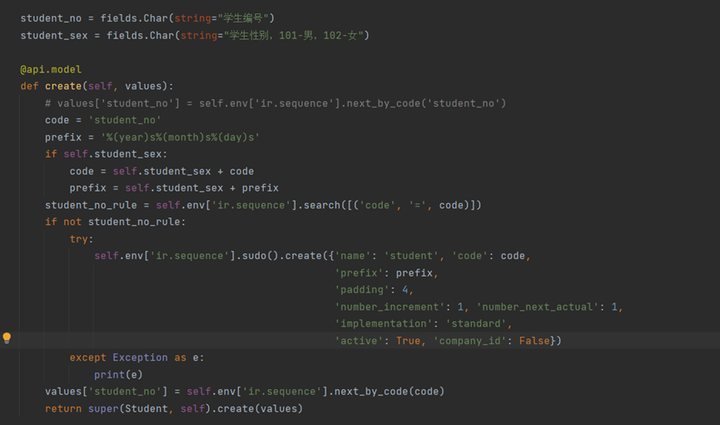
Odoo|5分钟创建自定义的业务系统唯一序列号
在业务操作中,经常会遇到需要生成全局唯一序列号数据的情况,比如订单号、报价单号等。为了确保数据的唯一性和准确性,通常我们会使用Redis或其他分布式锁机制来实现。然而,很多人可能不知道,odoo框架本身提供了一个原生…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...
