C++17 std::string_view介绍与使用
std::string_view介绍
std::string_view是C++17增加的新内容。它是一个轻量级的、只读的字符串视图,可以用来表示一个字符串或字符串的一部分。std::string_view可以提高代码的可读性、可维护性和性能。
std::string_view与std::string的主要区别在于,std::string_view只读,而std::string可读可写。这意味着std::string_view不必担心对字符串的修改,从而可以提高性能。此外,std::string_view可以用来表示字符串的一部分,而std::string只能表示整个字符串。这使得std::string_view可以更加灵活地使用。
std::string_view使用
std::string_view的使用方法如下:
std::string_view s("Hello, world!");// s is a read-only view of the string "Hello, world!"std::cout << s << std::endl; // Prints "Hello, world!"// s can be used to iterate over the stringfor (auto c : s) {std::cout << c;
} // Prints "Hello, world!"// s can be used to compare to other stringsif (s == "Hello, world!") {std::cout << "The strings are equal." << std::endl;
}std::string_view是一个强大的工具,可以用来提高C++代码的可读性、可维护性和性能。
相关文章:

C++17 std::string_view介绍与使用
std::string_view介绍 std::string_view是C17增加的新内容。它是一个轻量级的、只读的字符串视图,可以用来表示一个字符串或字符串的一部分。std::string_view可以提高代码的可读性、可维护性和性能。 std::string_view与std::string的主要区别在于,st…...
写得了代码,焊得了板!嵌入式开发工程师必修之代码管理方案(下)
目录 极狐GitLab嵌入式开发场景解决方案 3.1 高可用部署与灾备 3.2 组织管理 3.3 分支策略 3.4 分支保护 3.5 推送规则 3.6 代码评审 3.7 数据保护 3.8 其他相关 本文来自 武让 极狐GitLab 高级解决方案架构师 💡 前两篇文章,作者介绍了嵌入式开…...
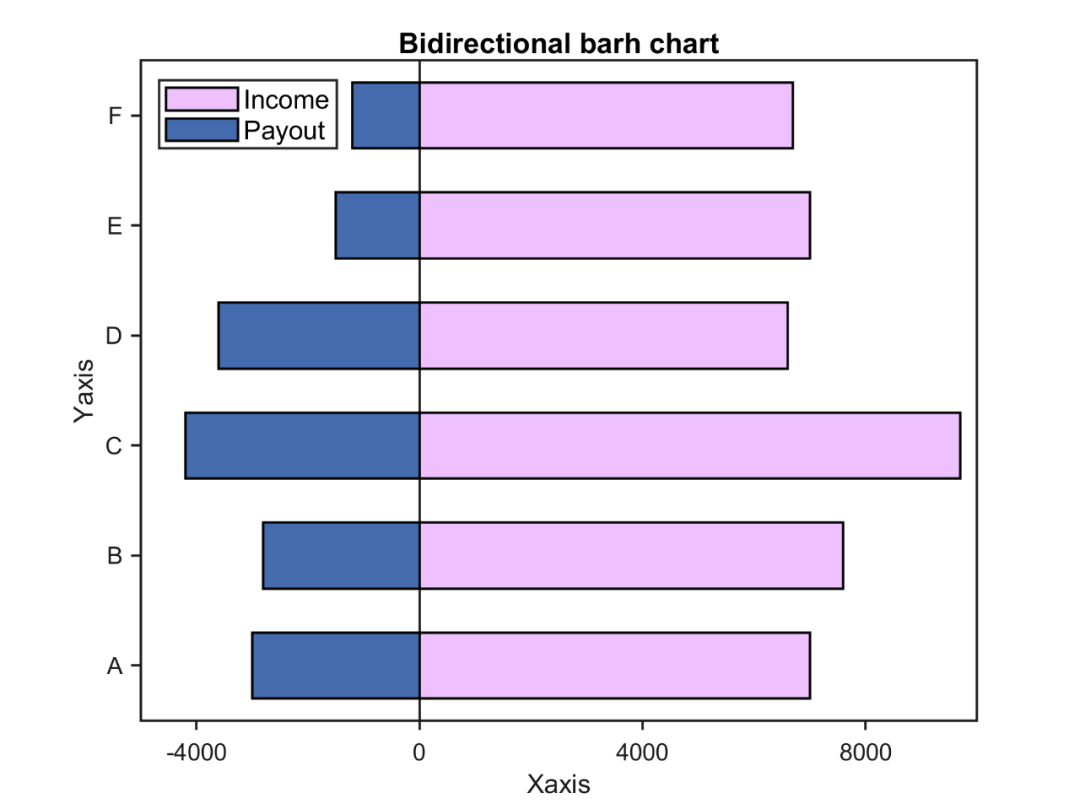
Matlab论文插图绘制模板第110期—水平双向柱状图
在之前的文章中,分享了很多Matlab柱状图的绘制模板: 进一步,再来看一种特殊的柱状图:水平双向柱状图。 先来看一下成品效果: 特别提示:本期内容『数据代码』已上传资源群中,加群的朋友请自行下…...

【广州华锐互动】VR全景工厂虚拟导览,虚拟现实技术提升企业数字化信息管理水平
随着工业4.0的到来,VR工厂全景制作成为了越来越多工业企业的选择。传统的工厂管理方式往往存在诸多问题,如信息不对称、安全隐患等。为了解决这些问题,VR工厂全景制作应运而生,它通过结合虚拟现实现实技术和数据采集技术ÿ…...
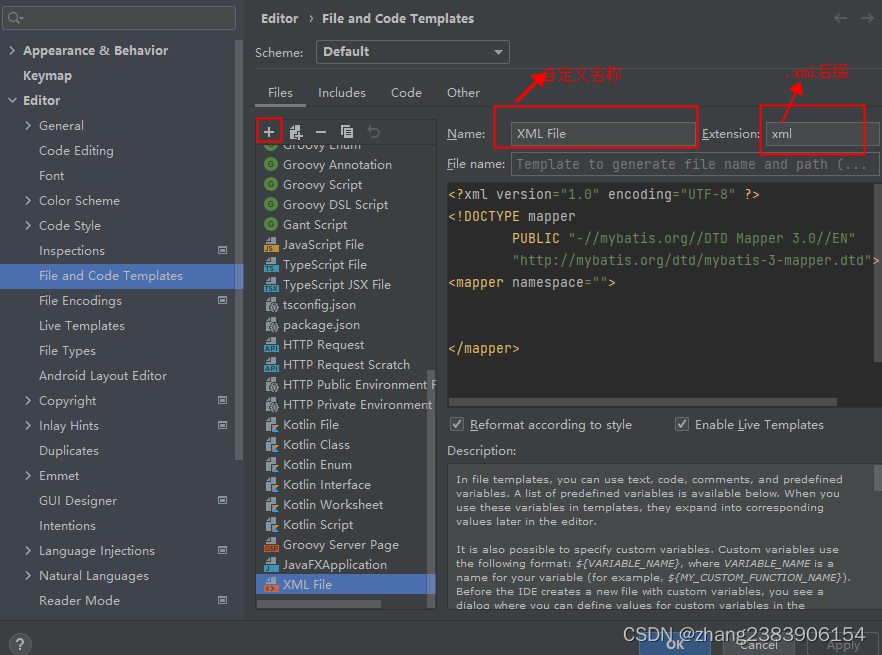
idea 创建mybatis xml文件时找不到
1、File >Settings 如图 : 2、添加模板:如下图 3、添加xml模板 如下图: 模板内容: <?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE mapperPUBLIC "-//mybatis.org//DTD Mapper 3.0//E…...

Python钢筋混凝土结构计算.pdf-混凝土构件计算
计算原理: 代码实现: #钢筋混凝土参数 def c_hrb(): global fcuk,HRB,Ec,fc,ft,ftk,Es,fy,fyp,fyk global a1,epsilon_cu fcukEcfcftftk0.0 HRBEsfyfypfyk0.0 #矩形应力图系数a1,C50以下为1.0 a11.0 #正截面混凝土极限压应变epsilon_cu&#…...

mysql5.7-基于docker-compose搭建主从同步
一、环境信息 系统版本:CentOS Linux release 7.9.2009 (Core) cat /etc/centos-release Docker版本:Docker version 20.10.6, build 370c289 docker --version Docker-compose版本:Docker Compose version v2.10.2 docker-compose --versio…...
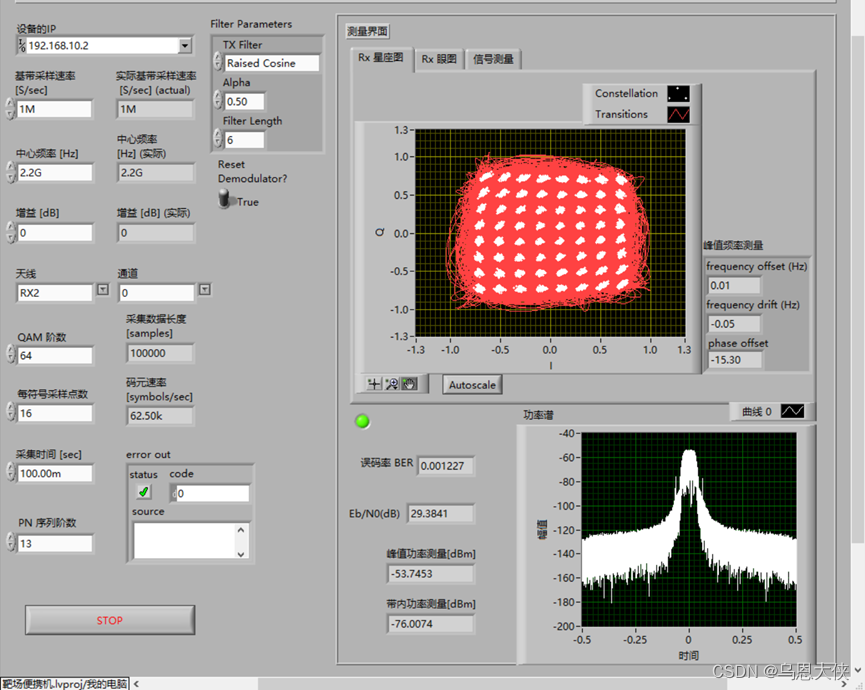
【USRP】调制解调系列5:16QAM、32QAM、64QAM、256QAM、1024QAM、基于labview的实现
QAM 正交振幅键控是一种将两种调幅信号(2ASK和2PSK)汇合到一个信道的方法,因此会双倍扩展有效带宽,正交调幅被用于脉冲调幅。正交调幅信号有两个相同频率的载波,但是相位相差90度(四分之一周期,…...
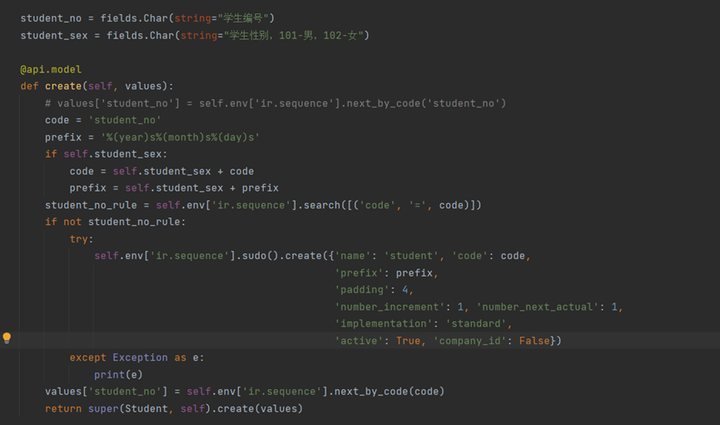
Odoo|5分钟创建自定义的业务系统唯一序列号
在业务操作中,经常会遇到需要生成全局唯一序列号数据的情况,比如订单号、报价单号等。为了确保数据的唯一性和准确性,通常我们会使用Redis或其他分布式锁机制来实现。然而,很多人可能不知道,odoo框架本身提供了一个原生…...
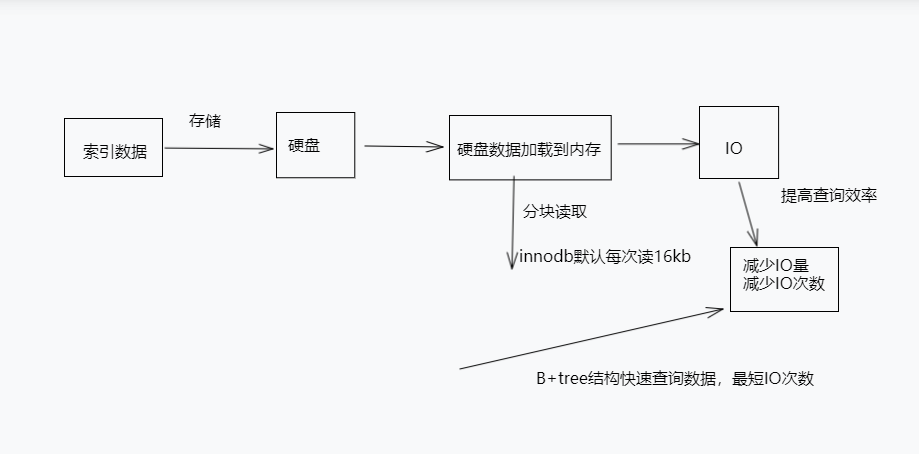
mysql索引为什么提高查询速度(底层原理)
一、索引原理图 二、索引数据存储到硬盘而不是内存? 硬盘内存 成本低成本高 容量大容量小 读写速度一般读取速度快 断电后数据永久存储断电后数据清空 三、硬盘数据为什么要读取到内存?为啥不直接…...

算法通关村——位运算在查找重复元素中的妙用
用4KB内存寻找重复元素 给定一个数组,包含从1到N的整数,N最大为32000,数组可能还有重复值,且N的取值不定,若只有4KB的内存可用,该如何打印数组中所有重复元素。 如果不要求使用4KB,最简单就是…...
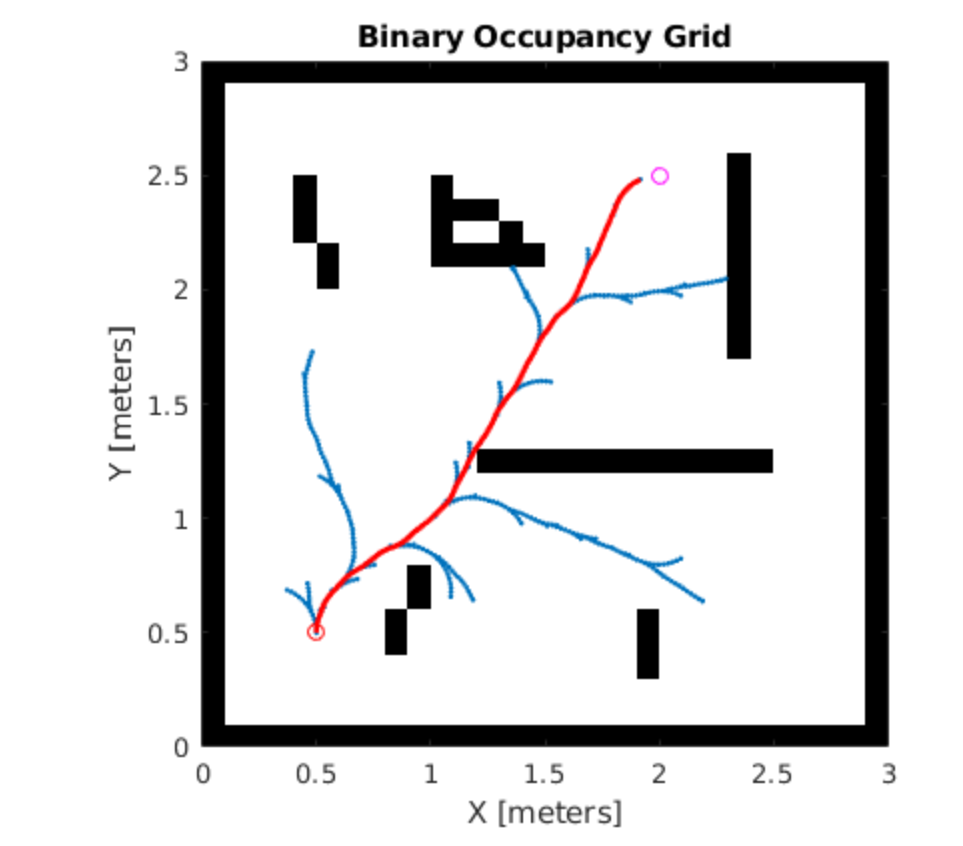
使用环境中的视觉地标和扩展卡尔曼滤波器定位移动机器人研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【python基础知识】5.for循环和while循环
文章目录 前言for...in...循环语句for循环:空房间for循环:一群排队办业务的人range()函数for循环:办事流程 while循环while循环:放行条件while循环:办事流程 两种循环对比 前言 上一关,我们学习了两种新的…...
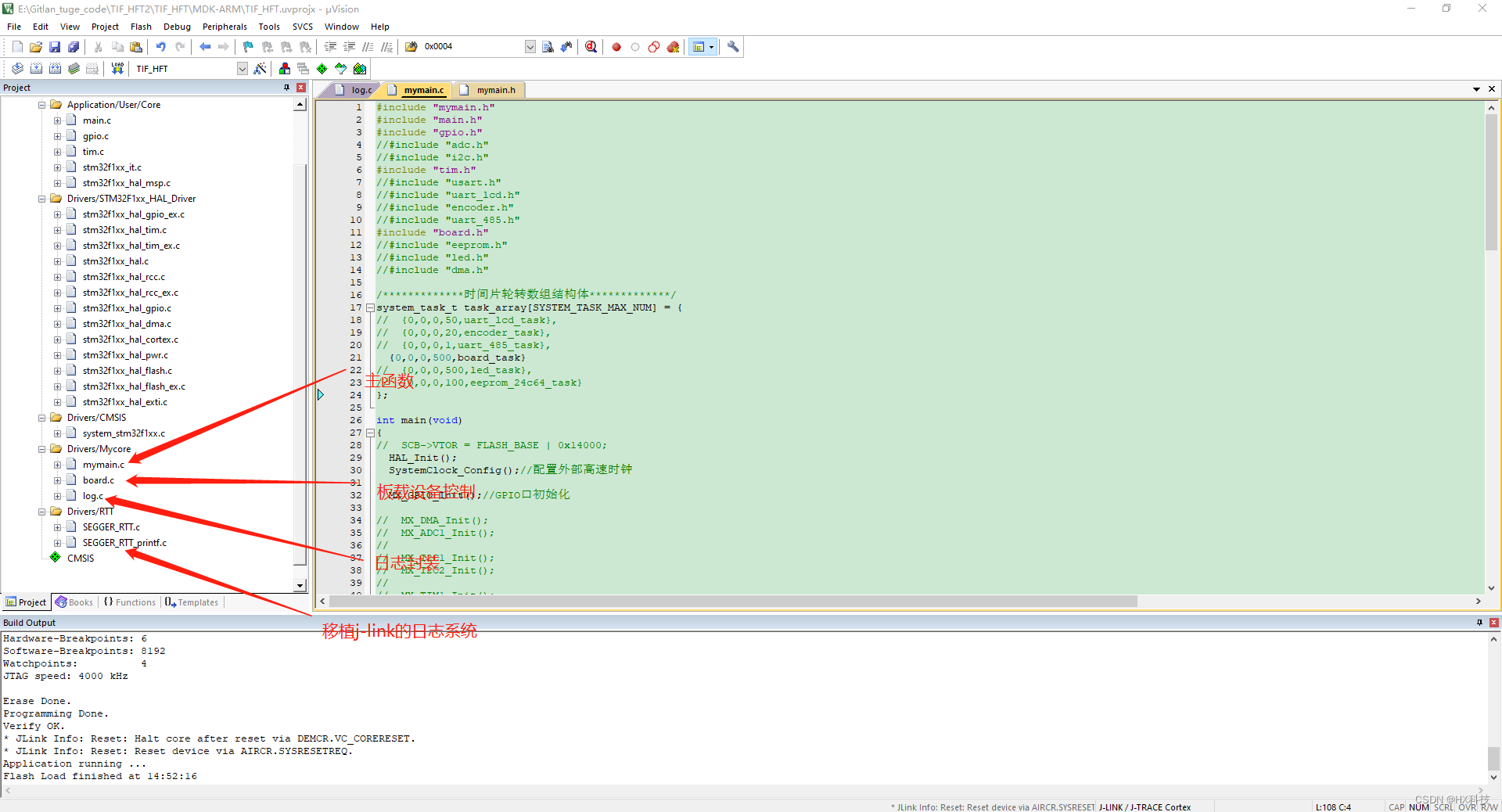
STM32CUBEMX_创建时间片轮询架构的软件框架
STM32CUBEMX_创建时间片轮询架构的软件框架 说明: 1、这种架构避免在更新STM32CUBEMX配置后把用户代码清除掉 2、利用这种时间片的架构可以使得代码架构清晰易于维护 创建步骤: 1、使用STM32CUBEMX创建基础工程 2、新建用户代码目录 3、构建基础的代码框…...

vue 插槽Slots
vue插槽官网 <button class"fancy-btn"><slot></slot> <!-- 插槽出口 --> </button><slot> 元素是一个插槽出口 (slot outlet),标示了父元素提供的插槽内容 (slot content) 将在哪里被渲染。 // 定义一个Child.vue…...

论文阅读《Nougat:Neural Optical Understanding for Academic Documents》
摘要 科学知识主要存储在书籍和科学期刊中,通常以PDF的形式。然而PDF格式会导致语义信息的损失,特别是对于数学表达式。我们提出了Nougat,这是一种视觉transformer模型,它执行OCR任务,用于将科学文档处理成标记语言&a…...

较难的换根dp:P6213 「SWTR-04」Collecting Coins
传送门 前题提要:感觉这道换根dp可以说是集中了换根dp的所有较高难度的操作和思想,以及较高的一些实现细节,可以说能够完全写出这道题才叫真正理解了换根dp,非常值得一做. 首先读完题意,不难发现这道题有很多限制.点的访问次数限制,必须访问某一个点,想要获得最大的贡献,没有…...

Springboot - 15.二级分布式缓存集成-Caffeine
👀中文文档 Caffeine 👀使用Caffeine (本地缓存) 当与Spring Boot结合使用时,Caffeine提供了一个直观且功能强大的二级缓存解决方案。Spring Boot的缓存抽象使得整合Caffeine变得相当简单。以下是如何在Spring Boot…...
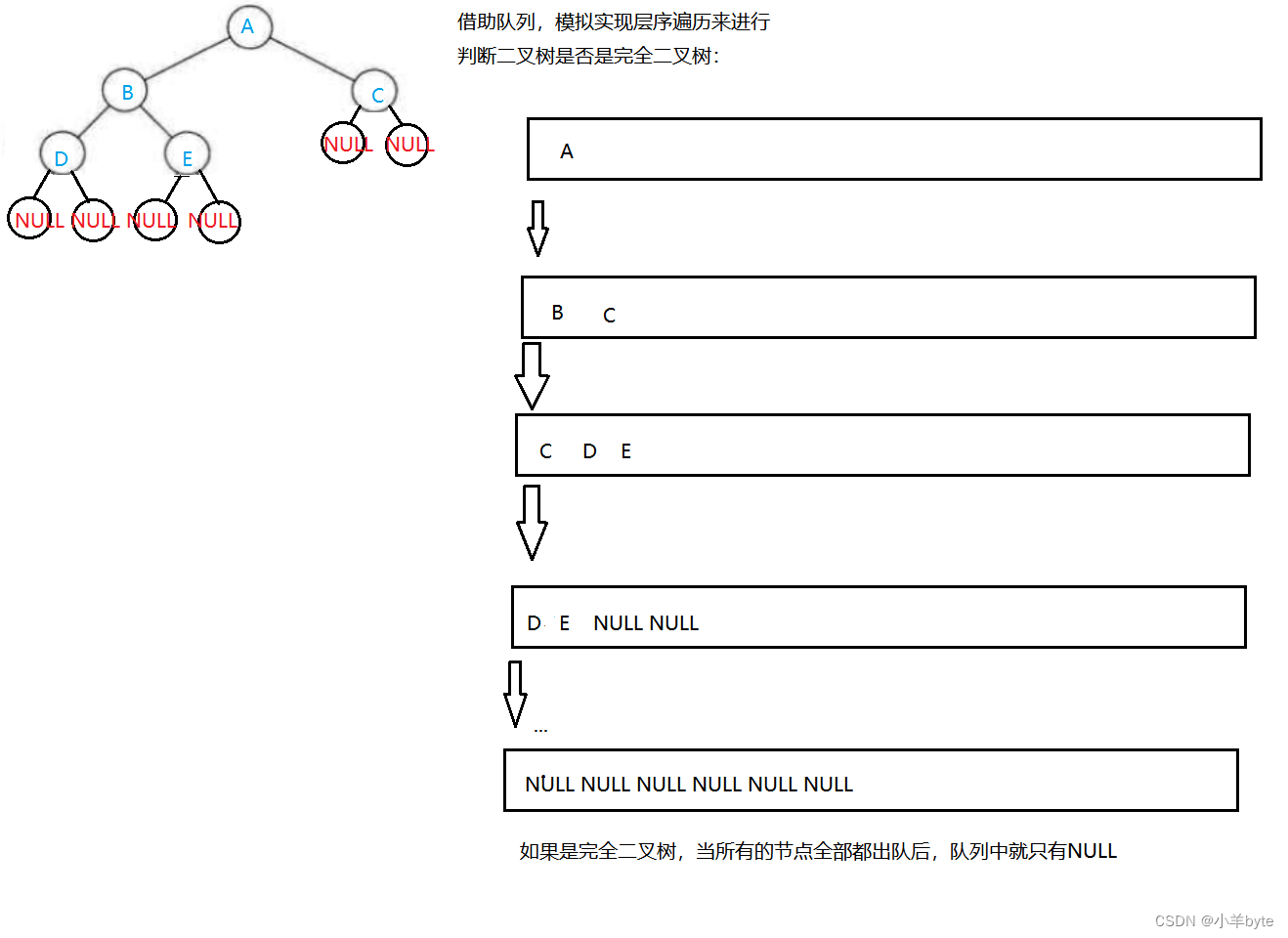
二叉树的介绍及二叉树的链式结构的实现(C语言版)
前言 二叉树是一种特殊的树,它最大的度为2,每个节点至多只有两个子树。它是一种基础的数据结构,后面很多重要的数据结构都是依靠它来进行实现的。了解并且掌握它是很重要的。 目录 1.二叉树的介绍 1.1概念 1.2现实中的二叉树 1.3特殊的二叉…...
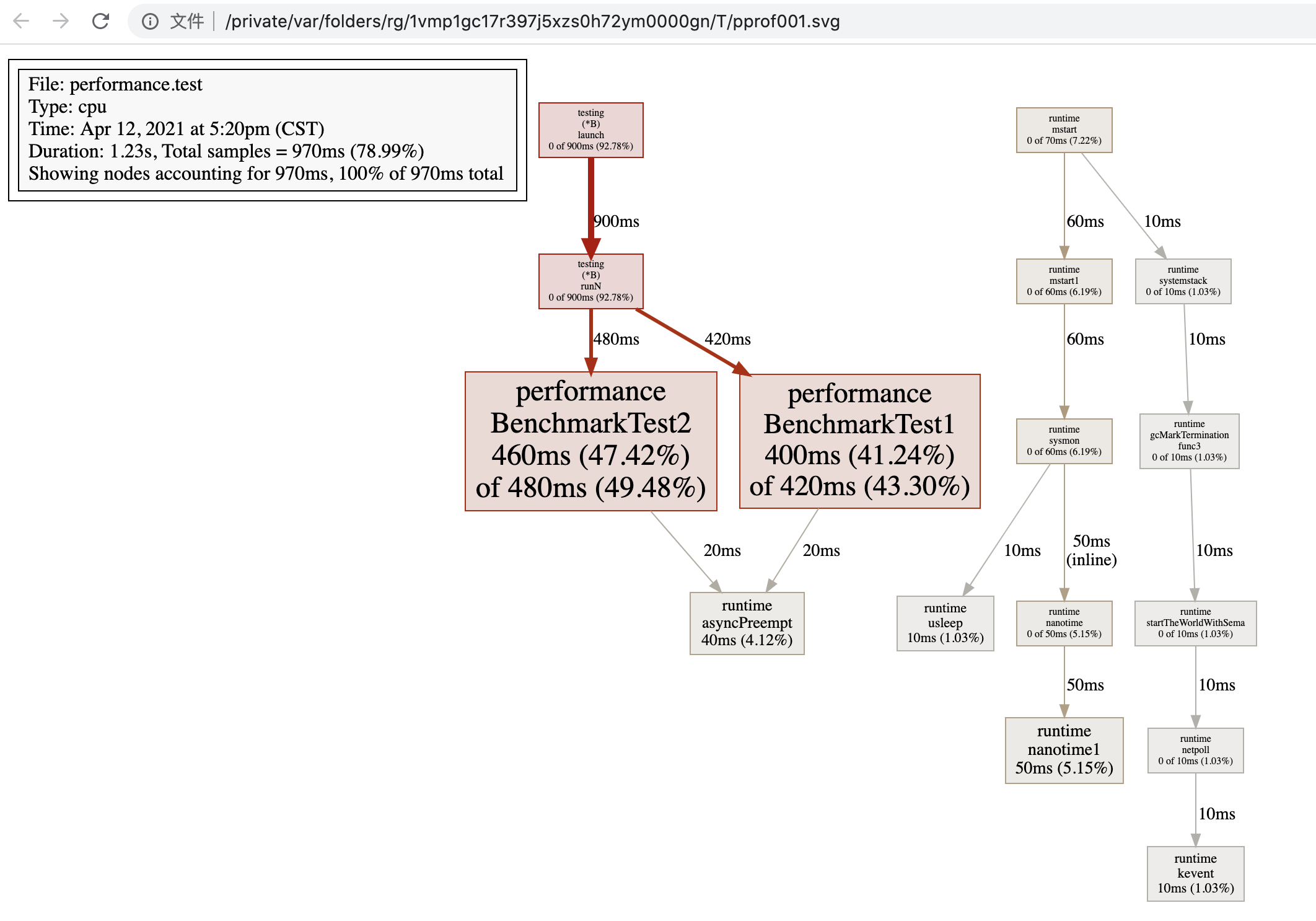
不同写法的性能差异
“ 达到相同目的,可以有多种写法,每种写法有性能、可读性方面的区别,本文旨在探讨不同写法之间的性能差异 len(str) vs str "" 本部分参考自: [问个 Go 问题,字符串 len 0 和 字符串 "" ,有啥区别?](https://segmentf…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...
