算法通关村——位运算在查找重复元素中的妙用
用4KB内存寻找重复元素
给定一个数组,包含从1到N的整数,N最大为32000,数组可能还有重复值,且N的取值不定,若只有4KB的内存可用,该如何打印数组中所有重复元素。
如果不要求使用4KB,最简单就是使用N长的数组然后将元素都存入数组,再打印,但是题目规定了4KB,很显然这种做法就不大行了,一定会超出时间限制。
4KB=4 * 8 * 2 ^ 10 比特,这个值是大于32000,可以使用比特数组来存储相应的元素。利用这个位向量,就可以遍历访问整个数组。如果发现数组元素是v,那么就将位置为v的设置为1,碰到重复元素,就输出。代码就没什么可说的,真要实现起来,还是有一点复杂的。
public class FindDuplicatesIn32000 {public void checkDuplicates(int[] array) {BitSet bs = new BitSet(32000);for (int i = 0; i < array.length; i++) {int num = array[i];int num0 = num - 1;if (bs.get(num0)) {System.out.println(num);} else {bs.set(num0);}}}class BitSet {int[] bitset;public BitSet(int size) {this.bitset = new int[size >> 5];}boolean get(int pos) {int wordNumber = (pos >> 5);//除以32int bitNumber = (pos & 0x1F);//除以32return (bitset[wordNumber] & (1 << bitNumber)) != 0;}void set(int pos) {int wordNumber = (pos >> 5);//除以32int bitNumber = (pos & 0x1F);//除以32bitset[wordNumber] |= 1 << bitNumber;}}
}
相关文章:

算法通关村——位运算在查找重复元素中的妙用
用4KB内存寻找重复元素 给定一个数组,包含从1到N的整数,N最大为32000,数组可能还有重复值,且N的取值不定,若只有4KB的内存可用,该如何打印数组中所有重复元素。 如果不要求使用4KB,最简单就是…...
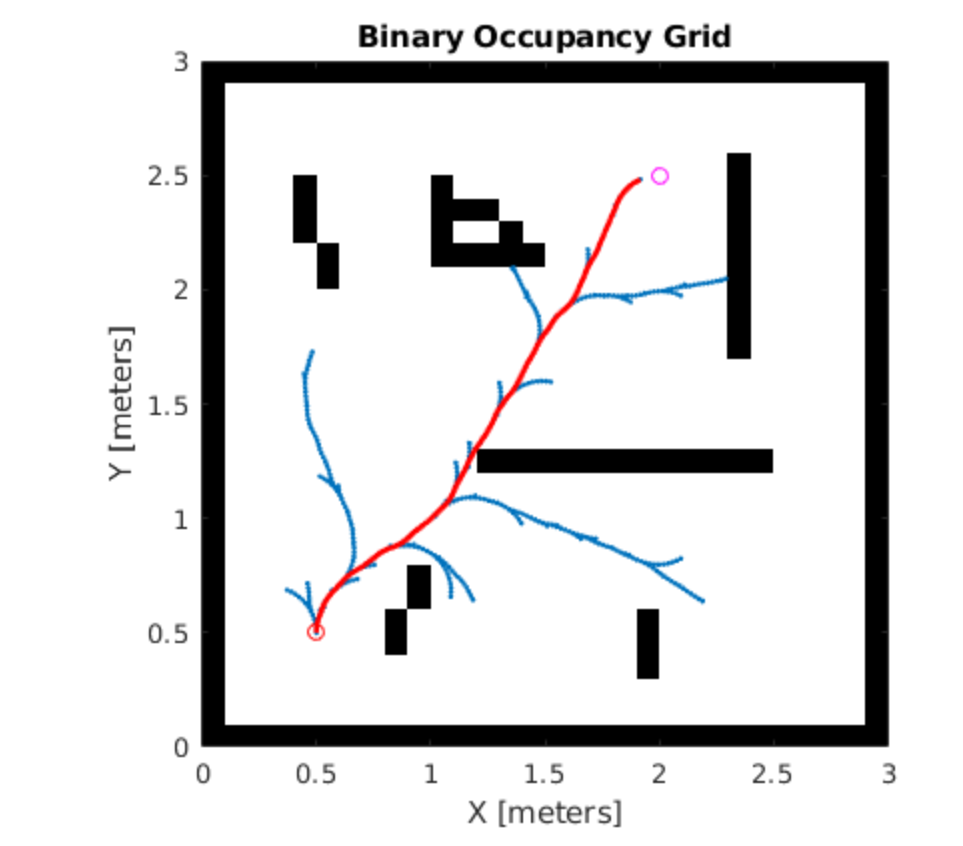
使用环境中的视觉地标和扩展卡尔曼滤波器定位移动机器人研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【python基础知识】5.for循环和while循环
文章目录 前言for...in...循环语句for循环:空房间for循环:一群排队办业务的人range()函数for循环:办事流程 while循环while循环:放行条件while循环:办事流程 两种循环对比 前言 上一关,我们学习了两种新的…...
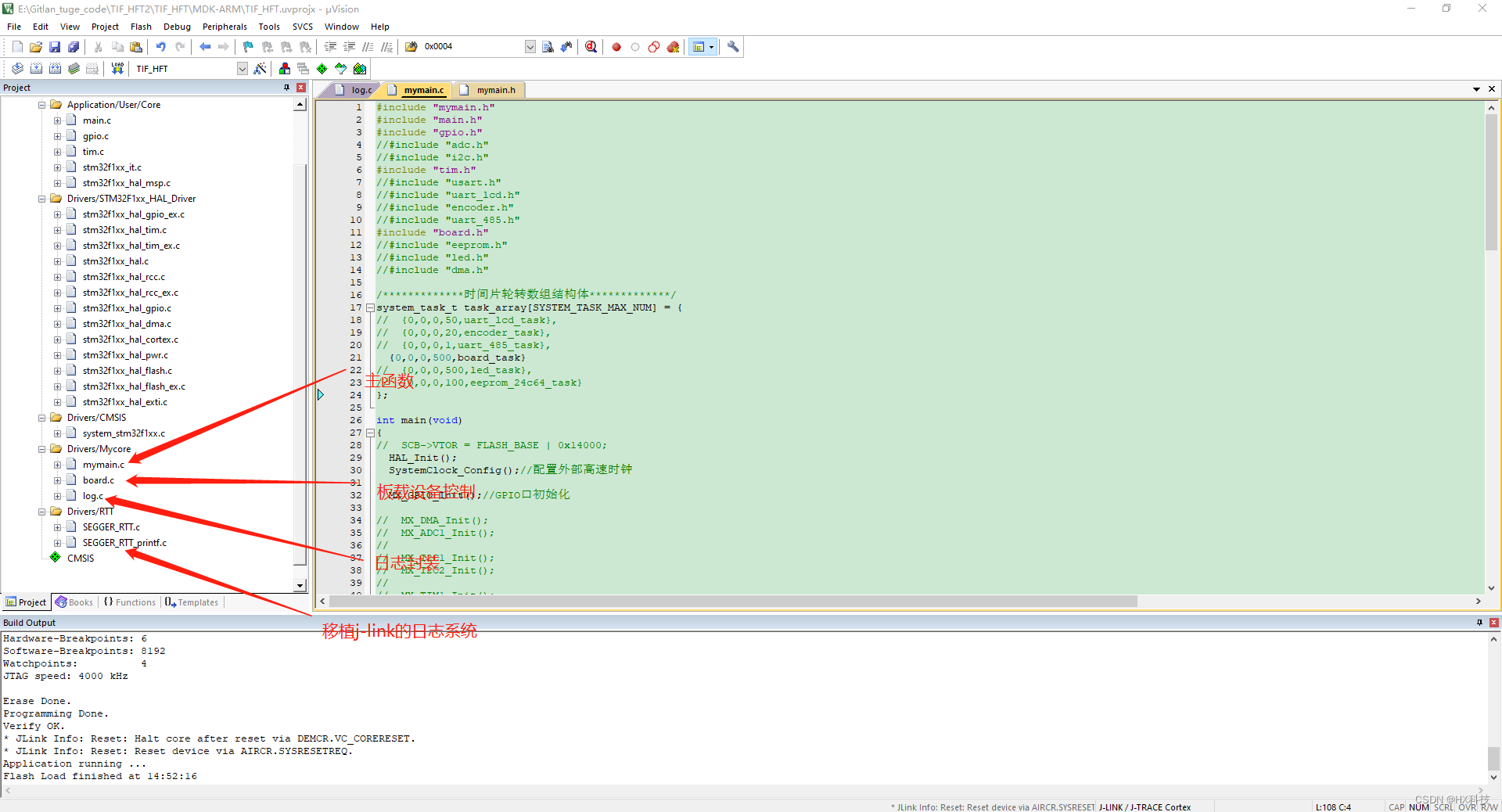
STM32CUBEMX_创建时间片轮询架构的软件框架
STM32CUBEMX_创建时间片轮询架构的软件框架 说明: 1、这种架构避免在更新STM32CUBEMX配置后把用户代码清除掉 2、利用这种时间片的架构可以使得代码架构清晰易于维护 创建步骤: 1、使用STM32CUBEMX创建基础工程 2、新建用户代码目录 3、构建基础的代码框…...

vue 插槽Slots
vue插槽官网 <button class"fancy-btn"><slot></slot> <!-- 插槽出口 --> </button><slot> 元素是一个插槽出口 (slot outlet),标示了父元素提供的插槽内容 (slot content) 将在哪里被渲染。 // 定义一个Child.vue…...

论文阅读《Nougat:Neural Optical Understanding for Academic Documents》
摘要 科学知识主要存储在书籍和科学期刊中,通常以PDF的形式。然而PDF格式会导致语义信息的损失,特别是对于数学表达式。我们提出了Nougat,这是一种视觉transformer模型,它执行OCR任务,用于将科学文档处理成标记语言&a…...

较难的换根dp:P6213 「SWTR-04」Collecting Coins
传送门 前题提要:感觉这道换根dp可以说是集中了换根dp的所有较高难度的操作和思想,以及较高的一些实现细节,可以说能够完全写出这道题才叫真正理解了换根dp,非常值得一做. 首先读完题意,不难发现这道题有很多限制.点的访问次数限制,必须访问某一个点,想要获得最大的贡献,没有…...

Springboot - 15.二级分布式缓存集成-Caffeine
👀中文文档 Caffeine 👀使用Caffeine (本地缓存) 当与Spring Boot结合使用时,Caffeine提供了一个直观且功能强大的二级缓存解决方案。Spring Boot的缓存抽象使得整合Caffeine变得相当简单。以下是如何在Spring Boot…...
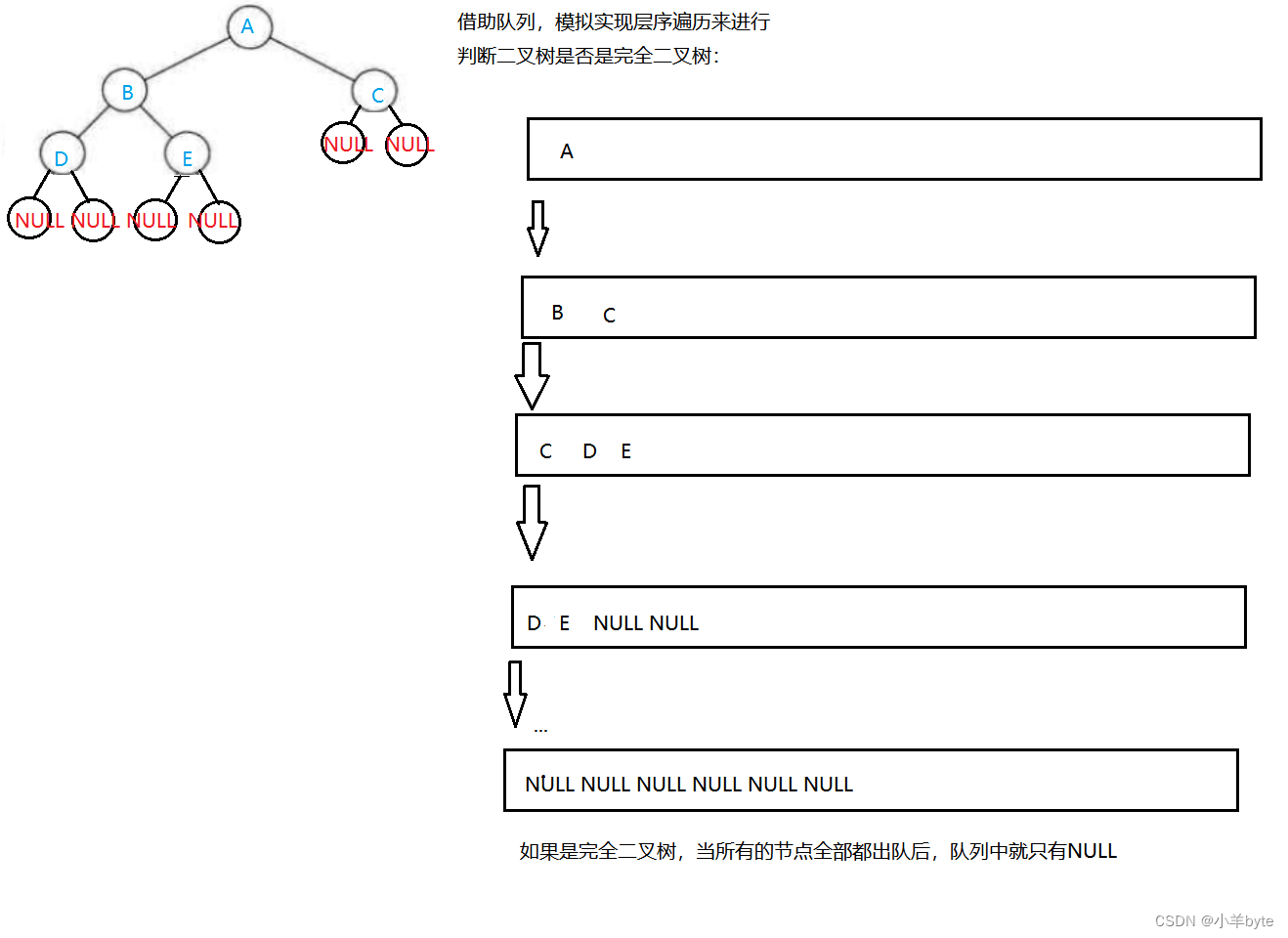
二叉树的介绍及二叉树的链式结构的实现(C语言版)
前言 二叉树是一种特殊的树,它最大的度为2,每个节点至多只有两个子树。它是一种基础的数据结构,后面很多重要的数据结构都是依靠它来进行实现的。了解并且掌握它是很重要的。 目录 1.二叉树的介绍 1.1概念 1.2现实中的二叉树 1.3特殊的二叉…...
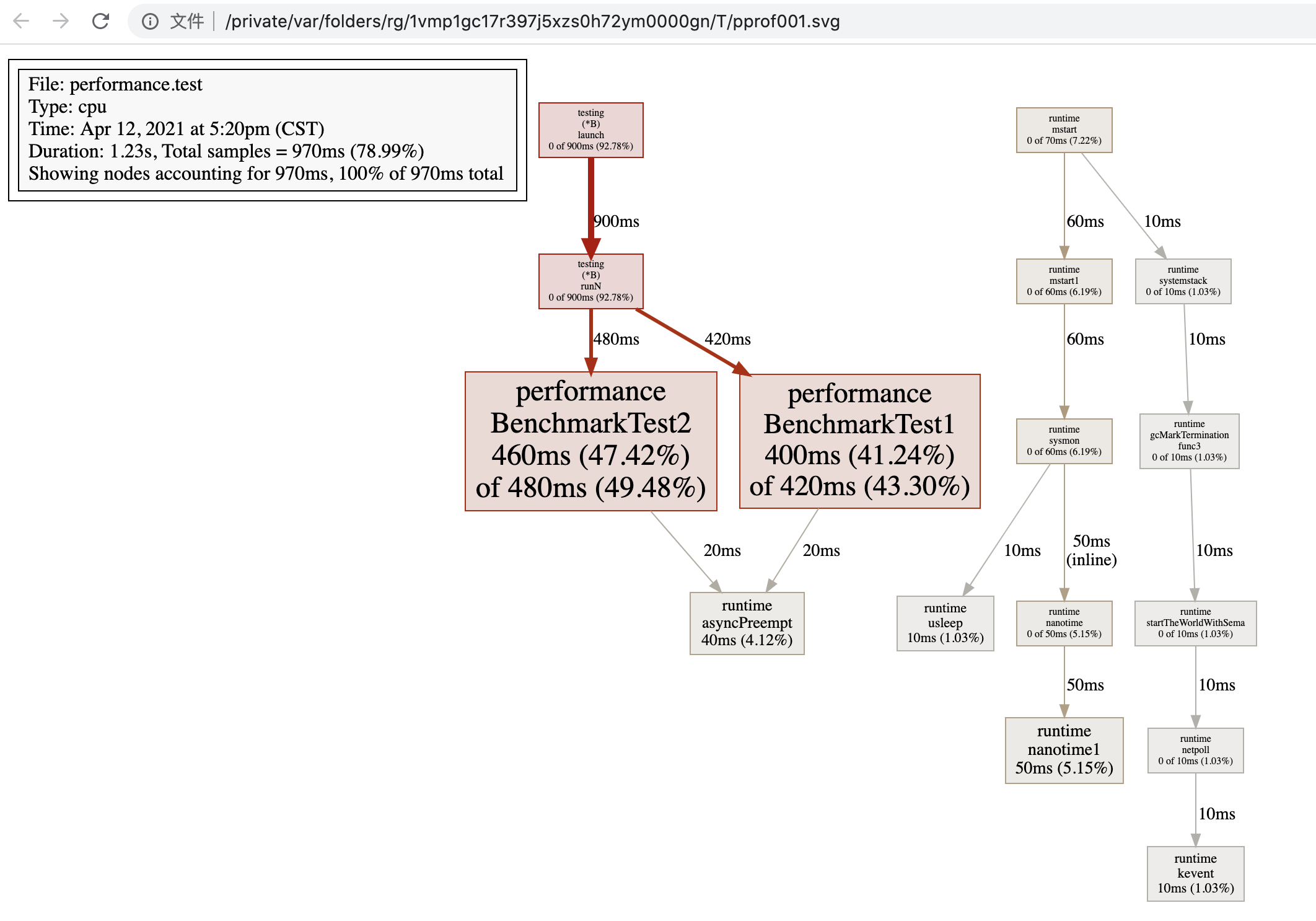
不同写法的性能差异
“ 达到相同目的,可以有多种写法,每种写法有性能、可读性方面的区别,本文旨在探讨不同写法之间的性能差异 len(str) vs str "" 本部分参考自: [问个 Go 问题,字符串 len 0 和 字符串 "" ,有啥区别?](https://segmentf…...

Bytebase 2.7.0 - 新增分支(Branching)功能
🚀 新功能 新增支持与 Git 类似的分支(Branching)功能来管理 schema 变更。支持搜索所有历史工单。支持导出审计日志。 🎄 改进 变更数据库工单详情页面全新改版。优化工单搜索体验。SQL 审核规则支持针对不同数据库进行独立配…...

day55 动规.p15 子序列
- 392.判断子序列 cpp class Solution { public: bool isSubsequence(string s, string t) { vector<vector<int>> dp(s.size() 1, vector<int>(t.size() 1, 0)); for (int i 1; i < s.size(); i) { for (int j 1; …...

TypeScript DOM类型的声明
TS DOM类型的声明 lib.dom.d.ts HTMLInputElement <input type"text" change"handleChange" /> const handleChange (evt: Event) > {console.log((evt.target as HTMLInputElement).value); } HTMLElement const div: HTMLDivElement do…...
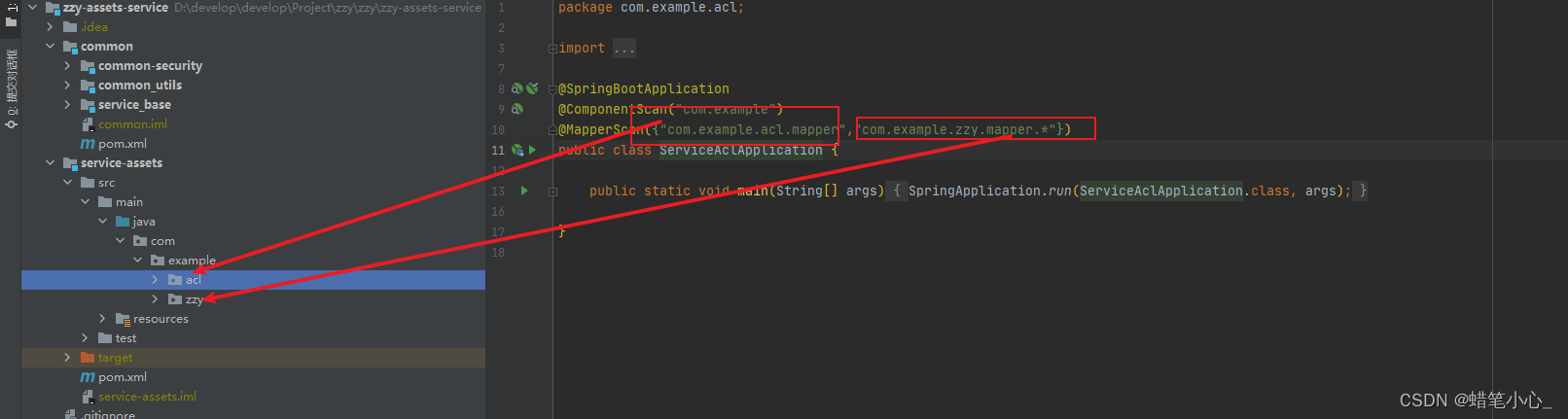
springboot找不到注册的bean
1、错误描述 A component required a bean named ‘fixedAssetsShareMapper’ that could not be found.Action:Consider defining a bean named ‘fixedAssetsShareMapper’ in your configuration.2、问题分析 1、该错误提示表明在你的应用程序中有一个组件(可能…...
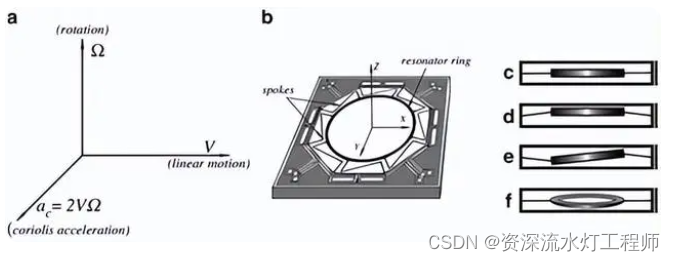
MEMS传感器的原理与构造——单片式硅陀螺仪
一、前言 机械转子式陀螺仪在很长的一段时间内都是唯一的选项,也正是因为它的结构和原理,使其不再适用于现代小型、单体、集成式传感器的设计。常规的机械转子式陀螺仪包括平衡环、支撑轴承、电机和转子等部件,这些部件需要精密加工和…...
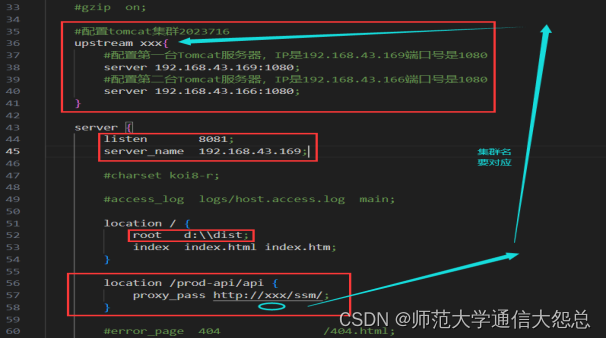
Redis集群服务器
集群简介 试想有一家餐厅,如果顾客人数较少,那么餐厅只需要一个服务员即可,如图1。但是,当顾客人数非常多时,一个服务员是绝对不够的,如图2。此时,餐厅需要雇用更多的服务员来解决大量访问&…...

动态维护直径 || 动态维护树上路径 || 涉及LCA点转序列 || 对欧拉环游序用数据结构维护:1192B
https://www.luogu.com.cn/problem/CF1192B 对于直径的求法,常用dp或两次dfs,但如果要动态维护似乎都不太方面,那么可以维护树上路径最大值。 树上路径为: d e p u d e p v − 2 d e p l c a ( u , v ) dep_udep_v-2\times de…...
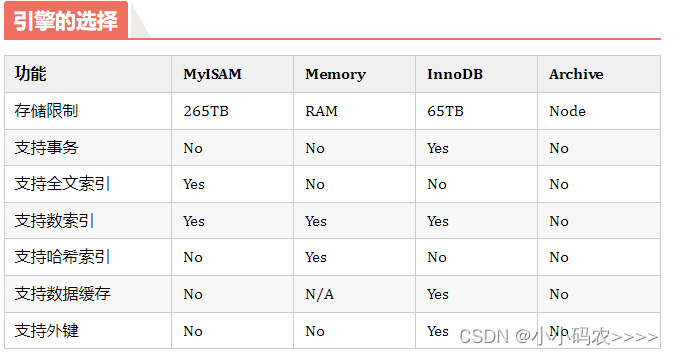
MySQL 存储引擎,你了解几个?
引言 MySQL是一种流行的关系型数据库管理系统(RDBMS),它支持多种不同的数据库引擎。数据库引擎是用于存储、管理和检索数据的核心组件,它们直接影响着数据库的性能、可靠性和功能,接下来本文介绍下一些常见的MySQL数据…...

Java 动态规划 Leetcode 740. 删除并获得点数
题目 对于该题的题目分析,已经代码分析都一并写入到了代码注释中 代码 class Solution {public int deleteAndEarn(int[] nums) {//核心思路://由于我们获得 nums[i] 的点数之后,就必须删除所有等于 nums[i] - 1 和 nums[i] 1 的元素//假设…...

算法通关村十三关-青铜:数字与数学基础问题
1.数字统计专题 统计特定场景下的符号或数字个数等 1.1符号统计 LeetCode1822 数组元素积的符号 https://leetcode.cn/problems/sign-of-the-product-of-an-array/description/ 思路分析 如果将所有的数都乘起来,再判断正负,工作量大,还…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
