当前位置： 首页 > news >正文

使用环境中的视觉地标和扩展卡尔曼滤波器定位移动机器人研究（Matlab代码实现）

news 2026/2/2 23:45:09

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码及文章

💥1 概述

本文分为6章

  • 第 1 章 基础知识： 它涵盖了运行仿真和了解差速移动机器人的基本运动学的所有基础知识。
  • 第2章 传感器： 在本章中，将学习如何实现测程法、激光雷达、物体检测等传感器以及用于避障的 VFH 等算法。
  • 第三章 路径规划： 在本课中，您将学习如何规划路径以及如何使用 RRT* 算法使机器人遵循路径（路径跟踪）。

  • 第四章 前几章小结： 在本课中，您将学习如何将所有内容组合在一起并减少前几节课中的代码。

  • 第 5 章 本地化： 在本章中，您将了解为什么需要本地化系统，然后您将实现扩展卡尔曼滤波器，了解每个步骤的理论。您可以在文件Lecture_Kalman_filter_robots.pdf中找到详细说明。

  • 第6章 ROS本地化： 在本课中，我们将向您展示本地化系统如何与 MATLAB 和 ROS 一起工作。您将学习如何使用 ROSBAG 使用正确的 EKF 参数。
  • 可以使用不同的算法，地图（地图文件夹）和更改参数来练习，以在不同的环境和情况下进行练习。

  • 移动机器人的定位是机器人导航和路径规划的关键问题之一。传统的定位方法包括里程计、惯性导航和全球定位系统（GPS），但这些方法在室内或复杂环境中存在一定的局限性。

    近年来，研究人员提出了使用环境中的视觉地标和扩展卡尔曼滤波器（EKF）来定位移动机器人的方法。这种方法利用环境中的视觉地标作为参考点，通过机器人的视觉传感器来检测和识别这些地标，并利用它们的位置信息来估计机器人的位置。

    扩展卡尔曼滤波器是一种常用的滤波器，用于估计系统的状态。在移动机器人定位中，EKF可以将视觉地标的位置信息与机器人的运动模型相结合，通过迭代更新机器人的位置估计值。这样，即使视觉地标的检测和识别存在一定的误差，EKF也能够通过状态估计来减小这些误差，提高定位的准确性。

    使用环境中的视觉地标和扩展卡尔曼滤波器定位移动机器人的研究可以应用于室内导航、自动驾驶等领域。通过合理选择视觉地标和优化EKF的参数，可以实现高精度的机器人定位。此外，还可以结合其他传感器，如激光雷达、超声波传感器等，来进一步提高定位的鲁棒性和可靠性。

    总之，使用环境中的视觉地标和扩展卡尔曼滤波器定位移动机器人的研究是一个具有挑战性和广泛应用前景的领域，对于实现智能机器人的自主导航和定位具有重要意义。

​

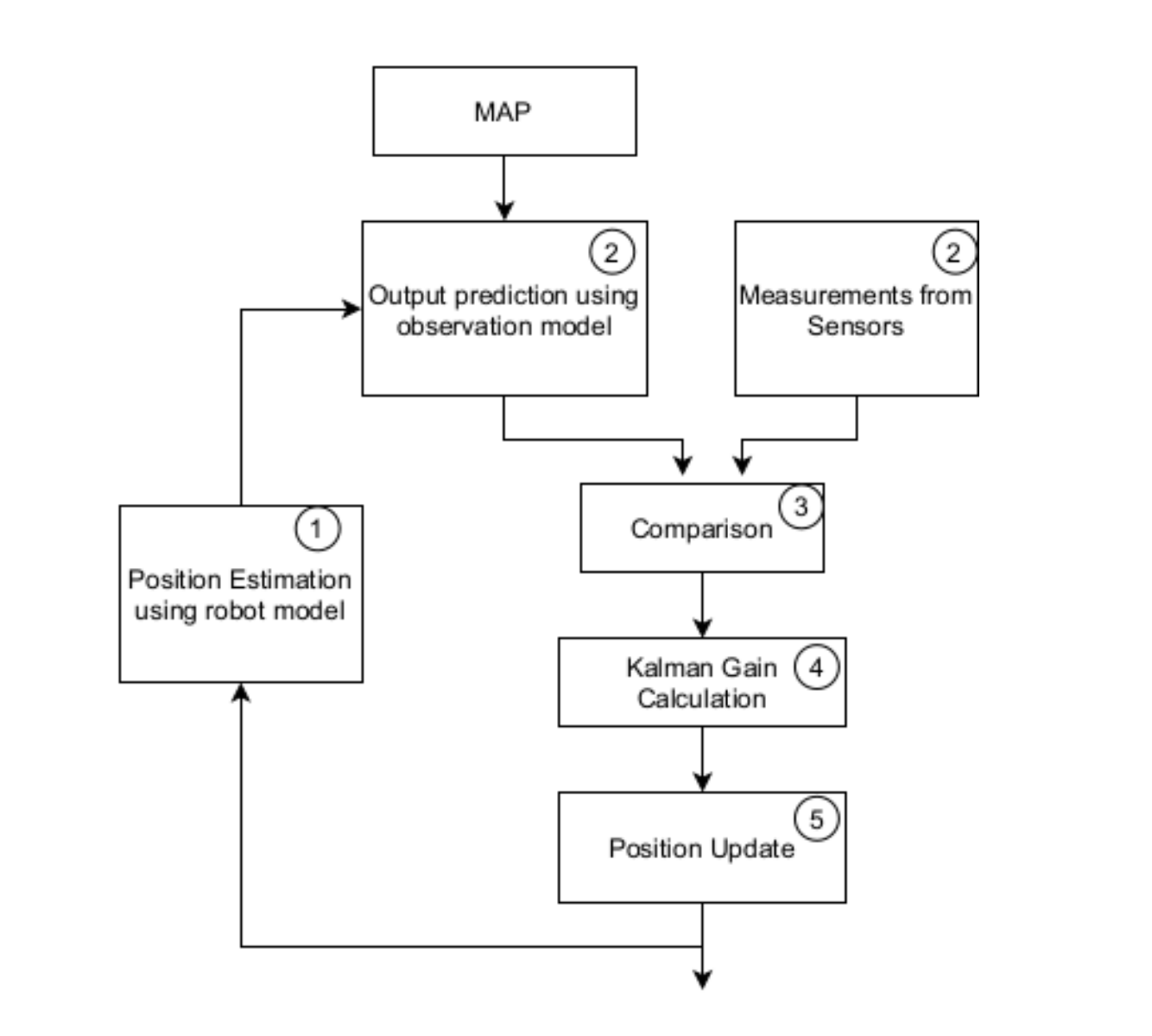
📚2 运行结果

 

 

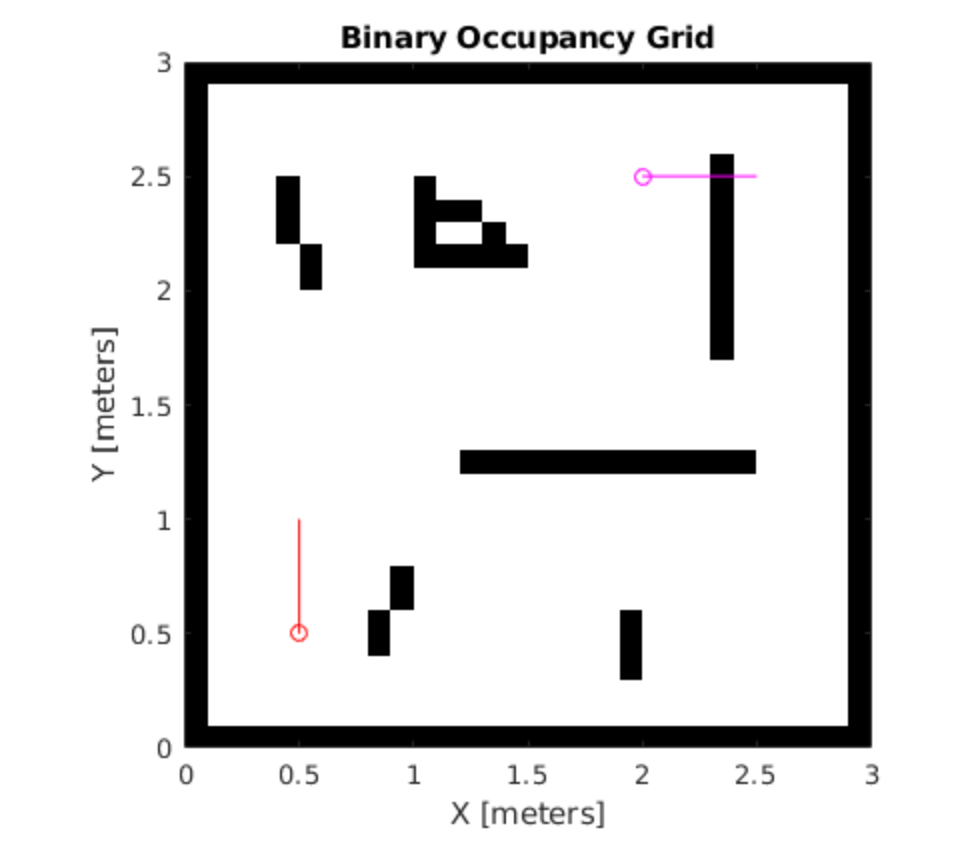
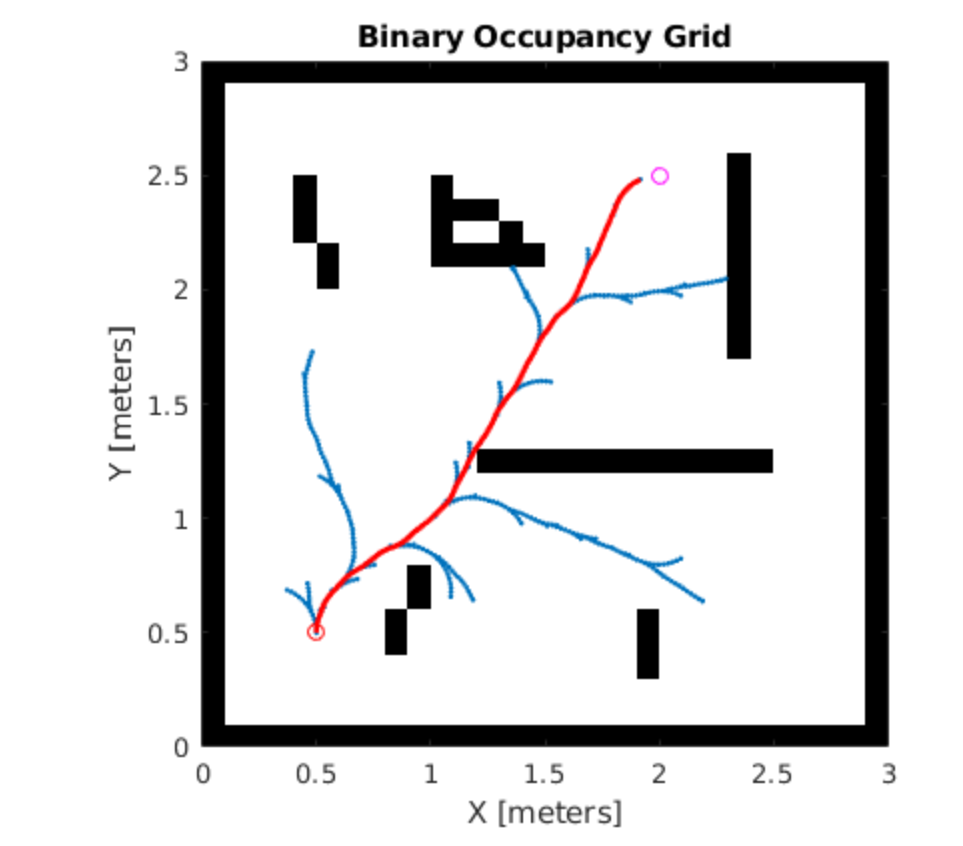
由于结果图比较多，这里仅展现3张。 

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]孟祥萍,张本法,苑全德.自适应扩展卡尔曼滤波器在移动机器人定位中的应用[J].计算机系统应用, 2015, 24(12):6.DOI:10.3969/j.issn.1003-3254.2015.12.027.

[2]时也,吴怀宇,徐文霞,等.基于扩展卡尔曼滤波器的移动机器人SLAM研究[J].电子设计工程, 2012, 20(1):3.DOI:10.3969/j.issn.1674-6236.2012.01.039.

🌈4 Matlab代码及文章

相关文章：

使用环境中的视觉地标和扩展卡尔曼滤波器定位移动机器人研究（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。 ⛳️座右铭&a…...

编程日记 2023/9/6 5:41:49

【python基础知识】5.for循环和while循环

文章目录 前言for...in...循环语句for循环：空房间for循环：一群排队办业务的人range()函数for循环：办事流程 while循环while循环：放行条件while循环：办事流程 两种循环对比 前言 上一关，我们学习了两种新的…...

编程日记 2023/9/6 5:40:48

STM32CUBEMX_创建时间片轮询架构的软件框架

STM32CUBEMX_创建时间片轮询架构的软件框架 说明： 1、这种架构避免在更新STM32CUBEMX配置后把用户代码清除掉 2、利用这种时间片的架构可以使得代码架构清晰易于维护 创建步骤： 1、使用STM32CUBEMX创建基础工程 2、新建用户代码目录 3、构建基础的代码框…...

编程日记 2023/9/6 5:39:47

vue 插槽Slots

vue插槽官网 <button class"fancy-btn"><slot></slot> <!-- 插槽出口 --> </button><slot> 元素是一个插槽出口 (slot outlet)&#xff0c;标示了父元素提供的插槽内容 (slot content) 将在哪里被渲染。 // 定义一个Child.vue…...

编程日记 2023/9/6 5:38:46

论文阅读《Nougat：Neural Optical Understanding for Academic Documents》

摘要 科学知识主要存储在书籍和科学期刊中&#xff0c;通常以PDF的形式。然而PDF格式会导致语义信息的损失&#xff0c;特别是对于数学表达式。我们提出了Nougat&#xff0c;这是一种视觉transformer模型&#xff0c;它执行OCR任务&#xff0c;用于将科学文档处理成标记语言&a…...

编程日记 2023/9/6 5:37:45

较难的换根dp:P6213 「SWTR-04」Collecting Coins

传送门 前题提要:感觉这道换根dp可以说是集中了换根dp的所有较高难度的操作和思想,以及较高的一些实现细节,可以说能够完全写出这道题才叫真正理解了换根dp,非常值得一做. 首先读完题意,不难发现这道题有很多限制.点的访问次数限制,必须访问某一个点,想要获得最大的贡献,没有…...

编程日记 2023/9/6 5:36:44

Springboot - 15.二级分布式缓存集成-Caffeine

&#x1f440;中文文档 Caffeine &#x1f440;使用Caffeine &#xff08;本地缓存&#xff09; 当与Spring Boot结合使用时&#xff0c;Caffeine提供了一个直观且功能强大的二级缓存解决方案。Spring Boot的缓存抽象使得整合Caffeine变得相当简单。以下是如何在Spring Boot…...

编程日记 2023/9/6 5:35:42

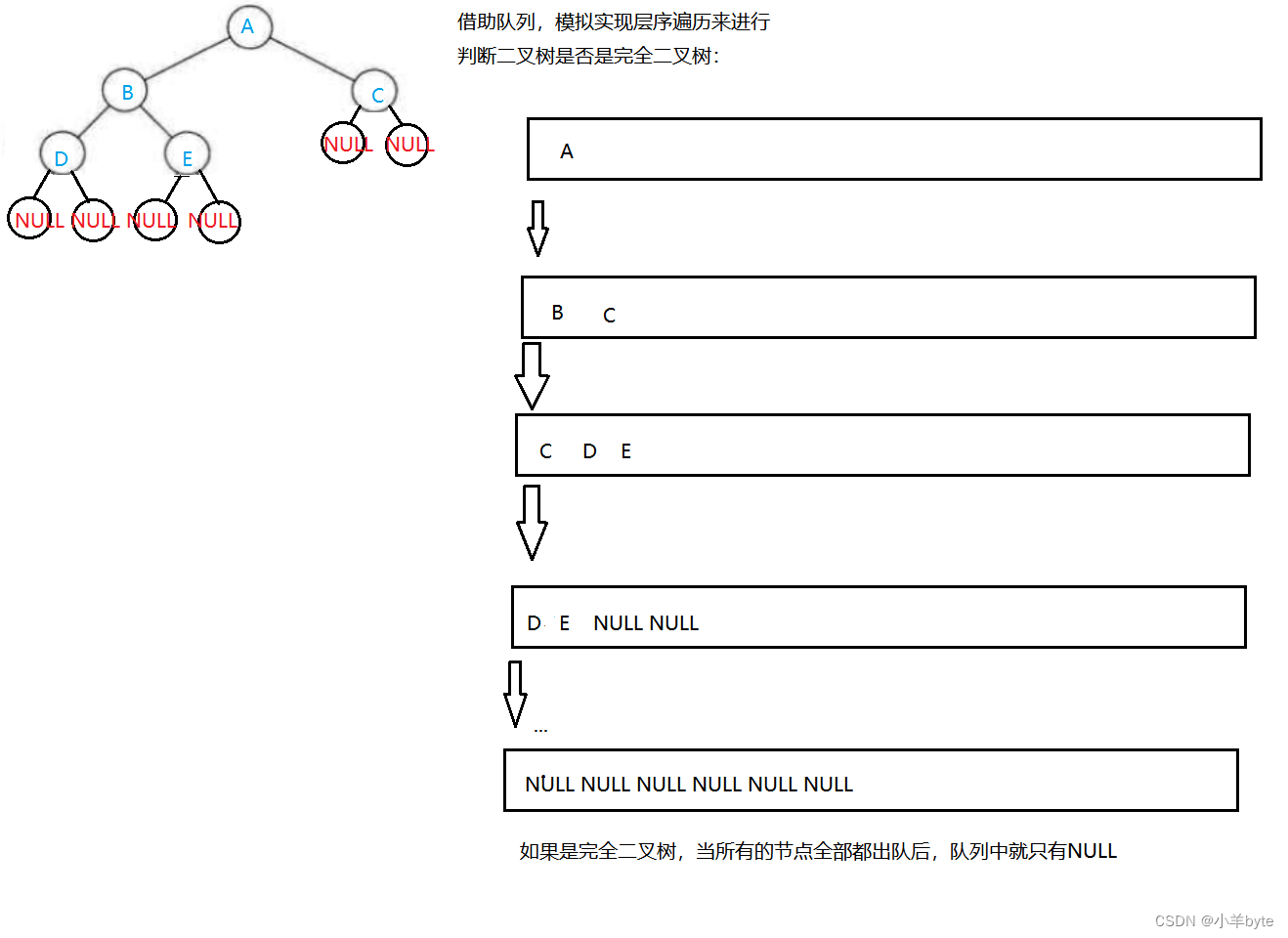
二叉树的介绍及二叉树的链式结构的实现（C语言版）

前言 二叉树是一种特殊的树&#xff0c;它最大的度为2&#xff0c;每个节点至多只有两个子树。它是一种基础的数据结构&#xff0c;后面很多重要的数据结构都是依靠它来进行实现的。了解并且掌握它是很重要的。 目录 1.二叉树的介绍 1.1概念 1.2现实中的二叉树 1.3特殊的二叉…...

编程日记 2023/9/6 5:34:39

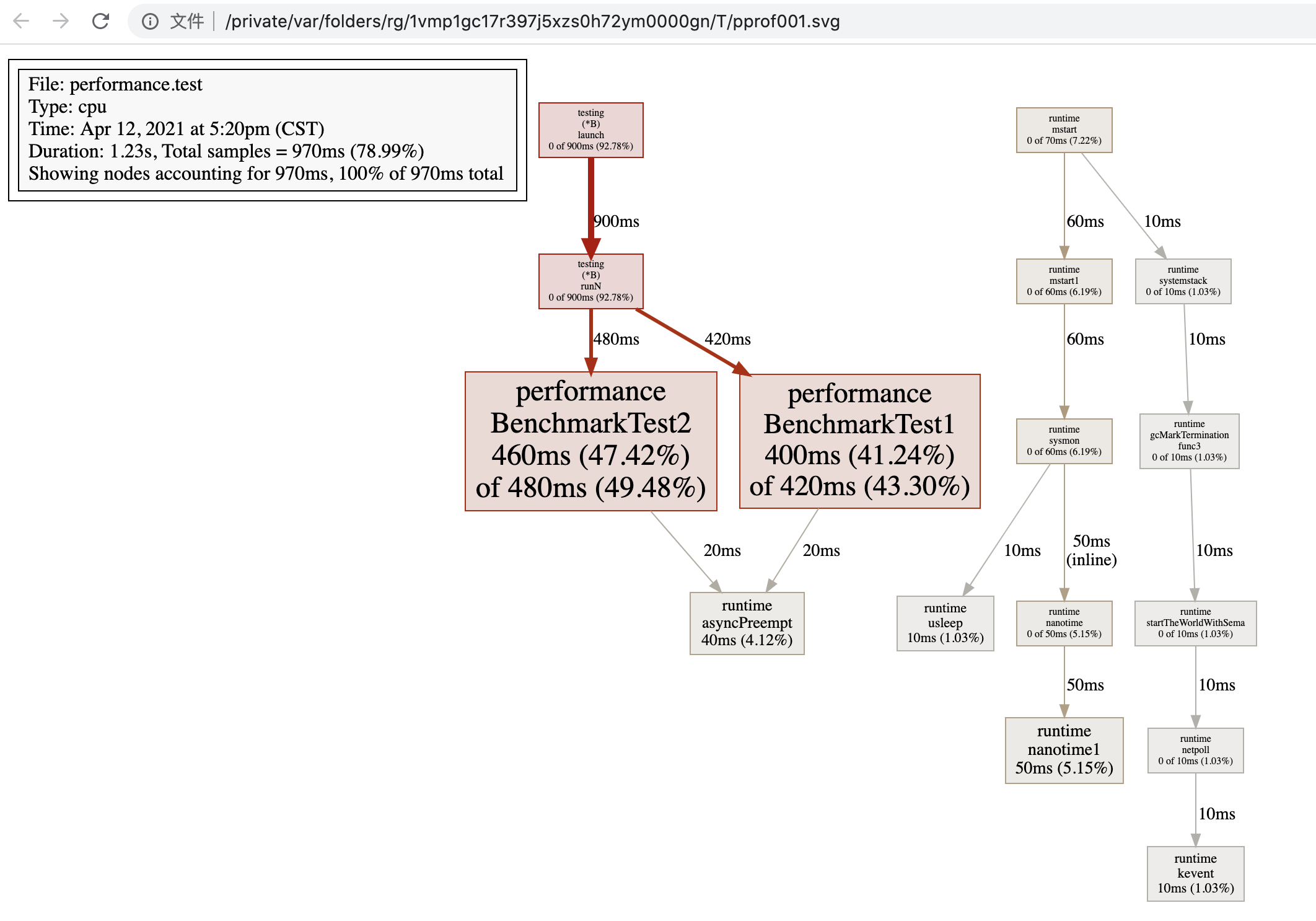
不同写法的性能差异

“ 达到相同目的,可以有多种写法,每种写法有性能、可读性方面的区别,本文旨在探讨不同写法之间的性能差异 len(str) vs str "" 本部分参考自: [问个 Go 问题&#xff0c;字符串 len 0 和 字符串 "" &#xff0c;有啥区别&#xff1f;](https://segmentf…...

编程日记 2023/9/6 5:33:37

Bytebase 2.7.0 - ​新增分支（Branching）功能

&#x1f680; 新功能 新增支持与 Git 类似的分支&#xff08;Branching&#xff09;功能来管理 schema 变更。支持搜索所有历史工单。支持导出审计日志。 &#x1f384; 改进 变更数据库工单详情页面全新改版。优化工单搜索体验。SQL 审核规则支持针对不同数据库进行独立配…...

编程日记 2023/9/6 5:32:36

day55 动规.p15 子序列

- 392.判断子序列 cpp class Solution { public: bool isSubsequence(string s, string t) { vector<vector<int>> dp(s.size() 1, vector<int>(t.size() 1, 0)); for (int i 1; i < s.size(); i) { for (int j 1; …...

编程日记 2023/9/6 5:31:35

TypeScript DOM类型的声明

TS DOM类型的声明 lib.dom.d.ts HTMLInputElement <input type"text" change"handleChange" /> const handleChange (evt: Event) > {console.log((evt.target as HTMLInputElement).value); } HTMLElement const div: HTMLDivElement do…...

编程日记 2023/9/6 5:30:34

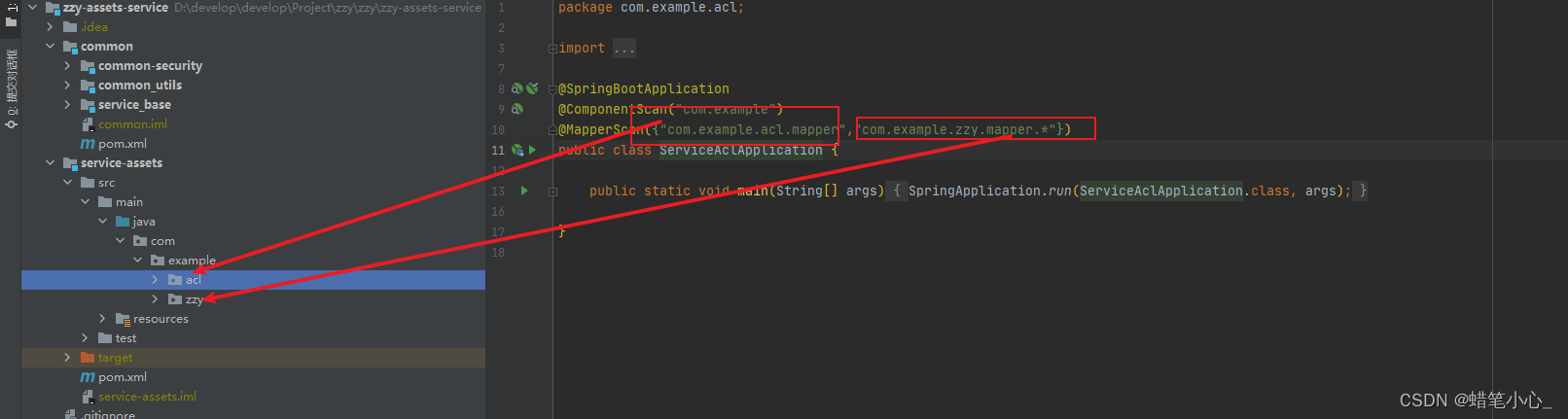
springboot找不到注册的bean

1、错误描述 A component required a bean named ‘fixedAssetsShareMapper’ that could not be found.Action:Consider defining a bean named ‘fixedAssetsShareMapper’ in your configuration.2、问题分析 1、该错误提示表明在你的应用程序中有一个组件&#xff08;可能…...

编程日记 2023/9/6 5:29:33

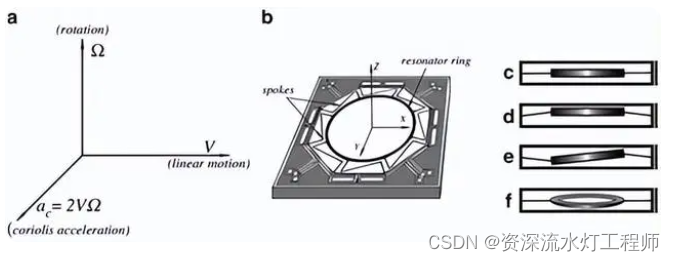
MEMS传感器的原理与构造——单片式硅陀螺仪

一、前言 机械转子式陀螺仪在很长的一段时间内都是唯一的选项&#xff0c;也正是因为它的结构和原理&#xff0c;使其不再适用于现代小型、单体、集成式传感器的设计。常规的机械转子式陀螺仪包括平衡环、支撑轴承、电机和转子等部件&#xff0c;这些部件需要精密加工和…...

编程日记 2023/9/6 5:28:31

Redis集群服务器

集群简介 试想有一家餐厅&#xff0c;如果顾客人数较少&#xff0c;那么餐厅只需要一个服务员即可&#xff0c;如图1。但是&#xff0c;当顾客人数非常多时&#xff0c;一个服务员是绝对不够的&#xff0c;如图2。此时&#xff0c;餐厅需要雇用更多的服务员来解决大量访问&…...

编程日记 2023/9/6 5:27:29

动态维护直径 || 动态维护树上路径 || 涉及LCA点转序列 || 对欧拉环游序用数据结构维护：1192B

https://www.luogu.com.cn/problem/CF1192B 对于直径的求法&#xff0c;常用dp或两次dfs&#xff0c;但如果要动态维护似乎都不太方面&#xff0c;那么可以维护树上路径最大值。 树上路径为&#xff1a; d e p u d e p v − 2 d e p l c a ( u , v ) dep_udep_v-2\times de…...

编程日记 2023/9/6 5:26:28

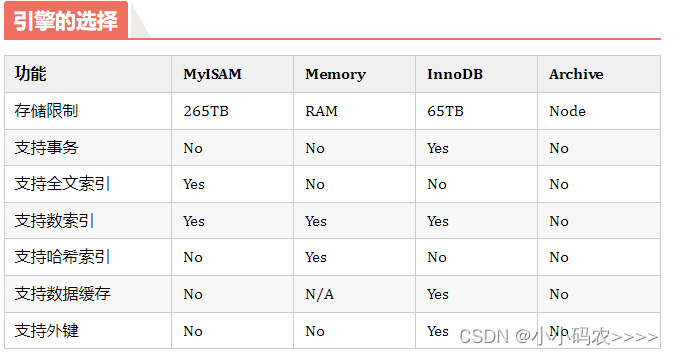
MySQL 存储引擎，你了解几个？

引言 MySQL是一种流行的关系型数据库管理系统&#xff08;RDBMS&#xff09;&#xff0c;它支持多种不同的数据库引擎。数据库引擎是用于存储、管理和检索数据的核心组件&#xff0c;它们直接影响着数据库的性能、可靠性和功能&#xff0c;接下来本文介绍下一些常见的MySQL数据…...

编程日记 2023/9/6 5:25:27

Java 动态规划 Leetcode 740. 删除并获得点数

题目 对于该题的题目分析&#xff0c;已经代码分析都一并写入到了代码注释中 代码 class Solution {public int deleteAndEarn(int[] nums) {//核心思路&#xff1a;//由于我们获得 nums[i] 的点数之后&#xff0c;就必须删除所有等于 nums[i] - 1 和 nums[i] 1 的元素//假设…...

编程日记 2023/9/6 5:24:26

算法通关村十三关-青铜：数字与数学基础问题

1.数字统计专题 统计特定场景下的符号或数字个数等 1.1符号统计 LeetCode1822 数组元素积的符号 https://leetcode.cn/problems/sign-of-the-product-of-an-array/description/ 思路分析 如果将所有的数都乘起来&#xff0c;再判断正负&#xff0c;工作量大&#xff0c;还…...

编程日记 2023/9/6 5:23:24

猜拳游戏小程序源码 大转盘积分游戏小程序源码 积分游戏小程序源码

简介&#xff1a; 猜拳游戏大转盘积分游戏小程序前端模板源码&#xff0c;一共五个静态页面&#xff0c;首页、任务列表、大转盘和猜拳等五个页面 图片&#xff1a;...

编程日记 2023/9/6 5:22:23

MPNet：旋转机械轻量化故障诊断模型详解python代码复现

目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块（MBFM） 2.2 残差注意力金字塔模块（RAPM） 2.2.1 空间金字塔注意力（SPA） 2.2.2 金字塔残差块（PRBlock） 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

编程新知 2026/1/31 16:21:10

vscode里如何用git

打开vs终端执行如下&#xff1a; 1 初始化 Git 仓库&#xff08;如果尚未初始化&#xff09; git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

Android Wi-Fi 连接失败日志分析

1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分&#xff1a; 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析&#xff1a; CTR…...

编程新知 2025/9/14 19:44:52

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2026/1/21 14:29:57

DeepSeek 赋能智慧能源：微电网优化调度的智能革新路径

目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

编程新知 2025/11/20 2:48:44

【Java学习笔记】Arrays类

Arrays 类 1. 导入包&#xff1a;import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序&#xff08;自然排序和定制排序&#xff09;Arrays.binarySearch()通过二分搜索法进行查找&#xff08;前提&#xff1a;数组是…...

编程新知 2025/12/3 9:38:15

深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法

深入浅出&#xff1a;JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中&#xff0c;随机数的生成看似简单&#xff0c;却隐藏着许多玄机。无论是生成密码、加密密钥&#xff0c;还是创建安全令牌&#xff0c;随机数的质量直接关系到系统的安全性。Jav…...

编程新知 2025/10/8 4:56:09

什么是库存周转？如何用进销存系统提高库存周转率？

你可能听说过这样一句话&#xff1a; “利润不是赚出来的&#xff0c;是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业&#xff0c;很多企业看着销售不错&#xff0c;账上却没钱、利润也不见了&#xff0c;一翻库存才发现&#xff1a; 一堆卖不动的旧货…...

编程新知 2026/1/26 13:21:10

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式

点一下关注吧&#xff01;&#xff01;&#xff01;非常感谢&#xff01;&#xff01;持续更新&#xff01;&#xff01;&#xff01; &#x1f680; AI篇持续更新中&#xff01;&#xff08;长期更新&#xff09; 目前2025年06月05日更新到&#xff1a; AI炼丹日志-28 - Aud…...

编程新知 2026/1/31 6:06:30

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序

一、开发环境准备 ​​工具安装​​&#xff1a; 下载安装DevEco Studio 4.0&#xff08;支持HarmonyOS 5&#xff09;配置HarmonyOS SDK 5.0确保Node.js版本≥14 ​​项目初始化​​&#xff1a; ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

编程新知 2026/2/1 4:17:33