二叉树的介绍及二叉树的链式结构的实现(C语言版)
前言
二叉树是一种特殊的树,它最大的度为2,每个节点至多只有两个子树。它是一种基础的数据结构,后面很多重要的数据结构都是依靠它来进行实现的。了解并且掌握它是很重要的。
目录
1.二叉树的介绍
1.1概念
1.2现实中的二叉树
1.3特殊的二叉树
1.4二叉树的性
1.5二叉树的存储结构
2.二叉树链式结构的实现
2.1创建一颗伪二叉树
2.2二叉树的遍历
2.2.1前序,中序和后序遍历
2.2.2层序遍历
2.3二叉树的节点个数及高度等
2.4二叉树的创建及销毁
2.5全部代码
1.二叉树的介绍
1.1概念
一颗二叉树是节点的一个有限集合,该集合:
1.或者为空
2.由根节点外加两颗别称为左子树和右子树的二叉树组成
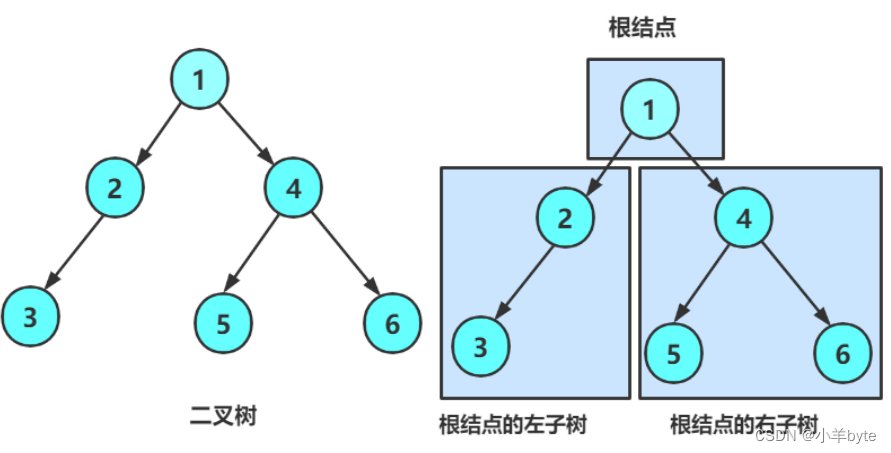
1.2现实中的二叉树


1.3特殊的二叉树
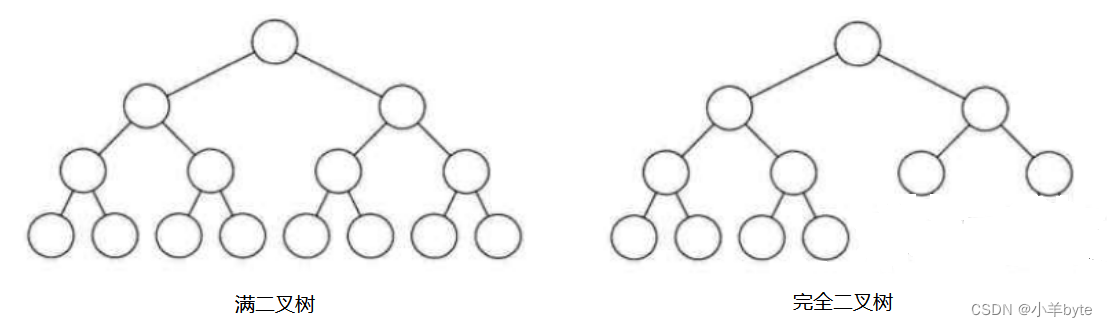
满二叉树:一个二叉树,如果每一层的节点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且节点的总数是二的K次方-1,则它就是满二叉树。
完全二叉树 : 完全二叉树是一种效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有N个节点的二叉树,当且仅当每个节点都与深度为K的满二叉树中编号从1到N的节点一一对应时,称为完全二叉树。
1.4二叉树的性
1.若规定根节点的层数为1,则一颗非空二叉树的第i层最多有2的i-1次方个节点。
2.若规定根节点的层数为1,则深度为h的二叉树最大的节点数为2的h次方减1。
3.对于任意一颗二叉树,如果度为零其叶子结点的个数为n0,度为2的分支节点个数为n2,则有n0 = n2 + 1;
4.若规定根节点的层数为1,其n个节点的满二叉树的深度,h = log2(n+1).(log2(n + 1)是以2为底,n+1为对数);
5.对于具有n个节点的完全二叉树,如果按照从上至下,从左至右的数组顺序对所有的节点从0开始编号,则对于序号为i的节点有:
1.若i大于0,i位置双亲节点的序号:(i - 1)/2; i = 0,i为根节点编号,无双亲节点
2.若2i+1<n,左孩子的序号:2i+1;2i+1>=n,则无左孩子。
3.若2i+2<n,右孩子序号:2i+2,2i+2>=n,则无右孩子。
1.5二叉树的存储结构
二叉树一般有两种结构的存储方式,一种是顺序结构,一种是链式结构。
1.顺序存储
顺序存储使用的数组,一般数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费,而现实中只有堆 才使用数组来存储。二叉树的顺序存储在物理上是数组,在逻辑上是一颗二叉树。
2.链式存储
二叉树的链式存储结构是指,用链表来表示一颗二叉树,即用链表来指示元素之间的逻辑关系。通常的方法是每个节点由左,右指针域和数据域组成。左,右指针分别用来给出该节点左孩子和右孩子所在节点的地址。链式存储结构又分为二叉链和三叉链。现在我们使用的是二叉链。


2.二叉树链式结构的实现
2.1创建一颗伪二叉树
这里需要快速创建一颗二叉树,为了降低理解的难度,先创建一颗伪二叉树来进行学习,便于理解。
//BTree.h
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef char BTDataType;
typedef struct BTreeNode
{BTDataType _data;struct BTreeNode* _left;struct BTreeNode* _right;
}BTreeNode;
BTreeNode* BuyBTreeNode(BTreeNode* node, BTDataType c);//申请一棵树的节点BTreeNode* CreatBinaryTree(BTreeNode* root);//创建一棵树//BTree.c
BTreeNode* BuyBTreeNode(BTreeNode* node,BTDataType c)
{BTreeNode*cur = (BTreeNode*)malloc(sizeof(BTreeNode));cur->_data = c;cur->_left = cur->_right = NULL;
}
BTreeNode* CreatBinaryTree(BTreeNode* root)//创建一棵树
{root = BuyBTreeNode(root, 'A');BTreeNode* B = BuyBTreeNode(root, 'B');BTreeNode* C = BuyBTreeNode(root, 'C');BTreeNode* D = BuyBTreeNode(root, 'D');BTreeNode* E = BuyBTreeNode(root, 'E');BTreeNode* F = BuyBTreeNode(root, 'F');root->_left = B;root->_right = C;B->_left = D;C->_left = E;C->_right = F;return root;
}2.2二叉树的遍历
2.2.1前序,中序和后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树的遍历就是按照某种特定的规则,依次对二叉树的节点进行相应的操作,并且每个节点只操作一次。访问节点的操作依赖于具体的问题,遍历是二叉树上最重要的运算之一,也是二叉树进行其他运算的基础。
按照规则二叉树的遍历有:前序,中序和后序的递归结构遍历:
1.前序遍历(Preorder Traversal ),亦称为先序遍历,访问根节点的操作发生在访问左右子树之前。
2.中序遍历(Inorder Traversal)--访问根节点的操作发生在访问左右子树之间。
3.后序遍历(Post Traversal)--访问根节点的操作发生在左右子树之后。
由于被访问的节点必是某树的根,所以N(Node) ,L(Left subtree)和R(Right subtree)又可以解释为,根节点,根的左子树和根的右子树。NLR,LNR,LRN分别称为先根遍历,中根遍历和后根遍历。
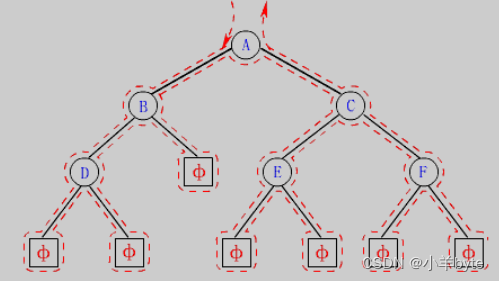
前序遍历的代码:
// 二叉树前序遍历
void PreOrder(BTreeNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ",root->_data);PreOrder(root->_left);//左子树PreOrder(root->_right);//右子树
}前序遍历的递归图解:


中序遍历和后序遍历的代码:
// 二叉树中序遍历
void InOrder(BTreeNode* root)
{if (root == NULL){printf("NULL ");return;}PreOrder(root->_left);//左子树printf("%c ", root->_data);//根PreOrder(root->_right);//右子树
}
// 二叉树后序遍历
void PostOrder(BTreeNode* root)
{if (root == NULL){printf("NULL ");return;}PreOrder(root->_left);//左子树PreOrder(root->_right);//右子树printf("%c ", root->_data);//根}中序和后序遍历的展开图解和前序遍历的类似,有兴趣的友友可以自己画画看。
2.2.2层序遍历
二叉树的层序遍历是通过借助队列来实现的,将一颗树的根入队,出队时,如果根的左,右节点不为空就将根的左右节点依次入队,当队列为空时结束循环,这样就完成了二叉树的层序遍历。
void LevelOrder(BTreeNode* root)//层序遍历
{//创建队列Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q))//队列不为空,出队头的元素,同时取节点判断左右子树是否为空{BTreeNode* cur = QueueFront(&q);QueuePop(&q);printf("%c ", cur->_data);if (cur->_left)//左子树存在{QueuePush(&q, cur->_left);//将当前节点的左子树入队}if (cur->_right)//右子树存在{QueuePush(&q, cur->_right);//将当前节点的右子树入队}}
}2.3二叉树的节点个数及高度等
递归求二叉树的高度是在当前节点求出左,右子树的高度,再将左,右子树中高度大的那个加一就是当前树的高度。
int BinarTreelen(BTreeNode* root)//求树的高度
{if (root == NULL)return 0;int leftsize = BinarTreelen(root->_left);int rightsize = BinarTreelen(root->_right);return leftsize > rightsize ? leftsize + 1 : rightsize + 1;//高度等于下一层左右节点高的那个加1
}二叉树叶子结点的个数,通过递归求解,首先叶子节点肯定满足左右子树都为空,所以如果左右子树都为空的话,就直接返回1,说明当前节点就是叶子节点,否则继续递归去找叶子节点。
int BinaryTreeLeafSize(BTreeNode* root)
{if (root == NULL)//节点为空直接返回return 0;if (root->_left == NULL && root->_right == NULL)//左右节点都为空return 1;//说明当前节点为叶子节点return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);//递归去求左右子树
}求二叉树的节点个数,如果当前节点不为空,就+1,然后递归求左,右子树中的节点数。如果当前节点为NULL则返回0.
// 二叉树节点个数
int BinaryTreeSize(BTreeNode* root)
{if (root == NULL)//当前节点为NULLreturn 0;return 1 + BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right);//前序遍历的方式求树的节点个数
}二叉树查找值为x的节点,通过前序遍历二叉树,如果二叉树当前节点的值等于x就返回当前节点。
BTreeNode* BinaryTreeFind(BTreeNode* root, BTDataType x)
{if (root == NULL)//如果节点为NULLreturn NULL;//返回NULLif (root->_data == x)return root;//找到值为x的节点,返回BTreeNode*cur = BinaryTreeFind(root->_left, x);if (cur)//找到了就返回节点的地址return cur;cur = BinaryTreeFind(root->_right, x);if (cur)//找到了就返回节点的地址return cur;return NULL;//如果这棵树没有找到就返回NULL
}求二叉树的第K层的节点个数,采用分治的思想:一颗树第K层的节点等于左子树K-1层的节点+右子树K-1层的节点。 结束条件是,如果当K等于1时,返回1,当当前节点为NULL时返回0。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTreeNode* root, int _k)
{if (root == NULL)return 0;if (_k == 1 && root)//如果K等于1直接返回return 1;return BinaryTreeLevelKSize(root->_left, _k - 1) + BinaryTreeLevelKSize(root->_right, _k - 1);//递归到左,右子树K-1层中去找节点数
}判断一颗二叉树是不是完全二叉树,借助 队列,采用层序遍历的方式,但是这里不判断当前树的左右子树是否为空,取队头的数据时,直接将该节点的左,右子树入队。当取到的队头的数据为空时,结束循环。如果是完全二叉树,那么剩余在队列中的所有的NULL应该是连续的。再将队列中所有的元素都出队,如果全部为空就满足完全二叉树,如果不是就不满足完全二叉树。
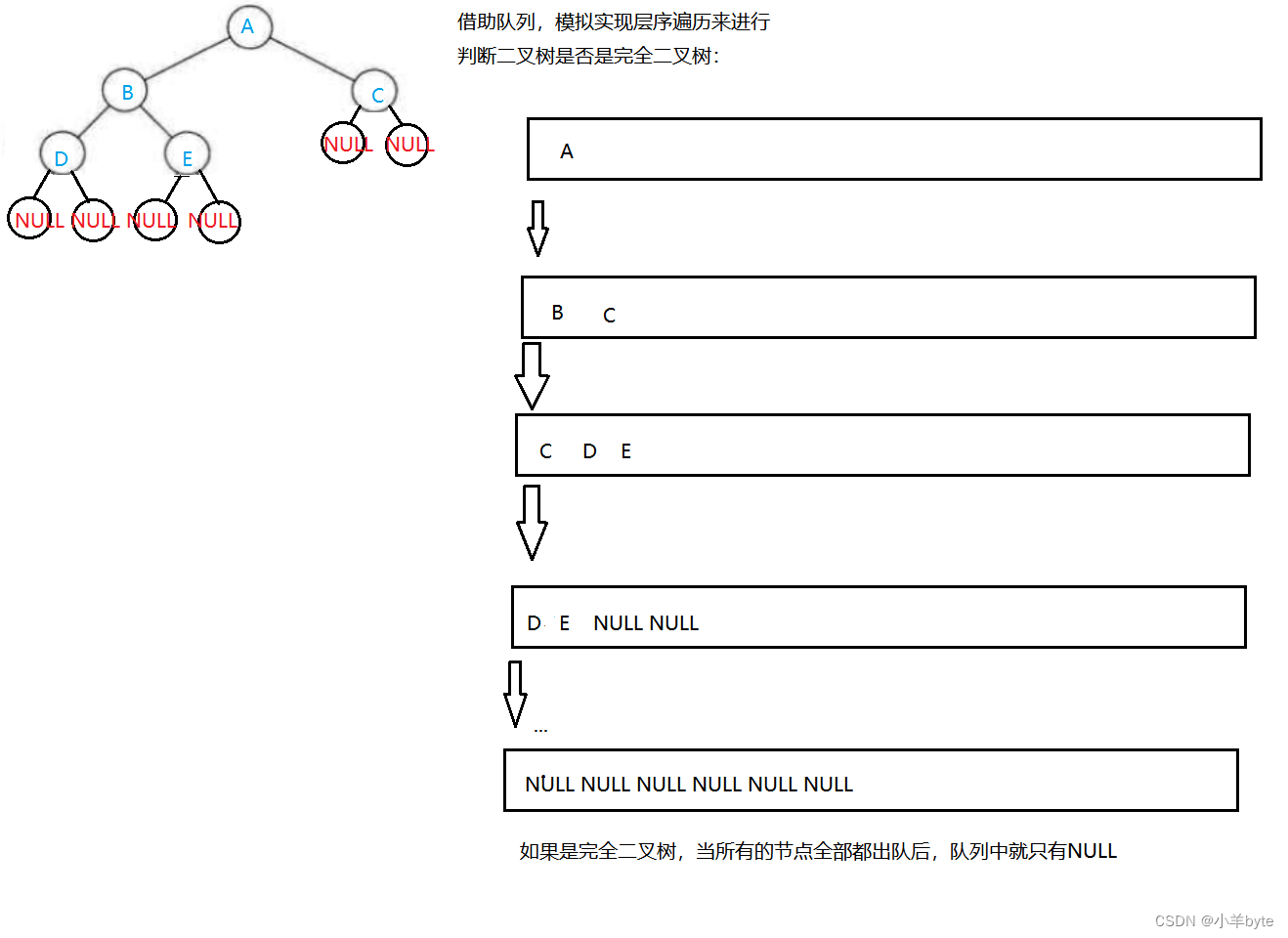
bool BinaryTreeComplete(BTreeNode* root)//判断一棵树是不是完全二叉树
{if (root == NULL)return true;//创建队列Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q))//队列不为空,出队头的元素,同时判断取出来的节点是否为空{BTreeNode* cur = QueueFront(&q);QueuePop(&q);if (cur == NULL)break;//当前节点为空直接结束循环QueuePush(&q, cur->_left);QueuePush(&q, cur->_right);}while (!QueueEmpty(&q)){//判断队列中剩下的元素是否有不为空的BTreeNode* cur = QueueFront(&q);QueuePop(&q);if (cur)return false;}//如果走到这里还没有返回说明是完全二叉树return true;
}2.4二叉树的创建及销毁
通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树。
思路:通过递归去构建二叉树,因为给出的是前序遍历的数组,而数组中的#表示NULL,因此需要参数来记录数组的位置,也需要将字符数组传递给构建函数,如果遇到#就返回NULL,如果不是就申请空间初始化data域,并且将申请的空间进行返回,然后去递归构建左右子树。
#include <stdio.h>
#include<stdlib.h>typedef struct BTreeNode
{char _data;struct BTNode* _left;struct BTNode* _right;}BTreeNode;void InOrder(BTreeNode* root){if (root == NULL)return;//左子树InOrder(root->_left);//根printf("%c ", root->_data);//右子树InOrder(root->_right);
}BTreeNode* BinaryTreeCreate(char* a, int* pi)
{if (a[*pi] == '#'){++(*pi);return NULL;}BTreeNode* node = (BTreeNode*)malloc(sizeof(BTreeNode));//申请节点node->_data = a[*pi];(*pi)++;//递归构建左右子树node->_left = BinaryTreeCreate(a, pi);node->_right = BinaryTreeCreate(a, pi);return node;
}
int main()
{char s[50] = { 0 };scanf("%s", s);int i = 0;//使用前序遍历构建树BTreeNode* root = BinaryTreeCreate(s, &i);//使用中序遍历打印树的节点的值InOrder(root);return 0;
}二叉树的销毁,如果采用前序遍历的方式进行销毁,就需要保存当前节点,所以建议采用后序遍历的方式进行销毁。
// 二叉树销毁
void BinaryTreeDestory(BTreeNode* root)//这里为了保持接口的一致性采用一级指针
{if (root == NULL)return;BinaryTreeDestory(root->_left);BinaryTreeDestory(root->_right);free(root);
}
2.5全部代码
//BTree.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<stdbool.h>
typedef char BTDataType;
typedef struct BTreeNode
{BTDataType _data;struct BTreeNode* _left;struct BTreeNode* _right;
}BTreeNode;
BTreeNode* BuyBTreeNode(BTreeNode* node, BTDataType c);//申请一棵树的节点BTreeNode* CreatBinaryTree(BTreeNode* root);//创建一棵树// 二叉树前序遍历
void PreOrder(BTreeNode* root);
// 二叉树中序遍历
void InOrder(BTreeNode* root);
// 二叉树后序遍历
void PostOrder(BTreeNode* root);// 二叉树节点个数
int BinaryTreeSize(BTreeNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTreeNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTreeNode* root, int _k);int BinarTreelen(BTreeNode* root);//求树的高度
// 二叉树查找值为x的节点
BTreeNode* BinaryTreeFind(BTreeNode* root, BTDataType x);void LevelOrder(BTreeNode* root);//层序遍历// 二叉树销毁
void BinaryTreeDestory(BTreeNode* root);
bool BinaryTreeComplete(BTreeNode* root);//判断一棵树是不是完全二叉树
//BTree.c
#include"BTree.h"
#include"Queue.h"
BTreeNode* BuyBTreeNode(BTreeNode* node,BTDataType c)
{BTreeNode*cur = (BTreeNode*)malloc(sizeof(BTreeNode));cur->_data = c;cur->_left = cur->_right = NULL;return cur;
}
BTreeNode* CreatBinaryTree(BTreeNode* root)//创建一棵树
{root = BuyBTreeNode(root, 'A');BTreeNode* B = BuyBTreeNode(root, 'B');BTreeNode* C = BuyBTreeNode(root, 'C');BTreeNode* D = BuyBTreeNode(root, 'D');BTreeNode* E = BuyBTreeNode(root, 'E');BTreeNode* F = BuyBTreeNode(root, 'F');root->_left = B;root->_right = C;B->_left = D;C->_left = E;C->_right = F;return root;
}
// 二叉树前序遍历
void PreOrder(BTreeNode* root){if (root == NULL){ return;}printf("%c ",root->_data);PreOrder(root->_left);//左子树PreOrder(root->_right);//右子树
}
// 二叉树中序遍历
void InOrder(BTreeNode* root)
{if (root == NULL){printf("NULL ");return;}PreOrder(root->_left);//左子树printf("%c ", root->_data);//根PreOrder(root->_right);//右子树
}
// 二叉树后序遍历
void PostOrder(BTreeNode* root)
{if (root == NULL){printf("NULL ");return;}PreOrder(root->_left);//左子树PreOrder(root->_right);//右子树printf("%c ", root->_data);//根}// 二叉树节点个数
int BinaryTreeSize(BTreeNode* root)
{if (root == NULL)//当前节点为NULLreturn 0;return 1 + BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right);//前序遍历的方式求树的节点个数
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTreeNode* root)
{if (root == NULL)//节点为空直接返回return 0;if (root->_left == NULL && root->_right == NULL)//左右节点都为空return 1;//说明当前节点为叶子节点return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);//递归去求左右子树
}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTreeNode* root, int _k)
{if (root == NULL)return 0;if (_k == 1 && root)//如果K等于1直接返回return 1;return BinaryTreeLevelKSize(root->_left, _k - 1) + BinaryTreeLevelKSize(root->_right, _k - 1);//递归到左,右子树K-1层中去找节点数
}
int BinarTreelen(BTreeNode* root)//求树的高度
{if (root == NULL)return 0;int leftsize = BinarTreelen(root->_left);int rightsize = BinarTreelen(root->_right);return leftsize > rightsize ? leftsize + 1 : rightsize + 1;//高度等于下一层左右节点高的那个加1
}
// 二叉树查找值为x的节点BTreeNode* BinaryTreeFind(BTreeNode* root, BTDataType x)
{if (root == NULL)//如果节点为NULLreturn NULL;//返回NULLif (root->_data == x)return root;//找到值为x的节点,返回BTreeNode*cur = BinaryTreeFind(root->_left, x);if (cur)//找到了就返回节点的地址return cur;cur = BinaryTreeFind(root->_right, x);if (cur)//找到了就返回节点的地址return cur;return NULL;//如果这棵树没有找到就返回NULL
}void LevelOrder(BTreeNode* root)//层序遍历
{//创建队列Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q))//队列不为空,出队头的元素,同时取节点判断左右子树是否为空{BTreeNode* cur = QueueFront(&q);QueuePop(&q);printf("%c ", cur->_data);if (cur->_left)//左子树存在{QueuePush(&q, cur->_left);}if (cur->_right)//右子树存在{QueuePush(&q, cur->_right);}}
}// 二叉树销毁
void BinaryTreeDestory(BTreeNode* root)//这里为了保持接口的一致性采用一级指针
{if (root == NULL)return;BinaryTreeDestory(root->_left);BinaryTreeDestory(root->_right);free(root);
}
bool BinaryTreeComplete(BTreeNode* root)//判断一棵树是不是完全二叉树
{if (root == NULL)return true;//创建队列Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q))//队列不为空,出队头的元素,同时判断取出来的节点是否为空{BTreeNode* cur = QueueFront(&q);QueuePop(&q);if (cur == NULL)break;//当前节点为空直接结束循环QueuePush(&q, cur->_left);QueuePush(&q, cur->_right);}while (!QueueEmpty(&q)){//判断队列中剩下的元素是否有不为空的BTreeNode* cur = QueueFront(&q);QueuePop(&q);if (cur)return false;}//如果走到这里还没有返回说明是完全二叉树return true;
}#include <stdio.h>
#include<stdlib.h>typedef struct BTreeNode
{char _data;struct BTNode* _left;struct BTNode* _right;}BTreeNode;void InOrder(BTreeNode* root){if (root == NULL)return;//左子树InOrder(root->_left);//根printf("%c ", root->_data);//右子树InOrder(root->_right);
}BTreeNode* BinaryTreeCreate(char* a, int* pi)
{if (a[*pi] == '#'){++(*pi);return NULL;}BTreeNode* node = (BTreeNode*)malloc(sizeof(BTreeNode));//申请节点node->_data = a[*pi];(*pi)++;//递归构建左右子树node->_left = BinaryTreeCreate(a, pi);node->_right = BinaryTreeCreate(a, pi);return node;
}
//Queue.h
#pragma once
#include<stdlib.h>
#include<assert.h>
#include<stdio.h>
#include<stdbool.h>
typedef struct BTreeNode BTreeNode;
typedef BTreeNode* QDataType;//树节点的声明typedef struct QueueNode
{struct QueueNode* _next;QDataType _data;
}QueueNode;
typedef struct Queue//队列的结构
{QueueNode* _head;//头指针QueueNode* _tail;//尾指针
}Queue;void QueueInit(Queue* qu);//初始化栈void QueueDestory(Queue* qu);//摧毁栈void QueuePush(Queue* qu,QDataType data);//入队void QueuePop(Queue* qu);//出队QDataType QueueFront(Queue* qu);//返回队头元素
QDataType QueueBack(Queue* qu);//返回队尾元素size_t QueueSize(Queue* qu);//队列长度bool QueueEmpty(Queue* qu);//判断队列是否为空//Queue.c
#include"Queue.h"
void QueueInit(Queue* qu)//初始化栈
{qu->_head = qu->_tail = NULL;
}
void QueueDestory(Queue* qu)//摧毁栈
{//确保指针有效assert(qu);QueueNode* cur = qu->_head;while (cur){QueueNode* next = cur->_next;free(cur);}
}
void QueuePush(Queue* qu,QDataType data)//入队
{if (qu->_head == NULL){qu->_head = (QueueNode*)malloc(sizeof(QueueNode));qu->_tail = qu->_head;qu->_head->_next = NULL;qu->_head->_data = data;}else{//尾部入数据QueueNode* cur = qu->_tail;QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));cur->_next = newNode;newNode->_next = NULL;qu->_tail = newNode;newNode->_data = data;}
}
void QueuePop(Queue* qu)//出队
{//队头出数据QueueNode* head = qu->_head;qu->_head = head->_next;free(head);
}
QDataType QueueFront(Queue* qu)//返回队头元素
{return qu->_head->_data;
}
QDataType QueueBack(Queue* qu)//返回队尾元素
{return qu->_tail->_data;
}
size_t QueueSize(Queue* qu)//队列长度
{assert(qu);//确保指针存在QueueNode* cur = qu->_head;size_t size = 0;while (cur){++size;cur = cur->_next;}return size;
}
bool QueueEmpty(Queue* qu)//判断队列是否为空
{return !qu->_head;
}//Test.c
#include"BTree.h"
void TestBTreeNode()
{BTreeNode* root = NULL;root = CreatBinaryTree(root);/*PreOrder(root);printf("\n");InOrder(root);printf("\n");PostOrder(root);*///printf("%d\n", BinaryTreeSize(root));printf("%d\n", BinaryTreeLeafSize(root));printf("%d\n", BinarTreelen(root));//LevelOrder(root);printf("%d\n", BinaryTreeComplete(root));printf("%d\n", BinaryTreeLevelKSize(root, 3));BinaryTreeDestory(root);root = NULL;//根节点置空,防止野指针的问题
}
int main()
{TestBTreeNode();}相关文章:

二叉树的介绍及二叉树的链式结构的实现(C语言版)
前言 二叉树是一种特殊的树,它最大的度为2,每个节点至多只有两个子树。它是一种基础的数据结构,后面很多重要的数据结构都是依靠它来进行实现的。了解并且掌握它是很重要的。 目录 1.二叉树的介绍 1.1概念 1.2现实中的二叉树 1.3特殊的二叉…...
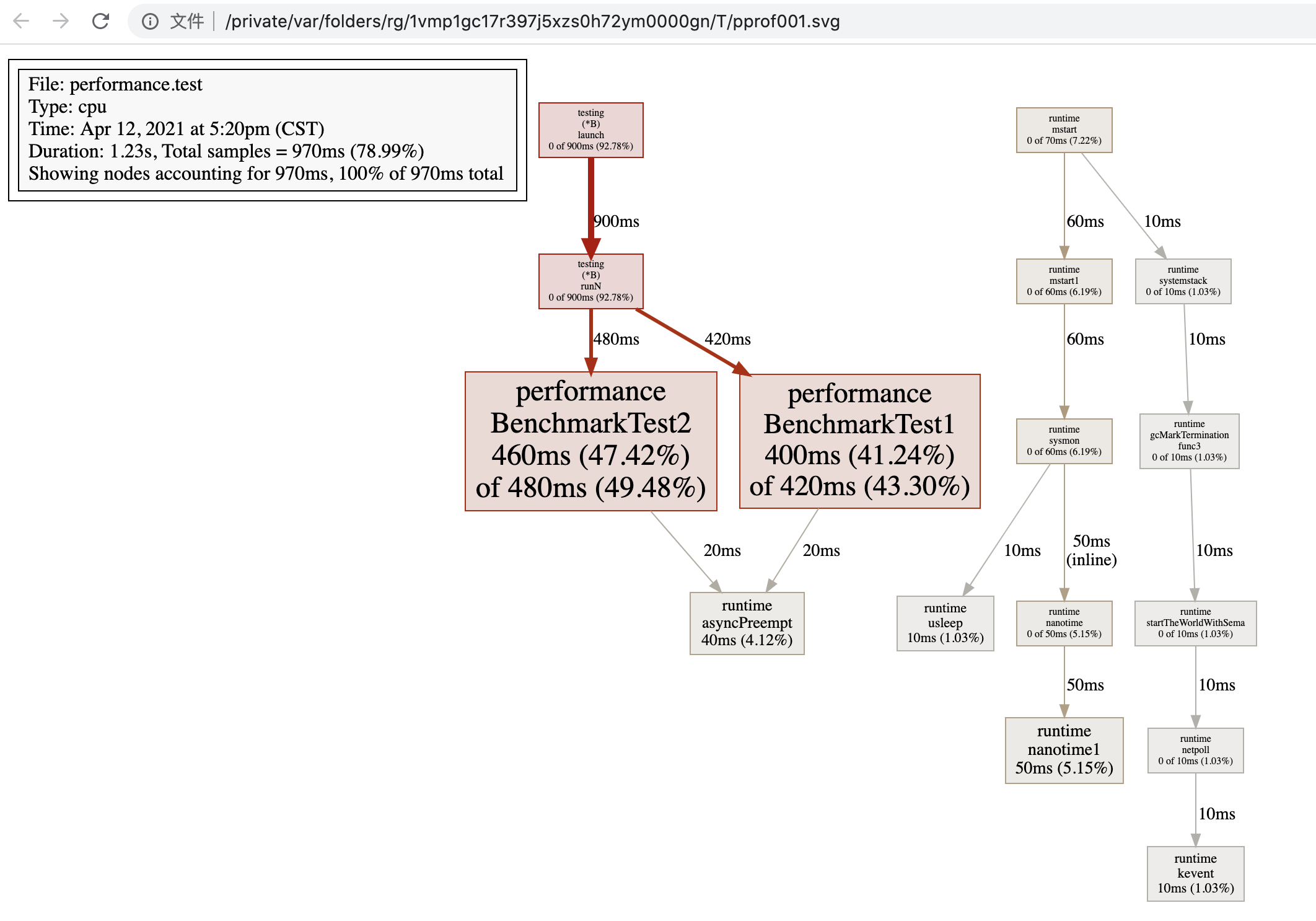
不同写法的性能差异
“ 达到相同目的,可以有多种写法,每种写法有性能、可读性方面的区别,本文旨在探讨不同写法之间的性能差异 len(str) vs str "" 本部分参考自: [问个 Go 问题,字符串 len 0 和 字符串 "" ,有啥区别?](https://segmentf…...

Bytebase 2.7.0 - 新增分支(Branching)功能
🚀 新功能 新增支持与 Git 类似的分支(Branching)功能来管理 schema 变更。支持搜索所有历史工单。支持导出审计日志。 🎄 改进 变更数据库工单详情页面全新改版。优化工单搜索体验。SQL 审核规则支持针对不同数据库进行独立配…...

day55 动规.p15 子序列
- 392.判断子序列 cpp class Solution { public: bool isSubsequence(string s, string t) { vector<vector<int>> dp(s.size() 1, vector<int>(t.size() 1, 0)); for (int i 1; i < s.size(); i) { for (int j 1; …...

TypeScript DOM类型的声明
TS DOM类型的声明 lib.dom.d.ts HTMLInputElement <input type"text" change"handleChange" /> const handleChange (evt: Event) > {console.log((evt.target as HTMLInputElement).value); } HTMLElement const div: HTMLDivElement do…...
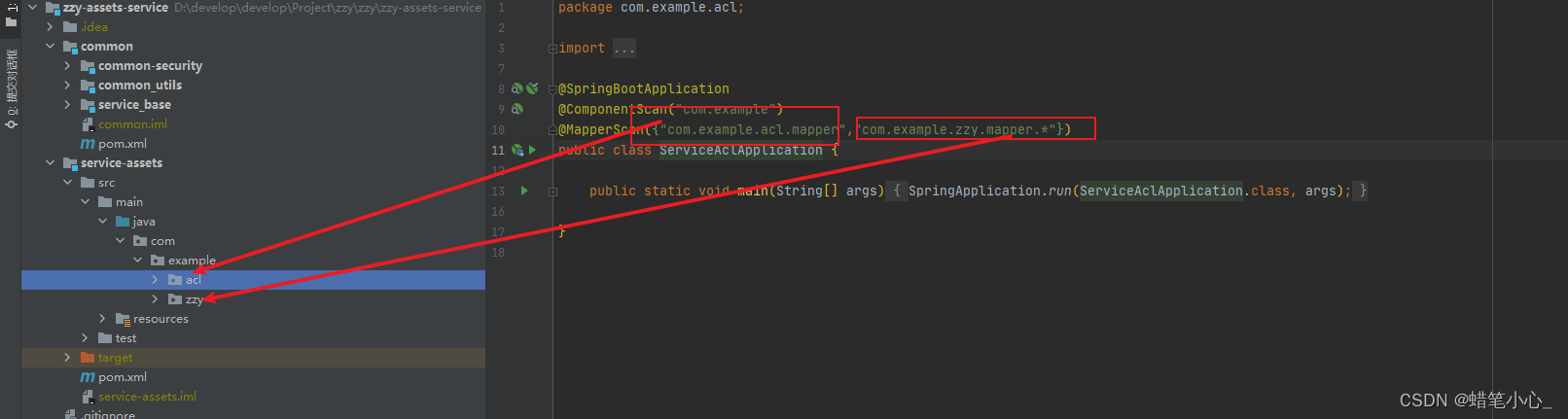
springboot找不到注册的bean
1、错误描述 A component required a bean named ‘fixedAssetsShareMapper’ that could not be found.Action:Consider defining a bean named ‘fixedAssetsShareMapper’ in your configuration.2、问题分析 1、该错误提示表明在你的应用程序中有一个组件(可能…...
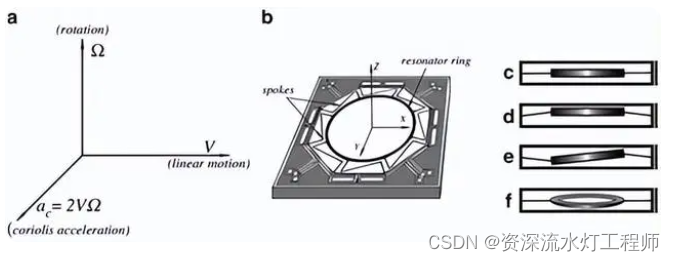
MEMS传感器的原理与构造——单片式硅陀螺仪
一、前言 机械转子式陀螺仪在很长的一段时间内都是唯一的选项,也正是因为它的结构和原理,使其不再适用于现代小型、单体、集成式传感器的设计。常规的机械转子式陀螺仪包括平衡环、支撑轴承、电机和转子等部件,这些部件需要精密加工和…...
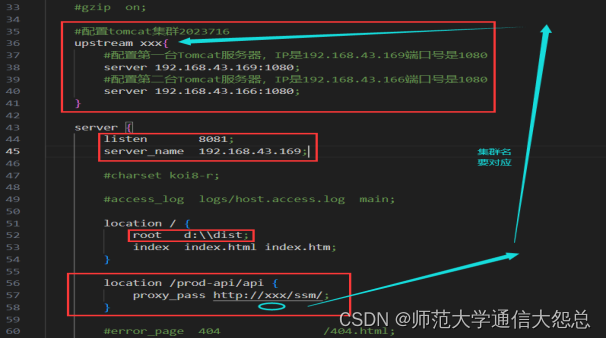
Redis集群服务器
集群简介 试想有一家餐厅,如果顾客人数较少,那么餐厅只需要一个服务员即可,如图1。但是,当顾客人数非常多时,一个服务员是绝对不够的,如图2。此时,餐厅需要雇用更多的服务员来解决大量访问&…...

动态维护直径 || 动态维护树上路径 || 涉及LCA点转序列 || 对欧拉环游序用数据结构维护:1192B
https://www.luogu.com.cn/problem/CF1192B 对于直径的求法,常用dp或两次dfs,但如果要动态维护似乎都不太方面,那么可以维护树上路径最大值。 树上路径为: d e p u d e p v − 2 d e p l c a ( u , v ) dep_udep_v-2\times de…...
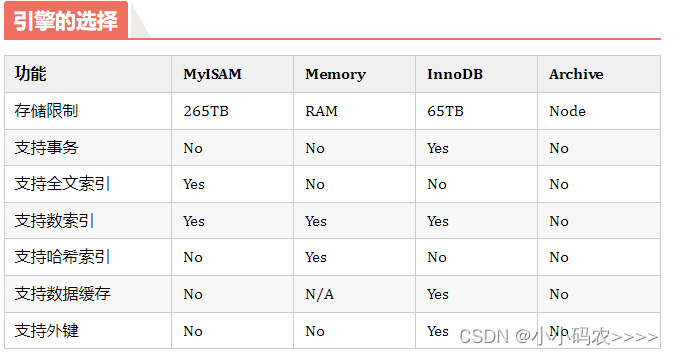
MySQL 存储引擎,你了解几个?
引言 MySQL是一种流行的关系型数据库管理系统(RDBMS),它支持多种不同的数据库引擎。数据库引擎是用于存储、管理和检索数据的核心组件,它们直接影响着数据库的性能、可靠性和功能,接下来本文介绍下一些常见的MySQL数据…...

Java 动态规划 Leetcode 740. 删除并获得点数
题目 对于该题的题目分析,已经代码分析都一并写入到了代码注释中 代码 class Solution {public int deleteAndEarn(int[] nums) {//核心思路://由于我们获得 nums[i] 的点数之后,就必须删除所有等于 nums[i] - 1 和 nums[i] 1 的元素//假设…...

算法通关村十三关-青铜:数字与数学基础问题
1.数字统计专题 统计特定场景下的符号或数字个数等 1.1符号统计 LeetCode1822 数组元素积的符号 https://leetcode.cn/problems/sign-of-the-product-of-an-array/description/ 思路分析 如果将所有的数都乘起来,再判断正负,工作量大,还…...
猜拳游戏小程序源码 大转盘积分游戏小程序源码 积分游戏小程序源码
简介: 猜拳游戏大转盘积分游戏小程序前端模板源码,一共五个静态页面,首页、任务列表、大转盘和猜拳等五个页面 图片:...

【Python】爬虫练习-爬取豆瓣网电影评论用户的观影习惯数据
目录 前言 一、配置环境 1.1、 安装Python 1.2、 安装Requests库和BeautifulSoup库 1.3.、安装Matplotlib 二、登录豆瓣网(重点) 2.1、获取代理 2.2、测试代理ip是否可用 2.3、设置大量请求头随机使用 2.4、登录豆瓣网 三、爬取某一部热门电影…...

webpack基础配置【总结】
webpack打包原理: webpack是一个js应用程序的静态模块打包工具,当webpack处理应用程序时,它的内部构建一个依赖图,此时依赖会映射项目中所需的每个模块,并生成一个或多个bundle包。因此我们会安装配置各种打包规则&…...

typescript 支持与本地调试
typescript 支持与本地调试 typescript 支持与本地调试 前言支持 typescript函数的本地调试 启用 node-terminal 调试invoke localserverless-offline Next Chapter完整示例及文章仓库地址 前言 在上一章节,我们创建了一个 hello world 函数,并把它顺…...

后端面试话术集锦第 十八 篇:JVM面试话术
这是后端面试集锦第十八篇博文——JVM面试话术❗❗❗ 1. 介绍下JVM JVM主要包括:类加载器(class loader)、执行引擎(exection engine)、本地接口(native interface)、运行时数据区(Runtimedata area) 类加载器:加载类文件到内存。Class loader只管加载,只要符合文件…...

“历久弥新 | 用AI修复亚运珍贵史料”活动震撼来袭!
时隔近半个世纪,新中国第一次参与亚运会的影像资料将首次对外披露。只是年代久远,老照片老视频都有了岁月痕迹,画面不再清晰,这些珍贵史料急需你的帮助! 一、活动介绍 2023年,正值亚运110周年,…...

uni-app 之 scroll-view和swiper
uni-app 之 scroll-view和swiper <!-- vue2的<template>里必须要有一个盒子,不能有两个,这里的盒子就是 view--> <template><view><navigator url"/pages/home/home"><button style"background: #ff00f…...

Harmony网络请求工具类
使用的网络请求框架是axios 1、安装axios ohpm install @ohos/axios2、封装 import axios, { FormData } from "@ohos/axios" import fs from @ohos.file.fs import ArrayList from @ohos.util.ArrayList/*** 网络请求工具类*/ class HttpManager {baseUrl:string…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
