较难的换根dp:P6213 「SWTR-04」Collecting Coins
传送门
前题提要:感觉这道换根dp可以说是集中了换根dp的所有较高难度的操作和思想,以及较高的一些实现细节,可以说能够完全写出这道题才叫真正理解了换根dp,非常值得一做.
首先读完题意,不难发现这道题有很多限制.点的访问次数限制,必须访问某一个点,想要获得最大的贡献,没有限制初始起点.乍一看感觉完全没办法解决,我们考虑一个一个的去解决上述限制.
首先假设只想获得最大的贡献,那么这个显然是一个简单的树形dp,也就是 f [ u ] = m a x ( f [ v ] + w ) f[u]=max(f[v]+w) f[u]=max(f[v]+w). f [ u ] f[u] f[u]表示访问 u u u子树所能获得的最大贡献.
然后我们考虑加上访问次数的限制,我们发现对于一个点,无论他是起始点还是中途经过的点,只要访问这个点,我们就损失了一个进入机会.然后显然我们想访问一个子树获得子树的贡献就需要花费一次进入机会,因为我们进入一个子树必然需要返回.诶,此时我们就可以解决了.假设一个点的访问次数限制为 k k k,那么对于这个点来说,我们最多只能加入 k − 1 k-1 k−1个子树的贡献.所以我们考虑对所有子树的贡献进行一个排序,然后取前 k − 1 k-1 k−1个最大的贡献即可.
然后我们再考虑加入必须访问一个点的贡献.这一点直接解决起来就有点困难了,我们需要转化一下这个条件.我们考虑将这个必须访问的点当做我们的遍历的树的根节点,这样我们的必须访问的需求就迎刃而解了.因为对于刚开始的一棵树来说,我们这个根节点是必须遍历的,没有任何问题.
然后因为本题并没有限制初始点,所以我们需要进行一个换根.那么对于换完根的树来说,因为存在一个必须访问的点,所以我们限制换完根的子树必须选祖先那个子树即可.然后在自己的子树里选出前 k − 2 k-2 k−2大的.
至此本题的主要解决思路就结束了,但是本题在换根上的细节和经验问题还是比较多的(反正我当时在写这道题被细节方面搞了很久),接下来详细讲讲细节方面的处理
其实建议不看下文自己解决细节问题,毕竟只有自己的连续思考才毕竟清楚
考虑我们维护出了 f [ u ] f[u] f[u]表示访问一个节点所能获得的最大贡献,并且因为换根需求,我们考虑记录使用 m a x _ f max\_f max_f记录下所有的u子树对u的贡献,并且对此从大到小排个序.
PS:这种记录子树对u的贡献的方法在很多题目中都需要体现(因为换根的时候需要考虑自身节点对父亲的贡献),但是很多题目都是记录最大值和次大值即可,这样较为方便,但是实际上那些题目都是可以直接记录所有的贡献然后等会处理,并且在本题中光记录最大和次大并不能解决问题,所以考虑直接记录所有的贡献
因为我们的父亲节点是必选的,为了方便解决问题,不妨设置一个辅助数组 f a _ v a l [ u ] fa\_val[u] fa_val[u]来记录以 u u u为根时 u u u节点的父亲子树对 u u u的贡献.然后设 d p [ u ] dp[u] dp[u]记录以 u u u为根时的贡献.
先来维护 f a _ v a l [ u ] fa\_val[u] fa_val[u]数组
然后我们考虑根节点从 u − > v u->v u−>v转移,此时需要进行分类讨论,考虑先维护辅助数组:
- 当v子树是 f [ u ] f[u] f[u]数组的一个贡献来源时:此时我们想要维护 f a _ v a l [ u ] fa\_val[u] fa_val[u]时,我们需要花费一次进入机会从 v v v进入到 u u u,然后我们还需要一次进入机会从 u u u到 u u u的父亲节点(因为父亲节点是必选的),所以此时我们就只剩下 k − 2 k-2 k−2棵可选择的子树贡献(并且这个k-2可子树是不能包括v的),那么考虑预处理出原本 u u u子树原 k − 1 k-1 k−1课子树的总贡献,然后减掉 v v v这个子树的贡献就维护出了前 k − 2 k-2 k−2棵除v子树外的最大贡献了.但是光光这样的方式是有问题的(当时卡了我很长时间),因为假设我们的u是根节点时,我们此时没有父亲那边的贡献,并且我们也不需要花一次进入机会去进入到父亲节点,所以这种情况下是需要特判的,具体特判方式看下文代码即可,此处不在赘述
- 考虑v子树不是 f [ u ] f[u] f[u]的一个贡献来源,那么此时我们想要维护 f a _ v a l [ u ] fa\_val[u] fa_val[u]时,我们同样此时只需要记录 u u u子树除 v v v外的前 k − 2 k-2 k−2棵子树的贡献即可.因为此时v不处于前 k − 1 k-1 k−1大的贡献之间,所以我们直接预处理前 k − 2 k-2 k−2的 m a x _ f max\_f max_f的和即可.同样的,当我们是处于根节点时照样需要特判.
考虑我们如果维护出了 f a _ v a l fa\_val fa_val数组之后,对于我们的 d p dp dp数组就不难维护了,我们此时的 d p [ u ] = f a _ v a l [ u ] + u 前 k − 2 大的子树的贡献和 dp[u]=fa\_val[u]+u前k-2大的子树的贡献和 dp[u]=fa_val[u]+u前k−2大的子树的贡献和
PS:此处同时也有一个小trick,因为时间复杂度的约束,我们不能实时的枚举v是否是u的一个贡献子树,所以我们需要在遍历子树之前先预处理一下这个状态,并且同时记录下前k-1大,前k大,前k-2大的子树的贡献和即可
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
inline void print(__int128 x){if(x<0) {putchar('-');x=-x;}if(x>9) print(x/10);putchar(x%10+'0');
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Edge{int v,w;
};
vector<Edge>edge[maxn];int k[maxn];
int f[maxn];vector<pair<int,int> >max_f[maxn];
int n,d;
void dfs1(int u,int per_u) {for(auto [v,w]:edge[u]) {if(v==per_u) continue;dfs1(v,u);max_f[u].push_back({f[v]+w,v});}sort(max_f[u].begin(),max_f[u].end());reverse(max_f[u].begin(),max_f[u].end());for(int i=0;i<min((int)max_f[u].size(),k[u]-1);i++) {f[u]+=max_f[u][i].first;}
}
int dp[maxn];int check[maxn];int fa_val[maxn];
void dfs2(int u,int per_u) {int sum1=0,sum2=0,sum3=0;for(int i=0;i<max_f[u].size();i++) {int v=max_f[u][i].second;int w=max_f[u][i].first;if(i<k[u]-1) sum1+=w,check[v]=1;if(i<k[u]) sum2+=w;if(i<k[u]-2) sum3+=w;}dp[u]+=sum3;for(auto [v,w]:edge[u]) {if(v==per_u) continue;if(k[v]==1) continue;if(check[v]) {if(u!=d) fa_val[v]=fa_val[u]+sum1-f[v]-w+w;else fa_val[v]=fa_val[u]+sum2-f[v]-w+w; dp[v]=fa_val[v];}else {if(u!=d) fa_val[v]=fa_val[u]+sum3+w;else fa_val[v]=fa_val[u]+sum1+w; dp[v]=fa_val[v];} dfs2(v,u);}
}
int main() {n=read();d=read();for(int i=1;i<n;i++) {int u=read();int v=read();int w=read();edge[u].push_back({v,w});edge[v].push_back({u,w});}for(int i=1;i<=n;i++) {k[i]=read();}dfs1(d,0);dfs2(d,0);int ans=f[d];for(int i=1;i<=n;i++) {ans=max(ans,dp[i]);}cout<<ans<<endl;return 0;
}
相关文章:

较难的换根dp:P6213 「SWTR-04」Collecting Coins
传送门 前题提要:感觉这道换根dp可以说是集中了换根dp的所有较高难度的操作和思想,以及较高的一些实现细节,可以说能够完全写出这道题才叫真正理解了换根dp,非常值得一做. 首先读完题意,不难发现这道题有很多限制.点的访问次数限制,必须访问某一个点,想要获得最大的贡献,没有…...

Springboot - 15.二级分布式缓存集成-Caffeine
👀中文文档 Caffeine 👀使用Caffeine (本地缓存) 当与Spring Boot结合使用时,Caffeine提供了一个直观且功能强大的二级缓存解决方案。Spring Boot的缓存抽象使得整合Caffeine变得相当简单。以下是如何在Spring Boot…...
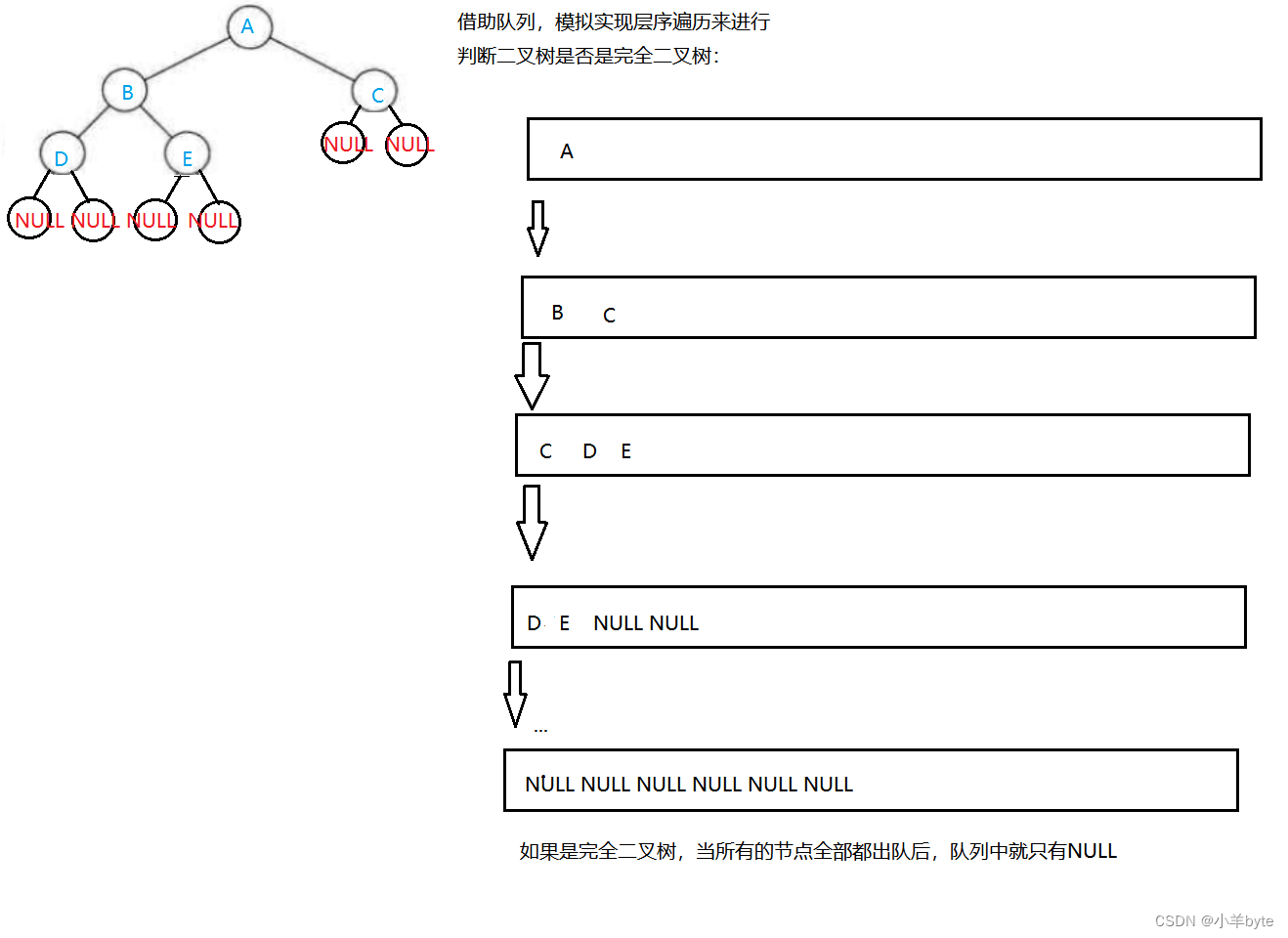
二叉树的介绍及二叉树的链式结构的实现(C语言版)
前言 二叉树是一种特殊的树,它最大的度为2,每个节点至多只有两个子树。它是一种基础的数据结构,后面很多重要的数据结构都是依靠它来进行实现的。了解并且掌握它是很重要的。 目录 1.二叉树的介绍 1.1概念 1.2现实中的二叉树 1.3特殊的二叉…...
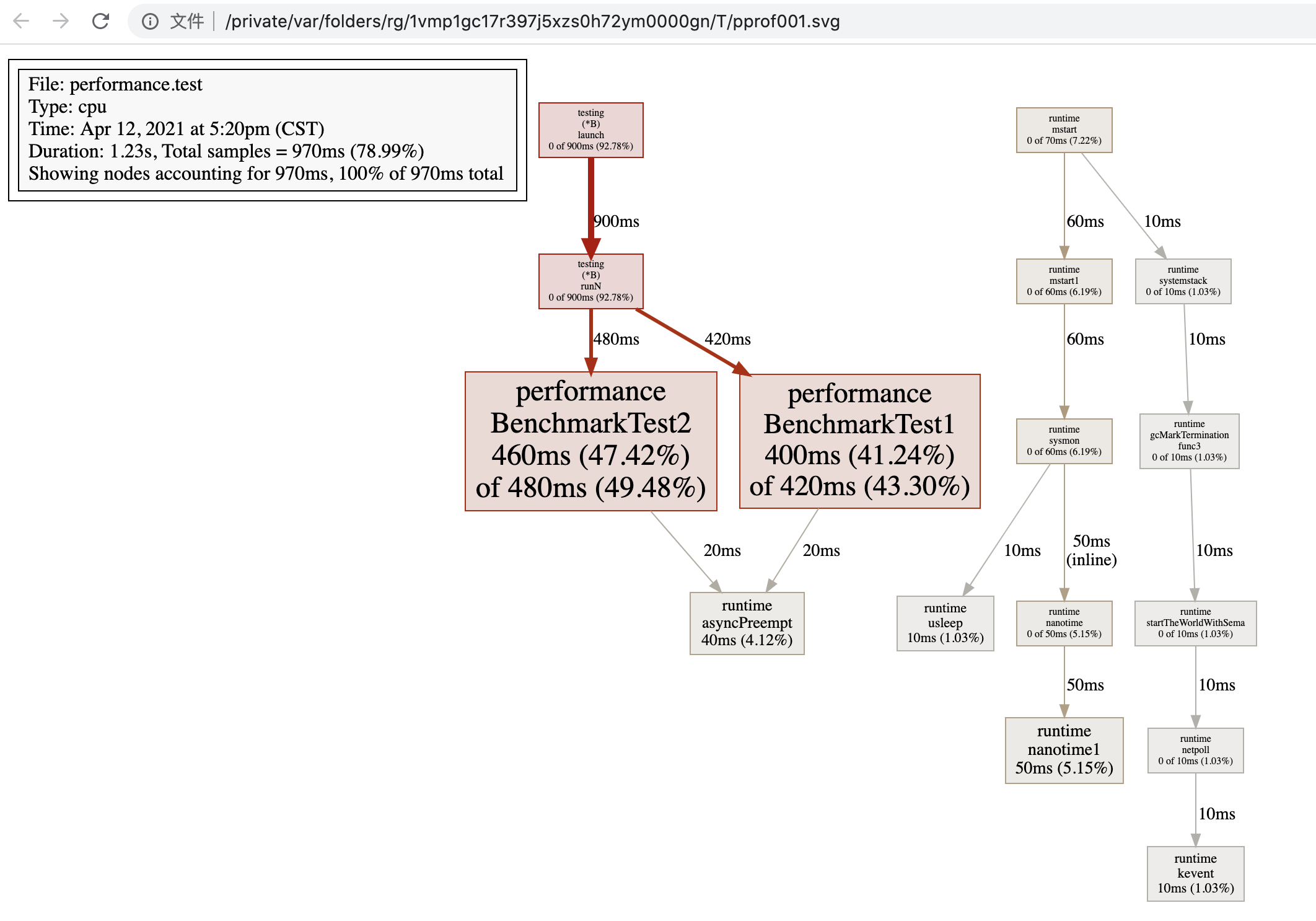
不同写法的性能差异
“ 达到相同目的,可以有多种写法,每种写法有性能、可读性方面的区别,本文旨在探讨不同写法之间的性能差异 len(str) vs str "" 本部分参考自: [问个 Go 问题,字符串 len 0 和 字符串 "" ,有啥区别?](https://segmentf…...

Bytebase 2.7.0 - 新增分支(Branching)功能
🚀 新功能 新增支持与 Git 类似的分支(Branching)功能来管理 schema 变更。支持搜索所有历史工单。支持导出审计日志。 🎄 改进 变更数据库工单详情页面全新改版。优化工单搜索体验。SQL 审核规则支持针对不同数据库进行独立配…...

day55 动规.p15 子序列
- 392.判断子序列 cpp class Solution { public: bool isSubsequence(string s, string t) { vector<vector<int>> dp(s.size() 1, vector<int>(t.size() 1, 0)); for (int i 1; i < s.size(); i) { for (int j 1; …...

TypeScript DOM类型的声明
TS DOM类型的声明 lib.dom.d.ts HTMLInputElement <input type"text" change"handleChange" /> const handleChange (evt: Event) > {console.log((evt.target as HTMLInputElement).value); } HTMLElement const div: HTMLDivElement do…...
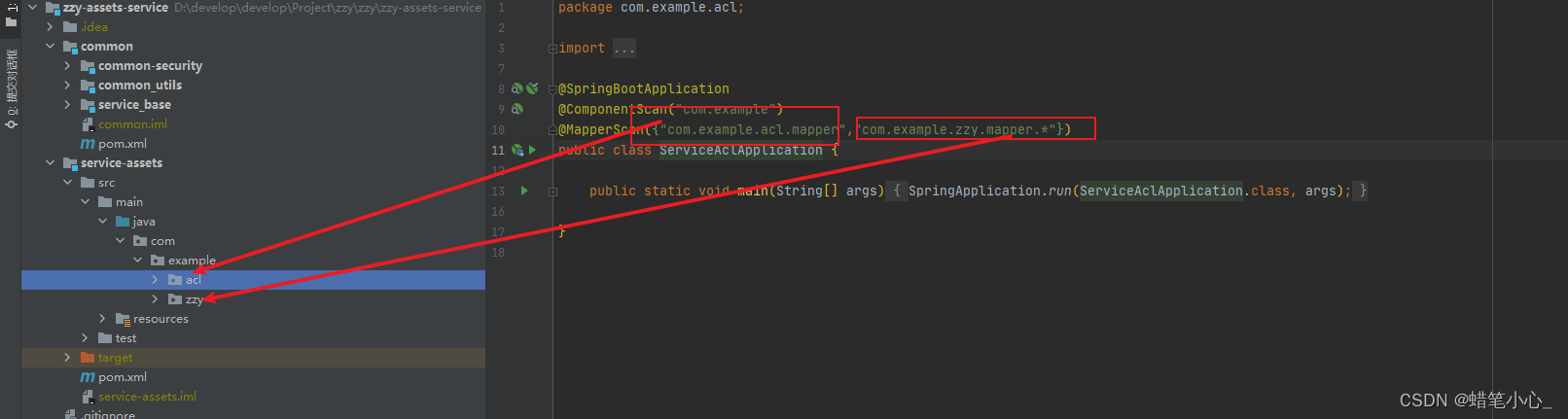
springboot找不到注册的bean
1、错误描述 A component required a bean named ‘fixedAssetsShareMapper’ that could not be found.Action:Consider defining a bean named ‘fixedAssetsShareMapper’ in your configuration.2、问题分析 1、该错误提示表明在你的应用程序中有一个组件(可能…...
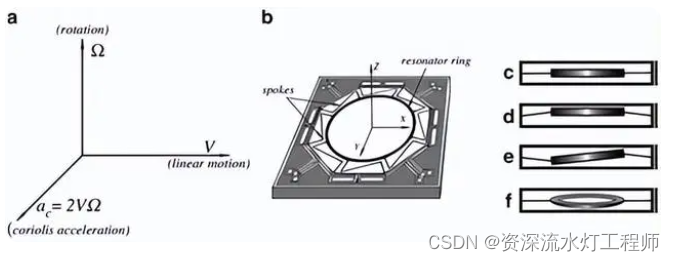
MEMS传感器的原理与构造——单片式硅陀螺仪
一、前言 机械转子式陀螺仪在很长的一段时间内都是唯一的选项,也正是因为它的结构和原理,使其不再适用于现代小型、单体、集成式传感器的设计。常规的机械转子式陀螺仪包括平衡环、支撑轴承、电机和转子等部件,这些部件需要精密加工和…...
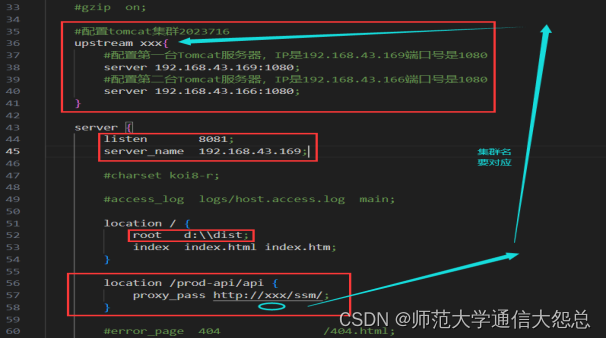
Redis集群服务器
集群简介 试想有一家餐厅,如果顾客人数较少,那么餐厅只需要一个服务员即可,如图1。但是,当顾客人数非常多时,一个服务员是绝对不够的,如图2。此时,餐厅需要雇用更多的服务员来解决大量访问&…...

动态维护直径 || 动态维护树上路径 || 涉及LCA点转序列 || 对欧拉环游序用数据结构维护:1192B
https://www.luogu.com.cn/problem/CF1192B 对于直径的求法,常用dp或两次dfs,但如果要动态维护似乎都不太方面,那么可以维护树上路径最大值。 树上路径为: d e p u d e p v − 2 d e p l c a ( u , v ) dep_udep_v-2\times de…...
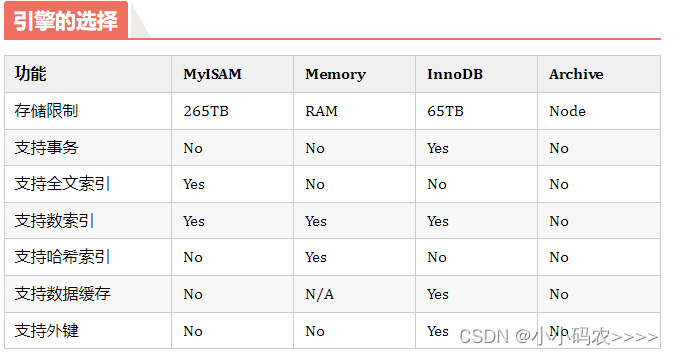
MySQL 存储引擎,你了解几个?
引言 MySQL是一种流行的关系型数据库管理系统(RDBMS),它支持多种不同的数据库引擎。数据库引擎是用于存储、管理和检索数据的核心组件,它们直接影响着数据库的性能、可靠性和功能,接下来本文介绍下一些常见的MySQL数据…...

Java 动态规划 Leetcode 740. 删除并获得点数
题目 对于该题的题目分析,已经代码分析都一并写入到了代码注释中 代码 class Solution {public int deleteAndEarn(int[] nums) {//核心思路://由于我们获得 nums[i] 的点数之后,就必须删除所有等于 nums[i] - 1 和 nums[i] 1 的元素//假设…...

算法通关村十三关-青铜:数字与数学基础问题
1.数字统计专题 统计特定场景下的符号或数字个数等 1.1符号统计 LeetCode1822 数组元素积的符号 https://leetcode.cn/problems/sign-of-the-product-of-an-array/description/ 思路分析 如果将所有的数都乘起来,再判断正负,工作量大,还…...
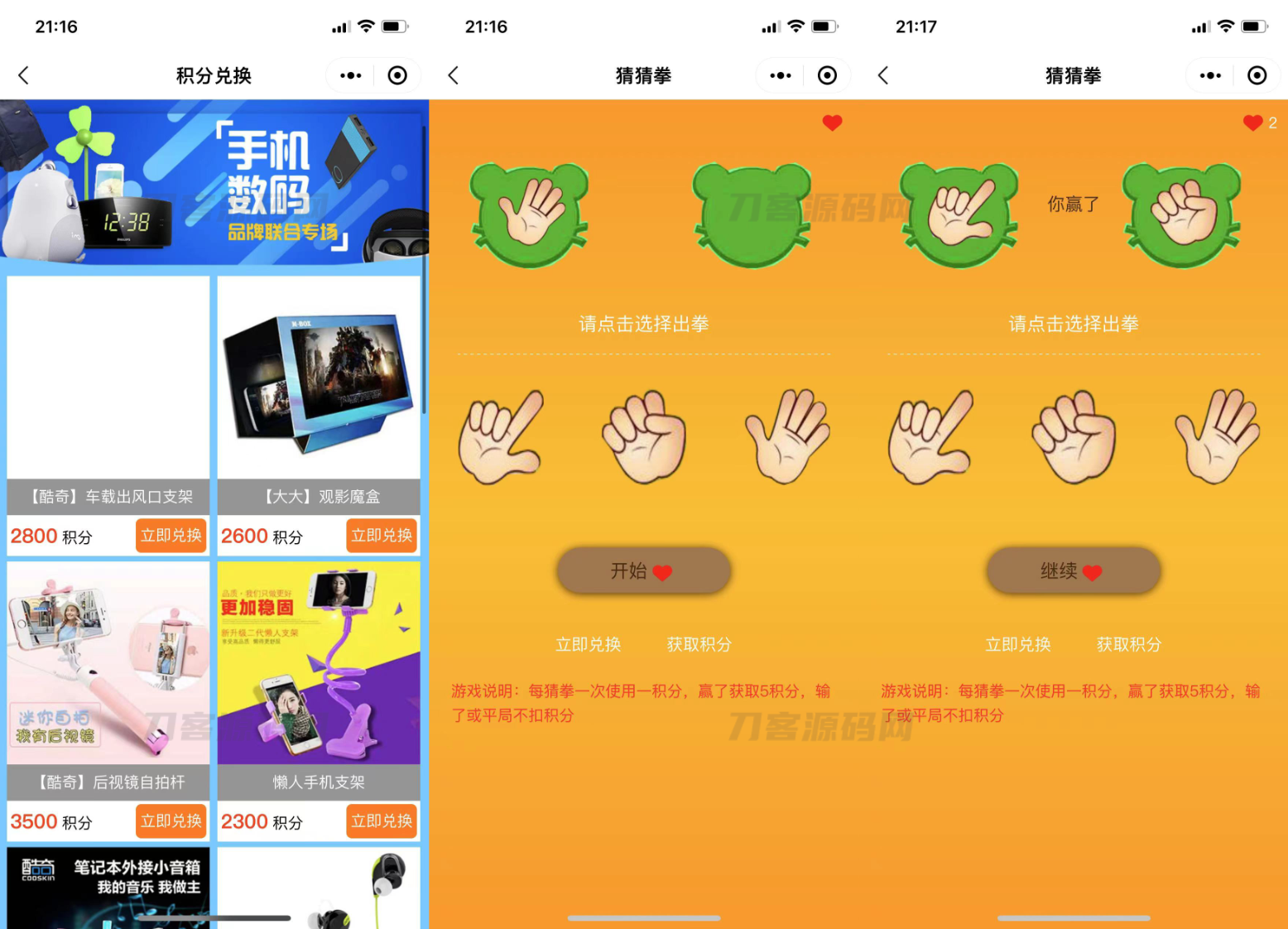
猜拳游戏小程序源码 大转盘积分游戏小程序源码 积分游戏小程序源码
简介: 猜拳游戏大转盘积分游戏小程序前端模板源码,一共五个静态页面,首页、任务列表、大转盘和猜拳等五个页面 图片:...

【Python】爬虫练习-爬取豆瓣网电影评论用户的观影习惯数据
目录 前言 一、配置环境 1.1、 安装Python 1.2、 安装Requests库和BeautifulSoup库 1.3.、安装Matplotlib 二、登录豆瓣网(重点) 2.1、获取代理 2.2、测试代理ip是否可用 2.3、设置大量请求头随机使用 2.4、登录豆瓣网 三、爬取某一部热门电影…...

webpack基础配置【总结】
webpack打包原理: webpack是一个js应用程序的静态模块打包工具,当webpack处理应用程序时,它的内部构建一个依赖图,此时依赖会映射项目中所需的每个模块,并生成一个或多个bundle包。因此我们会安装配置各种打包规则&…...

typescript 支持与本地调试
typescript 支持与本地调试 typescript 支持与本地调试 前言支持 typescript函数的本地调试 启用 node-terminal 调试invoke localserverless-offline Next Chapter完整示例及文章仓库地址 前言 在上一章节,我们创建了一个 hello world 函数,并把它顺…...

后端面试话术集锦第 十八 篇:JVM面试话术
这是后端面试集锦第十八篇博文——JVM面试话术❗❗❗ 1. 介绍下JVM JVM主要包括:类加载器(class loader)、执行引擎(exection engine)、本地接口(native interface)、运行时数据区(Runtimedata area) 类加载器:加载类文件到内存。Class loader只管加载,只要符合文件…...

“历久弥新 | 用AI修复亚运珍贵史料”活动震撼来袭!
时隔近半个世纪,新中国第一次参与亚运会的影像资料将首次对外披露。只是年代久远,老照片老视频都有了岁月痕迹,画面不再清晰,这些珍贵史料急需你的帮助! 一、活动介绍 2023年,正值亚运110周年,…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
