【刷题篇】链表(下)

前言🌸
各位读者们好,本期我们来填填之前留下的坑,继续来讲解几道和链表相关的OJ题。但和上期单向链表不一样的是,我们今天的题目主要是于环形链表有关,下面让我们一起看看吧。
💻本期的题目有:环形链表、环形链表II、求环形链表环长
环形链表💍
a.题目
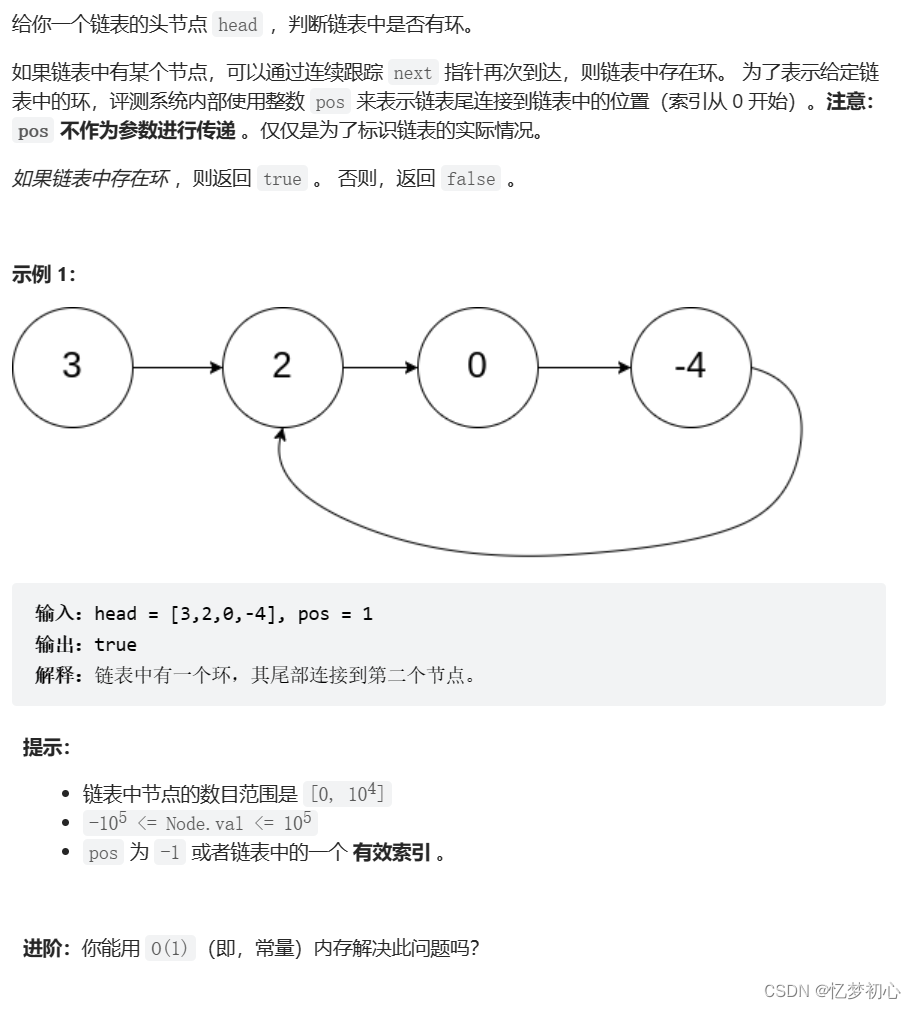
b.题解分析
第一种方法,我们可以遍历链表,使用哈希表来保存已经经过的结点。每次经过一个结点时,通过哈希表判断结点是否被访问过,如果有,则说明存在环;如果没有则继续访问下一结点,以此循环直到遍历完整个链表。这样的时间复杂度为O(N),空间复杂度为O(N),不满足题目的进阶解法。
第二种方法,我们可以使用上期学习的快慢指针法。定义步长为2的快指针和步长为1的慢指针遍历链表。我们假设链表如果存在环,则快慢指针在某一时刻一定会在环内相遇;而如果不存在环,由于快指针速度比慢指针快,因此它们永远无法相遇。动态效果如下:
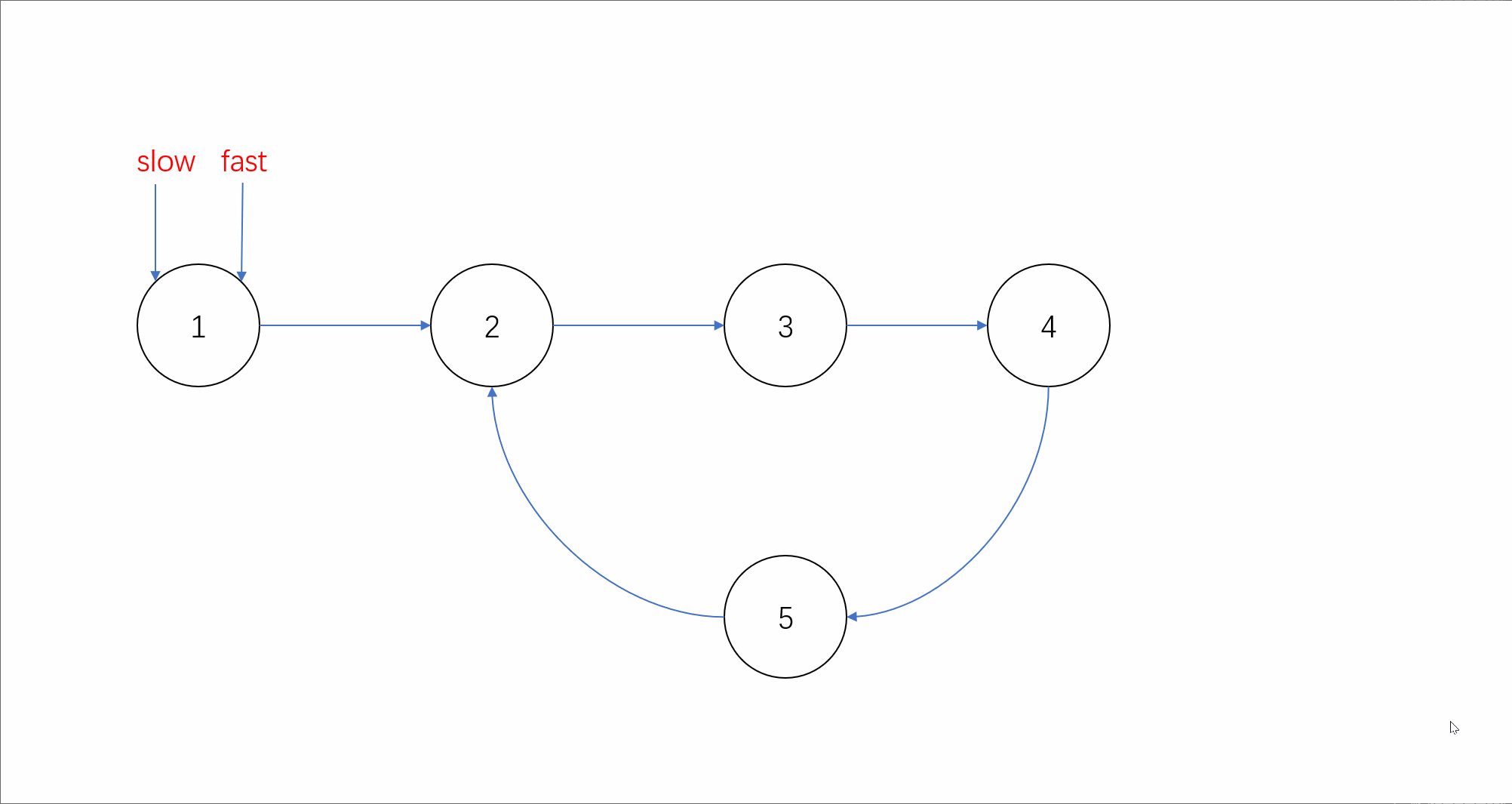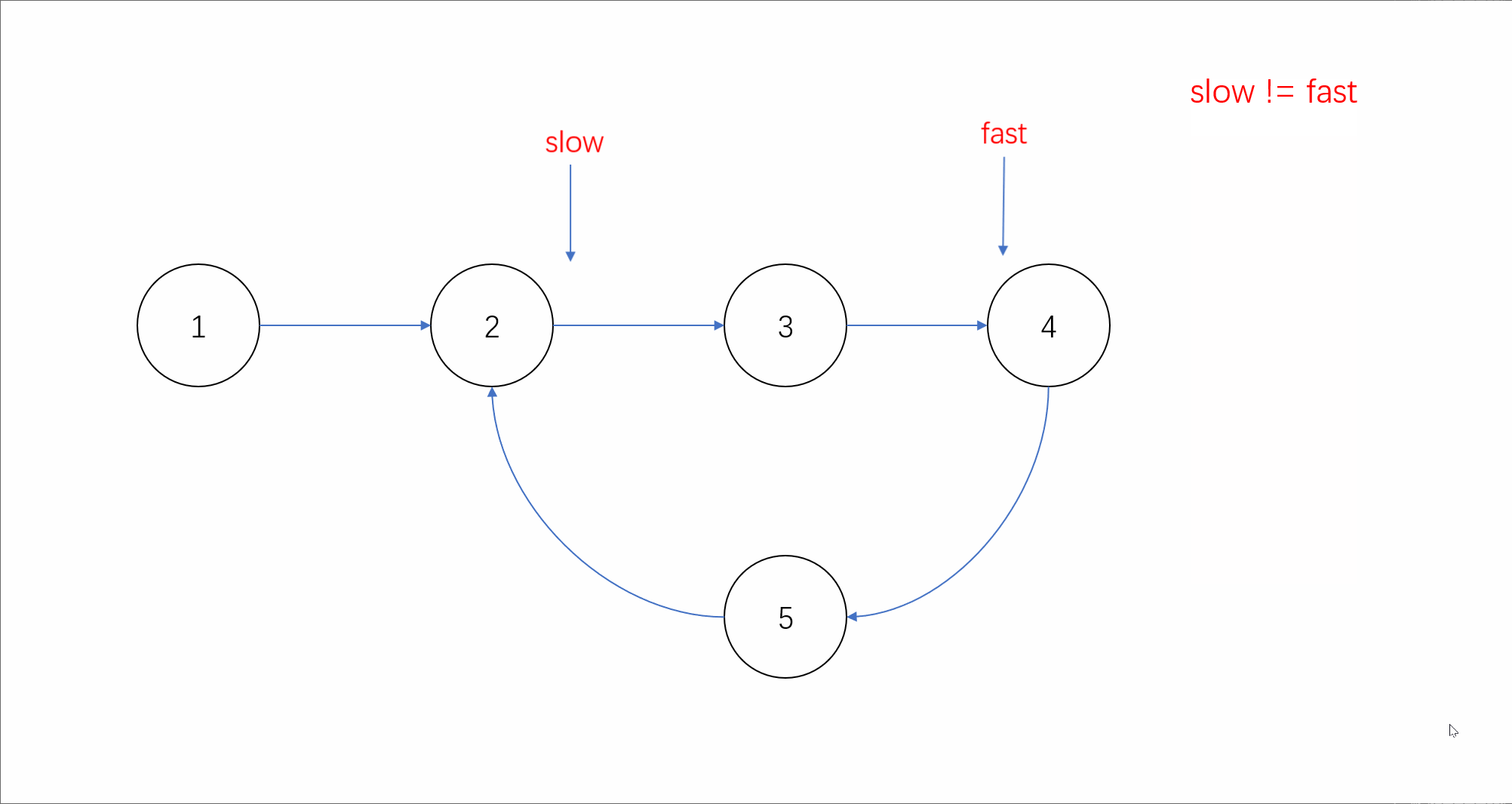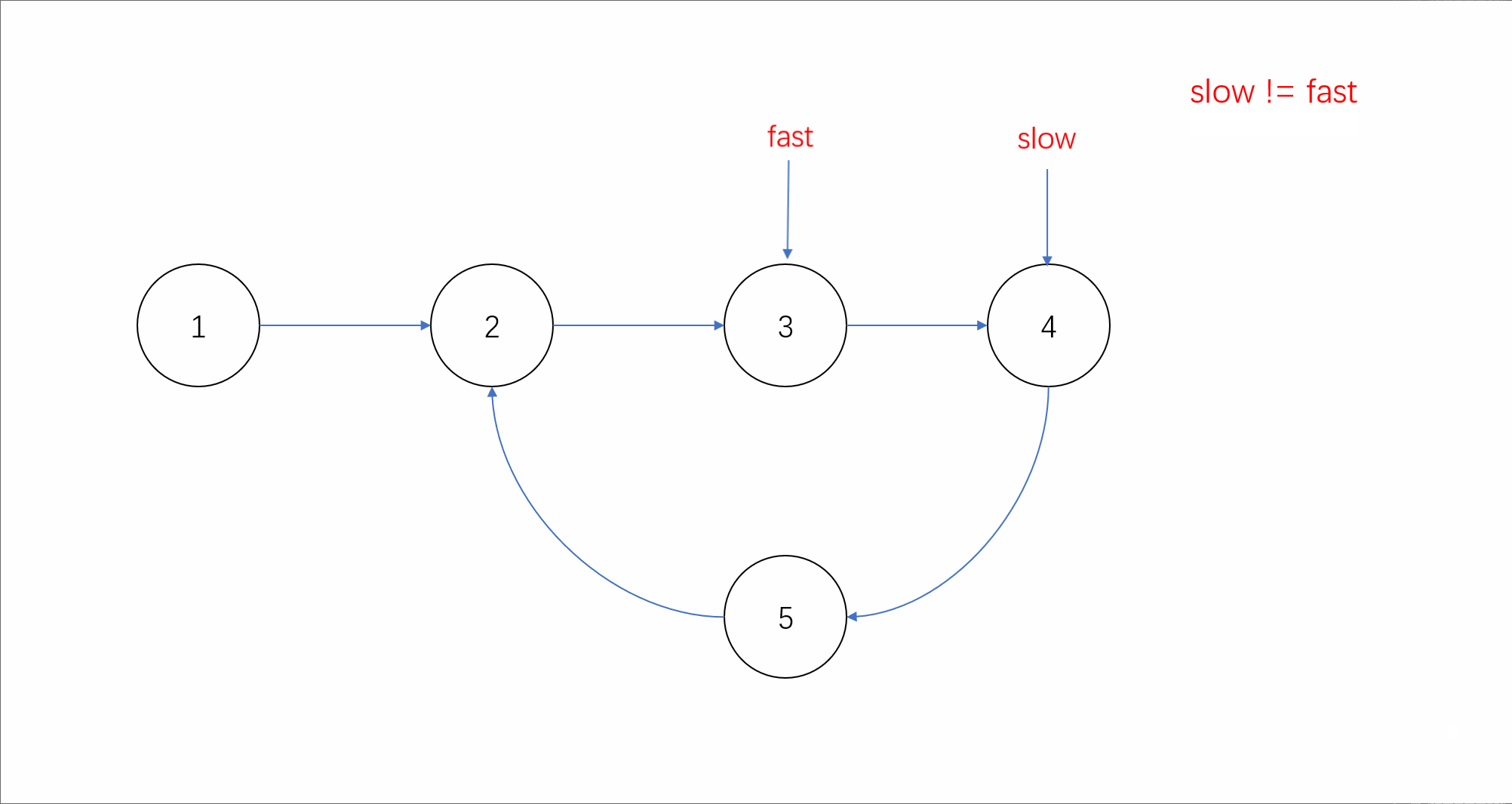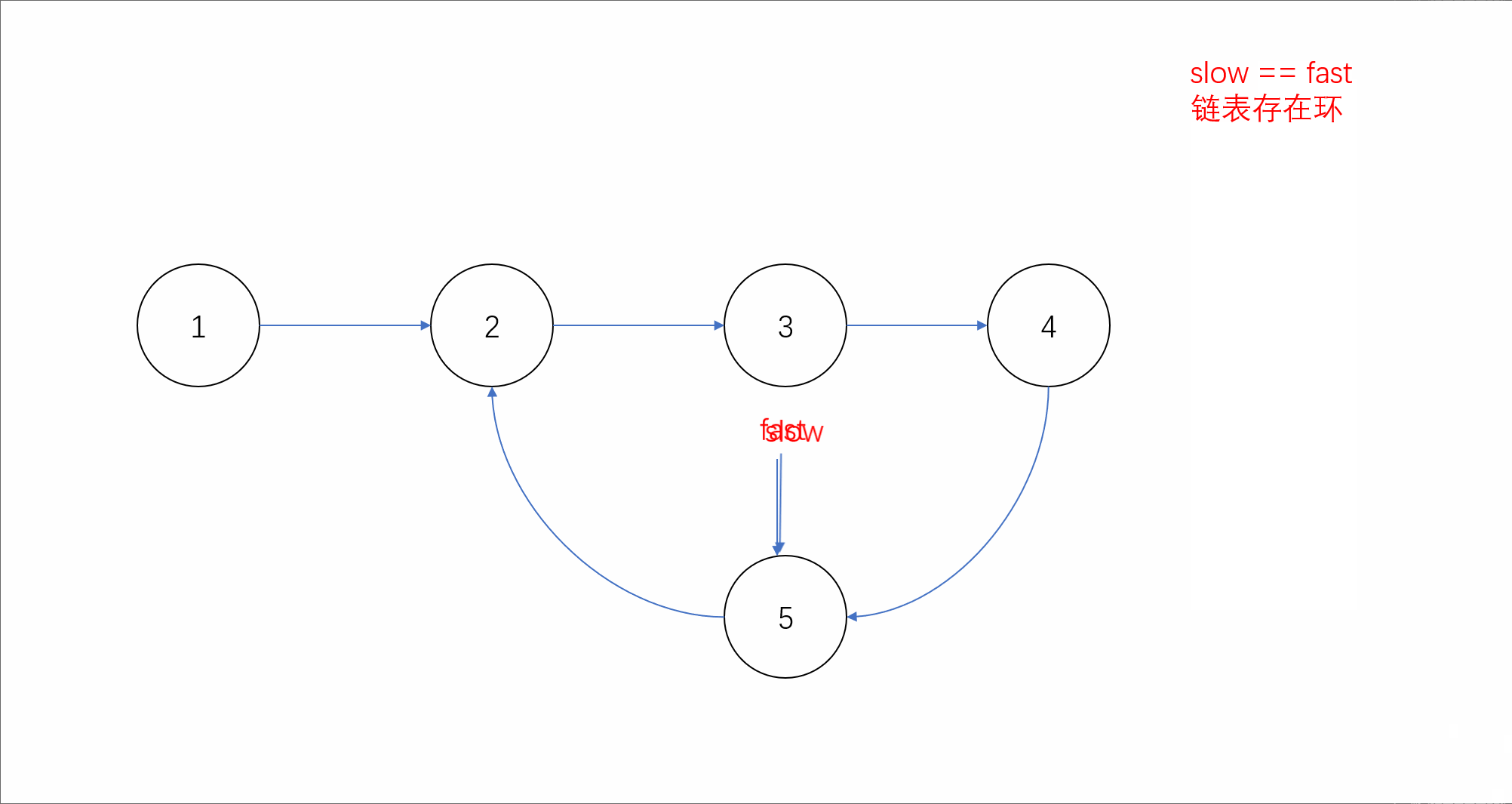
我们可以看到如果链表存在环时,当慢指针进入环中后,快指针就会开始绕环追逐慢指针。我们假设此时快慢指针距离为n,由于v(快)-v(慢)=1,则每次行动快慢指针的距离就会缩短1,行动n次后快慢指针一定就会相遇。因此我们可以通过判断是否相遇来判断是否有环。
c.AC代码
struct ListNode
{int val;struct ListNode* next;
};
bool hasCycle(struct ListNode* head)
{struct ListNode* fast = head;struct ListNode* slow = head;while (fast && fast->next) //当到达或即将到达链表尾时退出循环{//快慢指针移动fast = fast->next->next;slow = slow->next;if (fast == slow){return true; //相遇}}return false; //没有相遇、没有结点、只有一个结点且非循环,不存在环}d.拓展思考
通过以上例子,我们知道速度差为1的快慢指针可以用来判断链表是否存在环。那么,速度差为2的是不是也可以用来判断呢?速度差为3的呢?为n的呢?
我们来分析一下:当快慢指针的速度差为2时,假设慢指针进入环时快指针与其距离为n,环的总长为m,如下:
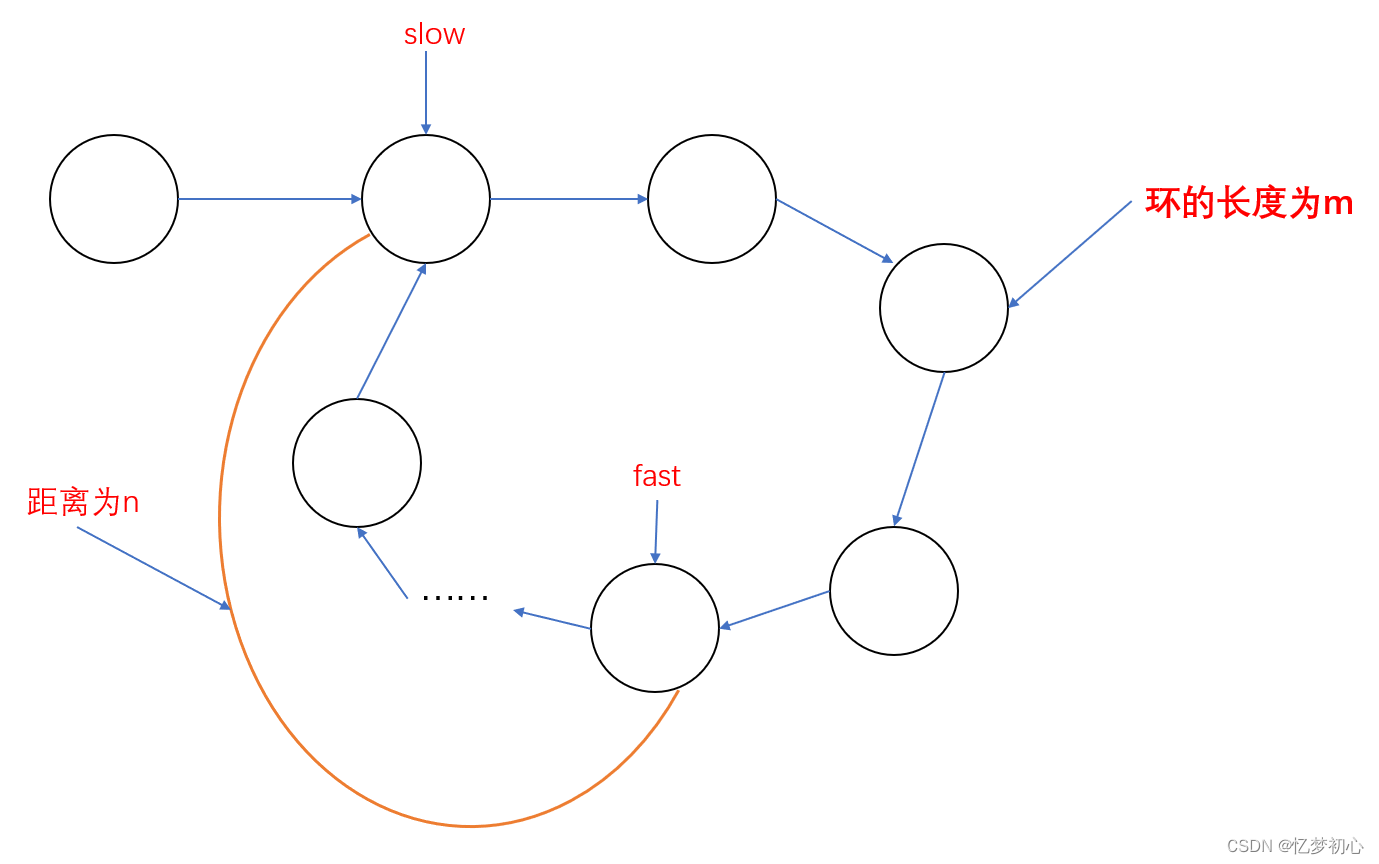
由于它们的速度差为2,则每次行动后n=n-2。我们很容易发现,如果n为偶数时,当行动 次后快慢指针就会相遇;但是当n为奇数时,最后快慢指针就会错过,进入下一轮追赶中。而在第二轮追赶开始时,快慢指针距离为m-1,假如m-1又是奇数,则本轮又会错过进而进入第三轮追逐。然后第三轮开始时依旧相距m-1,又会错过,以此反复......,最后永远不会相遇(史上最遥远的距离,无非就是我在你身旁,你却不理不睬😭)因此,使用速度差为2的快慢指针,不能保证是否可以判断出某个链表是否存在环,速度差为3,为n的同理。
次后快慢指针就会相遇;但是当n为奇数时,最后快慢指针就会错过,进入下一轮追赶中。而在第二轮追赶开始时,快慢指针距离为m-1,假如m-1又是奇数,则本轮又会错过进而进入第三轮追逐。然后第三轮开始时依旧相距m-1,又会错过,以此反复......,最后永远不会相遇(史上最遥远的距离,无非就是我在你身旁,你却不理不睬😭)因此,使用速度差为2的快慢指针,不能保证是否可以判断出某个链表是否存在环,速度差为3,为n的同理。
环形链表 II✈
a.题目

b.题解分析
我们同样可以在上一题的基础上使用快慢指针来求解。
我们假设链表头到环入口的长度为S,环的长度为C。当慢指针走到环入口,此时快指针的位置和慢指针的位置关系如下:
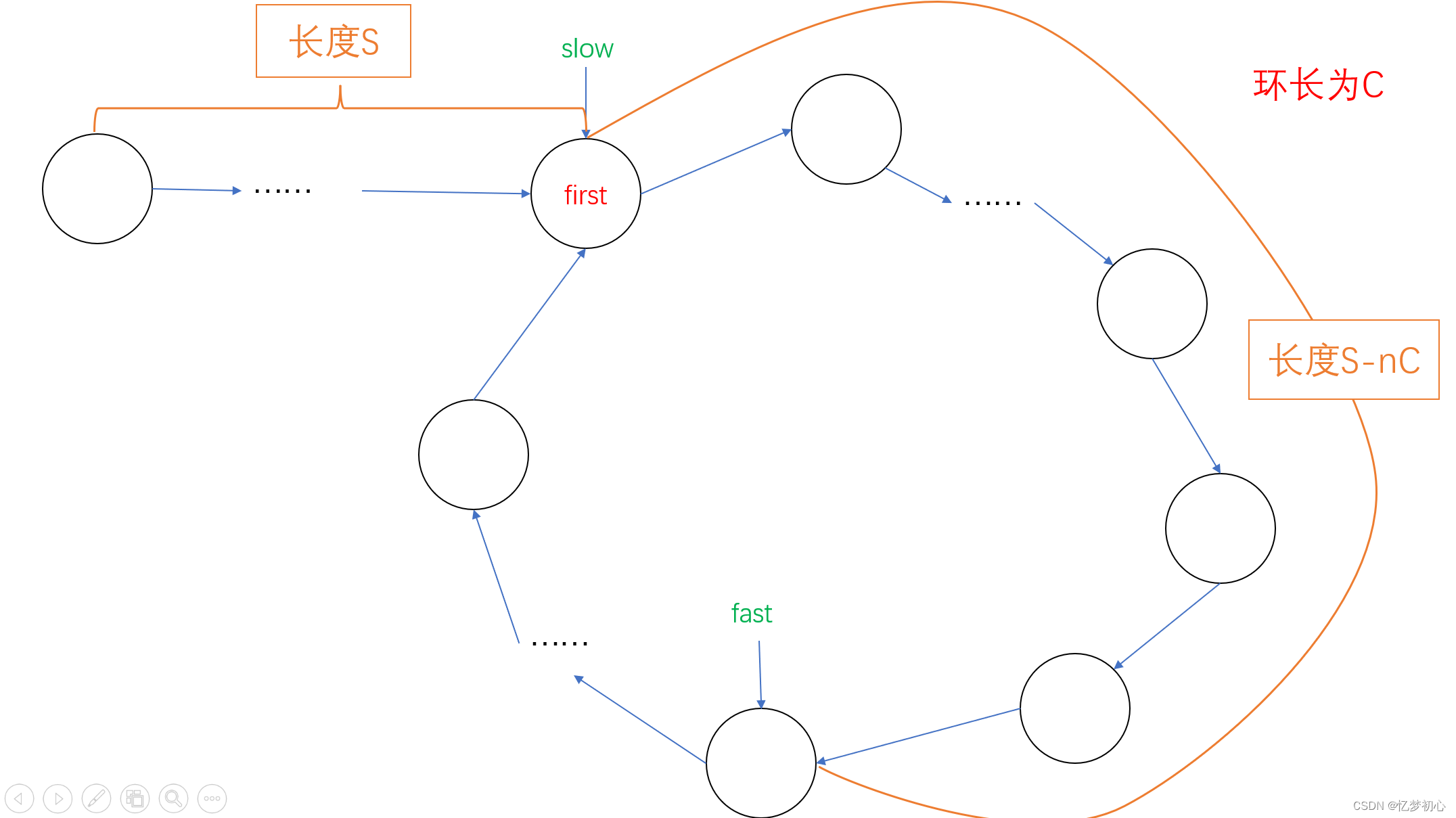
我们假设此时快慢指针的距离为L,这里可能有读者有疑问:快指针是慢指针速度的2倍,那L的大小不应该是S吗?实际上,当slow到达环入口时,fast可能已经绕环n圈了,所以fast实际走过的长度共为S+nC+L(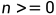 )。由此我们可以得出S+nC+L=2S,即L=S-nC。在这之后,快指针开始追逐慢指针,我们假设在如下位置相遇:
)。由此我们可以得出S+nC+L=2S,即L=S-nC。在这之后,快指针开始追逐慢指针,我们假设在如下位置相遇:

假设共进行了D次追逐才追上了慢指针,由快指针比慢指针快一倍可以得出以下关系:

因此,相遇点到快指针最初位置的距离为S-nC-D,由此可以得出相遇点到环结点的距离为S-nC-D+D=S-nC,如下:
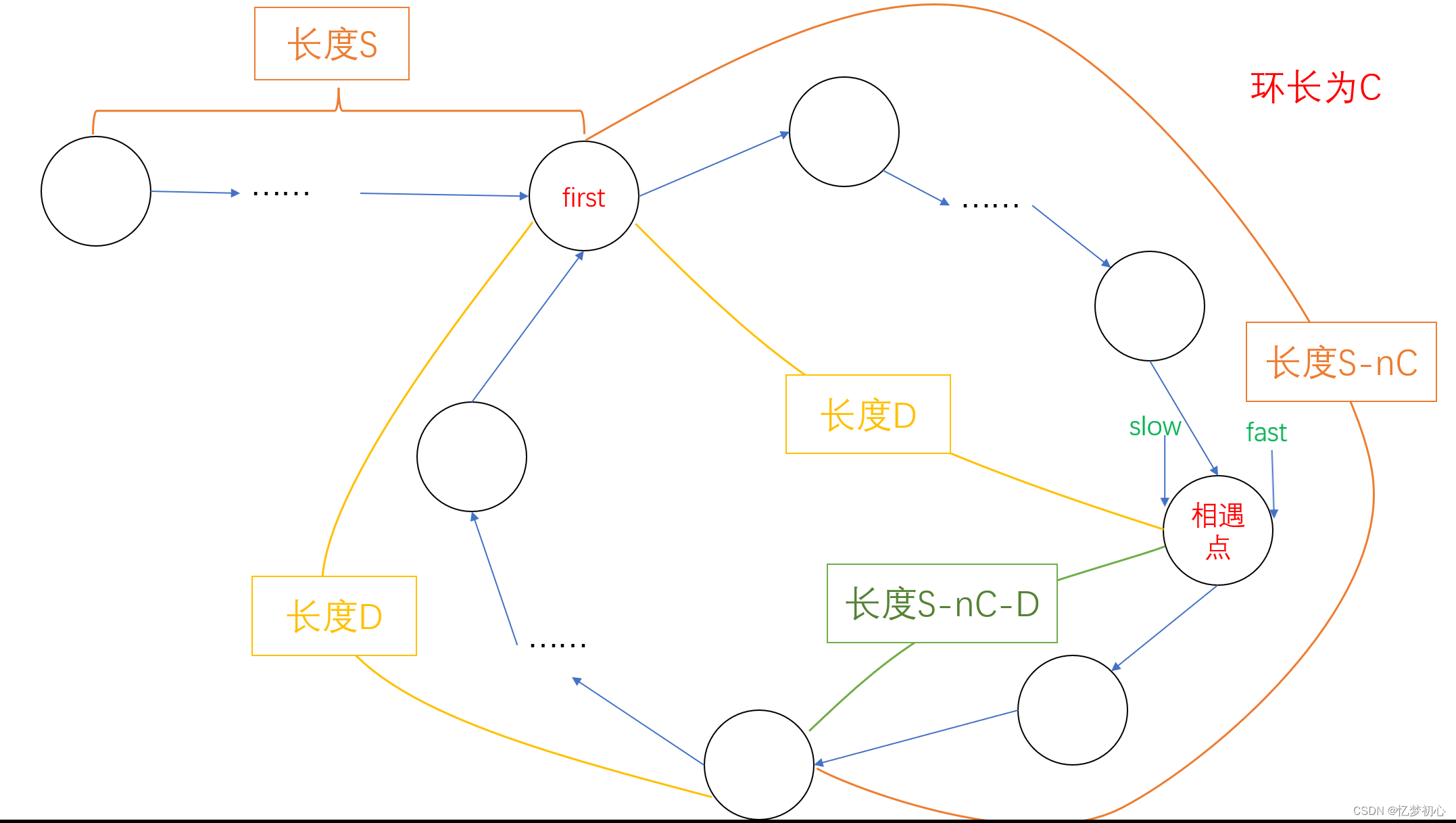
至此,我们发现链表头到环入口的距离S与相遇点到环入口的距离S-nC相差n个环的长度。
由此我们算法的思路是:
起初快指针速度为2,慢指针速度为1,如果快慢指针没有相遇,则返回NULL代表不存在环;如果相遇了,我们就让其中一个指针重新指向链表头,并使两个指针的速度都为1,一直前进直到它们相遇,相遇的位置一定为环的位置。这是因为从相遇点走S步后的位置与走S-nC步后的位置一致。
c.AC代码
struct ListNode {int val;struct ListNode* next;
};
struct ListNode* detectCycle(struct ListNode* head)
{struct ListNode* fast = head;struct ListNode* slow = head;while (fast && fast->next) //当到达或即将到达链表尾时退出循环{//快慢指针移动fast = fast->next->next;slow = slow->next;if (fast == slow) //相遇,存在环{//两个指针找环入口slow = head;while (slow!=fast){slow = slow->next;fast = fast->next;}return slow;}}return NULL;//没有相遇、没有结点、只有一个结点且非循环,不存在环,返回空} 求环形链表的环长💫
a.题目
给定一个链表的头节点 head ,返回链表环中环的长度。 如果链表无环,则返回 0。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。
b.题解分析
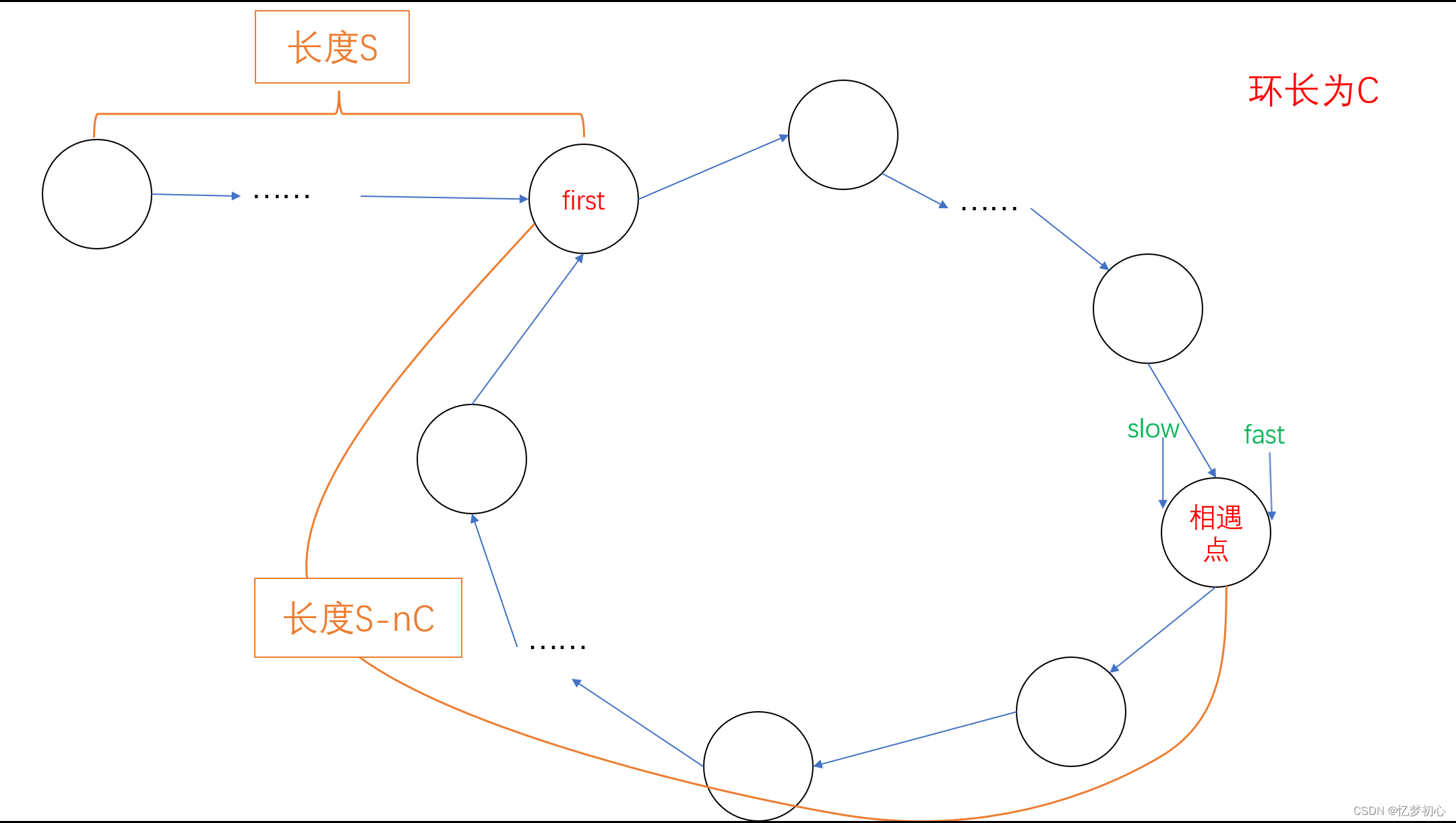
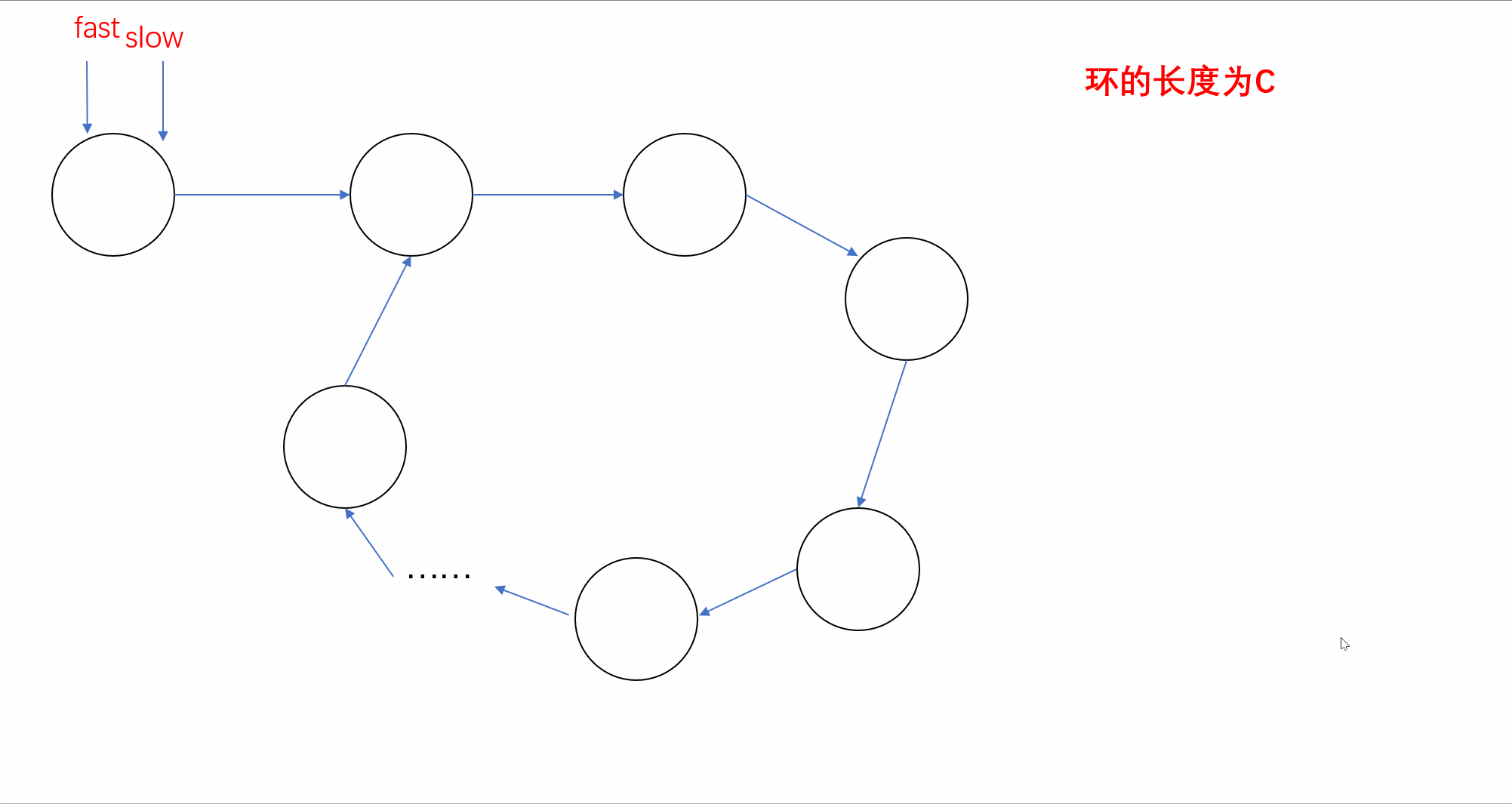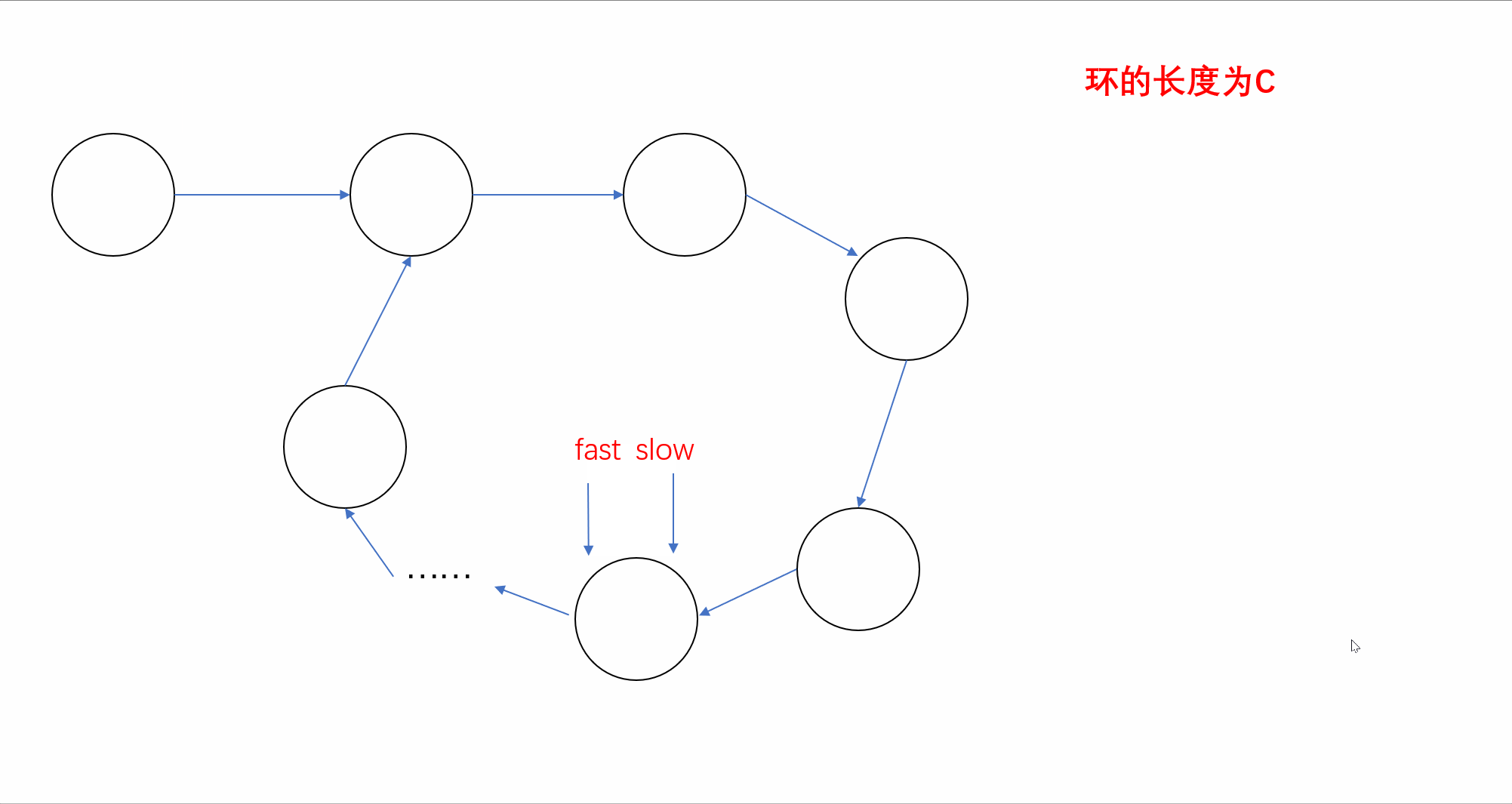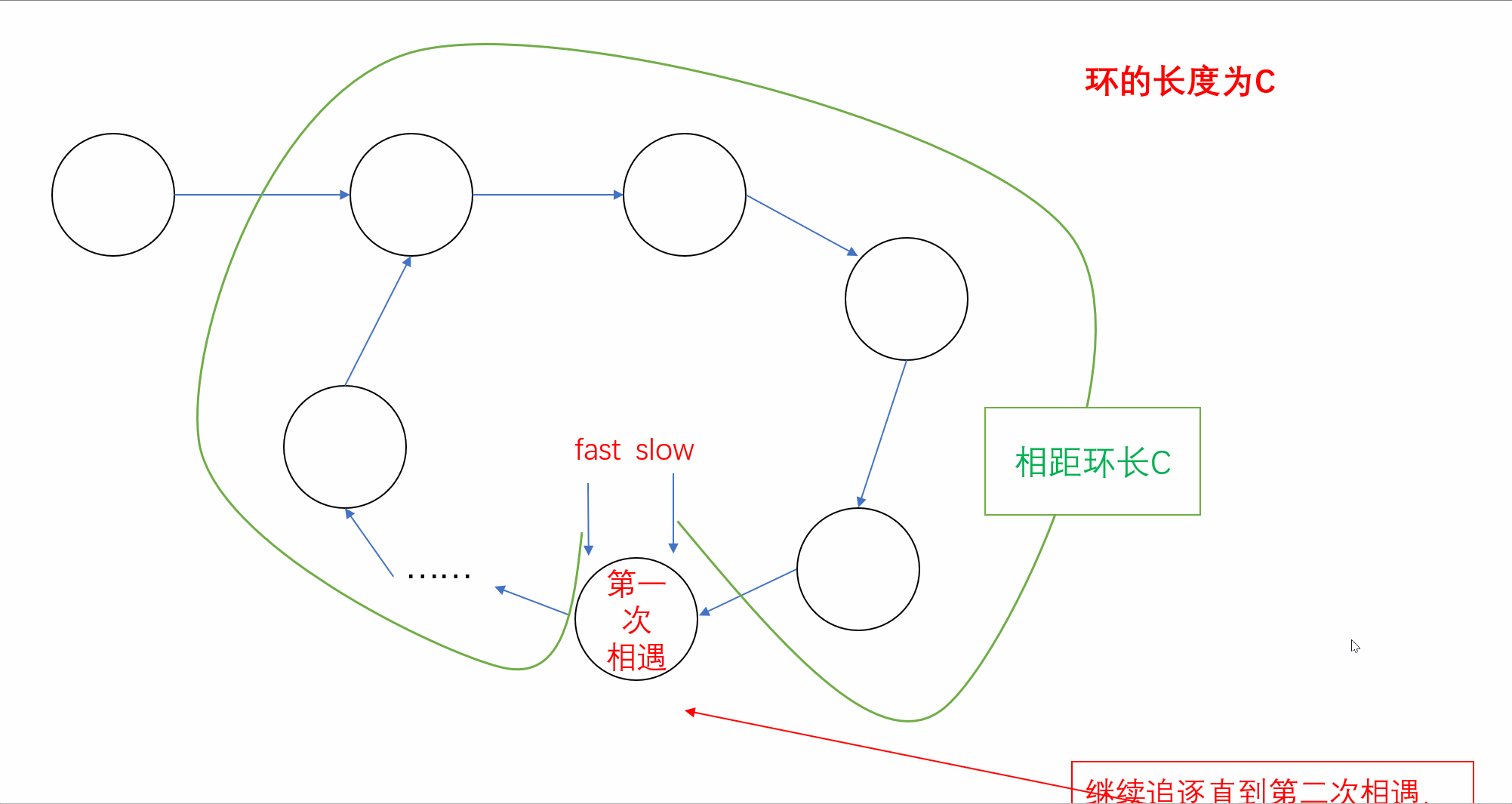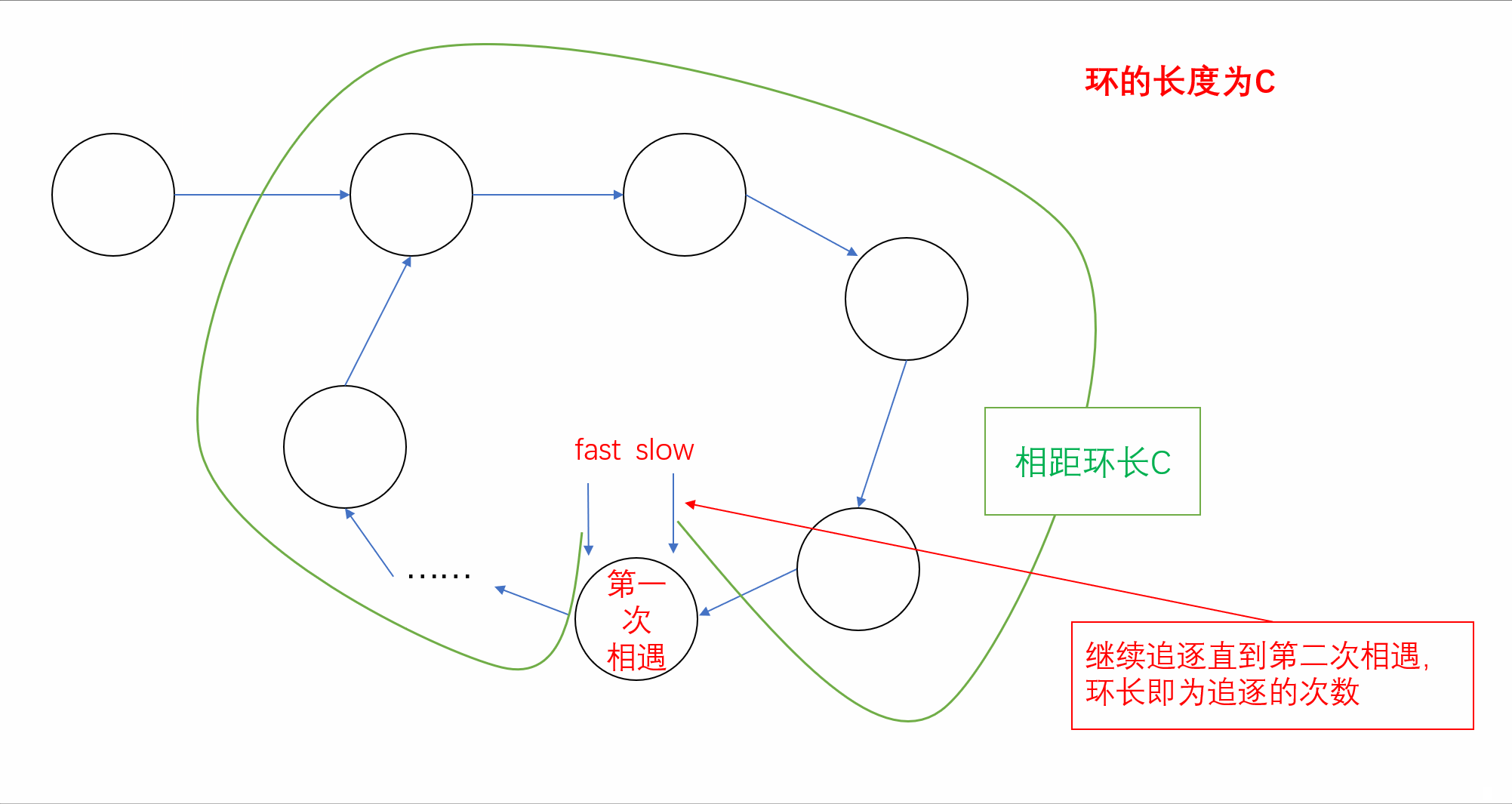
法一:我们同样可以先使用快慢指针判断链表是否存在环,当二者第一次相遇时说明链表存在环。而当快慢指针相遇后我们再次让快慢指针进行追逐战,此时它们之间的距离为环长C,由于每次追逐它们的距离都会缩短1,因此我们可以定义一个计数器count记录第二次相遇时所追逐的次数即为链表的环长。具体过程如下:
c.AC代码
struct ListNode {int val;struct ListNode* next;};
int CycleLength(struct ListNode* head)
{struct ListNode* fast = head;struct ListNode* slow = head;while (fast && fast->next) //当到达或即将到达链表尾时退出循环{//快慢指针移动fast = fast->next->next;slow = slow->next;if (fast == slow) //第一次相遇,存在环{//统计第二次相遇所追逐的次数int count = 0;do{fast = fast->next->next;slow = slow->next;count++;} while (fast != slow);//相遇了,返回追逐次数即为环长return count;}}//不存在环,返回0return 0;}以上,就是本期的全部内容啦🌸
制作不易,能否点个赞再走呢🙏
相关文章:

【刷题篇】链表(下)
前言🌸各位读者们好,本期我们来填填之前留下的坑,继续来讲解几道和链表相关的OJ题。但和上期单向链表不一样的是,我们今天的题目主要是于环形链表有关,下面让我们一起看看吧。💻本期的题目有:环…...
Shiro
Shiro 1.权限管理概述 2.Shiro权限框架 2.1 概念 2.2 Apache Shiro 与Spring Security区别 3.Shiro认证 3.1 基于ini认证 3.2 自定义Realm --认证 4.Shiro授权 4.1 基于ini授权 4.2 自定义realm – 授权 5.项目集成shiro 认证-授权注意点 5.1 认证…...
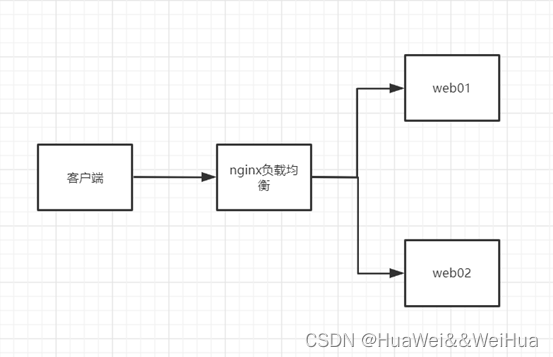
使用nginx进行负载均衡配置详细说明
使用nginx进行负载均衡 1. nginx负载均衡介绍 nginx应用场景之一就是负载均衡。在访问量较多的时候,可以通过负载均衡,将多个请求分摊到多台服务器上,相当于把一台服务器需要承担的负载量交给多台服务器处理,进而提高系统的吞吐…...

N皇后问题
#include<iostream> #include<string> #include<vector> using namespace std; #define MAX 20//最大20个皇后 int n ;//实际皇后个数 int sum ;//答案个数 vector<vector<int>> attack(MAX, vector<int>(MAX, 0));//标记攻击位置 vector&…...

强化学习DQN之俄罗斯方块
强化学习DQN之俄罗斯方块强化学习DQN之俄罗斯方块算法流程文件目录结构模型结构游戏环境训练代码测试代码结果展示强化学习DQN之俄罗斯方块 算法流程 本项目目的是训练一个基于深度强化学习的俄罗斯方块。具体来说,这个代码通过以下步骤实现训练: 首先…...

1.3总线:并行总线、串行总线、单工、半双工、全双工、总线宽度、总线带宽、总线的分类、数据总线、地址总线、控制总线
1.3总线:并行总线、串行总线、单工、半双工、全双工、总线宽度、总线带宽、总线的分类、数据总线、地址总线、控制总线总线并行总线、串行总线单工、半双工、全双工总线宽度总线带宽总线的分类数据总线(Data Bus,DB)地址总线&…...

Linux驱动开发—设备树开发详解
设备树开发详解 设备树概念 Device Tree是一种描述硬件的数据结构,以便于操作系统的内核可以管理和使用这些硬件,包括CPU或CPU,内存,总线和其他一些外设。 Linux内核从3.x版本之后开始支持使用设备树,可以实现驱动代…...

深入浅出C++ ——继承
文章目录一、继承的相关概念1. 继承的概念2. 继承格式3. 继承方式4. 访问限定符5. 继承基类成员访问方式的变化二、基类和派生类对象赋值转换三、继承中的作用域四、派生类的默认成员函数五、继承与友元六、继承与静态成员七、菱形继承及菱形虚拟继承1. 单继承2. 多继承3. 菱形…...
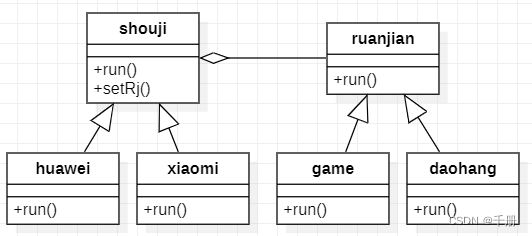
设计模式C++实现20: 桥接模式(Bridge)
部分内容参考大话设计模式第22章;本实验通过C语言实现。 一 基本原理 意图:将抽象部分和实现部分分离,使它们都可以独立变化。 上下文:某些类型由于自身的逻辑,具有两个或多个维度的变化。如何应对“多维度的变化”…...

Android中的Rxjava
要使用Rxjava首先要导入两个包,其中rxandroid是rxjava在android中的扩展 implementation io.reactivex:rxandroid:1.2.1implementation io.reactivex:rxjava:1.2.0observer 是一个观察者接口,泛型T为观察者观察数据的类型,里面只有三个方法&a…...

【RocketMQ】源码详解:消息储存服务加载、文件恢复、异常恢复
消息储存服务加载 入口:org.apache.rocketmq.store.DefaultMessageStore#load 在创建brokerContriller时会调用初始化方法初始化brokerController,在初始化方法中会进行消息储存服务的加载 this.messageStore.load(); 加载方法主要是加载一些必要的参数和数据,如配…...

数字IC设计工程师是做什么的?
随着我国半导体产业的发展,近几年的新入行的从业人员,除了微电子相关专业的,还有就是物理、机械、数学、计算机等专业,很多人对这一高薪行业充满了好奇,那么数字IC设计工程师到底是做什么的? 首先来看看数…...

【040】134. 加油站[简单模拟 + 逻辑转化]
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。 给定两个整数数组 gas 和 cost &am…...
Python用selenium实现自动登录和下单的脚本
前言 学python对selenium应该不陌生吧 Selenium 是最广泛使用的开源 Web UI(用户界面)自动化测试套件之一。Selenium 支持的语言包括C#,Java,Perl,PHP,Python 和 Ruby。目前,Selenium Web 驱动…...
Cartographer源码无死角解析-(55) 2D后端优化→AppendNode()、class MapById、 PoseGraphData、)
(02)Cartographer源码无死角解析-(55) 2D后端优化→AppendNode()、class MapById、 PoseGraphData、
讲解关于slam一系列文章汇总链接:史上最全slam从零开始,针对于本栏目讲解(02)Cartographer源码无死角解析-链接如下: (02)Cartographer源码无死角解析- (00)目录_最新无死角讲解:https://blog.csdn.net/weixin_43013761/article/details/127350885 文末正下方中心提供了本…...

如何在jmeter中把响应中的数据提取出来并引用
jmeter做接口测试过程中,经常遇到请求需要用到token的时候,我们可以把返回token的接口用后置处理器提取出来,但是在这种情况下,只能适用于当前的线程组,其他线程组无法引用到提取的token变量值,所以必须要生…...

2023环翠区编程挑战赛中学组题解
T1. 出栈序列 题目描述 栈是一种“先进后出”的数据结构,对于一个序列1,2,...,n1,2, ...,n1,2,...,n,其入栈顺序是1,2,...n1,2, ...n1,2,...n,但每个元素出栈的时机可以自由选择。 例如111入栈、111出栈,222入栈、333入栈、333…...

手撸一个Switch开关组件
一、前言 手撸系列又来了,这次咱们来撸一个Switch开关组件,废话不多说,咱们立刻发车。 二、使用效果 三、实现分析 首先我们先不想它的这个交互效果,我们就实现“不合格”时的一个静态页面,静态页面大致如下&#x…...
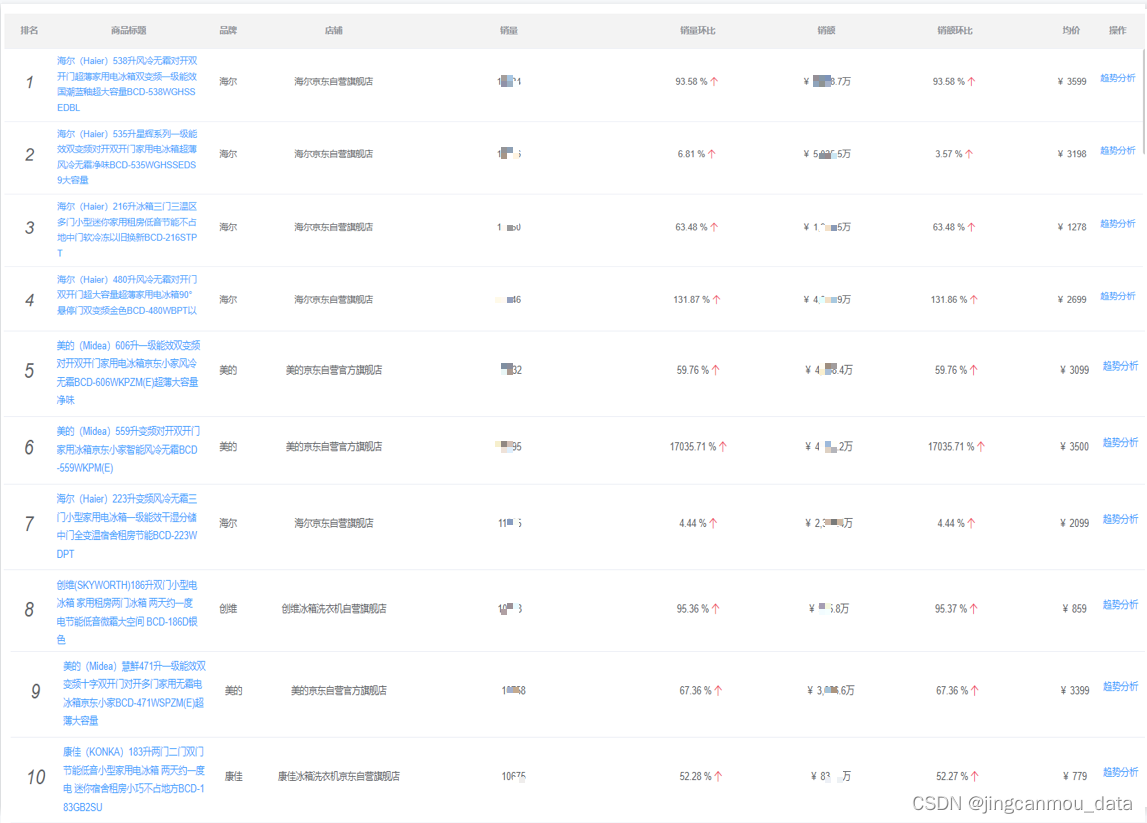
2023年1月冰箱品牌销量排行:销量环比增长26%,销售额36亿+
鲸参谋电商大数据2023年1月京东平台“冰箱”销售数据出炉! 根据鲸参谋平台电商数据显示,2023年1月份,在京东平台上,冰箱的销量将近130万件,环比增长26%,同比下滑8%;销售额达36亿,环比…...
DSP CCS 开发问题总结及解决办法
文章目录 问题汇总 1. CCS编译器的Project菜单栏工程导入选项丢失,怎么解决! 1.1启动CCS后发现导入工程菜单栏丢失,无法导入工程文件。 1.2方法一 工程选项的导入工程文件丢失,如果要重新获得相应的选项,就需要删除当前…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
