数学建模:回归分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
数学建模:回归分析
文章目录
- 数学建模:回归分析
- 回归分析
- 多元线性回归
- 案例
- 多项式回归
- 一元多项式回归
- 多元二项式回归
- 非线性回归
- 逐步回归
回归分析

多元线性回归
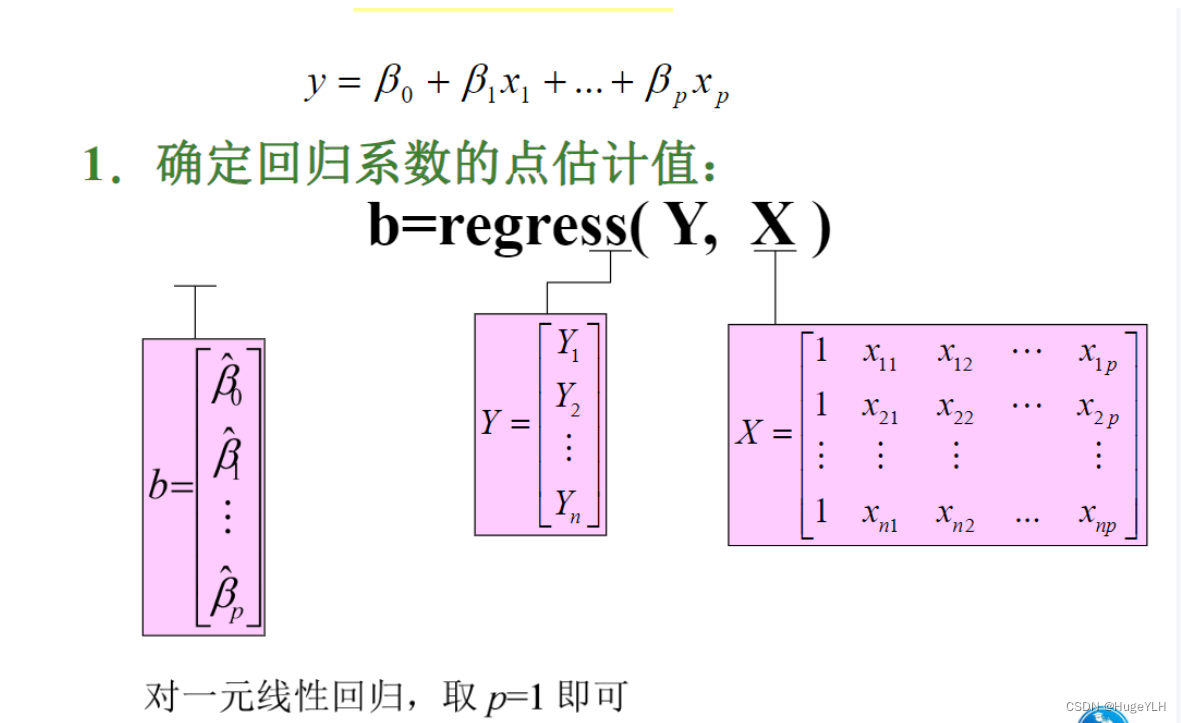
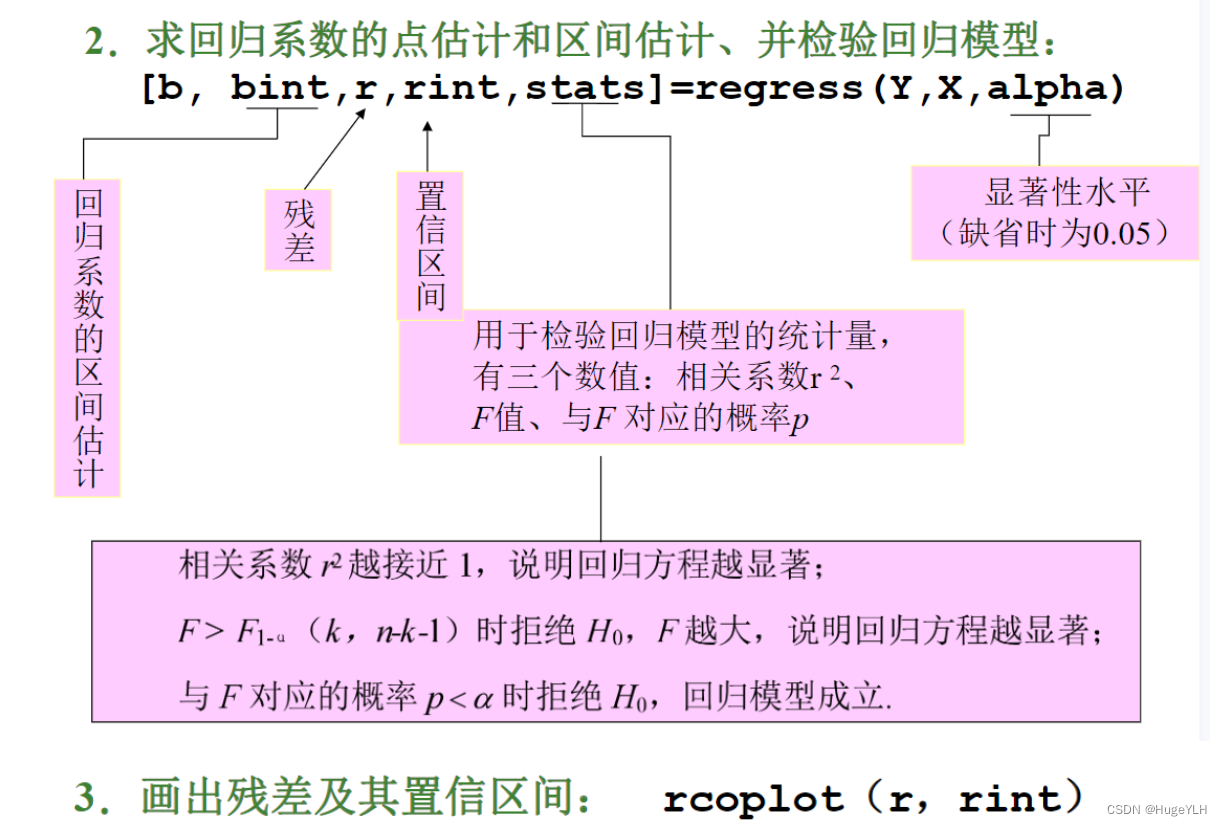
案例
- 首先进行回归分析
clc;clear;
x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';
X=[ones(16,1) x];
Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';%% 回归分析
[b,bint,r,rint,states] = regress(Y,X);
- p < 0.05 p<0.05 p<0.05 回归模型成立
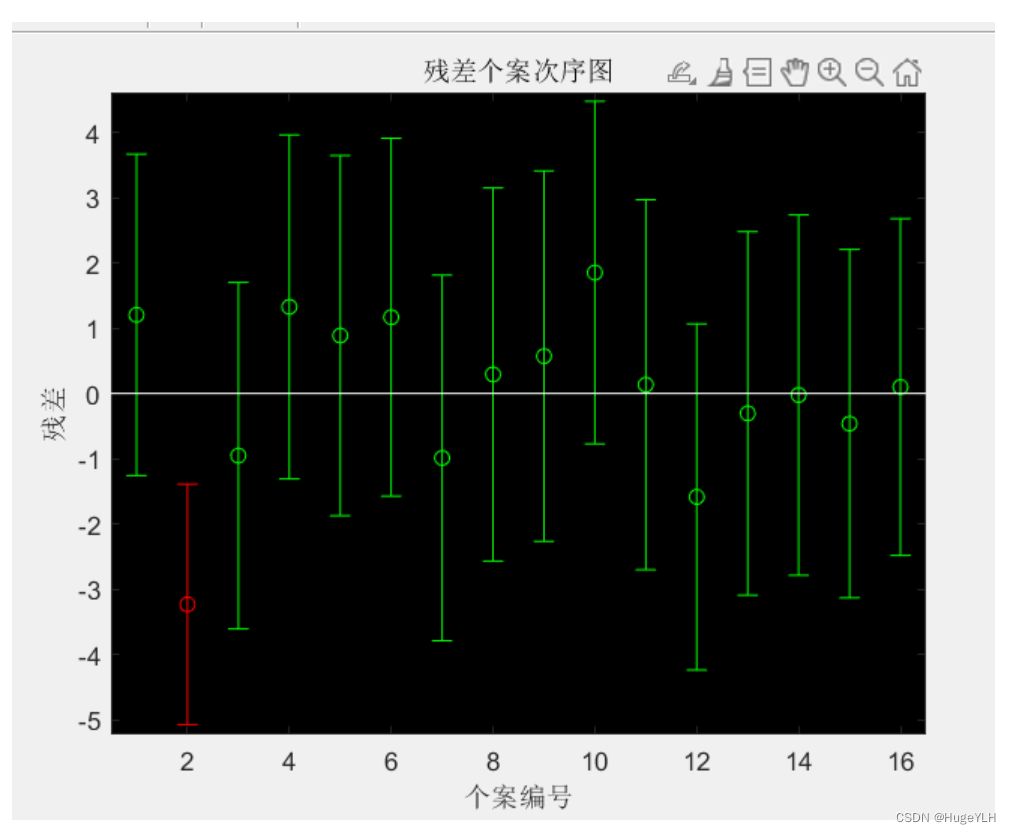
- 建立残差图
rcoplot(r,rint);
多项式回归
一元多项式回归

案例
- 直接做二次多项式回归
%% 一元多项式回归
clc;clear;x=1/30:1/30:14/30;
y=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
m=2;
%% 回归分析
[p,S] = polyfit(x,y,m);
% p(1)*x^2 + p(2)*x^1 + p(3)%% 绘图
polytool(x,y,m);%% 预测在某位置的值
polyval(p,0.1);%% 预测某位置的值并且返回置信区间
[Y,Delta] = polyconf(p,x,S,0.5);
- 化为多元线性回归
x=1/30:1/30:14/30;
y=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
T=[ones(14,1) x' (x.^2)'];
[b,bint,r,rint,stats]=regress(y',T);
b,stats
多元二项式回归

案例
- 直接多元二项式回归
x1=[1000 600 1200 500 300 400 1300 1100 1300 300];
x2=[5 7 6 6 8 7 5 4 3 9];
y=[100 75 80 70 50 65 90 100 110 60]';
x=[x1' x2'];
rstool(x,y,'purequadratic')
- 化为多元线性回归
非线性回归



clc;clear;x = 2:16;
y = [2,3,4,5,7,4,3,6,8,9,4,1,0,5,4];
beta0 = [8 2]';
%% 非线性回归分析
[beta,r,J] = nlinfit(x',y','Volum',beta0);%% 预测与绘图
[YY,delta] = nlpredci('Volum',x',beta,r,J);
plot(x,y,'k+',x,YY,'r');------
%% 拟合模型: y = a*e^(b/x)
function y = Volum(beta,x)y = beta(1)*exp(beta(2)./x);
end
逐步回归

25 回归分析算法基本原理及编程实现.pdf
相关文章:

数学建模:回归分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:回归分析 文章目录 数学建模:回归分析回归分析多元线性回归案例 多项式回归一元多项式回归多元二项式回归 非线性回归逐步回归 回归分析 多元线性回归 案例 首先进行回归分…...
)
数据库(一)
数据库 1.为什么要使用数据库 如果要存储数据,我们是可以使用文件来存储数据的,但是使用文件管理数据有很多缺点,比如: 不安全,不利于管理,查询,如果要存储大量的数据,使用文件管理…...
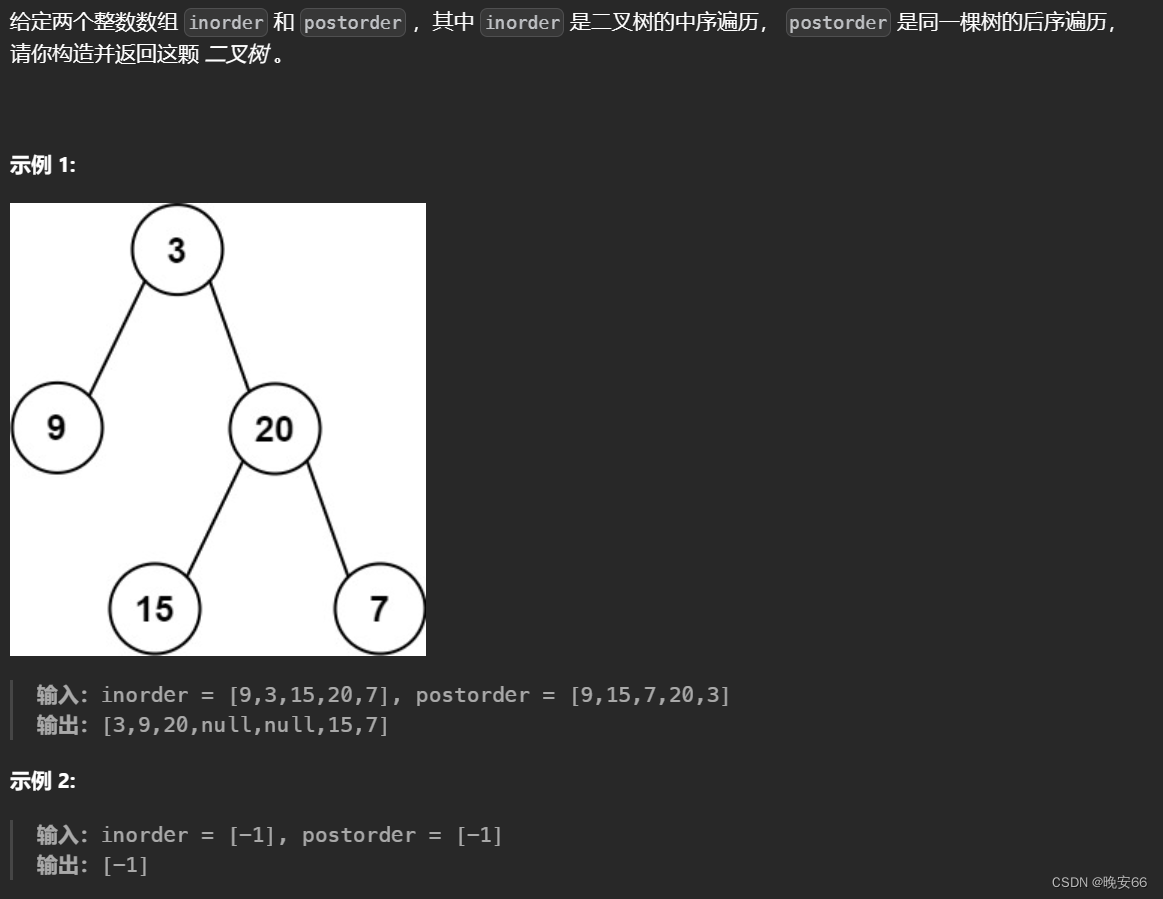
【算法与数据结构】106、LeetCode从中序与后序遍历序列构造二叉树
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:首先我们要知道后序遍历数组的最后一个元素必然是根节点,然后根据根节点在中序遍历数组中的…...
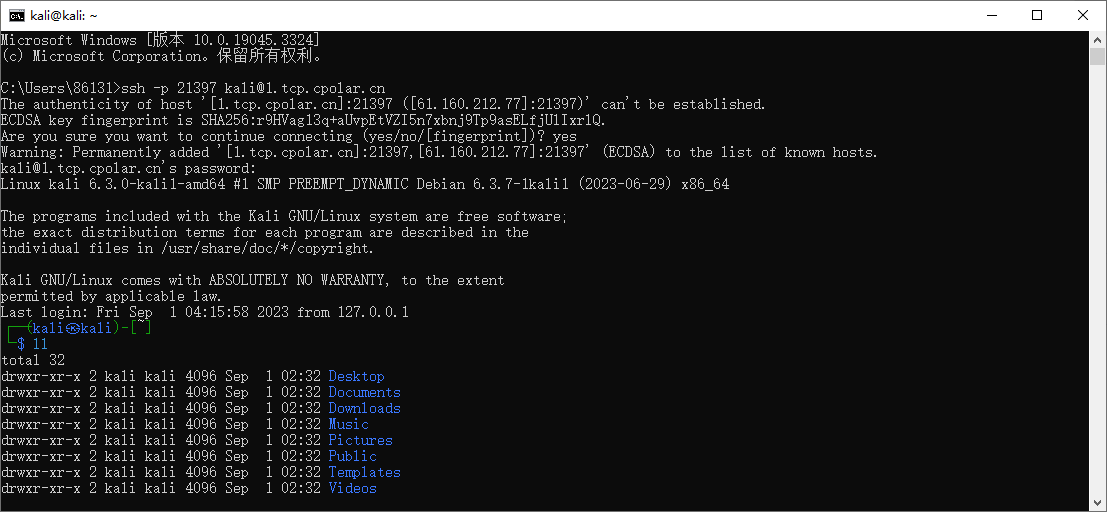
kali 安装cpolar内网穿透实现 ssh 远程连接
文章目录 1. 启动kali ssh 服务2. kali 安装cpolar 内网穿透3. 配置kali ssh公网地址4. 远程连接5. 固定连接SSH公网地址6. SSH固定地址连接测试 简单几步通过cpolar 内网穿透软件实现ssh 远程连接kali! 1. 启动kali ssh 服务 默认新安装的kali系统会关闭ssh 连接服务,我们通…...

算法训练 第一周
一、合并两个有序数组 本题给出了两个整数数组nums1和nums2,这两个数组均是非递减排列,要求我们将这两个数组合并成一个非递减排列的数组。题目中还要求我们把合并完的数组存储在nums1中,并且为了存储两个数组中全部的数据,nums1中…...

软件评测师之码制
目录 一、机器数二、码制三、数的表示范围 一、机器数 机器数就是一个数在计算机中的二进制表示,计算机中机器数的最高位是符号位,正数符号位为0,负数符号位为1,机器数包含原码、反码和补码三种表示形式。 二、码制 表现形式数…...

ubuntu18安装cmake27的方法
背景是ubuntu18默认的cmake是3.10 $ apt search cmake Sorting... Done Full Text Search... Done bear/bionic,bionic 2.3.11-1 allgenerate compilation database for Clang toolingcatkin/bionic,bionic 0.7.8-1 allLow-level build system macros and infrastructure for …...
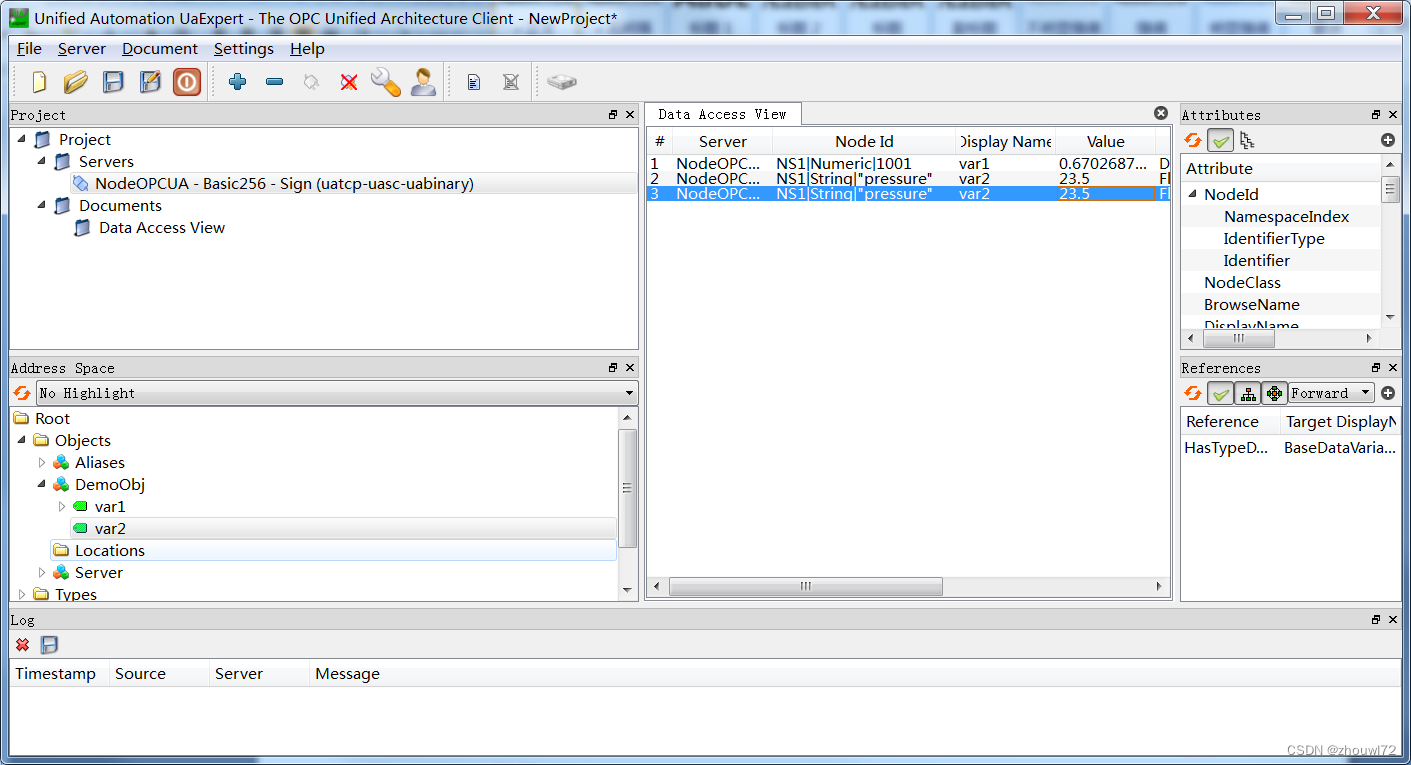
通讯编程006——NodeJS OPC UA Client开发简单教程
本文介绍如何在NodeJS环境下开发OPC UA Client,通过本文可以对OPC UA的基本概念有所了解,掌握OPC UA的本质。相关软件请登录网信智汇(wangxinzhihui.com)。 开发步骤如下: 1)首先需要安装nodejs,要求版本至少是12。 …...

「高等数学」雅可比矩阵和黑塞矩阵的异同
「高等数学」雅可比矩阵和黑塞矩阵的异同 雅可比矩阵,Jacobi matrix 或者 Jacobian,是向量值函数( f : R n → R m f:\mathbb{R}^n \to \mathbb{R}^m f:Rn→Rm)的一阶偏导数按行排列所得的矩阵。 黑塞矩阵,又叫海森矩…...
继承(个人学习笔记黑马学习)
1、基本语法 #include <iostream> using namespace std; #include <string>//普通实现页面//Java页面 //class Java { //public: // void header() { // cout << "首页、公开课、登录、注册...(公共头部)" << endl; // } // void footer() …...

ToBeWritten之ATTCK 测评方案
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 转移发布平台通知:将不再在CSDN博客发布新文章,敬…...

JSONUtil详解
JSONUtil是一个通用的JSON工具类,用于在Java中操作JSON数据。虽然之前提到的示例中没有直接提及JSONUtil,但可以解释一下可能存在的一些常见JSON操作方法,这些方法通常可以在不同的JSON工具类中找到。 JSONUtil中的一些常见方法包括…...
ArcGIS Maps SDK for JS(一):概述与使用
文章目录 1 概述2 如何使用ArcGIS Maps SDK for JavaScript2.1 AMD 模块与 ES 模块2.2 AMD 模块和 ES 模块比较 3 几种安装方式3.1 通过 ArcGIS CDN 获取 AMD 模块3.2 通过 NPM 运行 ES 模块3.3 通过 CDN 获取 ES 模块3.4 本地构建 ES3.5 本地构建 AMD 3 VSCode下载与安装2.1 下…...

【STM32】FSMC接口的复用和非复用
问题背景 在阅读《零死角玩转STM32—F103指南者》,以及《STM32F10x-中文参考手册》关于FSMC一章节的时候,对于在控制NOR/SRAM的时候使用到的引脚,在提到NOR器件的时候提到了地址复用和非复用接口,一时间没明白是什么东西。 结论 非复用模式…...

操作系统强化认识之Shell编程学习与总结
目录 1.Shell的概述 2.Shell脚本入门 3.变量 3.1.系统预定义变量 3.2.自定义变量 3.3.特殊变量 4.运算符 5.条件判断 6.流程控制 6.1.if判断 6.2.case语句 6.3.for循环 6.4.while循环 7.read读取控制台输入 8.函数 8.1.系统函数 8.2.自定义函数 9.正则表示式入…...
怎么用conda下载清华源的pytorch(自带cuda的版本)
1,添加镜像源 conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

【ES6】CommonJS模块和ES6模块
在JavaScript中,模块是一种将功能代码组织成逻辑单元的方式,以便在其他项目中重复使用。有两种主要的模块系统:CommonJS和ES6。 1、CommonJS 在CommonJS中,我们使用require来引入模块,使用module.exports来导出模块。…...
两个线程同步执行:解决乱箭穿心(STL/Windows/Linux)
C自学精简教程 目录(必读) C并发编程入门 目录 多线程同步 线程之间同步是指线程等待其他线程执行完某个动作之后再执行(本文情况)。 线程同步还可以是像十字路口的红绿灯一样,只允许一个方向的车同行,其他方向的车等待。 本…...
)
Ubuntu18.04更改镜像源(网易,阿里,清华,中科大,浙大)
一,备份原来的源(选做) sudo cp /etc/apt/sources.list /etc/apt/sources_init.list 二,更换源 sudo gedit /etc/apt/sources.list 删除原来内容改为新的镜像源 1,清华源 deb https://mirrors.tuna.tsinghua.edu…...

字节码和机器码的区别
字节码和机器码是计算机程序在不同阶段的表示形式,它们的主要区别如下: 抽象级别不同:字节码是一种中间表示形式,位于源代码和机器码之间。它是一种与特定平台无关的低级表示形式,通常由编译器将源代码转换而来。而机器…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
