linux centos7 系统之编程:求水仙花数
在Python编程中,有列表、元组和字典三类变量可以使用,方便数据的存储与处理,而bash中仅有字符串变量、数组、函数可用,方法运用上受到限制,这与bash基于C语言,注重语法结构的严谨有关。而Python等高级语言更侧重于数据的组合与复用,方便处理,也与现代内存增大,价格低廉有关。
本文在介绍python使用的同时,重点讨论用bash编程求水仙花数。
水仙花数指一个三位数:每位数的3次方之和等于这个数。
例如:153是一个水仙花数:153=1^3+5^3+3^3
我们本案例目标:打印输出所有的水仙花数,从小数开始,升序。每行一个。
一、python语言实现
用python语言实现输出水仙花数的功能,十分方便。
首先,设置一个循环变量,一个3位数的整数,从100取值开始,一一验证,每位数的3次方相加与此数相比较,相等为水仙花数(记录、打印),不相等时,变量取值自动加1,再进行验证,如此循环,直到999为止。如此就可以查找并打印出所有的水仙花数。
for循环:
for i in range(100,1000)
python循环取值:开始100,结束1000-1(1000不取值)
对于每一个数,要计算其每位数的3次方之和,有多种方法:
1.先转$i为字符型数据,再对每一位切片,求出其整数之3次方
2.由$i对10求余,求模,得到每一位数,求出其整数之3次方
定义一个变量sum记录每一个数的各位数之3次方之和
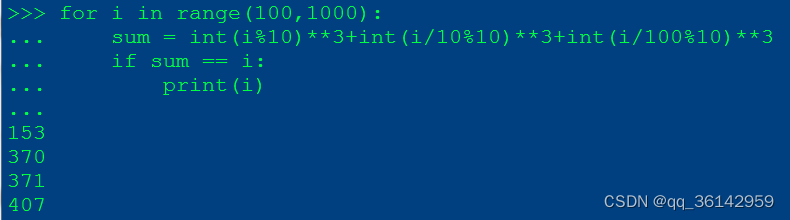
1.由求余数计算立方和
for i in range(100,1000):
sum = int(i%10)**3+int(i/10%10)**3+int(i/100%10)**3
if sum == i:
print(i)
2.由字符切片获得各位数
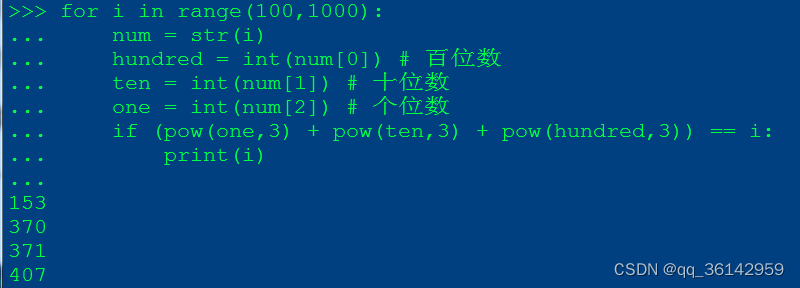
a.用pow()函数求3次方
由切片可以获得字符串的各个元素,再转为整型数值,用pow()函数求3次方
for i in range(100,1000):
num = str(i)
hundred = int(num[0]) # 百位数
ten = int(num[1]) # 十位数
one = int(num[2]) # 个位数
if (pow(one,3) + pow(ten,3) + pow(hundred,3)) == i:
print(i)
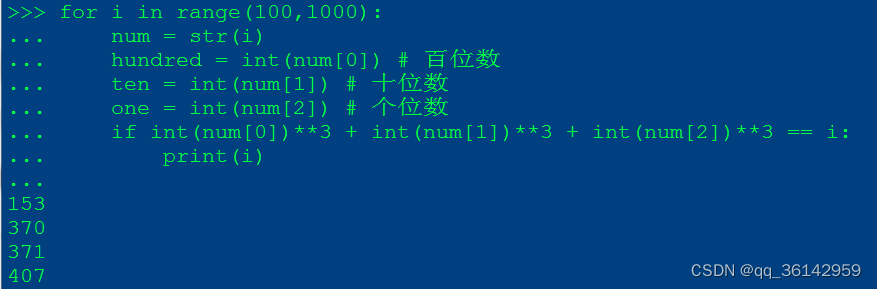
b.用m**n计算m的n次方
由切片可以获得字符串的各个元素,再转为整型数值,用m**n计算m的n次方
for i in range(100,1000):
num = str(i)
hundred = int(num[0]) # 百位数
ten = int(num[1]) # 十位数
one = int(num[2]) # 个位数
if int(num[0])**3 + int(num[1])**3 + int(num[2])**3 == i:
print(i)
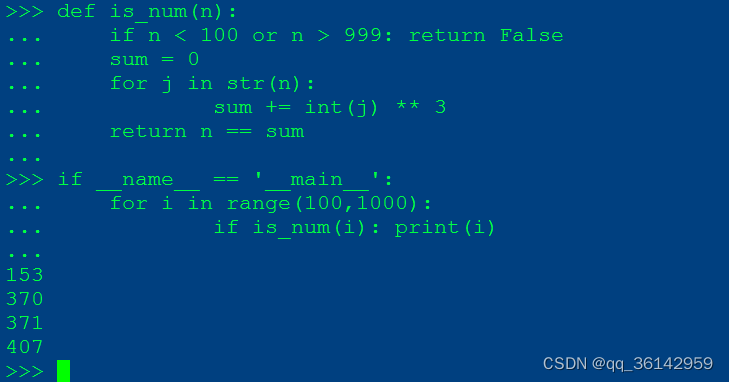
3.由函数达得目标
用定义函数来进行测试。
def is_num(n):
if n < 100 or n > 999: return False
sum = 0
for j in str(n):
sum += int(j) ** 3
return n == sum
if __name__ == '__main__':
for i in range(100,1000):
if is_num(i): print(i)
二、bash语言实现
Linux下用bash语言实现输出水仙花数的功能,方法和代码基本上与python相同。
除循环结构写法不太一样,对变量的处理也有稍微差别。思路与方法相同,就可以快速改写,完成目标。
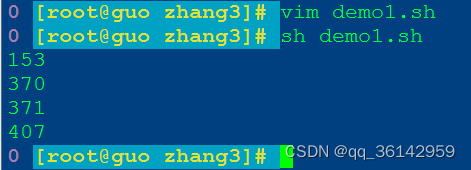
1.多层for循环嵌套
#!/bin/bash
# 求水仙花数
for((i=1;i<10;i++))
do
for((j=0;j<10;j++))
do
for((k=0;k<10;k++))
do
a=$((i**3+j**3+k**3))
b=$((i*100+j*10+k))
if [ $a -eq $b ];then
echo "$a"
fi
done
done
done

把一个三位数,取得每一位数字,这里用了最直观的想法:
取每一位数字,再计算3次方,相加就可以了。
更有效率的方法是:不断地除10取余。
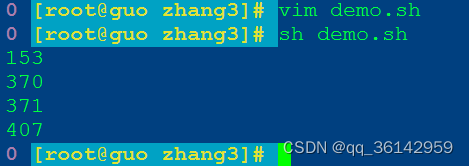
2.while循环求数字的各位数
#!/bin/bash
for ((i=100;i<=999;i++))
do
sum=0
n=$i
while [ $n -gt 0 ]
do
m=$((n%10)) # 通过对10求余数,第一次得到个位数
sum=$((sum+m*m*m)) # 每次求出位数的3次方,进行累加
n=$((n/10)) # 个位数处理完后,再把原数对10取整
# 据此,进行第二次循环,第三次循环
done
if [ $sum -eq $i ];then
echo $i
fi
done
题外话
bash代码求四季花数:
取一个四位数,如果它的每个位上的数字的4次方和与自身相等,则可以称之为四季花数。
与3位的水仙花数相同,计算每位数的4次方之和,再验证是否等于这个四位数。
我们修改一下水仙花数求解代码,在命令行执行。写成一行代码,方便快速执行。
for ((i=1000;i<=9999;i++)); do sum=0; n=$i; while [ $n -gt 0 ];do k=$((n%10)); sum=$((sum+k*k*k*k)); n=$((n/10)); done; if [ $sum -eq $i ]; then echo "四季花数是 $i"; fi; done

扩展设想
其实这类问题还可以扩展为更一般的问题:
有一个N位数,如果它的每一位数字的N次方之和等于自身,则称它为N阶的花朵数。
请求出所有的10阶花朵数。
这个问题就要考虑效率了!感兴趣的可以深入探讨。
相关文章:

linux centos7 系统之编程:求水仙花数
在Python编程中,有列表、元组和字典三类变量可以使用,方便数据的存储与处理,而bash中仅有字符串变量、数组、函数可用,方法运用上受到限制,这与bash基于C语言,注重语法结构的严谨有关。而Python等高级语言更…...

git中的cherry-pick和merge有些区别以及cherry-pick怎么用
git中的cherry-pick和merge在使用场景上有些区别: cherry-pick用于将另一个分支的某一次或几次commit应用到当前分支。它可以选择性地拉取代码修改。merge用于将两个分支合并成一个新分支。它会把整个分支上的所有修改都合并过来。 具体区别:cherry-pick通常用于将bug修复从发…...
【前端】CSS-Flex弹性盒模型布局
目录 一、前言二、Flex布局是什么1、任何一个容器都可以指定为Flex布局2、行内元素也可以使用Flex布局3、Webkit内核的浏览器,必须加上-webkit前缀 三、基本概念四、flex常用的两种属性1、容器属性2、项目属性 五、容器属性1、flex-direction①、定义②、语句1&…...

Android AAPT: error: resource color 异常原因处理
异常体现: Android resource linking failed ERROR:E:\software\Developer\APP\GaoDeTest2\app\src\main\res\values\themes.xml:3:5-9:13: AAPT: error: resource color/purple_500 (aka com.example.gaodetest2:color/purple_500) not found.ERROR:E:\software\De…...
的概念)
C++std::function和std::bind()的概念
std::function: 一个通用的函数封装器,它允许你存储和调用任何可以被调用的东西,例如函数、函数指针、函数对象、Lambda 表达式等。 std::bind: 用于创建函数对象。一个可调用对象的绑定版本,可以提前绑定某些参数&am…...

QT Creator工具介绍及使用
一、QT的基本概念 QT主要用于图形化界面的开发, QT是基于C编写的一套界面相关的类库,如进程线程库,网络编程的库,数据库操作的库,文件操作的库等。 如何使用这个类库:类库实例化对象(构造函数) --> 学习…...

python爬虫13:pymysql库
python爬虫13:pymysql库 前言 python实现网络爬虫非常简单,只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点,方便以后复习。 申明 本系列所涉及的代码仅用于个人研究与讨论,并不会对网站产生…...

权限管理 ACL、RBAC、ABAC的学习
ACL(Access Control List:访问控制列表) 最简单的一种方式,将权限直接与用户或用户组相关联,管理员直接给用户授予某些权限即可。 这种模型适用于小型和简单系统,权限一块较为简单,并且角色和权限的变化较少。 RBAC(R…...

python的re正则表达式
一、正在表达式的方法(): re是Python中用于处理正则表达式的内置库,提供了许多有用的方法。以下是其中几个常用的方法: re.match(pattern, string): 尝试从字符串的开头匹配一个模式,如果匹配成功则返回匹…...

【算法与数据结构】700、LeetCode二叉搜索树中的搜索
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:二叉搜索树的性质:左节点键值 < 中间节点键值 < 右节点键值。那么我们根据此性质&am…...
SpringBoot v2.7.x+ 整合Swagger3入坑记?
目录 一、依赖 二、集成Swagger Java Config 三、配置完毕 四、解决方案 彩蛋 想尝鲜,坑也多,一起入个坑~ 一、依赖 SpringBoot版本:2.7.14 Swagger版本:3.0.0 <dependency><groupId>com.github.xiaoymin<…...
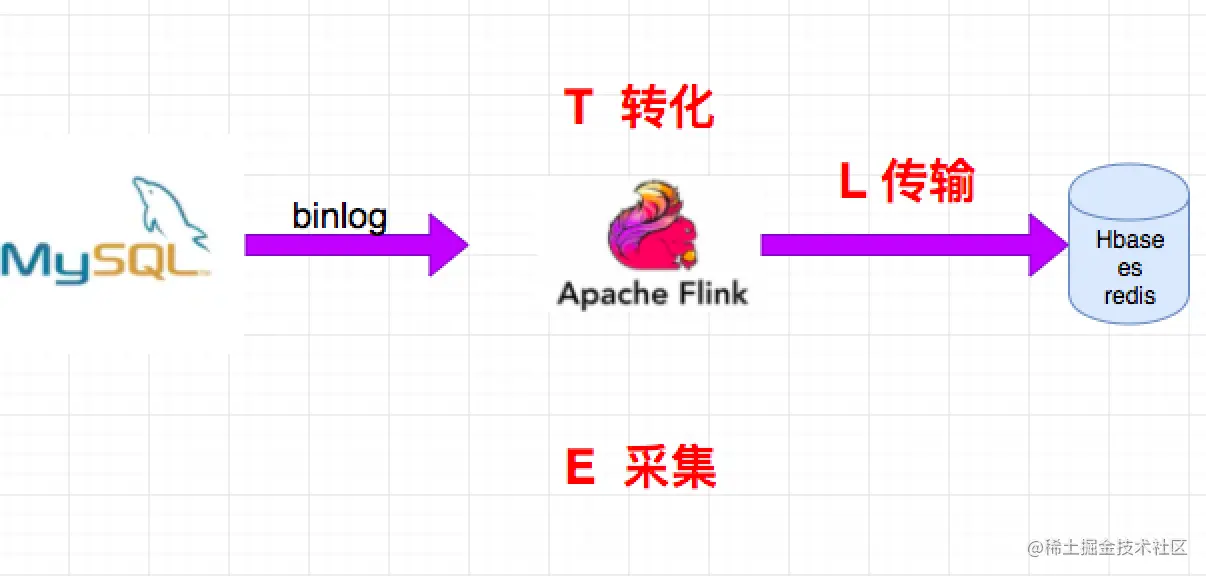
说说你了解的 CDC
分析&回答 什么是 CDC CDC,Change Data Capture,变更数据获取的简称,使用CDC我们可以从数据库中获取已提交的更改并将这些更改发送到下游,供下游使用。这些变更可以包括INSERT,DELETE,UPDATE等。用户可以在以下的场景下使用CDC: 使用f…...

SpingMvc入门
SpingMvc入门 1.MVC Spring的工作流程:2.sping mvc入门3.静态资源处理 前言 Spring MVC是一种基于Java的web应用开发框架,它采用了MVC(Model-View-Controller)设计模式来帮助开发者组织和管理应用程序的各个组件。 1.MVC Spring的…...
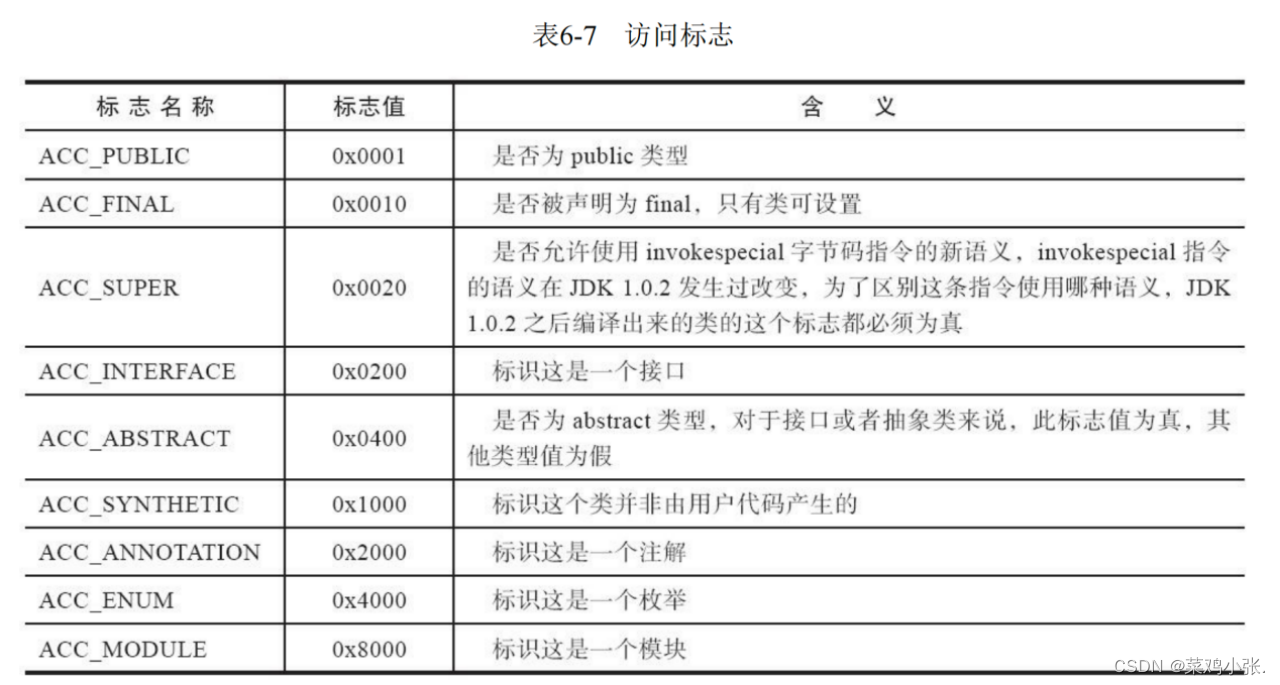
JVM的故事——类文件结构
类文件结构 文章目录 类文件结构一、概述二、无关性基石三、Class类文件的结构 一、概述 计算机是只认由0、1组成的二进制码的,不过随着发展,我们编写的程序可以被编译成与指令集无关、平台中立的一种格式。 二、无关性基石 对于不同平台和不同平台的…...

springboot自定义表格(动态合并单元格)
一、需求展示(一个订单多个商品,商品数量不限订单行合并) 二、技术选型(jxls自定义模板) <!-- 版本具体看官网Release,这里我们使用 2.13.0 --><dependency><groupId>org.jxls</group…...
)
C++零碎记录(二)
3. 调用其他类 3.1 类中有其他的类 #include <iostream> using namespace std;//点和圆关系案例//点类 class Point { public://设置xvoid setX(int x){m_X x;}//获取xint getX(){return m_X;}//设置yvoid setY(int y){m_Y y;}//获取yint getY(){return m_Y;}private…...

数学建模:回归分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:回归分析 文章目录 数学建模:回归分析回归分析多元线性回归案例 多项式回归一元多项式回归多元二项式回归 非线性回归逐步回归 回归分析 多元线性回归 案例 首先进行回归分…...
)
数据库(一)
数据库 1.为什么要使用数据库 如果要存储数据,我们是可以使用文件来存储数据的,但是使用文件管理数据有很多缺点,比如: 不安全,不利于管理,查询,如果要存储大量的数据,使用文件管理…...
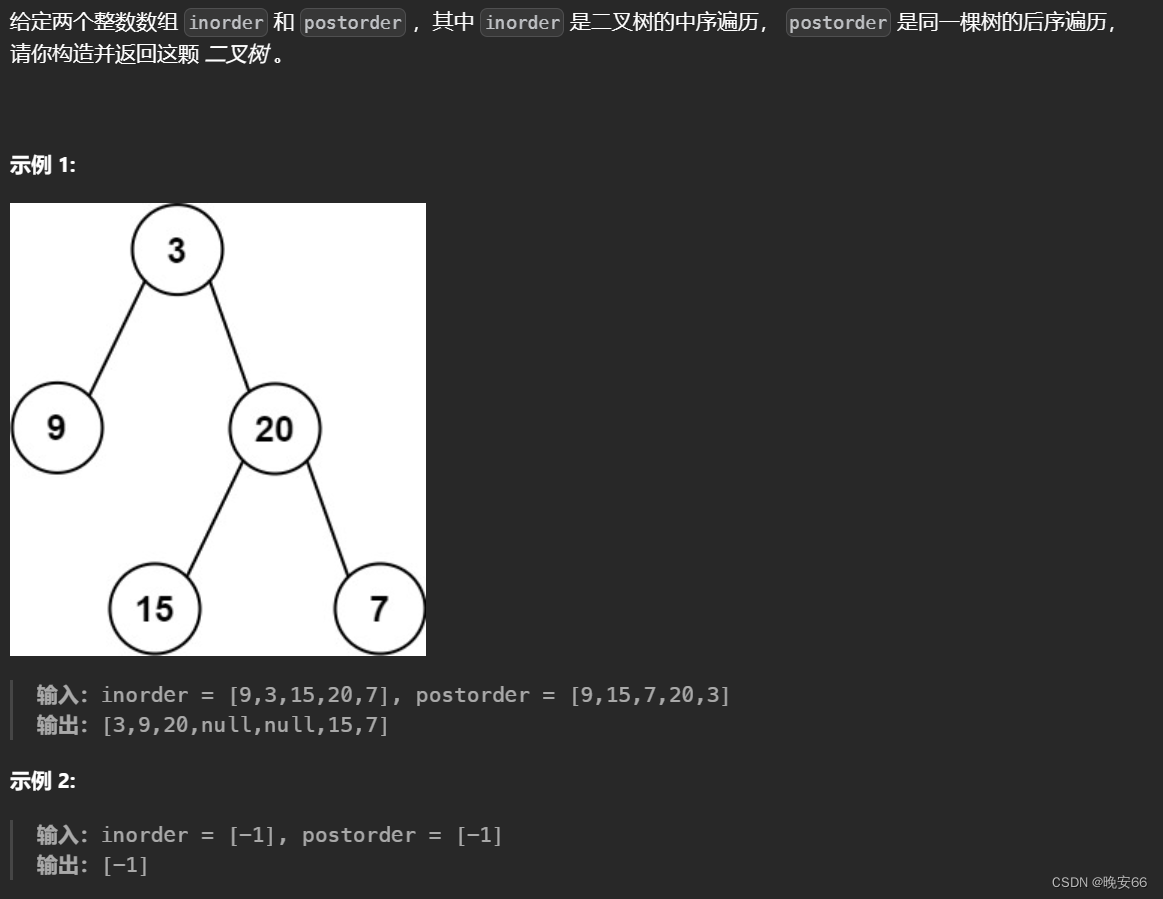
【算法与数据结构】106、LeetCode从中序与后序遍历序列构造二叉树
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:首先我们要知道后序遍历数组的最后一个元素必然是根节点,然后根据根节点在中序遍历数组中的…...
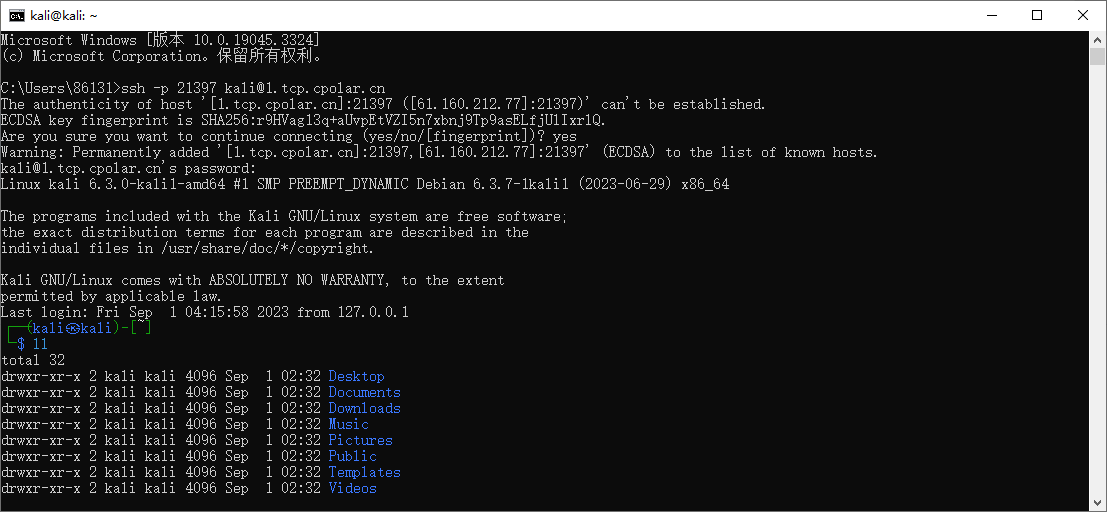
kali 安装cpolar内网穿透实现 ssh 远程连接
文章目录 1. 启动kali ssh 服务2. kali 安装cpolar 内网穿透3. 配置kali ssh公网地址4. 远程连接5. 固定连接SSH公网地址6. SSH固定地址连接测试 简单几步通过cpolar 内网穿透软件实现ssh 远程连接kali! 1. 启动kali ssh 服务 默认新安装的kali系统会关闭ssh 连接服务,我们通…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...

linux设备重启后时间与网络时间不同步怎么解决?
linux设备重启后时间与网络时间不同步怎么解决? 设备只要一重启,时间又错了/偏了,明明刚刚对时还是对的! 这在物联网、嵌入式开发环境特别常见,尤其是开发板、树莓派、rk3588 这类设备。 解决方法: 加硬件…...
