【蓝桥杯集训·每日一题】AcWing 1249. 亲戚
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- 并查集
一、题目
1、原题链接
1249. 亲戚
2、题目描述
或许你并不知道,你的某个朋友是你的亲戚。
他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。
如果能得到完整的家谱,判断两个人是否是亲戚应该是可行的,但如果两个人的最近公共祖先与他们相隔好几代,使得家谱十分庞大,那么检验亲戚关系实非人力所能及。
在这种情况下,最好的帮手就是计算机。
为了将问题简化,你将得到一些亲戚关系的信息,如Marry和Tom是亲戚,Tom和Ben是亲戚,等等。
从这些信息中,你可以推出Marry和Ben是亲戚。
请写一个程序,对于我们的关于亲戚关系的提问,以最快的速度给出答案。
输入格式
输入由两部分组成。
第一部分以 N,M 开始。N 为问题涉及的人的个数。这些人的编号为 1,2,3,…,N。下面有 M 行,每行有两个数 ai,bi,表示已知
ai 和 bi 是亲戚。第二部分以 Q 开始。以下 Q 行有 Q 个询问,每行为 ci,di ,表示询问 ci 和 di 是否为亲戚。
输出格式
对于每个询问 ci,di,输出一行:若 ci 和 di 为亲戚,则输出
Yes,否则输出No。数据范围
1≤N≤20000,1≤M≤106,1≤Q≤106
输入样例:
10 7 2 4 5 7 1 3 8 9 1 2 5 6 2 3 3 3 4 7 10 8 9输出样例:
Yes No Yes
二、解题报告
1、思路分析
(1)利用并查集,将所有互为亲戚的合并为同一个集合。
(2)通过查找两个结点的祖宗结点是否相同来判断两人是否为亲戚。
(3)并查集模板题,注意细节,并且此题使用cin、cout会超时,应使用scanf、printf或puts进行输入输出。
2、时间复杂度
时间复杂度为O(n)
3、代码详解
#include <iostream>
using namespace std;
const int N=20010;
int n,m;
int p[N]; //p[]存储每个结点的祖宗结点
//查找操作,返回x的祖宗结点
int find(int x){if(p[x]!=x) p[x]=find(p[x]); //如果p[x]不是祖宗的话,递归查找x的祖宗return p[x]; //直到找到x的祖宗,返回
}
int main(){scanf("%d%d",&n,&m); //使用cin、cout会TLE//初始化,每个结点的祖宗为自身for(int i=1;i<=n;i++){p[i]=i;}while(m--){int a,b;scanf("%d%d",&a,&b);if(find(a)==find(b)) continue;p[find(b)]=find(a); //a,b的祖宗结点不同,则合并}int q;cin>>q;while(q--){int c,d;scanf("%d%d",&c,&d);if(find(c)==find(d)) puts("Yes"); //祖宗相同输出Yes,否则输出Noelse puts("No");}return 0;
}
三、知识风暴
并查集
- 并查集主要用于处理一些不相交集合的合并问题。
- 具体操作可以参考我的这篇博客点击这里的“知识风暴”模块。
相关文章:

【蓝桥杯集训·每日一题】AcWing 1249. 亲戚
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴并查集一、题目 1、原题链接 1249. 亲戚 2、题目描述 或许你并不知道,你的某个朋友是你的亲戚。 他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。 如果…...

iphone所有机型的屏幕尺寸
手机设备型号屏幕尺寸(吋)分辨率点数(pt)屏幕显示模式分辨率像素(px)屏幕比例iPhone SE4.03205682x640113616:9iPhone 6/6s/7/8/SE 24.73756672x750133416:9iPhone 6P/7P/8P5.54147363x1242220816:9iPhone XR/116.14148962x828179219.5:9iPhone X/XS/11P5.83758123x1125243619.…...
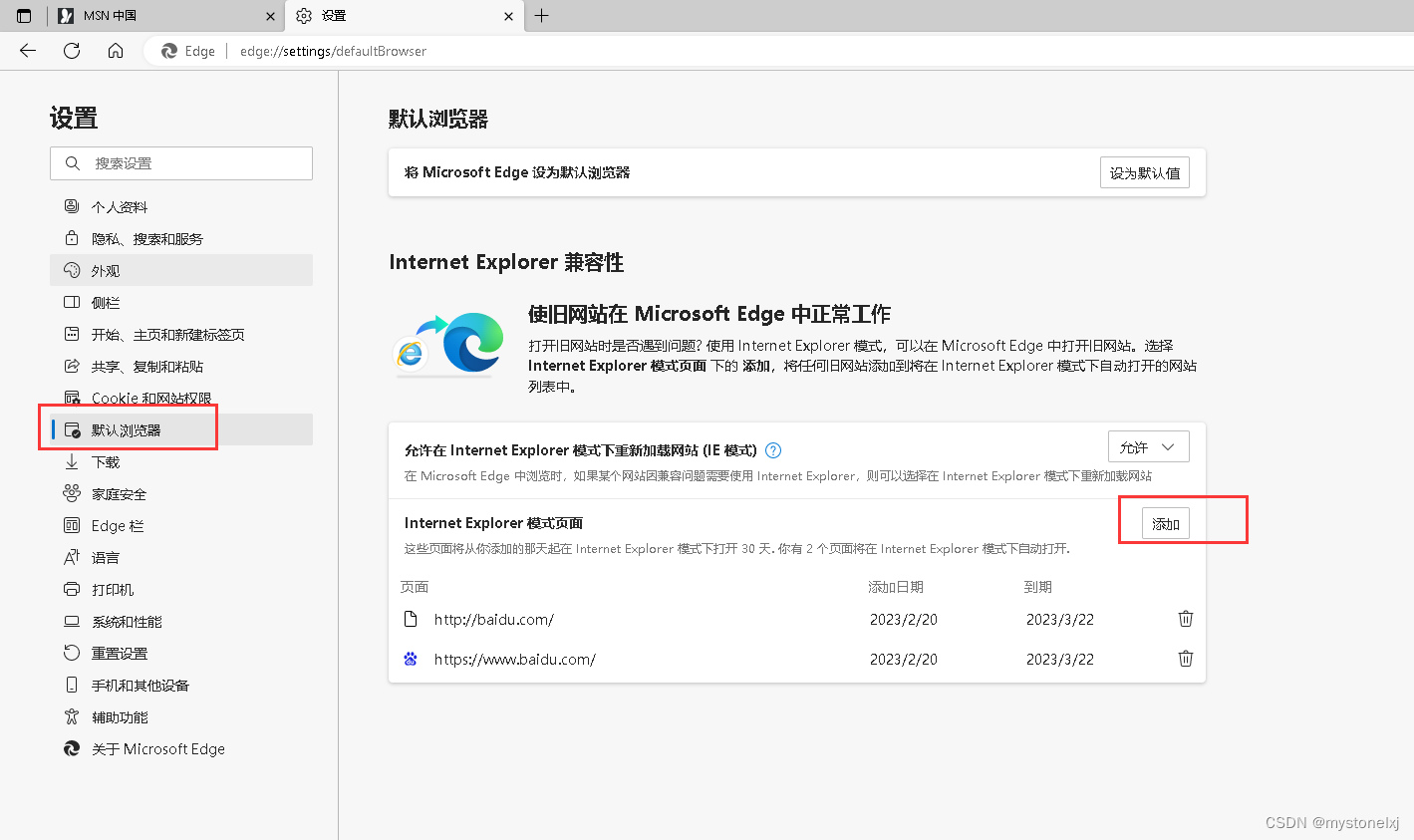
Windows10使用-处理IE自动跳转至Edge
文章目录 前言一、调整Edge二、调整Internet选项三、搜索栏的恢复总结前言 微软官方宣布,自2023年2月14日永久停止支持Internet Explorer 11浏览器。后期点击IE 图标将会自动跳转到Edge界面。对于一些网站,可能需要使用IE模式才能正常使用,这时候就需要做相应的调整,才能够…...
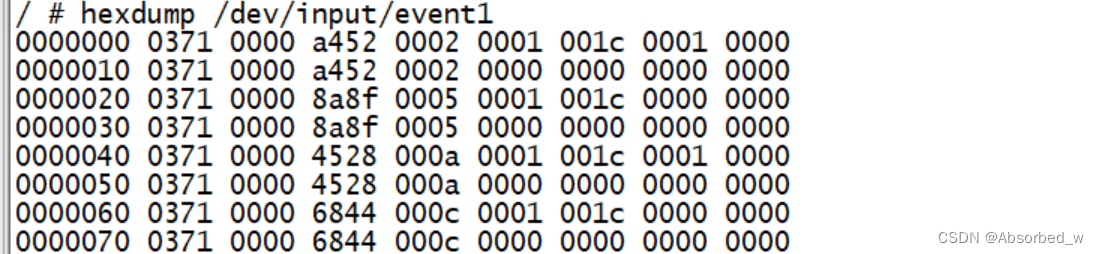
linux input子系统,gpio-keys,gpio中断使用
GPIO控制 嵌入式linux下应用编程会经常使用到gpio,GPIO 可以通过 sysfs 方式进行操控,进入到/sys/class/gpio 目录下,如下所示: 可以看到该目录下包含两个文件 export、 unexport 以及 5 个 gpiochipX(X 等于 0、 32、…...

分析称勒索攻击在非洲、中东与中国增长最快
Orange Cyberdefense(OCD)于 2022 年 12 月 1 日发布了最新的网络威胁年度报告。报告中指出,网络勒索仍然是头号威胁 ,也逐渐泛滥到世界各地。 报告中的网络威胁指的是企业网络中的某些资产被包括勒索软件在内的攻击进行勒索&…...

ArcPy批量合并矢量shape文件
当有大量矢量(.shp)格式文件需要合并成一个矢量文件时,可以考虑使用 ArcPy 进行批量合并,代码如下: # coding:utf-8 import os import arcpy from arcpy import envenv.workspace "C:/Users/Desktop/demo"…...

改写有序表的题目核心点
1、核心点 1)分析增加什么数据项可以支持题目 2)有序表一定要保持内部参与排序的key不重复 【补充说明:要存储重复的key值,要么将相同的key压在一起,要么将每个key再封装一层,用内存地址区分】 3&#…...
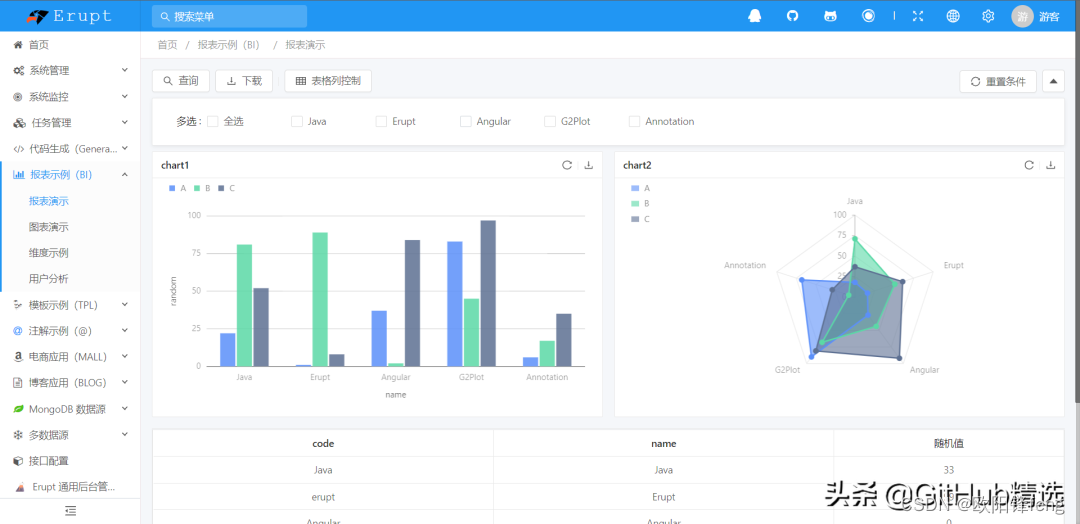
收藏这几个开源管理系统做项目,领导看了直呼牛X!
项目SCUI Admin 中后台前端解决方案Vue .NetCore 前后端分离的快速发开框架next-admin 适配移动端、pc的后台模板django-vue-admin-pro 快速开发平台Admin.NET 通用管理平台RuoYi 若依权限管理系统Vue3.2 Element-Plus 后台管理框架Pig RABC权限管理系统zheng 分布式敏捷开发…...
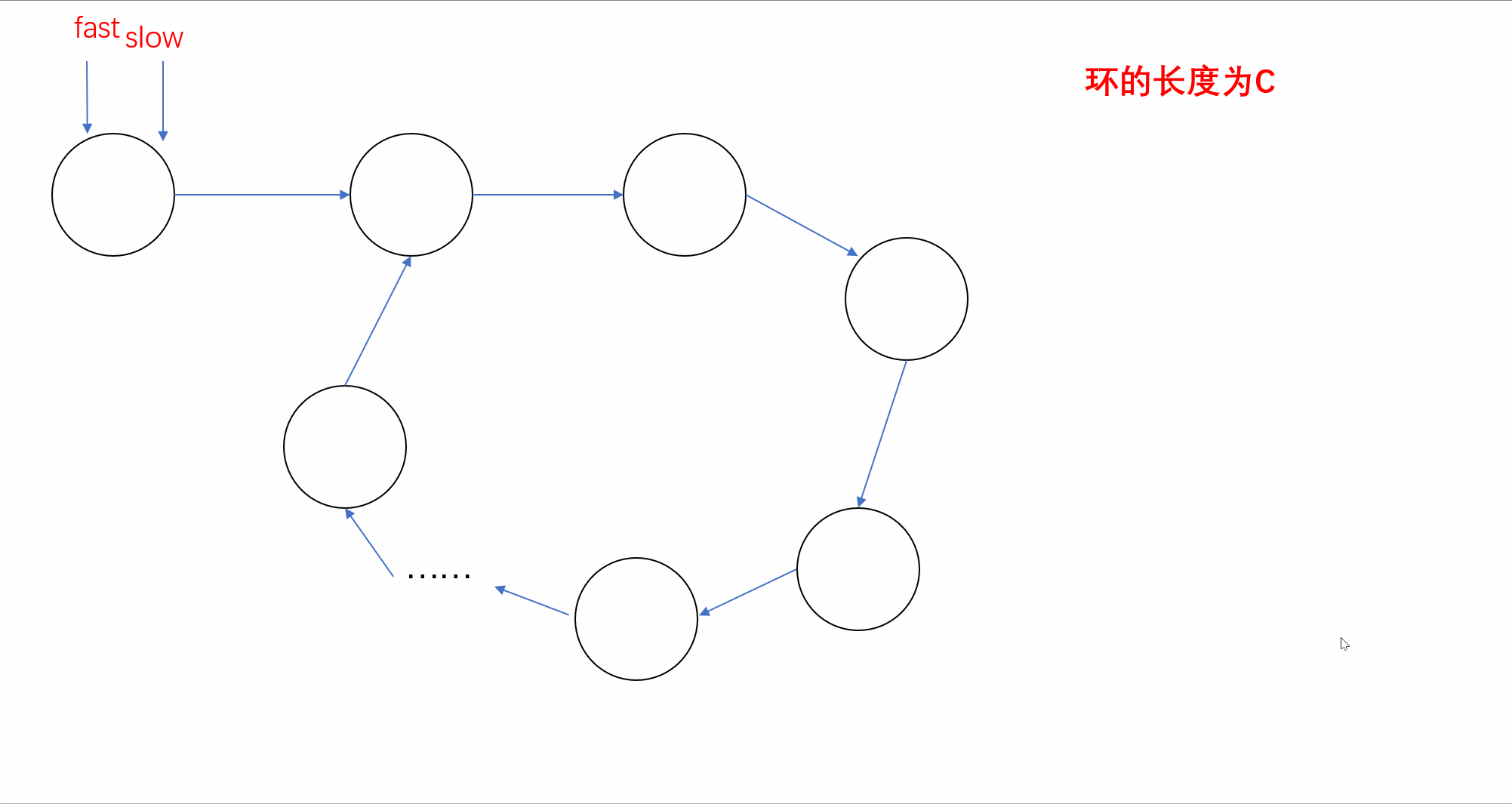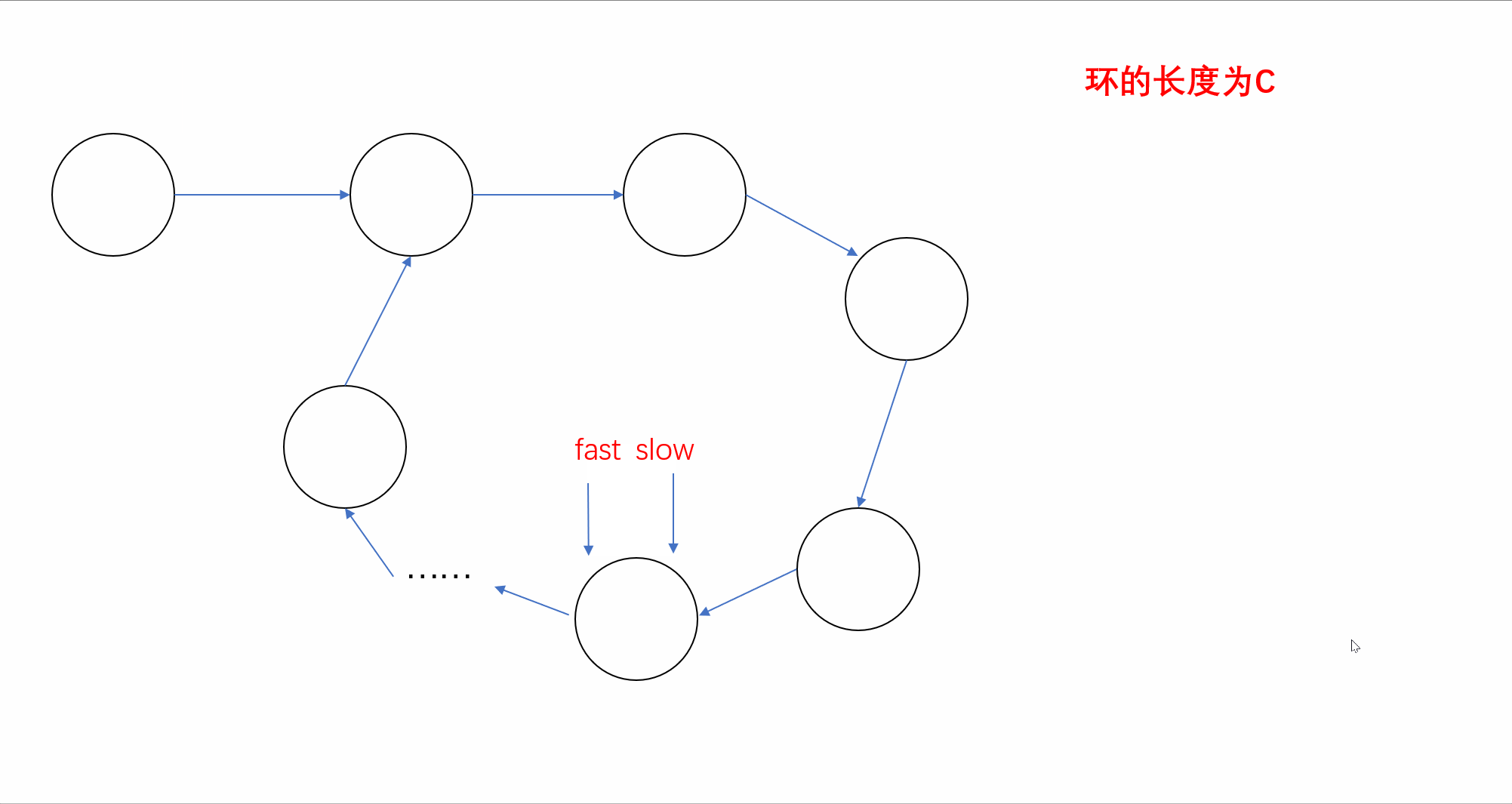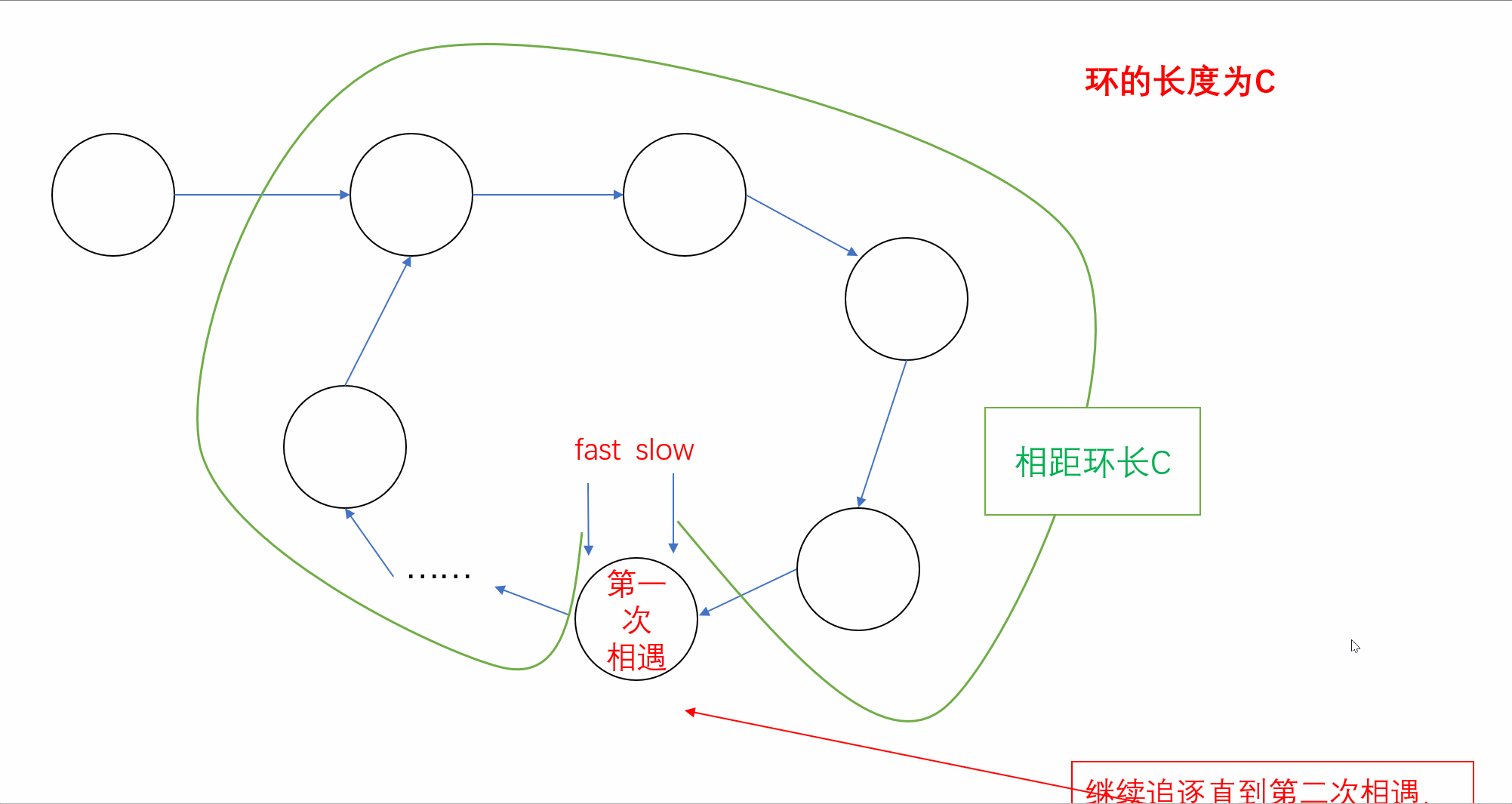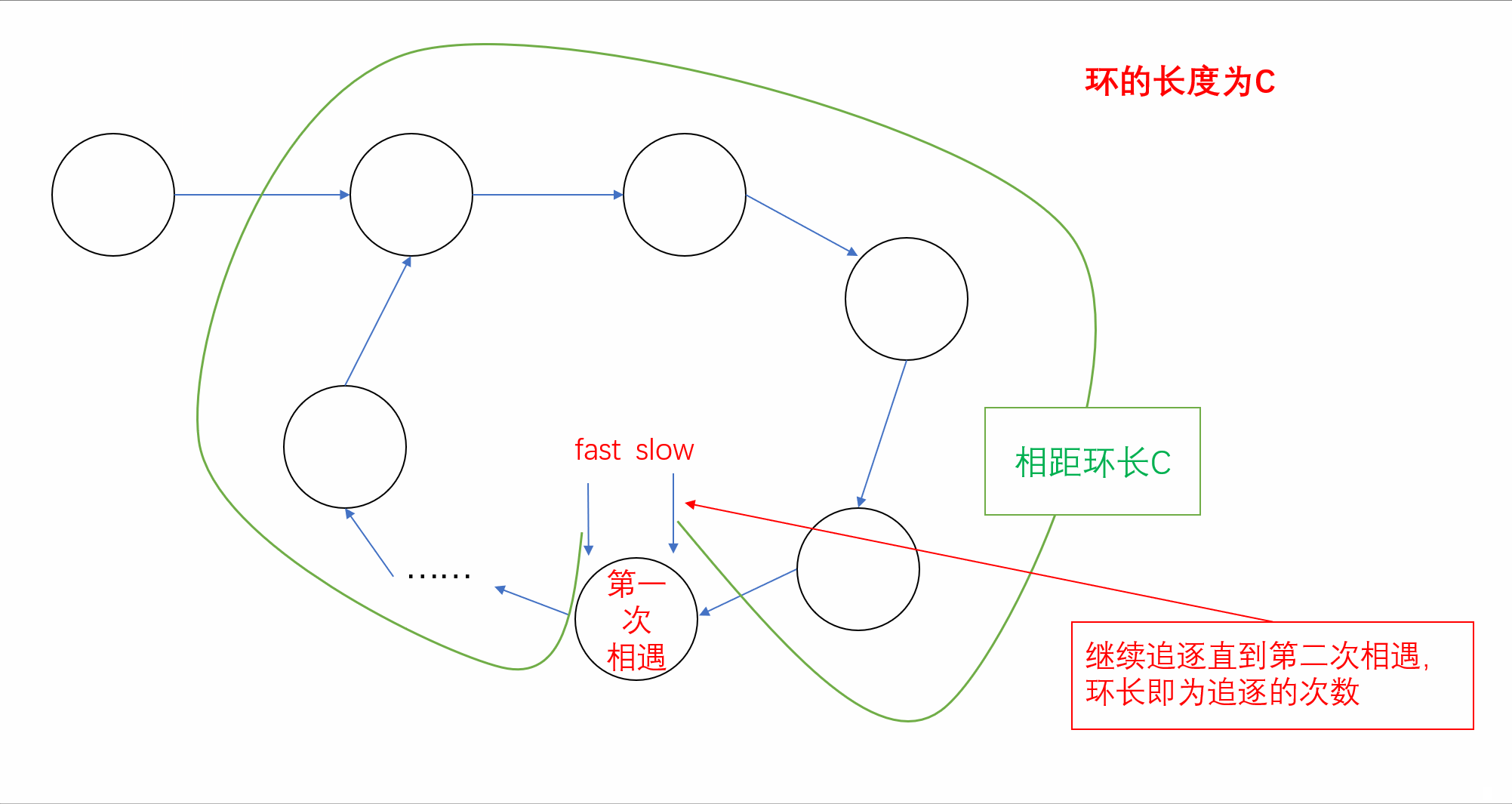
【刷题篇】链表(下)
前言🌸各位读者们好,本期我们来填填之前留下的坑,继续来讲解几道和链表相关的OJ题。但和上期单向链表不一样的是,我们今天的题目主要是于环形链表有关,下面让我们一起看看吧。💻本期的题目有:环…...
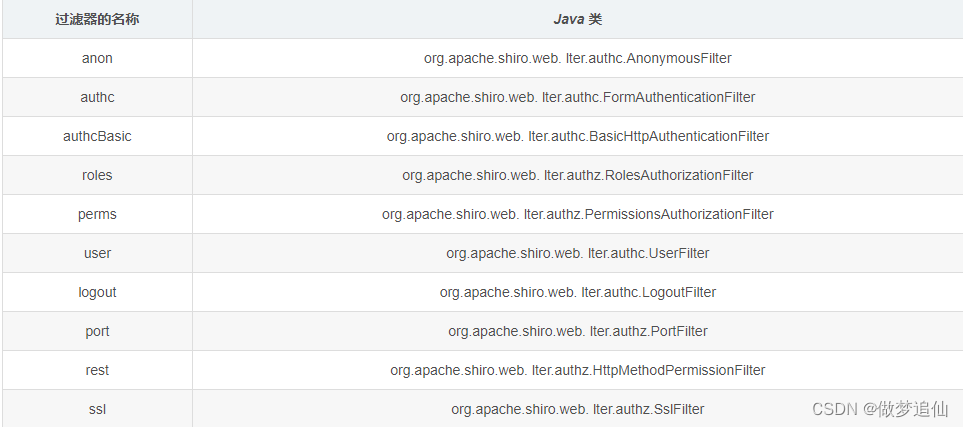
Shiro
Shiro 1.权限管理概述 2.Shiro权限框架 2.1 概念 2.2 Apache Shiro 与Spring Security区别 3.Shiro认证 3.1 基于ini认证 3.2 自定义Realm --认证 4.Shiro授权 4.1 基于ini授权 4.2 自定义realm – 授权 5.项目集成shiro 认证-授权注意点 5.1 认证…...
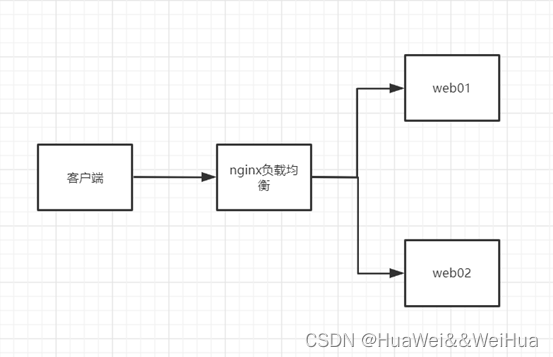
使用nginx进行负载均衡配置详细说明
使用nginx进行负载均衡 1. nginx负载均衡介绍 nginx应用场景之一就是负载均衡。在访问量较多的时候,可以通过负载均衡,将多个请求分摊到多台服务器上,相当于把一台服务器需要承担的负载量交给多台服务器处理,进而提高系统的吞吐…...

N皇后问题
#include<iostream> #include<string> #include<vector> using namespace std; #define MAX 20//最大20个皇后 int n ;//实际皇后个数 int sum ;//答案个数 vector<vector<int>> attack(MAX, vector<int>(MAX, 0));//标记攻击位置 vector&…...

强化学习DQN之俄罗斯方块
强化学习DQN之俄罗斯方块强化学习DQN之俄罗斯方块算法流程文件目录结构模型结构游戏环境训练代码测试代码结果展示强化学习DQN之俄罗斯方块 算法流程 本项目目的是训练一个基于深度强化学习的俄罗斯方块。具体来说,这个代码通过以下步骤实现训练: 首先…...

1.3总线:并行总线、串行总线、单工、半双工、全双工、总线宽度、总线带宽、总线的分类、数据总线、地址总线、控制总线
1.3总线:并行总线、串行总线、单工、半双工、全双工、总线宽度、总线带宽、总线的分类、数据总线、地址总线、控制总线总线并行总线、串行总线单工、半双工、全双工总线宽度总线带宽总线的分类数据总线(Data Bus,DB)地址总线&…...

Linux驱动开发—设备树开发详解
设备树开发详解 设备树概念 Device Tree是一种描述硬件的数据结构,以便于操作系统的内核可以管理和使用这些硬件,包括CPU或CPU,内存,总线和其他一些外设。 Linux内核从3.x版本之后开始支持使用设备树,可以实现驱动代…...

深入浅出C++ ——继承
文章目录一、继承的相关概念1. 继承的概念2. 继承格式3. 继承方式4. 访问限定符5. 继承基类成员访问方式的变化二、基类和派生类对象赋值转换三、继承中的作用域四、派生类的默认成员函数五、继承与友元六、继承与静态成员七、菱形继承及菱形虚拟继承1. 单继承2. 多继承3. 菱形…...
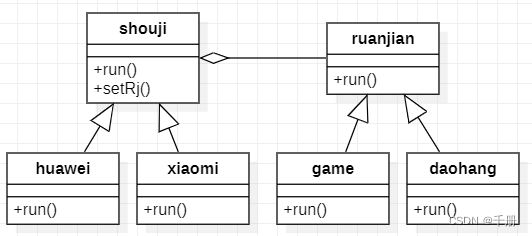
设计模式C++实现20: 桥接模式(Bridge)
部分内容参考大话设计模式第22章;本实验通过C语言实现。 一 基本原理 意图:将抽象部分和实现部分分离,使它们都可以独立变化。 上下文:某些类型由于自身的逻辑,具有两个或多个维度的变化。如何应对“多维度的变化”…...

Android中的Rxjava
要使用Rxjava首先要导入两个包,其中rxandroid是rxjava在android中的扩展 implementation io.reactivex:rxandroid:1.2.1implementation io.reactivex:rxjava:1.2.0observer 是一个观察者接口,泛型T为观察者观察数据的类型,里面只有三个方法&a…...

【RocketMQ】源码详解:消息储存服务加载、文件恢复、异常恢复
消息储存服务加载 入口:org.apache.rocketmq.store.DefaultMessageStore#load 在创建brokerContriller时会调用初始化方法初始化brokerController,在初始化方法中会进行消息储存服务的加载 this.messageStore.load(); 加载方法主要是加载一些必要的参数和数据,如配…...

数字IC设计工程师是做什么的?
随着我国半导体产业的发展,近几年的新入行的从业人员,除了微电子相关专业的,还有就是物理、机械、数学、计算机等专业,很多人对这一高薪行业充满了好奇,那么数字IC设计工程师到底是做什么的? 首先来看看数…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
