改写有序表的题目核心点
1、核心点
1)分析增加什么数据项可以支持题目
2)有序表一定要保持内部参与排序的key不重复
【补充说明:要存储重复的key值,要么将相同的key压在一起,要么将每个key再封装一层,用内存地址区分】
3)增加这个数据项了,在平衡性调整时,保证这个数据项也能更新正确
4)做到上面3点,剩下就是搜索二叉树怎么实现想要的接口的问题了
2、浅谈红黑树
红黑树的五个条件:
- 每个节点非黑即红;
- 根节点是黑色;
- 叶节点(NIL)是黑色【虚拟空节点,并不是看得见的叶子节点】
- 如果一个节点是红色,则它的两个子节点是黑色的;
- 从根节点触发到所有叶节点的路径上,黑色节点数量相同。
先回忆AVL树和SB树的平衡条件:
- AVL树左右子树的高度差不超过1,是非常严苛的平衡;
- SB树中每棵子树的大小不小于其兄弟的子树大小,其实质就是保证了较少节点的子树和较多节点的子树的节点数量差不超过两倍,是模糊的平衡性。
而结合红黑树的第4和5个条件,也就是红黑树最长路径和最短路径之间的关系是:最长路径=2×最短路径最长路径 = 2 \times 最短路径最长路径=2×最短路径
可见,红黑树本质上也是用树高来控制平衡,但是相比AVL树控制得更松散,依然是模糊的平衡性,目的和SB树一样,减少频繁地调整,内存IO消耗较低。
了解了之前AVL树和SB树的平衡调整,红黑树的平衡调整也是类似的。
相关文章:

改写有序表的题目核心点
1、核心点 1)分析增加什么数据项可以支持题目 2)有序表一定要保持内部参与排序的key不重复 【补充说明:要存储重复的key值,要么将相同的key压在一起,要么将每个key再封装一层,用内存地址区分】 3&#…...
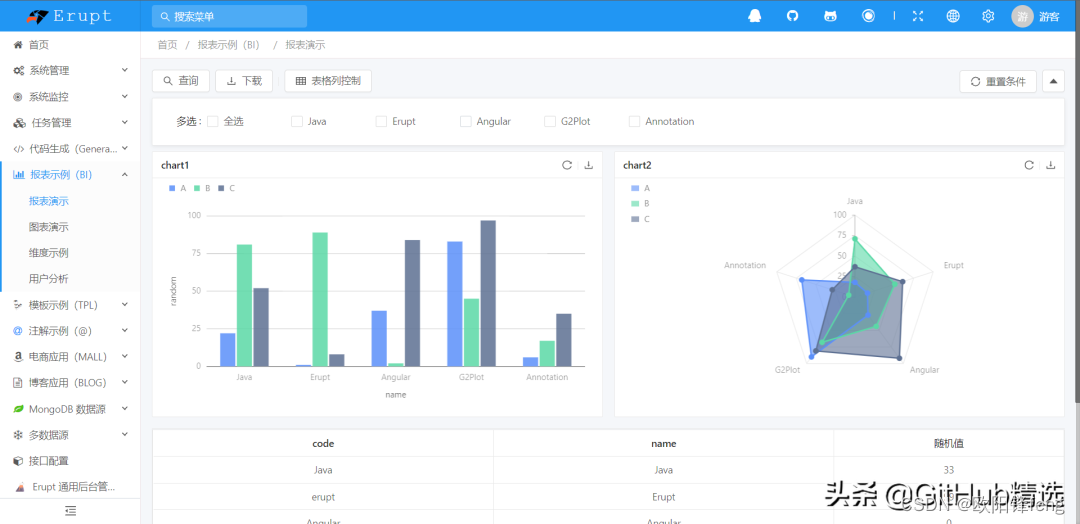
收藏这几个开源管理系统做项目,领导看了直呼牛X!
项目SCUI Admin 中后台前端解决方案Vue .NetCore 前后端分离的快速发开框架next-admin 适配移动端、pc的后台模板django-vue-admin-pro 快速开发平台Admin.NET 通用管理平台RuoYi 若依权限管理系统Vue3.2 Element-Plus 后台管理框架Pig RABC权限管理系统zheng 分布式敏捷开发…...
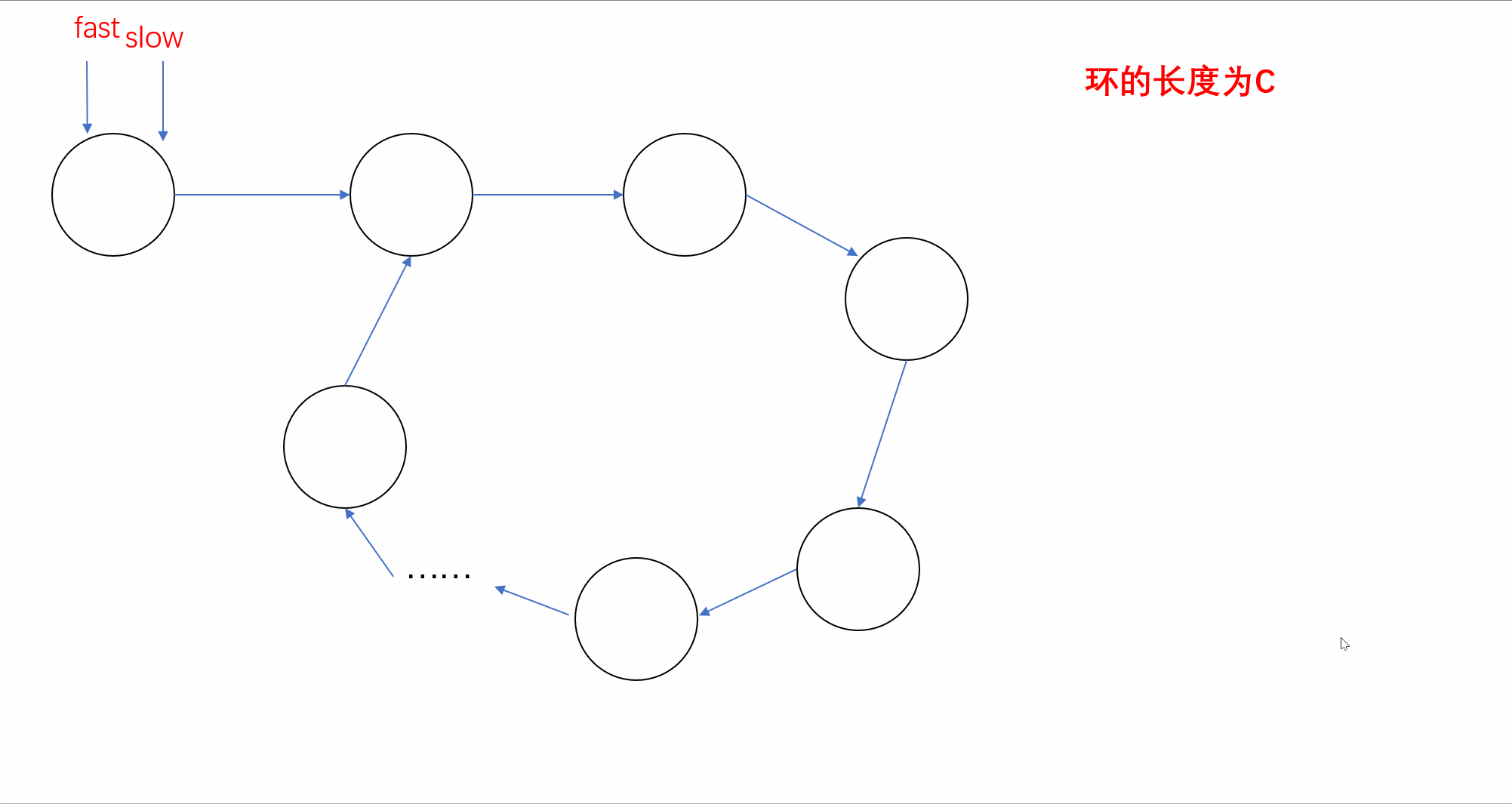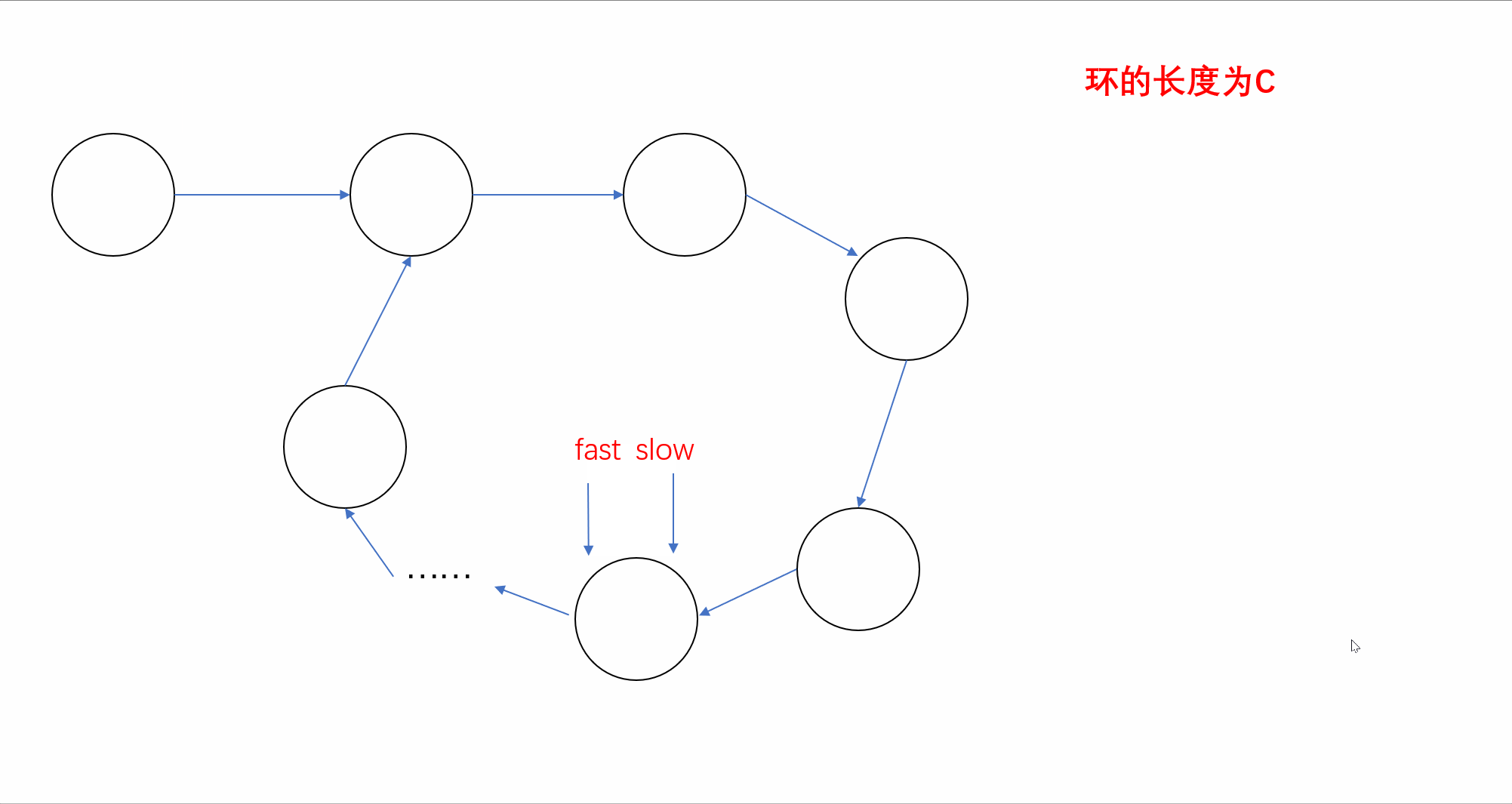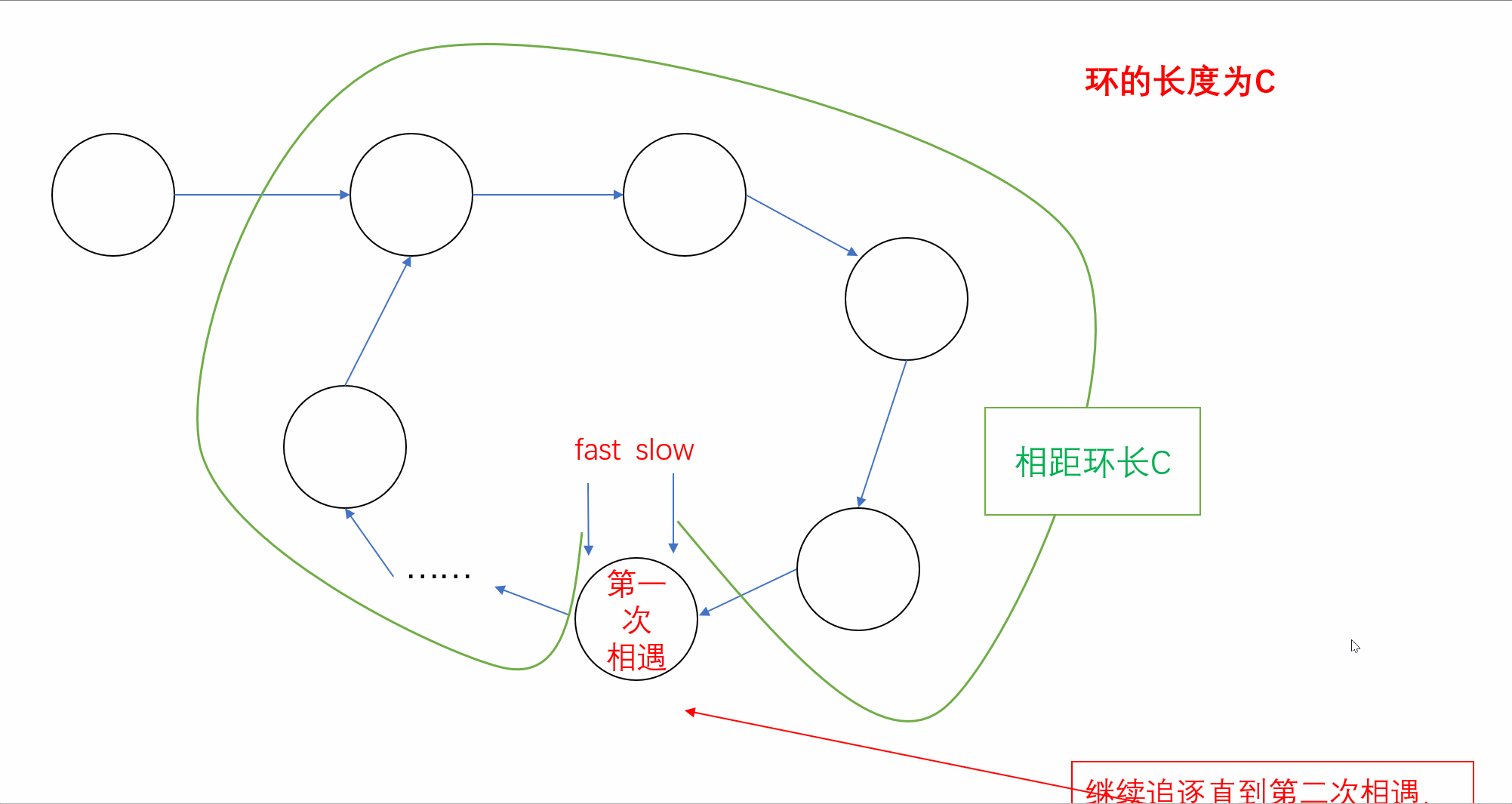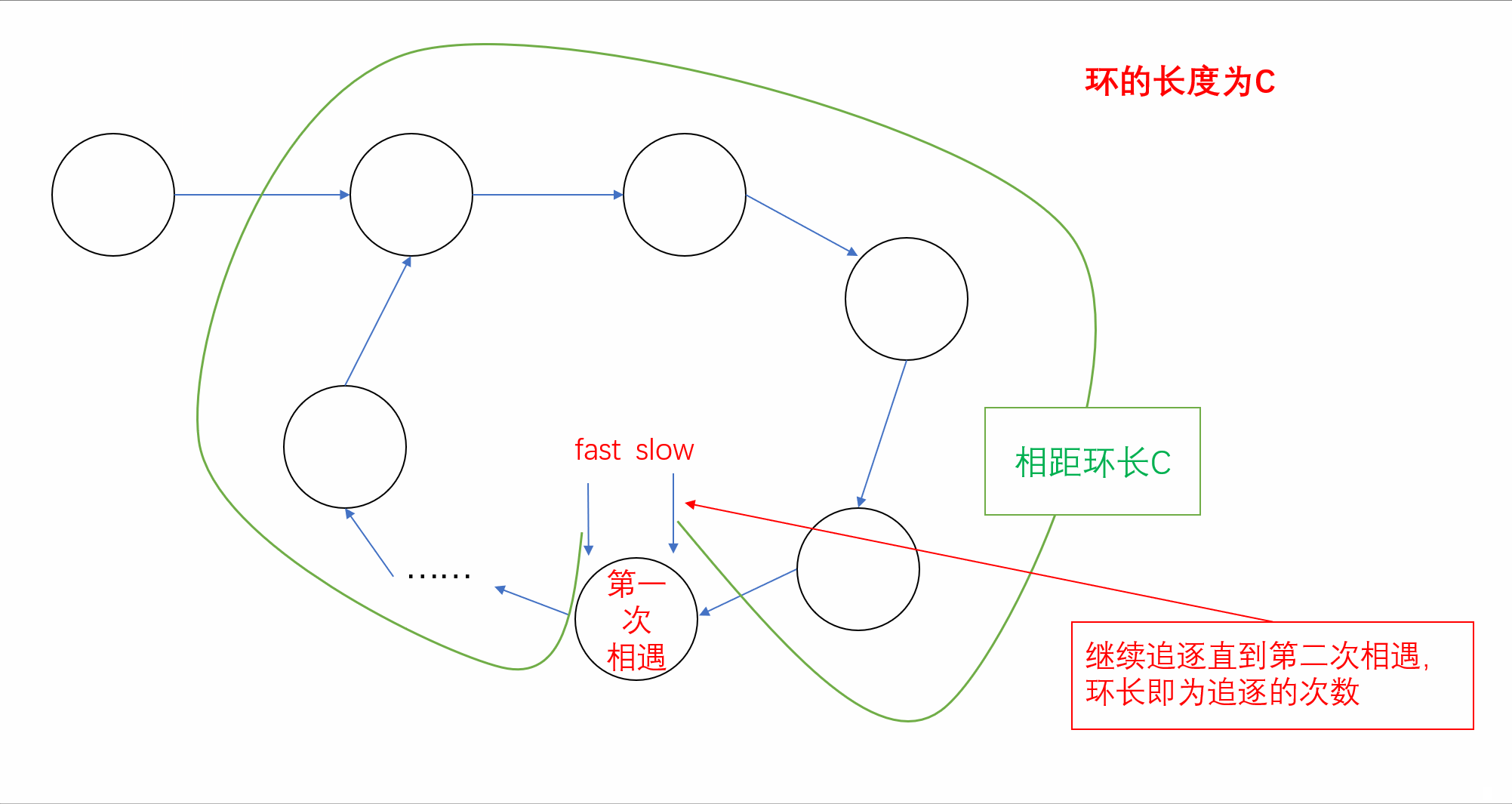
【刷题篇】链表(下)
前言🌸各位读者们好,本期我们来填填之前留下的坑,继续来讲解几道和链表相关的OJ题。但和上期单向链表不一样的是,我们今天的题目主要是于环形链表有关,下面让我们一起看看吧。💻本期的题目有:环…...
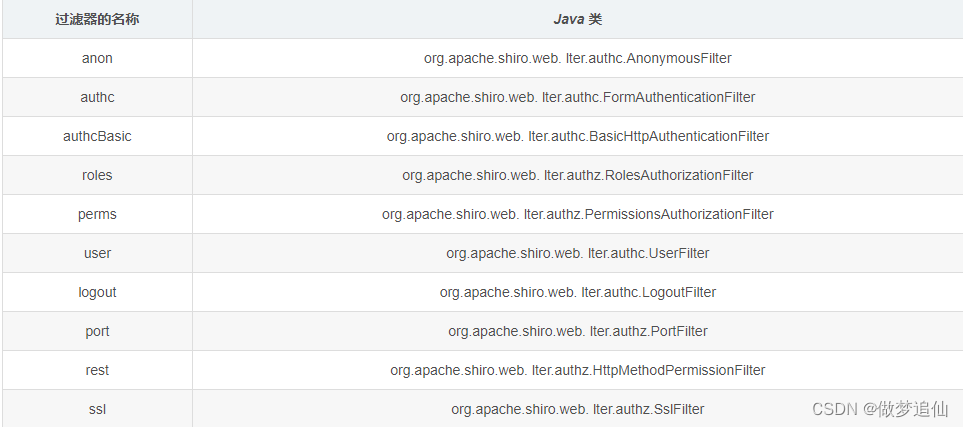
Shiro
Shiro 1.权限管理概述 2.Shiro权限框架 2.1 概念 2.2 Apache Shiro 与Spring Security区别 3.Shiro认证 3.1 基于ini认证 3.2 自定义Realm --认证 4.Shiro授权 4.1 基于ini授权 4.2 自定义realm – 授权 5.项目集成shiro 认证-授权注意点 5.1 认证…...
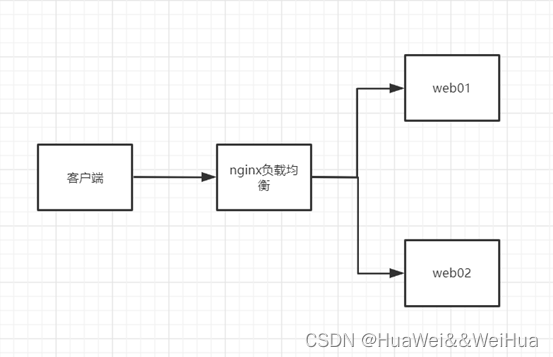
使用nginx进行负载均衡配置详细说明
使用nginx进行负载均衡 1. nginx负载均衡介绍 nginx应用场景之一就是负载均衡。在访问量较多的时候,可以通过负载均衡,将多个请求分摊到多台服务器上,相当于把一台服务器需要承担的负载量交给多台服务器处理,进而提高系统的吞吐…...

N皇后问题
#include<iostream> #include<string> #include<vector> using namespace std; #define MAX 20//最大20个皇后 int n ;//实际皇后个数 int sum ;//答案个数 vector<vector<int>> attack(MAX, vector<int>(MAX, 0));//标记攻击位置 vector&…...

强化学习DQN之俄罗斯方块
强化学习DQN之俄罗斯方块强化学习DQN之俄罗斯方块算法流程文件目录结构模型结构游戏环境训练代码测试代码结果展示强化学习DQN之俄罗斯方块 算法流程 本项目目的是训练一个基于深度强化学习的俄罗斯方块。具体来说,这个代码通过以下步骤实现训练: 首先…...

1.3总线:并行总线、串行总线、单工、半双工、全双工、总线宽度、总线带宽、总线的分类、数据总线、地址总线、控制总线
1.3总线:并行总线、串行总线、单工、半双工、全双工、总线宽度、总线带宽、总线的分类、数据总线、地址总线、控制总线总线并行总线、串行总线单工、半双工、全双工总线宽度总线带宽总线的分类数据总线(Data Bus,DB)地址总线&…...

Linux驱动开发—设备树开发详解
设备树开发详解 设备树概念 Device Tree是一种描述硬件的数据结构,以便于操作系统的内核可以管理和使用这些硬件,包括CPU或CPU,内存,总线和其他一些外设。 Linux内核从3.x版本之后开始支持使用设备树,可以实现驱动代…...

深入浅出C++ ——继承
文章目录一、继承的相关概念1. 继承的概念2. 继承格式3. 继承方式4. 访问限定符5. 继承基类成员访问方式的变化二、基类和派生类对象赋值转换三、继承中的作用域四、派生类的默认成员函数五、继承与友元六、继承与静态成员七、菱形继承及菱形虚拟继承1. 单继承2. 多继承3. 菱形…...
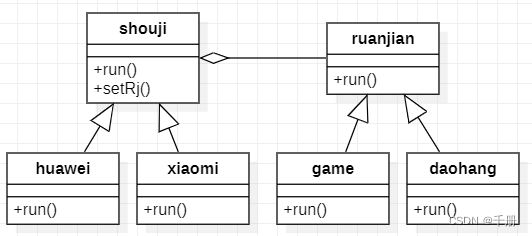
设计模式C++实现20: 桥接模式(Bridge)
部分内容参考大话设计模式第22章;本实验通过C语言实现。 一 基本原理 意图:将抽象部分和实现部分分离,使它们都可以独立变化。 上下文:某些类型由于自身的逻辑,具有两个或多个维度的变化。如何应对“多维度的变化”…...

Android中的Rxjava
要使用Rxjava首先要导入两个包,其中rxandroid是rxjava在android中的扩展 implementation io.reactivex:rxandroid:1.2.1implementation io.reactivex:rxjava:1.2.0observer 是一个观察者接口,泛型T为观察者观察数据的类型,里面只有三个方法&a…...

【RocketMQ】源码详解:消息储存服务加载、文件恢复、异常恢复
消息储存服务加载 入口:org.apache.rocketmq.store.DefaultMessageStore#load 在创建brokerContriller时会调用初始化方法初始化brokerController,在初始化方法中会进行消息储存服务的加载 this.messageStore.load(); 加载方法主要是加载一些必要的参数和数据,如配…...

数字IC设计工程师是做什么的?
随着我国半导体产业的发展,近几年的新入行的从业人员,除了微电子相关专业的,还有就是物理、机械、数学、计算机等专业,很多人对这一高薪行业充满了好奇,那么数字IC设计工程师到底是做什么的? 首先来看看数…...

【040】134. 加油站[简单模拟 + 逻辑转化]
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。 给定两个整数数组 gas 和 cost &am…...
Python用selenium实现自动登录和下单的脚本
前言 学python对selenium应该不陌生吧 Selenium 是最广泛使用的开源 Web UI(用户界面)自动化测试套件之一。Selenium 支持的语言包括C#,Java,Perl,PHP,Python 和 Ruby。目前,Selenium Web 驱动…...
Cartographer源码无死角解析-(55) 2D后端优化→AppendNode()、class MapById、 PoseGraphData、)
(02)Cartographer源码无死角解析-(55) 2D后端优化→AppendNode()、class MapById、 PoseGraphData、
讲解关于slam一系列文章汇总链接:史上最全slam从零开始,针对于本栏目讲解(02)Cartographer源码无死角解析-链接如下: (02)Cartographer源码无死角解析- (00)目录_最新无死角讲解:https://blog.csdn.net/weixin_43013761/article/details/127350885 文末正下方中心提供了本…...

如何在jmeter中把响应中的数据提取出来并引用
jmeter做接口测试过程中,经常遇到请求需要用到token的时候,我们可以把返回token的接口用后置处理器提取出来,但是在这种情况下,只能适用于当前的线程组,其他线程组无法引用到提取的token变量值,所以必须要生…...

2023环翠区编程挑战赛中学组题解
T1. 出栈序列 题目描述 栈是一种“先进后出”的数据结构,对于一个序列1,2,...,n1,2, ...,n1,2,...,n,其入栈顺序是1,2,...n1,2, ...n1,2,...n,但每个元素出栈的时机可以自由选择。 例如111入栈、111出栈,222入栈、333入栈、333…...

手撸一个Switch开关组件
一、前言 手撸系列又来了,这次咱们来撸一个Switch开关组件,废话不多说,咱们立刻发车。 二、使用效果 三、实现分析 首先我们先不想它的这个交互效果,我们就实现“不合格”时的一个静态页面,静态页面大致如下&#x…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
