数据结构与算法复杂度介绍
目录
一、基本概念
二、时间复杂度
【2.1】时间复杂度概念
【2.2】大O的渐进表示法
【2.3】举例时间复杂度计算
三、空间复杂度
一、基本概念
数据结构:相互之间存在一种或者多种特定关系的数据元素的集合。在逻辑上可以分为线性结构,散列结构、树形结构,图形结构等等。
算法:求解具体问题的步骤描述,代码上表现出来是解决特定问题的一组有限的指令序列。
算法复杂度:时间和空间复杂度,衡量算法效率,算法在执行过程中,随着数据规模n的增长,算法执行所花费的时间和空间的增长速度。
常见的时间复杂度:
| 表达式 | 大O表示法 | 方程 |
|---|---|---|
| 5201314 | O(1) | 常数阶 |
| 3n+4 | O(n) | 线性阶 |
| 3n^2+4n+5 | O(n^2) | 平方阶 |
| 3log(2)n+4 | O(logn) | 对数阶 |
| 2n+3nlog(2)n+14 | O(nlogn) | nLogn阶 |
| n^3+2n^2+4n+6 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
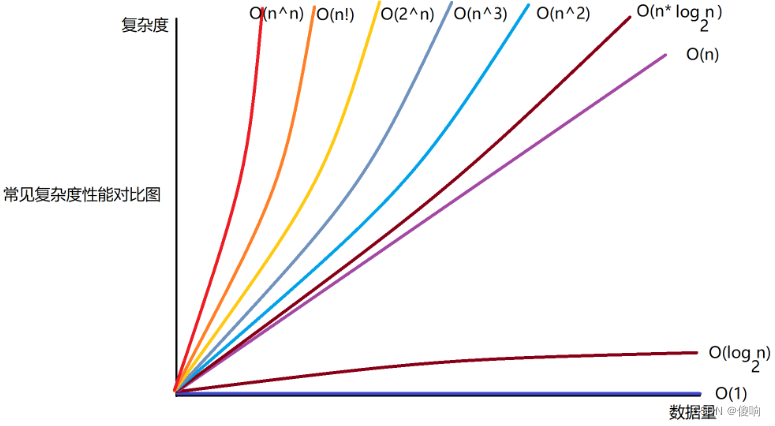
常见算法的时间复杂度关系:O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n!) < O(n^n)
【复杂度指标对比】
【创建的数据结构算法的复杂度】
| 大O计法 | 应用示例 |
|---|---|
| O(1) | 数组随机访问、哈希表 |
| O(logn) | 二分搜索、二叉堆调整、AVL、红黑树查找 |
| O(n) | 线性搜索 |
| O(nlogn) | 堆排序、快速排序、归并排序 |
| O(n^2) | 冒泡排序、选择排序、插入排序 |
| O(2^n) | 子集树 |
| O(n!) | 排列树 |
二、时间复杂度
【2.1】时间复杂度概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?
是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i) // 循环次数为N^2{for (int j = 0; j < N; ++j){++count;}}for (int i = 0; i < 2 * N; i++) // 循环次数为2 * N{++count;}int M = 10;while (M--) // 循环次数为10{++count;}printf("%d\n", count);
}
// Func1 执行的基本操作次数 :F(N) = (N^2) + (2 * N) + 10
// 比如:N = 10 F(N) = 130
// 比如:N = 100 F(N) = 10210
// 比如:N = 1000 F(N) = 1002010
// 上面N越大后面两项对整个表达式的影响是越来越小的
// 实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
// 最终以大概的次数:上面代码的时间复杂度是N^2【2.2】大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
【推导大O阶方法】
-
用常数1取代运行时间中的所有加法常数,O1并不代表是1次,而是代表是常数次。
-
在修改后的运行次数函数中,只保留最高阶项。
-
如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
【使用大O的渐进表示法以后,在推到一下Func1的时间复杂度为】
// Func1 执行的基本操作次数 :F(N) = (N^2) + (2 * N) + 10
// 比如:N = 10 F(N) = 130
// 比如:N = 100 F(N) = 10210
// 比如:N = 1000 F(N) = 1002010
// 结果:去掉(2*N)去掉(10) -> 时间复杂度是N^2通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数,另外有些算法的时间复杂度存在最好、平均和最坏情况:
-
最坏情况:任意输入规模的最大运行次数(上界)。
-
平均情况:任意输入规模的期望运行次数。
-
最好情况:任意输入规模的最小运行次数(下界)。
-
例如:在一个长度为N数组中搜索一个数据x。
-
最好情况:1次找到。
-
最坏情况:N次找到。
-
平均情况:N/2次找到。
在实际中一般情况关注的是算法的最坏运行情况!
【2.3】举例时间复杂度计算
【实例】
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k)// 循环次数:2 * N{++count;}int M = 10;while (M--) // // 循环次数:10{++count;}printf("%d\n", count);
}
// 正常为:(2 * N) + 10
// 在此:10 影响不大, 2为固定值影响不大,影响时间复杂度的是N
// 以大O表示法:O(N)【实例】
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k) // 循环次数为:M次{++count;}for (int k = 0; k < N; ++k) // 循环次数为:N次{++count;}printf("%d\n", count);
}
// 正常为:M + N
// 在此:M 和 N 的准确值都是不知道的,所以都算在时间复杂度成员里
// 以大O表示法:O(M + N)【实例】
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k) // 循环次数为:100次{++count;}printf("%d\n", count);
}
// 正常为:100次
// 在此:N 没有参与任何东西
// 以大O表示法:O(1)【实例】
// 计算strchr的时间复杂度?
const char * strchr(const char * str, int character); // O(N)【实例】
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end) // 循环次数为:等差数列{ // N-1 N-2 N-3 N-4.... -> 1+2+3+N-1 = N(N-1)/2int exchange = 0;for (size_t i = 1; i < end; ++i) {if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
// 正常为:
// 在此:实例5基本操作执行最好N次,最坏执行了(N*(N+1)/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N ^ 2)
// 以大O表示法:O(N^2)这是最坏的情况加
// 最好的情况下是O(N)【实例】
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x) // O(N * Log(2)n)
{assert(a);int begin = 0;int end = n - 1;while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}【实例】
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N) // O(N)
{if (0 == N)return 1;return Fac(N - 1)*N;
}【实例】
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N) // O(2^N) -> 斐波那契数相当于是一个很垃圾的算法
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
} // 优化
long long Fac(size_t N)
{if (N < 3)return 1;long long f1 = 1, f2 = 1, f3;for (size_t i = 3; i <= N; i++){f3 = f1 + f2;// 迭代f1 = f2;f2 = f3;}return f3;
}三、空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
【实例】
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n) // 常数个额外空间,所以空间复杂度为 O(1)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}【实例】
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n) // 动态开辟了N个空间,空间复杂度为 O(N)
{if (n == 0){return NULL;}long long * fibArray = (long long *)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}【实例】
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N) // 递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}相关文章:

数据结构与算法复杂度介绍
目录 一、基本概念 二、时间复杂度 【2.1】时间复杂度概念 【2.2】大O的渐进表示法 【2.3】举例时间复杂度计算 三、空间复杂度 一、基本概念 数据结构:相互之间存在一种或者多种特定关系的数据元素的集合。在逻辑上可以分为线性结构,散列结构、树…...

CentOS 安装蒲公英
官方教程链接: https://service.oray.com/question/5063.html 教程使用的是2.3版本,官网下载的最新版是2.4,所以命令会有所不同 安装成功后, 任意路径下执行pgyvisitor,调出交互界面pgyvisitor login,登录…...

英语语法基础--思维导图
思维导图通常用于可视化和整理信息,而英文语法非常广泛且复杂,无法在一个简单的思维导图中完整表示。然而,我可以提供一个简化版本的英文语法思维导图,列出一些主要的语法概念和部分示例。 请注意,这只是一个基本的概…...

Android泛型详解
参考文献:https://pingfangx.github.io/java-tutorials/java/generics/types.html 1,什么是泛型? Java泛型(generics)是JDK5中引入的一个新特性,泛型提供了 编译时类型安全检测机制, 该机制允许程序员在编译时检测到…...
C++信息学奥赛1178:成绩排序
#include<bits/stdc.h> using namespace std; int main(){int n;cin>>n; // 输入整数 n,表示数组的大小int arr[n]; // 创建大小为 n 的整型数组 arrstring brr[n]; // 创建大小为 n 的字符串数组 brrfor(int i0;i<n;i) cin>>brr[i]>>ar…...
)
【计算机视觉 | 目标检测】目标检测常用数据集及其介绍(七)
文章目录 一、Cops-Ref二、FAT (Falling Things)三、GEN1 Detection (Prophesee GEN1 Automotive Detection Dataset)四、RIT-18五、AGAR (Annotated Germs for Automated Recognition)六、EuroCity Persons七、Freiburg Groceries八、Lytro Illum九、PFN-PIC (PFN Picking Ins…...

100天精通Golang(基础入门篇)——第20天:Golang 接口 深度解析☞从基础到高级
🌷🍁 博主猫头虎🐅🐾 带您进入 Golang 语言的新世界✨✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文并茂…...

ESXi 6.7添加螃蟹2.5g网卡支持
安装了ESXi 6.7,结果机器两块网卡只能识别一块,然后想着不能让另一块浪费啊,开始折腾,看着网上都是找的驱动然后封装进iso,可是我已经装完了,怎么办,然后找到了下面解决方法 1.找驱动 下载RTL81…...

机器学习笔记之最优化理论与方法(四) 凸函数:定义与基本性质
机器学习笔记之最优化理论与方法——再回首:凸函数定义与基本性质 引言凸函数的定义严格凸函数凸函数的推论:凹函数 常见凸函数凸函数的基本性质几种保持函数凸性的运算凸集与凸函数之间的关联关系 引言 本节将介绍凸函数定义及其基本性质。 本文是关于…...

【Git】git tag 查看版本号 | 删除本地 | 删除远程仓库| 批量删除
一、删除指定tag 使用场景:比如我们在本地git tag了一个错误的版本号,但是还没有push,想直接删掉避免污染远程仓库 1、删除指令 要删除指定的Git标签(版本号),您可以使用以下命令: git tag -d 标…...
)
thinkphp:数据库查询,嵌套别的表的查询(别的表做子查询)
例子 从 vendors 表中选择记录。在 vendors 表中,筛选出具有满足以下条件的 vendor_code 值: 对应的采购订单(在 po_headers_all 表中)存在未完全接收的采购行(在 po_lines_all 表中)。相应的采购订单状态…...

《Linux 系统命令及Shell脚本实践指南》
Linux 系统命令及Shell脚本实践指南 《Linux 系统命令及Shell脚本实践指南》该书从结构上分为三部分:第一部分1.1Linux的历史发展1.2用户管理1.3任务管理单一时刻执行一次任务使用at周期性任务使用:cron表达式,命令crontab 1.4文件管理1.4.1 Linux shell…...

代码随想录算法训练营第三十八天 | ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
题目链接:509. 斐波那契数 代码随想录 视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili 看完代码随想录之后的想法: 我们要知道动态规划的五部曲; 1,确定dp数组的含义&#x…...
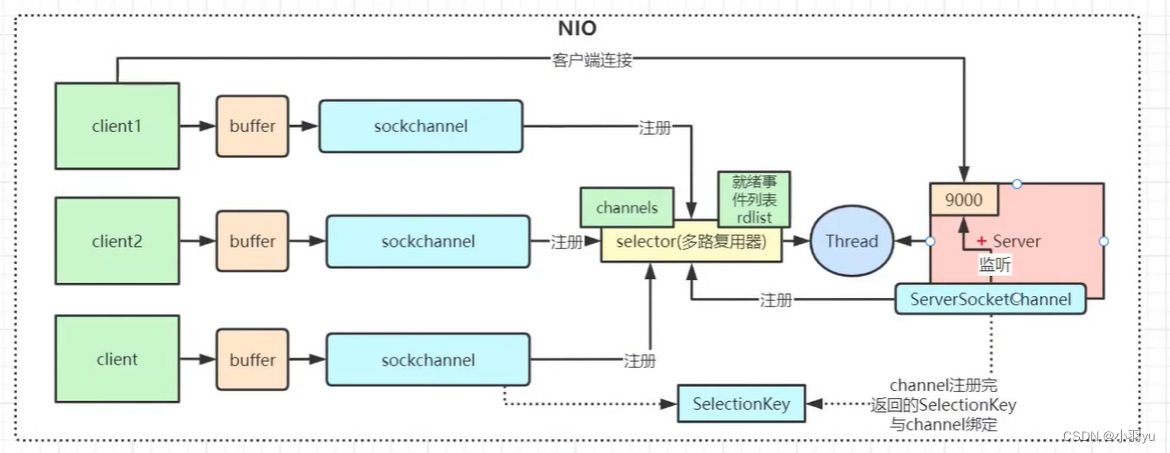
Java分别用BIO、NIO实现简单的客户端服务器通信
分别用BIO、NIO实现客户端服务器通信 BIONIONIO演示(无Selector)NIO演示(Selector) 前言: Java I/O模型发展以及Netty网络模型的设计思想 BIO Java BIO是Java平台上的BIO(Blocking I/O)模型&a…...

React Portals
什么是React Portals React Portals(React 门户)是 React 提供的一种机制,用于将组件渲染到 DOM 树中的不同位置,而不受组件层次结构的限制。它允许你将一个组件的渲染内容“传送”到 DOM 结构中的任何位置,通常用于处…...

Python基础之高级函数
异常捕获 Python中,使用trycatch两个关键字来实现对异常的处理。在我们平时的工作中,异常的出现是在所难免的,但是异常一旦出现,极有可能会直接导致程序崩溃,无法正常运行,所以异常一定要及时的做出对应的…...
CSS3常用的新功能总结
CSS3常用的新功能包括圆角、阴渐变、2D变换、3D旋转、动画、viewpor和媒体查询。 圆角、阴影 border-redius 对一个元素实现圆角效果,是通过border-redius完成的。属性为两种方式: 一个属性值,表示设置所有四个角的半径为相同值ÿ…...
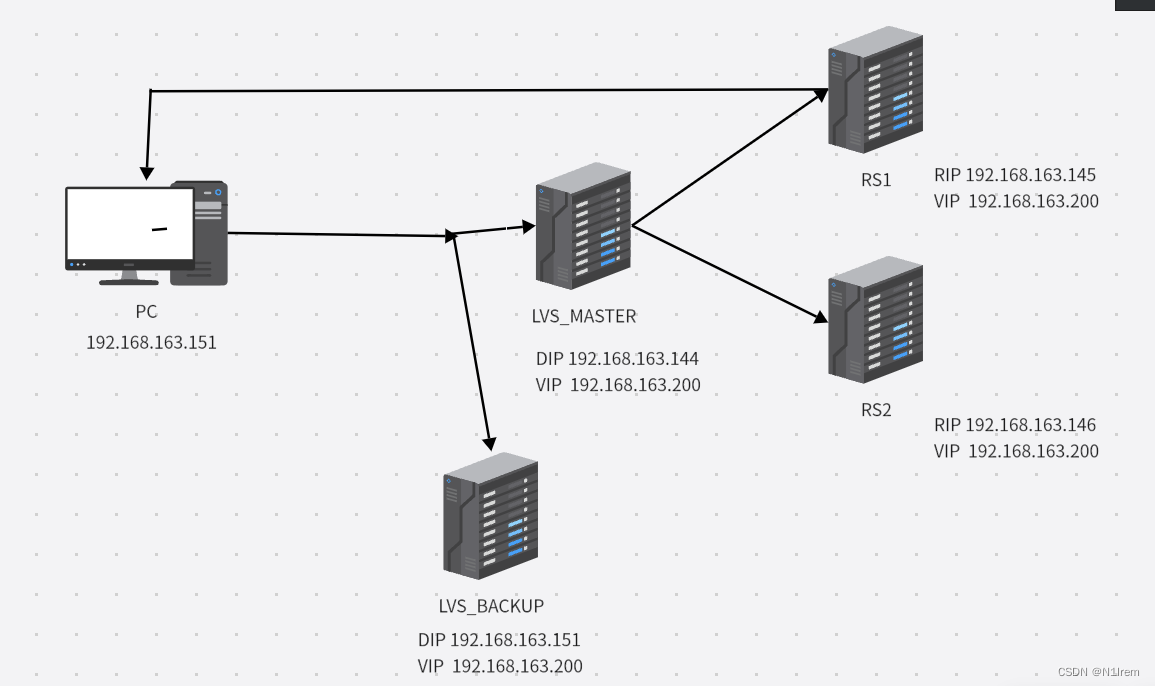
Lvs+KeepAlived高可用高性能负载均衡
目录 1.环境介绍 2.配置keepalived 3.测试 1.测试负载均衡 2.测试RS高可用 3.测试LVS高可用 3.1测试lvs主服务宕机 3.2.测试lvs主服务器恢复 4.我在实验中遇到的错误 1.环境介绍 环境:centos7 RS1---RIP1:192.168.163.145 VIP 192.168.163.200 RS2---RIP2…...

无涯教程-Android Online Test函数
Android在线测试模拟了真正的在线认证考试。您将看到基于 Android概念的多项选择题(MCQ),将为您提供四个options。您将为该问题选择最合适的答案,然后继续进行下一个问题,而不会浪费时间。完成完整的考试后,您将获得在线考试分数。 总问题数-20 最长时间-20分钟 Start Test …...

蓝桥杯打卡Day1
文章目录 全排列八皇后 一、全排列IO链接 本题思路:本题是一道经典的全排列问题,深度优先搜索即可解决。 #include <bits/stdc.h>constexpr int N10;std::string s; std::string ans; int n; bool st[N];void dfs(int u) {if(un){std::cout<<ans<…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
