快速排序学习
由于之前做有一题看到题解用了快排提升效率,就浅学了一下快速排序,还是似懂非懂。
首先快排的核心有两点,哨兵划分和递归。
- 哨兵划分:以数组中的某个数(一般为首位)为基准数,将数组划分为两个部分,小于基准数的都在左部分,大于基准数的都在右部分。(也就是说此时基准数的位置已经正确了)
- 递归:除了基准数已经处于正确位置,其他两部分还需要继续递归执行哨兵划分,当划分到子数组长度都为 1 了,那就没什么好划分的了,说明此时数组已经排序完了。
- 示例代码如下:
-
// 递归部分// l,r:子数组左右边界public void quickSort(int[] nums, int l, int r){// 说明数组长度被划分到此时为 1 了if(l>=r)return;// i 为基准数坐标,此时 i 左部分都小于 nums[i],右部分大于 nums[i]int i=partition(nums, l, r);// 对左右两部分递归执行哨兵划分quickSort(nums,l,i-1);quickSort(nums,i+1,r);}// 哨兵划分int partition(int[] nums, int l, int r) {int i=l, j=r;while(i<j){// 先从右边往前找比基准数小的,这个 i<j 的作用是:// 首先不会数组越界,其次它保证了不会出现错误的交换// 因为 i 左边的都是划分完的,j 右边的也都是划分完的,不应该再变动while(i < j && nums[j] >= nums[l]) j--;// 再从左边往后找比基准数大的while(i < j && nums[i] <= nums[l]) i++;// 然后把小的换到左边,大的换到右边swap(nums, i, j);}// 因为此时大致为// l i j// 中 小 小 大 大// 所以最后还需要把基准数移到正确的位置swap(nums, i, l);return i;}// 交换 nums[i] 和 nums[j]void swap(int[] nums, int i, int j) {int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;} - 时间复杂度的话不难看出,哨兵划分操作是 O(N),递归是递归 logN 轮,所以时间复杂度 O(logN) ,所以总共是 O(N logN)
- 最差情况下,每次哨兵划分都划分出 N-1 长度的数组以及长度 1 的数组,那时间复杂度就为 O(N2) 了
- 空间复杂度的话递归深度最好的情况平均情况下都是 logN,数组完全倒序让你排成正序那深度就为 N 了
算法优化
快排常见优化手段有「Tail Call」和「随机基准数」两种
Tail Call
上面也说了,因为是选取最左边的数为基准数,所以如果数组完全倒序,那么递归深度就会达到 N,也就是说最差空间复杂度为 O(N)
- 每轮递归时,仅对 较短的子数组 执行哨兵划分 partition() ,就可将最差的递归深度控制在 O(logN) (每轮递归的子数组长度都 ≤ 当前数组长度 / 2),即实现最差空间复杂度 O(logN) ,那么只需要修改 quickSort 部分即可
-
void quickSort(int[] nums, int l, int r) {// 子数组长度为 1 时终止递归while (l < r) {// 哨兵划分操作int i = partition(nums, l, r);// 仅递归至较短子数组,控制递归深度if (i - l < r - i) {quickSort(nums, l, i - 1);l = i + 1;} else {quickSort(nums, i + 1, r);r = i - 1;}}}
随机基准数:
由于每次都是取数组首位为基准数,所以当数组完全有序或完全倒序时,partition() 每次都是只划分了一个元素。也就是说当前情况下选择首位为基准数是最差的选择,但是我们仍然每次都坚定选择了最差的选择。
那么使用随机函数 ,每轮在子数组中随机选择一个元素作为基准数,就可以极大概率避免以上劣化情况。
值得注意的是,由于仍然可能出现最差情况(运气真的差到极点,每次都随机到首位,跟不随机一样),因此快速排序的最差时间复杂度仍为 O(N2) 。
代码仅需修改 partition() 方法,其余方法不变,在此省略。这个就很好理解了
-
int partition(int[] nums, int l, int r) {// 在闭区间 [l, r] 随机选取任意索引,并与 nums[l] 交换int ra = (int)(l + Math.random() * (r - l + 1));swap(nums, l, ra);// 以 nums[l] 作为基准数int i = l, j = r;while (i < j) {while (i < j && nums[j] >= nums[l]) j--;while (i < j && nums[i] <= nums[l]) i++;swap(nums, i, j);}swap(nums, i, l);return i;} - 参考原文
相关文章:

快速排序学习
由于之前做有一题看到题解用了快排提升效率,就浅学了一下快速排序,还是似懂非懂。 首先快排的核心有两点,哨兵划分和递归。 哨兵划分:以数组中的某个数(一般为首位)为基准数,将数组划分为两个部…...
【Vue3 知识第二讲】Vue3新特性、vue-devtools 调试工具、脚手架搭建
文章目录 一、Vue3 新特性1.1 重写双向数据绑定1.1.1 Vue2 基于Object.defineProperty() 实现1.1.2 Vue3 基于Proxy 实现 1.2 优化 虚拟DOM1.3 Fragments1.4 Tree shaking1.5 Composition API 二、 vue-devtools 调试工具三、环境配置四、脚手架目录介绍五、SFC 语法规范解析附…...

pytorch 基于masking对元素进行替换
描述 pytorch 基于masking对元素进行替换. 代码如下. 先展平再赋值. 代码 # map.shape [64,60,128] # infill.shape [64,17,128] # mask_indices.shape [64,60]map map.reshape(map.shape[0] * map.shape[1],map.shape[2]) [mask_indices.reshape(mask_indices.shape[0]*ma…...
Cyber RT学习笔记---7、Component组件认知与实践
7、Component组件认知与实践 前言 本文是对Cyber RT的学习记录,文章可能存在不严谨、不完善、有缺漏的部分,还请大家多多指出。 课程地址: https://apollo.baidu.com/community/course/outline/329?activeId10200 更多还请参考: [1] Apollo星火计划学习笔记——第…...

常见配置文件格式INI/XML/YAML/JSON/Properties/TOML/HCL/YAML Front Matter/.env介绍及实例
1. 常见配置文件INI XML YAML JSON Properties介绍 以下是常见配置文件格式(INI、XML、YAML、JSON、Properties、TOML、HCL、YAML Front Matter、.env)的比较: 配置文件格式简介语法定义优点缺点常见使用场景常见编程语言INI简单的文本文件…...

JS 方法实现复制粘贴
背景 以前我们一涉及到复制粘贴功能,实现思路一般都是: 创建一个 textarea 标签 让这个 textarea 不可见(定位) 给这个 textarea 赋值 把这个 textarea 塞到页面中 调用 textarea 的 select 方法 调用 document.execCommand…...

后端面试话术集锦第 十六 篇:java锁面试话术
这是后端面试集锦第十六篇博文——java锁面试话术❗❗❗ 1. 介绍一下乐观锁和悲观锁 乐观锁的话就是比较乐观,每次去拿数据的时候,认为别人不会修改,所以不会上锁,但是在更新的时候会判断一下在此期间别人有没有去更新这个数据,可以使用版本号机制或者CAS算法实现。 乐观…...
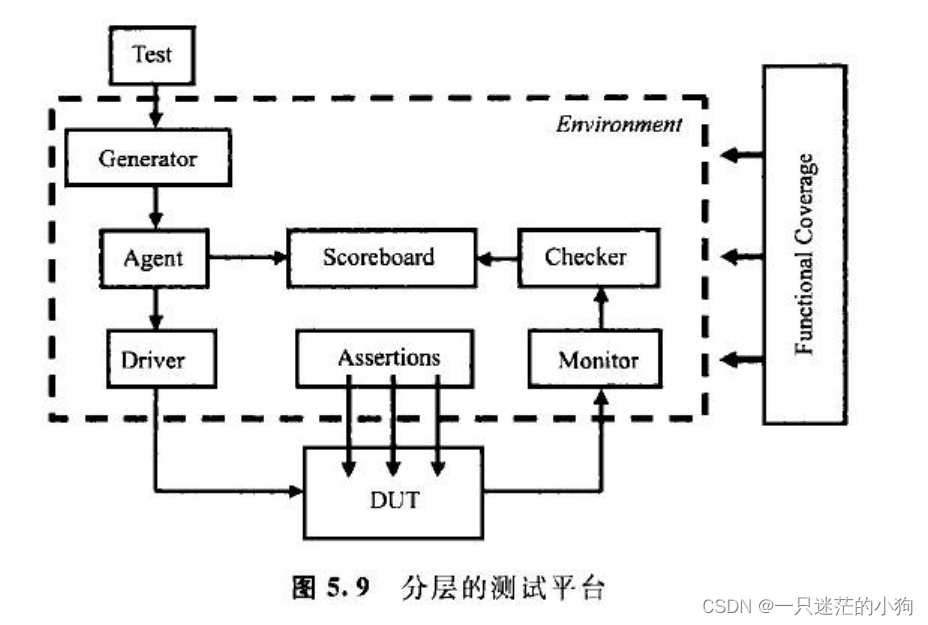
SystemVerilog 第5章 面向对象编程基础
5.1概述 对结构化编程语言,例如 Verilog和C语言来讲,它们的数据结构和使用这些数据结构的代码之间存在很大的沟壑。数据声明、数据类型与操作这些数据的算法经常放在不同的文件里,因此造成了对程序理解的困难。 Verilog程序员的境遇比C程序员更加棘手,因为Ⅴ erilog语言…...

指针进阶(1)
指针进阶 朋友们,好久不见,这次追秋给大家带来的是内容丰富精彩的指针知识的拓展内容,喜欢的朋友们三连走一波!!! 字符指针 在指针的类型中我们知道有一种指针类型为字符指针 char* ; 使用方法如…...
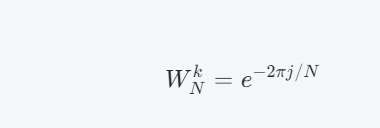
蝶形运算法
蝶形运算法是一种基于FFT(Fast Fourier Transform)算法的计算方法,其基本思想是将长度为N的DFT分解成若干个长度为N/2的DFT计算,并通过不断的合并操作得到最终的结果。该算法也称为“蝴蝶算法”,因为它的计算过程中需要…...
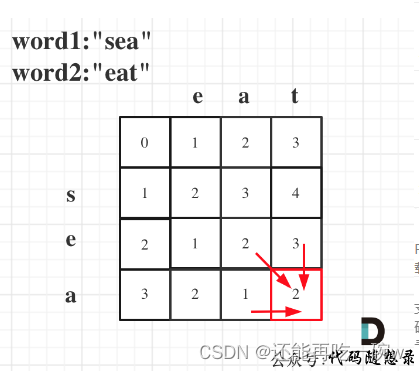
day 48|● 583. 两个字符串的删除操作 ● 72. 编辑距离
583. 两个字符串的删除操作 dp的含义:指0开头,i- 1和j - 1为结尾的两个序列的删除最小数 递推公式方面: 初始化方面:前面0行和0列的初值要赋好 func minDistance(word1 string, word2 string) int {dp : make([][]int, len(wor…...
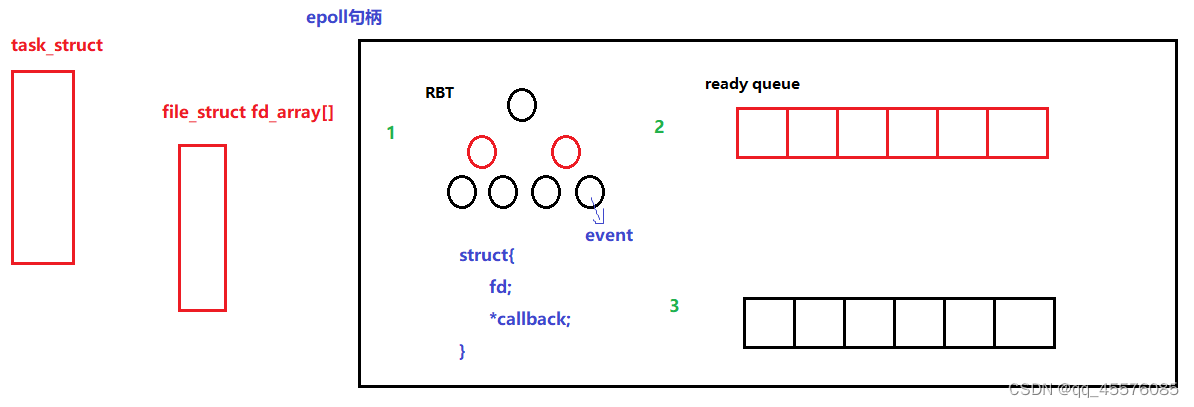
服务器(I/O)之多路转接
五种IO模型 1、阻塞等待:在内核将数据准备好之前,系统调用会一直等待。所有的套接字,默认都是阻塞方式。 2、非阻塞等待:如果内核没有将数据准备好,系统调用仍然会返回,并且会返回EWUOLDBLOCK或者EAGAIN错…...

后端面试话术集锦第 十三 篇:java集合面试话术
这是后端面试集锦第十三篇博文——java集合面试话术❗❗❗ 1. Java里常见的数据结构都有哪些以及特征 数组 数组是最常用的数据结构。 数组的特点是长度固定,可以用下标索引,并且所有的元素的类型都是一致的。 列表 列表和数组很相似,只不过它的大小可以改变。 列表一般都是…...
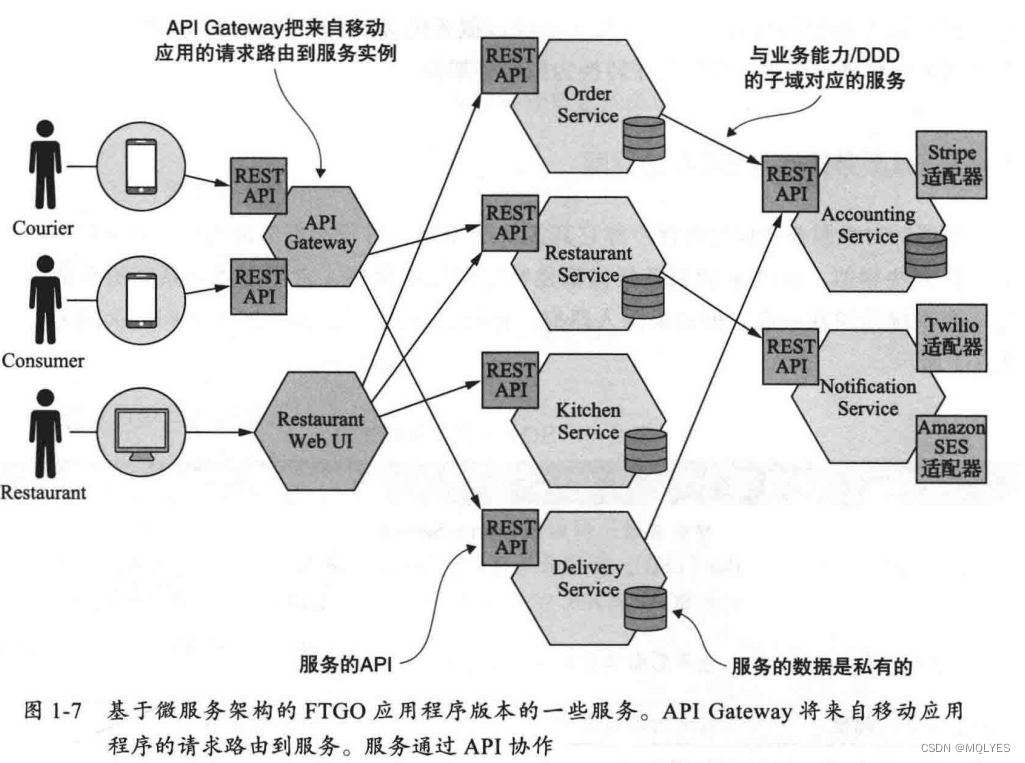
《微服务架构设计模式》第一章
逃离单体地狱 FTGO单体架构 作者用国外FTGO公司(一家做线餐饮外卖)的应用程序举例,阐述了单体架构的优缺点。FTGO应用架构如下: 应用程序是单体应用,具有六边形架构,最内侧是业务逻辑&…...

前端是如何打包的
前端项目的打包过程通常涉及将多个源文件(包括HTML、CSS、JavaScript等)合并、优化和压缩,以生成最终用于生产环境的静态资源。这个过程可以使用构建工具和打包工具来自动化完成。以下是前端项目的常见打包步骤: 1. **源代码编写…...

Qt 5.15编译(MinGW)及集成Crypto++ 8.7.0笔记
一、背景 为使用AES加密库(AES/CBC加解密),选用Crypto 库(官网)。 最新Crypto C库依次为:8.8.0版本(2023-6-25)、8.7.0(2022-8-7)和8.6.0(202…...
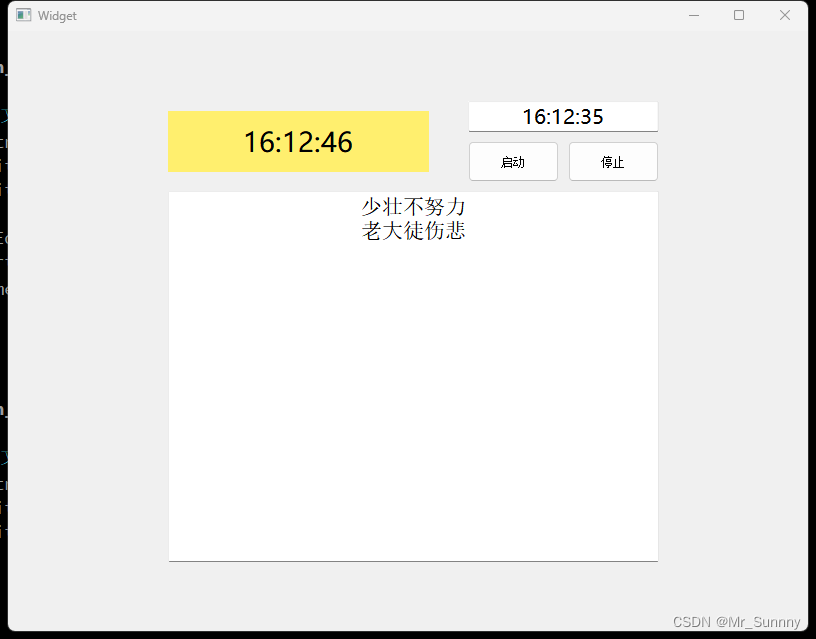
Qt 简单闹钟
//wiget.h#ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTime> //时间类 #include <QTimer> //定时器类 #include <QTextToSpeech> #include <QDebug> QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPA…...

简单谈下Spring、Spring MVC和Spring Boot
Spring是一个开源的轻量级框架,用于构建Java应用程序。它提供了一种全面的编程和配置模型,可以帮助开发人员构建各种类型的应用程序,从简单的控制台应用程序到大型企业级应用程序。Spring框架的主要目标是提高应用程序的可维护性、可扩展性和…...
利用python进行视频下载并界面播放快速下载素材
工具:python designer(python自带):UI界面设计工具 VLC:视频播放工具 需要的库如下: import os,platform os.environ[PYTHON_VLC_MODULE_PATH] "./vlc-3.0.14" import vlc from 脚本 import Player from …...
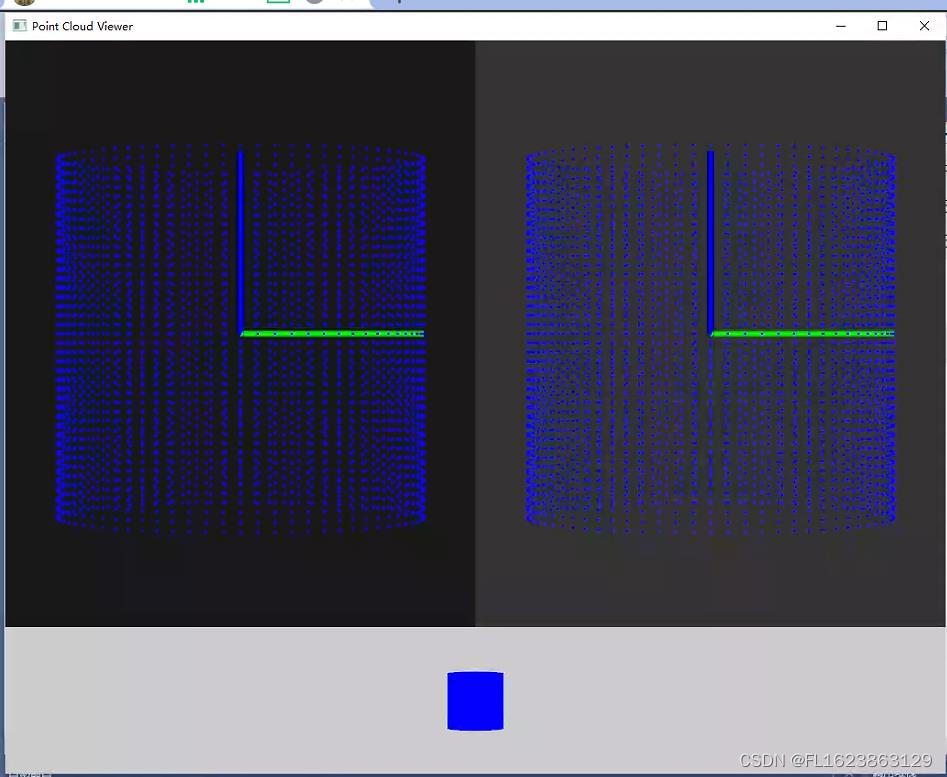
[C++][pcl]pcl安装后测试代码3
测试环境: vs2019 pcl1.12.1 代码: #include<iostream> #include <thread>#include <pcl/common/common_headers.h> #include <pcl/features/normal_3d.h> #include <pcl/io/pcd_io.h> #include <pcl/visualizatio…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
