当前位置： 首页 > news >正文

atcoder库中类欧（类欧几里得算法）floor_sum用法

news 2026/2/11 4:23:21

https://atcoder.jp/contests/practice2/tasks/practice2_c

求 ∑ i = 0 N − 1 f l o o r ( ( A × i + B ) / m ) \sum_{i = 0}^{N - 1} floor((A \times i + B) / m) ∑i=0N−1​floor((A×i+B)/m)

直接使用即可：

ans=floor_sum(n, m, A, B); //注意顺序

相关文章：

atcoder库中类欧（类欧几里得算法）floor_sum用法

https://atcoder.jp/contests/practice2/tasks/practice2_c 求 ∑ i 0 N − 1 f l o o r ( ( A i B ) / m ) \sum_{i 0}^{N - 1} floor((A \times i B) / m) ∑i0N−1​floor((AiB)/m) 直接使用即可： ansfloor_sum(n, m, A, B); //注意顺序...

编程日记 2023/9/6 14:18:40

后端面试话术集锦第 十一 篇：mybatis面试话术

这是后端面试集锦第十一篇博文——mybatis面试话术❗❗❗ 1. 介绍下mybatis，说说它的优缺点是什么？ Mybatis是一个半ORM（对象关系映射）的持久层框架，它内部封装了JDBC，开发时只需要关注SQL语句本身，不需要花费精力去处理加载驱动、创建连接、创建statement等繁杂的过程…...

编程日记 2023/9/6 14:17:39

SpringBoot运维实用篇、打包、运行、高级配置、多环境开发、日志

文章目录 SpringBoot运维实用篇YW-1.SpringBoot程序的打包与运行程序打包程序运行SpringBoot程序打包失败处理命令行启动常见问题及解决方案SpringBoot项目快速启动（Linux版） YW-2.配置高级YW-2-1.临时属性设置YW-2-2.配置文件分类YW-2-3.自定义配置文件…...

编程日记 2023/9/6 14:16:38

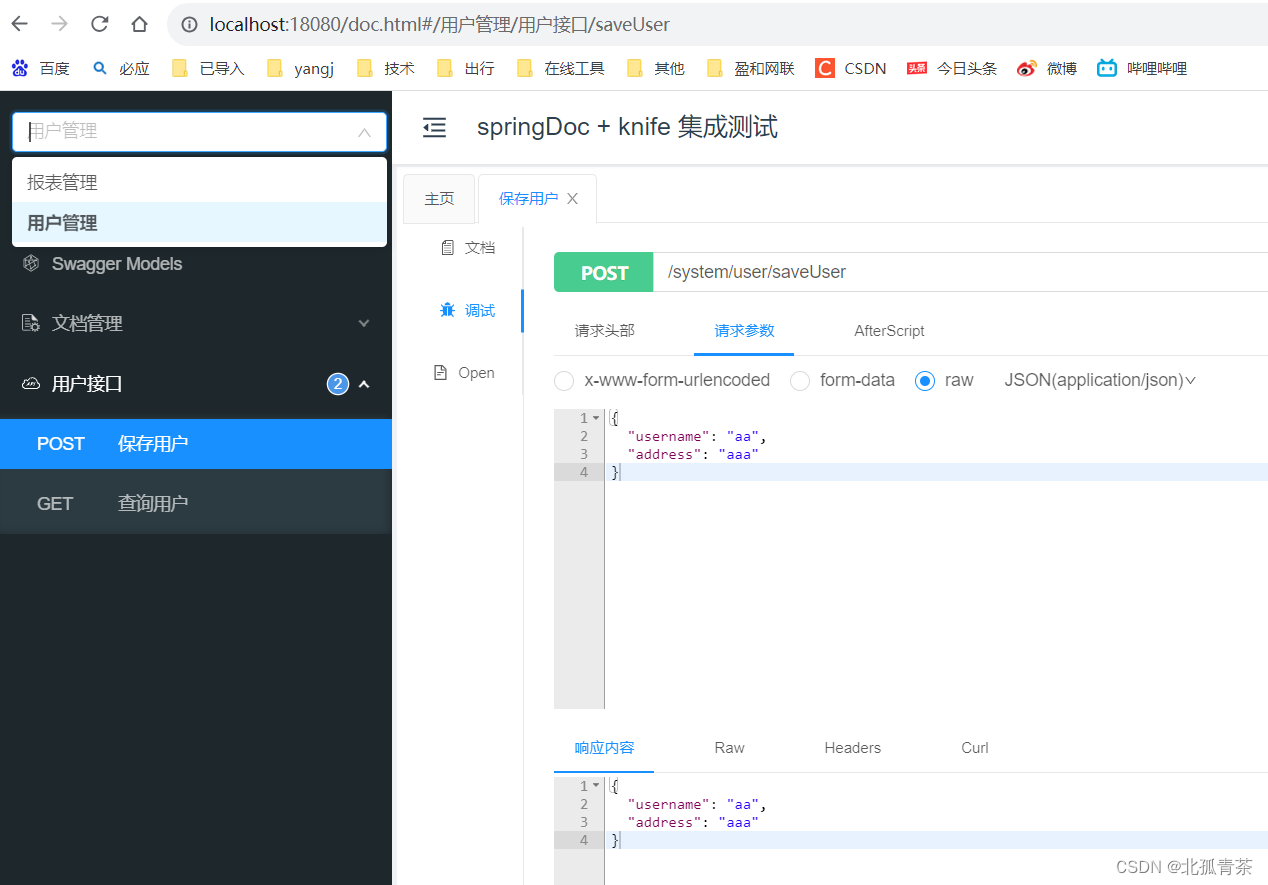
springdoc-openapi-ui 整合 knife，多模块分组，脚手架

pom文件&#xff1a; <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.o…...

编程日记 2023/9/6 14:15:36

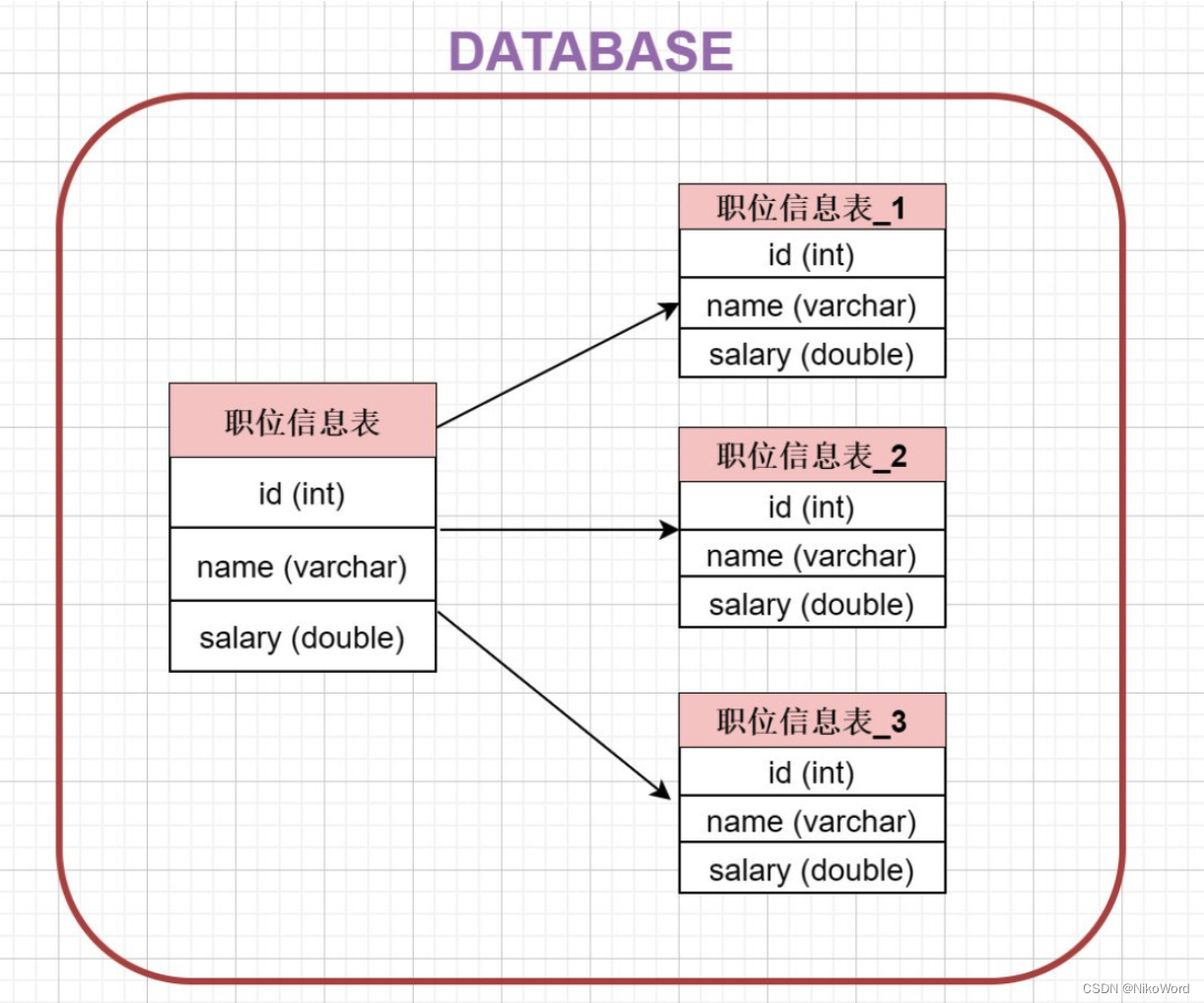
04-MySQL02

1、什么是索引下推&#xff1f; 索引下推&#xff08;index condition pushdown &#xff09;简称ICP&#xff0c;在Mysql5.6的版本上推出&#xff0c;用于优化查询。 需求: 查询users表中 "名字第一个字是张&#xff0c;年龄为10岁的所有记录"。 SELECT * FROM u…...

编程日记 2023/9/6 14:14:35

实现跨境电商测评和采退、LU卡、LU货最安全的系统方案

首先你要有一个稳定的测评环境系统&#xff0c;这个是做自养号退款、撸货、撸卡的基础。测评环境系统有很多&#xff0c;从早期的虚拟机&#xff0c;模拟机&#xff0c;云手机&#xff0c;VPS等等。这些系统方案先不说成本高&#xff0c;最重要的是成功率很低&#xff0c;所以一…...

编程日记 2023/9/6 14:13:32

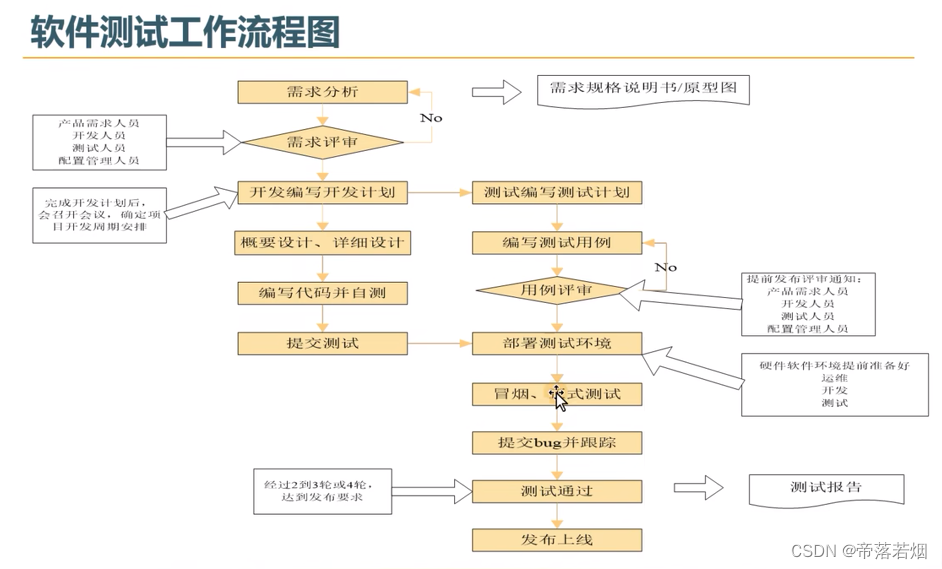
软件生命周期及流程

软件生命周期&#xff1a; 软件生命周期(SDLC&#xff0c;Systems Development Life Cycle)是软件开始研制到最终被废弃不用所经历的各个阶段. 需求分析阶段--输出需求规格说明书&#xff08;原型图&#xff09; 测试介入的晚--回溯成本高 敏捷开发模型&#xff1a; 从1990年…...

编程日记 2023/9/6 14:12:31

nginx使用详解

文章目录 一、前言二、nginx使用详解2.1、nginx特点2.2 静态文件处理2.3 反向代理2.4 负载均衡2.5 高级用法2.5.1 正则表达式匹配2.5.2 重定向 三、总结 一、前言 本文将详细介绍nginx的各个功能使用&#xff0c;主要包括 二、nginx使用详解 2.1、nginx特点 高性能&#xff…...

编程日记 2023/9/6 14:11:29

YOLOV7 添加 CBAM 注意力机制

用于学习记录 文章目录 前言一、CBAM1.1 models/common.py1.2 models/yolo.py1.3 yolov7/cfg/training/CBAM.yaml2.4 CBAM 训练结果图 前言 一、CBAM CBAM: Convolutional Block Attention Module 1.1 models/common.py class ChannelAttention(nn.Module):def __init__(sel…...

编程日记 2023/9/6 14:10:28

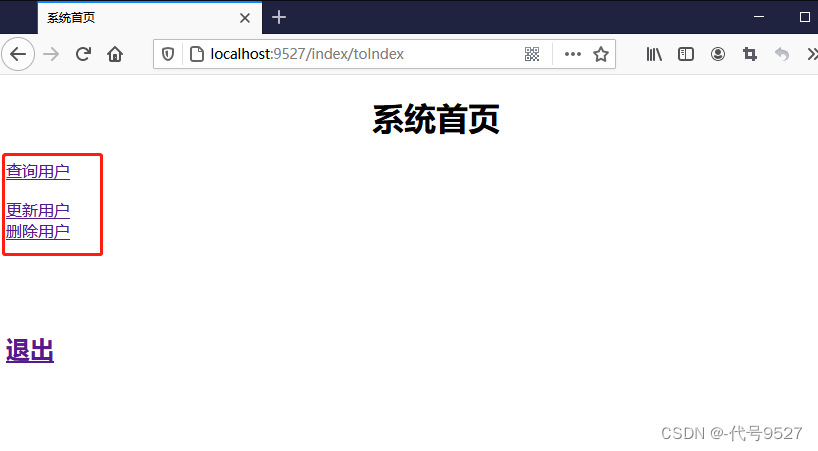
【SpringSecurity】七、SpringSecurity集成thymeleaf

文章目录 1、thymeleaf2、依赖部分3、定义Controller4、创建静态页面5、WebSecurityConfigurerAdapter6、权限相关7、当用户没有某权限时&#xff0c;页面不展示该按钮 1、thymeleaf 查了下读音&#xff0c;leaf/li:f/&#xff0c;叶子&#xff0c;前面的单词发音和时间time一…...

编程日记 2023/9/6 14:09:27

Go语言中的数组、切片和映射解析

目录 数组数组的声明数组循环 切片切片声明切片元素循环 映射Map的声明及初始化Map的遍历 数组 数组存放的是固定长度、相同类型的数据&#xff0c;而且这些存放的元素是连续的。 数组的声明 例如声明一个整形数组&#xff1a; array : [3]int{1, 2, 3}在类型名前加 [] 中括…...

编程日记 2023/9/6 14:08:25

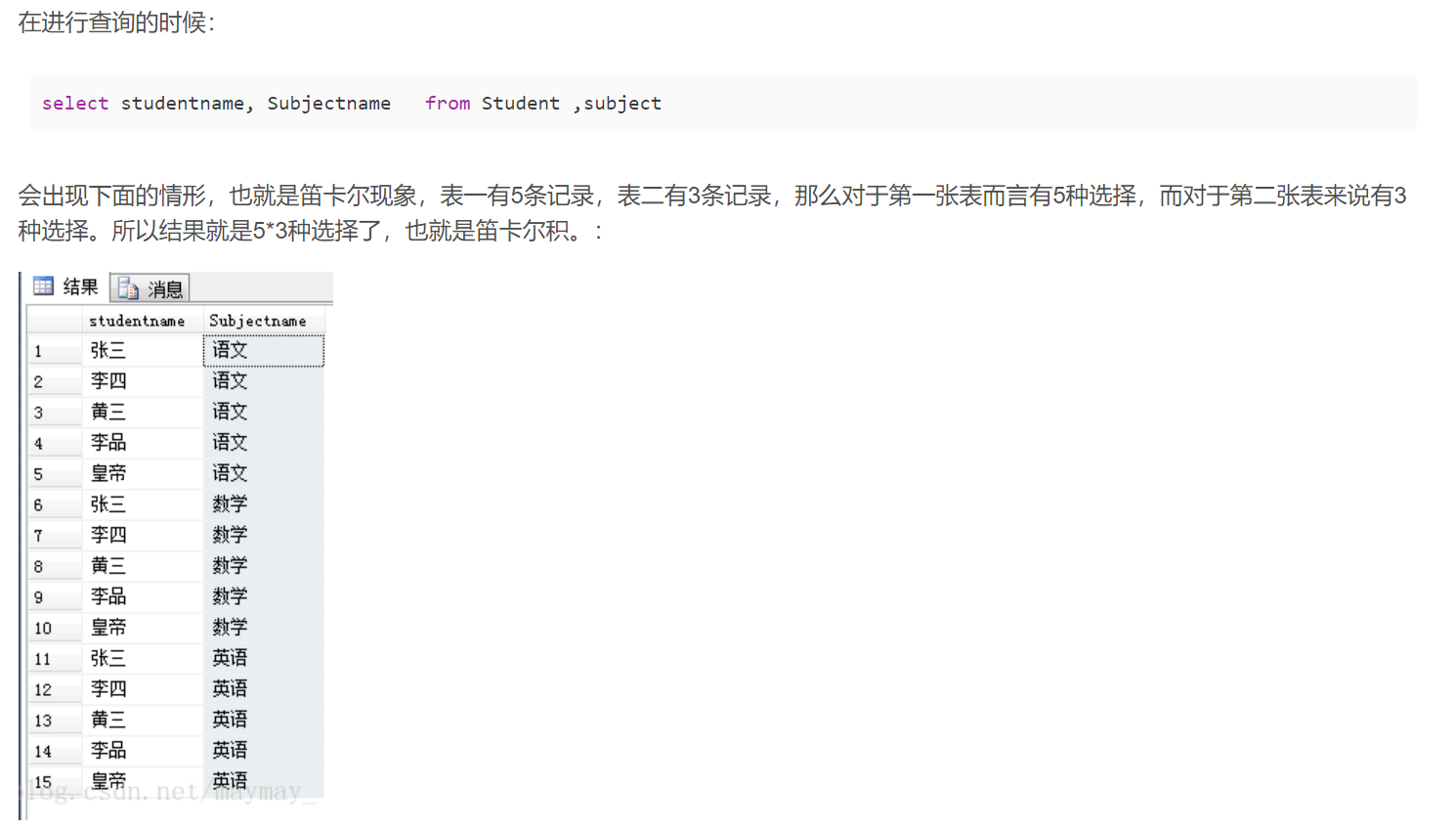
MySql学习笔记03——DQL（数据查询）基本命令

DQL 导入数据 首先使用use database进入数据库中&#xff0c;然后使用命令 source D:\mysql_learning\mysql_learning\document\bjpowernode.sql注意文件名不能有双引号&#xff0c;命令结尾没有分号。 SQL脚本 .sql文件是SQL脚本文件&#xff0c;它里面的内容都是SQL语句…...

编程日记 2023/9/6 14:07:24

操作系统的四大特性

一、并发性 指操作系统同时运行着多个程序&#xff0c;这些程序宏观上是同时运行的&#xff0c;但微观上其实是交替运行的 补充1&#xff1a;并发性区别于并行性 并发是指两个或多个事件在同一时间间隔内发生&#xff0c;事件宏观上是同时进行的&#xff0c;围观上市交替进行的…...

编程日记 2023/9/6 14:06:22

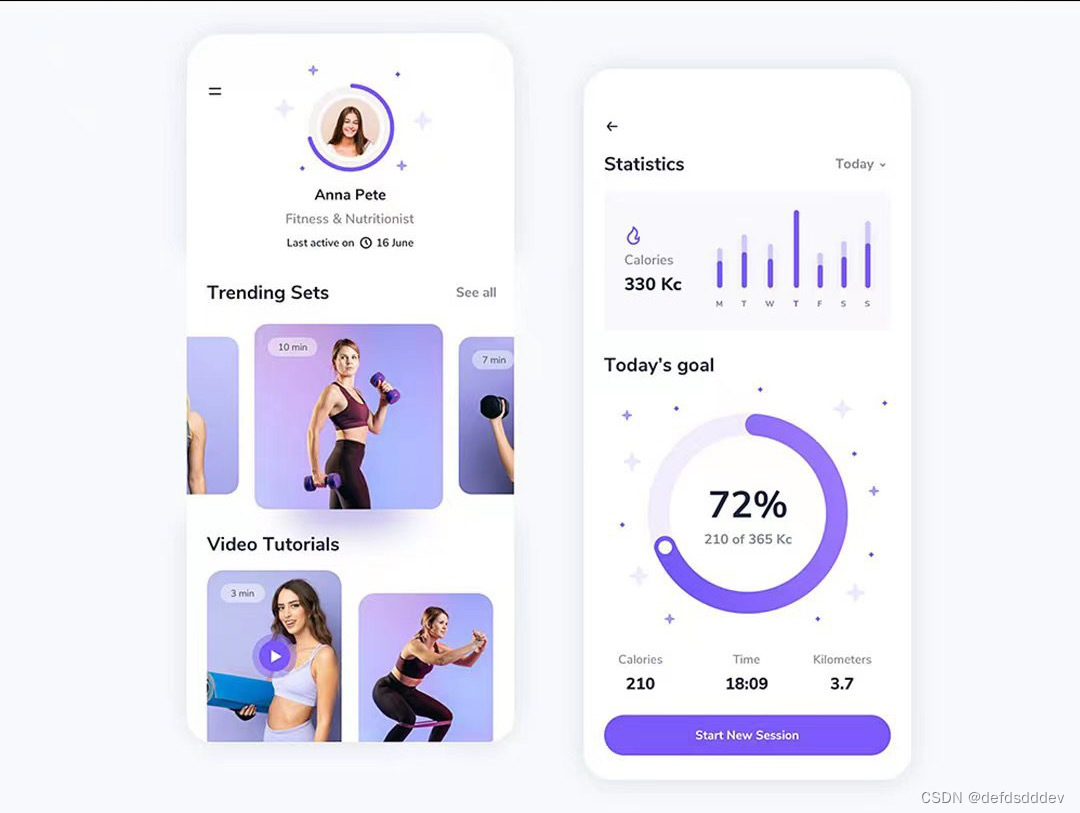
旅游攻略APP外包开发功能

旅游攻略APP是帮助旅行者计划和享受旅行的工具&#xff0c;下面列出了一些常见的旅游攻略APP功能&#xff0c;以及在上线这类应用时需要注意的问题&#xff0c;希望对大家有所帮助。北京木奇移动技术有限公司&#xff0c;专业的软件外包开发公司&#xff0c;欢迎交流合作。 常见…...

编程日记 2023/9/6 14:05:21

Apollo在Java中的使用

本节主要讲解在普通的 Java 项目和 Spring Boot 中如何使用 Apollo。 普通 Java 项目中使用 加入 Apollo Client 的 Maven 依赖&#xff0c;代码如下所示。 <dependency><groupId>com.ctrip.framework.apollo</groupId><artifactId>apollo-client<…...

编程日记 2023/9/6 14:04:18

Elasticsearch 全文搜索引擎 ---- IK分词器

原理&#xff1a;分词的原理&#xff1a;二叉树 首先讲一下为什么要出这个文章&#xff0c;前面我们讲过分词方法&#xff1a;中文分词搜索 pscws&#xff08;感兴趣的同学可以去爬楼看一下&#xff09;&#xff0c;那为什么要讲IK分词&#xff1f;最主要的原因是&…...

编程日记 2023/9/6 14:03:16

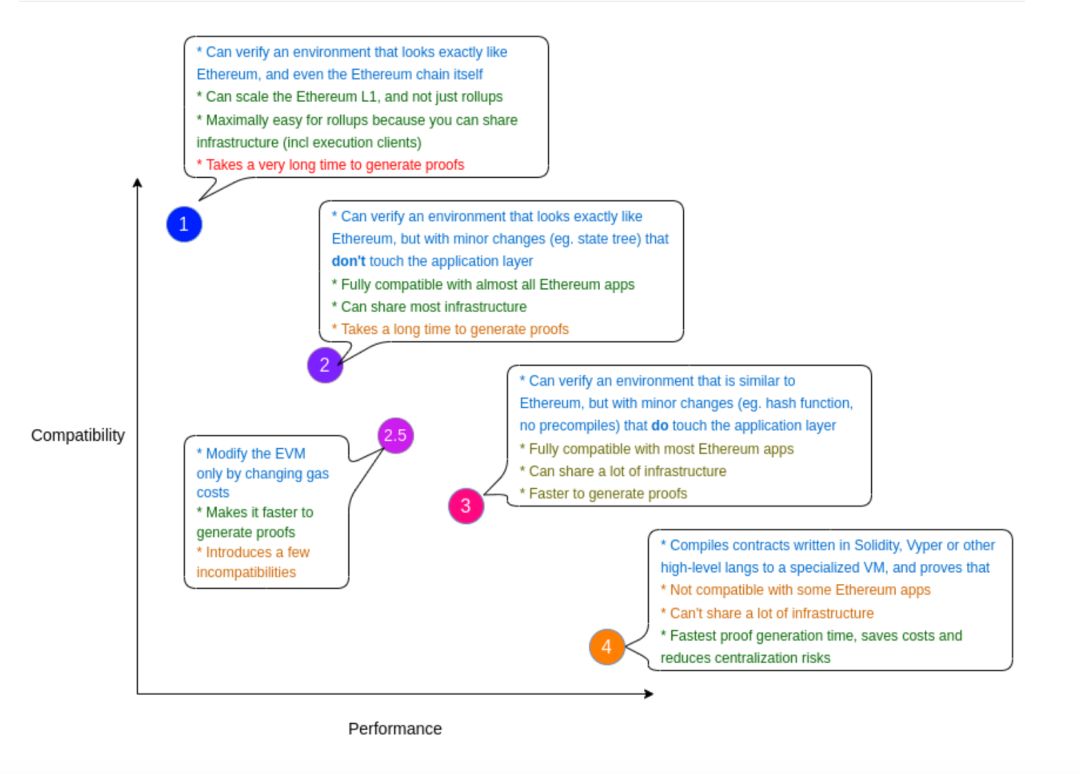
Layer 2盛夏已至，StarkNet如何实现价值跃迁？

作者&#xff5c;Jason Jiang Layer 2概念在2023年夏天迎来爆发。Coinbase、ConsenSys等加密巨头纷纷下场&#xff0c;其部署的原生L2解决方案Base、Linea在过去两个月内相继完成主网上线&#xff1b;被誉为L2 四大天王之一的StarkNet也在夏天顺利完成“量子跃迁”升级&#x…...

编程日记 2023/9/6 14:02:15

KaiwuDB 受邀亮相 2023 中国国际“软博会”

8月31日&#xff0c;第二十五届中国国际软件博览会&#xff08;以下简称“软博会”&#xff09;在天津盛大开幕。KaiwuDB 受邀亮相展会&#xff0c;围绕“塑造软件新生态&#xff0c;赋能发展新变革”主题&#xff0c;重点展示自研分布式多模数据库及各大行业解决方案&#xff…...

编程日记 2023/9/6 14:01:14

RS-485/RS-422收发器电路 DP3085 国产低成本替代MAX3085

DP3085是5V、半双工、15kV ESD 保护的 RS-485/RS-422 收发器电路&#xff0c;电路内部包含一路驱动器和一路接收器。 DP3085具有增强的摆率限制&#xff0c;助于降低输出 EMI 以及不匹配的终端连接引起的反射&#xff0c;实现 500kbps 的无误码数据传输。 DP3085芯片接收器输入…...

编程日记 2023/9/6 14:00:12

R-which函数（带有arr.ind参数）

目录 一、which()函数 二、元素位置 一、which()函数 which()函数是R语言中的一个基础函数&#xff0c;用于返回满足指定条件的元素的位置或索引。 语法&#xff1a;which(x, arr.ind FALSE, useNames TRUE) 参数&#xff1a; - x&#xff1a;一个向量、数组或矩阵&#x…...

编程日记 2023/9/6 13:59:11

应用升级/灾备测试时使用guarantee 闪回点迅速回退

1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间&#xff0c; 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点&#xff0c;不需要开启数据库闪回。…...

编程新知 2026/1/14 22:12:47

django filter 统计数量 按属性去重

在Django中&#xff0c;如果你想要根据某个属性对查询集进行去重并统计数量&#xff0c;你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求&#xff1a; 方法1&#xff1a;使用annotate()和Count 假设你有一个模型Item&#xff0c;并且你想…...

编程新知 2026/1/11 2:37:51

转转集团旗下首家二手多品类循环仓店“超级转转”开业

6月9日&#xff0c;国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解&#xff0c;“超级…...

编程新知 2026/2/8 4:08:40

C++ 求圆面积的程序（Program to find area of a circle）

给定半径r&#xff0c;求圆的面积。圆的面积应精确到小数点后5位。 例子&#xff1a; 输入&#xff1a;r 5 输出&#xff1a;78.53982 解释&#xff1a;由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982&#xff0c;因为我们只保留小数点后 5 位数字。 输…...

编程新知 2026/1/31 12:52:15

技术栈RabbitMq的介绍和使用

目录 1. 什么是消息队列&#xff1f;2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

编程新知 2026/2/10 6:20:58

JVM虚拟机：内存结构、垃圾回收、性能优化

1、JVM虚拟机的简介 Java 虚拟机（Java Virtual Machine 简称：JVM）是运行所有 Java 程序的抽象计算机，是 Java 语言的运行环境，实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息，使得 Java 程序只需生成在 JVM 上运行的目标代码（字节码），就可以…...

编程新知 2026/2/9 23:40:53

嵌入式学习笔记DAY33（网络编程——TCP）

一、网络架构 C/S &#xff08;client/server 客户端/服务器&#xff09;&#xff1a;由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序&#xff0c;负责提供用户界面和交互逻辑 &#xff0c;接收用户输入&#xff0c;向服务器发送请求&#xff0c;并展示服务…...

编程新知 2026/2/10 3:34:25

第八部分：阶段项目 6：构建 React 前端应用

现在&#xff0c;是时候将你学到的 React 基础知识付诸实践&#xff0c;构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段&#xff0c;你可以先使用模拟数据&#xff0c;或者如果你的后端 API&#xff08;阶段项目 5&#xff09;已经搭建好&#xff0c;可以直接连…...

编程新知 2025/9/21 1:58:01

python打卡第47天

昨天代码中注意力热图的部分顺移至今天 知识点回顾&#xff1a; 热力图 作业&#xff1a;对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图&#xff0c;展示模…...

编程新知 2025/12/11 8:10:41

Java中栈的多种实现类详解

Java中栈的多种实现类详解&#xff1a;Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...

编程新知 2025/12/3 1:36:31