数学建模--Topsis评价方法的Python实现
目录
1.算法流程简介
2.算法核心代码
3.算法效果展示
1.算法流程简介
"""
TOPSIS(综合评价方法):主要是根据根据各测评对象与理想目标的接近程度进行排序.
然后在现有研究对象中进行相对优劣评价。
其基本原理就是求解计算各评价对象与最优解和最劣解的距离来进行排序.
如果过评价对象最靠近最优解同时又最远离最劣解,则为最优;否则不是最优。
这样的评价方法需要多次统一标准,所以要求我们掌握正向化的求解方法.
"""2.算法核心代码
"""
Question1:现给予你20组有关水质特征的值,分别是含氧量 PH值 细菌总数 植物性营养物量四个参数,请你根据
Topsis方法将20条河流的水质进行对应的评价!
"""#Topsis综合评价法
import numpy as np
import matplotlib.pyplot as plt
"""
输入评价数据
20个评价数据包含了含氧量 PH值 细菌总数 植物性营养物量四个参数"""
data=np.array([[4.69, 6.59, 51, 11.94],[2.03, 7.86, 19, 6.46],[9.11, 6.31, 46, 8.91],[8.61, 7.05, 46, 26.43],[7.13, 6.5, 50, 23.57],[2.39, 6.77, 38, 24.62],[7.69, 6.79, 38, 6.01],[9.3, 6.81, 27, 31.57],[5.45, 7.62, 5, 18.46],[6.19, 7.27, 17, 7.51],[7.93, 7.53, 9, 6.52],[4.4, 7.28, 17, 25.3],[7.46, 8.24, 23, 14.42],[2.01, 5.55, 47, 26.31],[2.04, 6.4, 23, 17.91],[7.73, 6.14, 52, 15.72],[6.35, 7.58, 25, 29.46],[8.29, 8.41, 39, 12.02],[3.54, 7.27, 54, 3.16],[7.44, 6.26, 8, 28.41]])
#区分指标的性质并且进行正向化处理
"""
一般来说,数据指标分为4种形式:
1.极大值型:越大越好,比如利润
2.极小值型:越小越好,比如死亡数
3.中间值型:越趋近于某一个数越好,比如PH
4.区间值型:越趋近于某一个区间越好
##常见的转化公式
极大值型:x-x_min
极小值型:x_max-x
区间值型:在区间中为1,大于区间:1-(x-r)/M 小于区间:1-(l-x)/M
"""
# 定义position接收需要进行正向化处理的列
position = np.array([1, 2, 3])
# 定义处理类型:1 - > 极小型 2 - > 中间型 3 - > 区间型
Type = np.array([2, 1, 3])
# 定义正向化函数
def positivization(x:np.array,pos:int,type:int)->np.array:if type==1:#极小型值x=x.max()-xelif type==2:best=7#此处可以修改M=np.max(np.abs(x-best))x=1-np.abs(x-best)/Melse:#区间值型:在区间中为1,大于区间:1-(x-r)/M 小于区间:1-(l-x)/Ml=10#区间左端r=20#区间右端M0=max(l-x.min(),x.max()-r)x=np.where(x<l,1-(l-x)/M0,x)x=np.where(x>r,1-(x-r)/M0,x)x=np.where(x>l,1,x)return x
for i in range(len(position)):data[:, position[i]] = positivization(data[:, position[i]], position[i], Type[i])
#矩阵标准化求解
"""
已经正向化后,我们就能够进行矩阵的标准化求解了
把标准化的矩阵记作Z,对于每一个z(i,j)都有:
z(i,j)=x(i,j)/sqrt(sum(x(i,j)*x(i,j)))
"""
Z = data / np.sum(data * data, axis=0) ** 0.5
"""
计算得分并且归一化
"""
max_grd=np.max(Z)
min_grd=np.min(Z)
max_dist = np.sum((max_grd - Z) * (max_grd - Z), axis=1) ** 0.5
min_dist = np.sum((min_grd - Z) * (min_grd - Z), axis=1) ** 0.5
#最终得分
final_score = (min_dist / (max_dist + min_dist))
#归一化处理并且保留精度
final_score /= np.sum(final_score)
final_score = np.around(final_score, decimals=3)
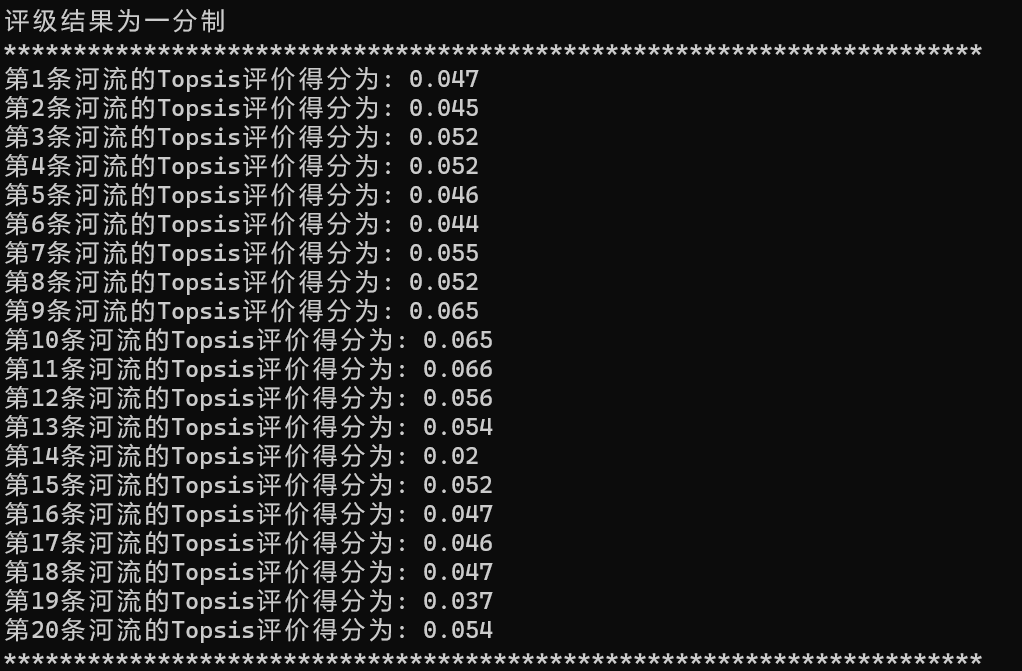
print("评级结果为一分制")
print("**********************************************************************")
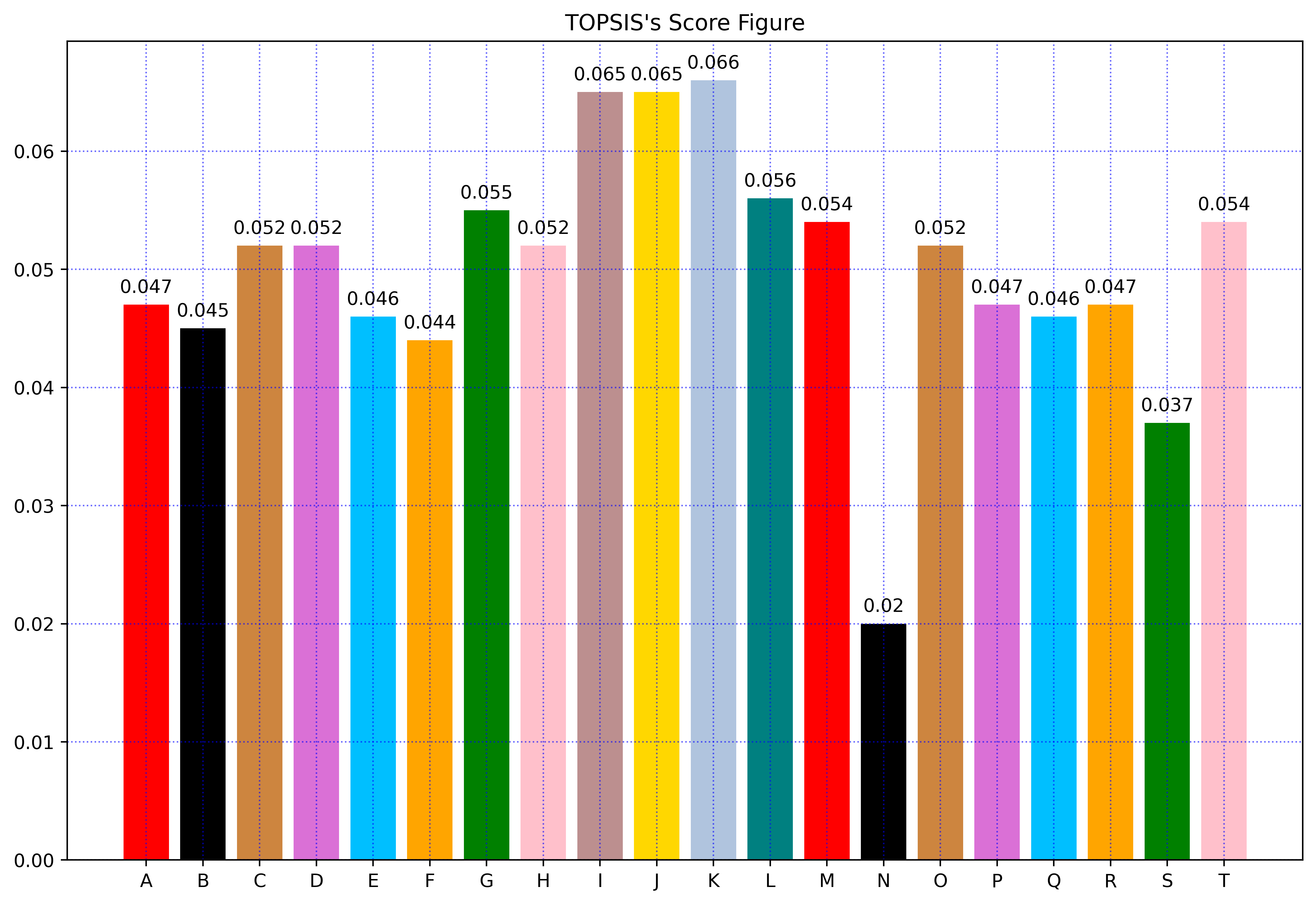
for i in range(len(final_score)):print("第{}条河流的Topsis评价得分为:".format(i+1),final_score[i])
print("**********************************************************************")
#绘制可视化图片
number=20#根据数据的个数进行修改即可
x = np.arange(number)
colors=['red','black','peru','orchid','deepskyblue', 'orange', 'green', 'pink', 'rosybrown', 'gold', 'lightsteelblue', 'teal']
x_label = [chr(i) for i in range(65,65+number)]#表示成A,B,C,......Z
#绘制可视化图
plt.figure(figsize=(12, 8))
plt.xticks(x, x_label)
#绘制条形统计图
plt.bar(x, final_score,color=colors)
#设置网格刻度
plt.grid(True,linestyle=':',color='b',alpha=0.6)
plt.title("TOPSIS's Score Figure")
#在柱状图上绘制数据
for xx, yy in zip(x, final_score):plt.text(xx, yy + 0.001, str(yy), ha='center')
plt.savefig('C:\\Users\\Zeng Zhong Yan\\Desktop\\TOPSIS Score Figure.png', dpi=500, bbox_inches='tight')
plt.show()
3.算法效果展示
相关文章:

数学建模--Topsis评价方法的Python实现
目录 1.算法流程简介 2.算法核心代码 3.算法效果展示 1.算法流程简介 """ TOPSIS(综合评价方法):主要是根据根据各测评对象与理想目标的接近程度进行排序. 然后在现有研究对象中进行相对优劣评价。 其基本原理就是求解计算各评价对象与最优解和最劣解的距离…...

超越时间与人力的软件开发智慧:《人月神话》
目录 1、写在前面2、沟通!沟通!沟通!3、“银弹论”4、“人月神话”不能成立的原因5、影响力6、图书推荐 1、写在前面 《人月神话》是由计算机科学家弗雷德里克布鲁克斯所著的一本经典著作,首次出版于1975年。这本书以一个个小故事…...

Java Stream 流对象(实用技巧)
目录 一、InputStream & OutputStream 1.1、InputStream 和 OutputStream 一般使用 1.2、特殊使用 1.2.1、如何表示文件读取完毕?(DataInputStream) 1.2.2、字符读取/文本数据读取(Scanner) 1.2.3、文件的随机…...

【用unity实现100个游戏之8】用Unity制作一个炸弹人游戏
文章目录 前言素材开始一、绘制地图二、玩家设置三、玩家移动四、玩家四方向动画运动切换 五、放置炸弹六、生成爆炸效果七、墙壁和可破坏障碍物的判断八、道具生成和效果九、玩家死亡十、简单的敌人AI十一、简单敌人AI十二、随机绘制地图十三、虚拟摇杆 最终效果待续源码完结 …...

简易版人脸识别qt opencv
1、配置文件.pro #------------------------------------------------- # # Project created by QtCreator 2023-09-05T19:00:36 # #-------------------------------------------------QT core guigreaterThan(QT_MAJOR_VERSION, 4): QT widgetsTARGET 01_face TEMP…...

如何系统地学习 JavaScript?
前言 在学习JavaScript前需要先将Html和Css的相关知识点弄清楚,Js的很多操作是要结合Html和Css,下面我总结了Html、Css和Js的相关学习知识点供参考,希望对你有所帮助喔~ Html 文档学习 【HTML 】w3school教程 :https://www.w3school.com.…...
)
对称二叉树(Leetcode 101)
题目 101. 对称二叉树 思路 使用层序遍历,遍历当前层的节点时,如该节点的左(右)孩子为空,在list中添加null,否则加入左(右)孩子的值。每遍历完一层则对当前list进行判断,…...
-3.5 图像分类数据集)
动手学深度学习(2)-3.5 图像分类数据集
文章目录 引言正文图像分类数据集主要包介绍主要流程具体代码练习 总结 引言 这里主要是看一下如何加载数据集,并且生成批次训练的数据。最大的收获是,知道了如何在训练阶段提高模型训练的性能 增加batch_size增加num_worker数据预加载 正文 图像分类…...

C标准输入与标准输出——stdin,stdout
🔗 《C语言趣味教程》👈 猛戳订阅!!! —— 热门专栏《维生素C语言》的重制版 —— 💭 写在前面:这是一套 C 语言趣味教学专栏,目前正在火热连载中,欢迎猛戳订阅&#…...
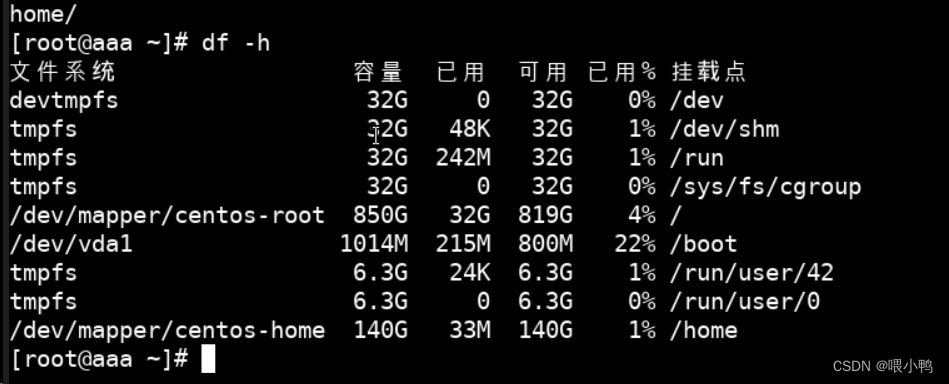
如何将home目录空间扩充到根目录下
目录 1、查看查看磁盘使用情况2、扩容思路3、卸载并删除/home4、扩大/root逻辑卷5、扩大/文件系统6、重建/home逻辑卷7、创建/home文件系统8、将新建的文件系统挂载到/home目录下9、恢复/home并删除备份10、再次查看看磁盘存储 系统:centos7.9 1、查看查看磁盘使用…...

Ceph PG Peering数据修复
ceph数据修复 当PG完成了Peering过程后,处于Active状态的PG就可以对外提供服务了。如果该PG的各个副本上有不一致的对象,就需要进行修复。 Ceph的修复过程有两种:Recovery和Backfill。 Recovery是仅依据PG日志中的缺失记录来修复不一致的对…...

服务器上使用screen和linux的基本操作
临时换源 pip install torch1.7.1 -i https://pypi.tuna.tsinghua.edu.cn/simple some-package pip install torch1.7.1 -i http://pypi.douban.com/simple some-package临时清华源和豆瓣源 配环境的一点小问题 我们尽量是去配置能满足代码的环境,而不要想着修改…...

Kafka3.0.0版本——文件存储机制
这里写木目录标题 一、Topic 数据的存储机制1.1、Topic 数据的存储机制的概述1.2、Topic 数据的存储机制的图解1.3、Topic 数据的存储机制的文件解释 二、Topic数据的存储位置示例 一、Topic 数据的存储机制 1.1、Topic 数据的存储机制的概述 Topic是逻辑上的概念,…...

Linux如何安装MySQL
Linux安装MySQL5.7 1、下载 官网下载地址:http://dev.mysql.com/downloads/mysql/ 2、复制下面几个文件 3、检查当前系统是否安装过mysql、检查当前mysql依赖环境、检查/tmp文件夹权限 1)检查当前系统是否安装过mysql,执行安装命令前&am…...

确保网络的安全技术介绍
防火墙技术 防火墙是隔离本地网络与外界网络的一道防御系统。通常用于内部局域网 与外部广域网之间,通过限制外部网络用户以非法手段来访问内部资源,来达到保 护内部网络的安全。根据安全规则,防火墙对任何外部网络访问内部网络的行为进 …...

机器学习练习
原文章添加链接描述...

算法通关村第十九关——最小路径和
LeetCode64. 给定一个包含非负整数的 m n 网格 grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 输入:grid[[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径1→3→1→1→1的总和最小。 public int minPath…...

Linux 访问进程地址空间函数 access_process_vm
文章目录 一、源码解析二、Linux内核 用途2.1 ptrace请求2.2 进程的命令行 参考资料 一、源码解析 /*** get_task_mm - acquire a reference to the tasks mm** Returns %NULL if the task has no mm. Checks PF_KTHREAD (meaning* this kernel workthread has transiently a…...

selenium 动态爬取页面使用教程以及使用案例
Selenium 介绍 概述 Selenium是一款功能强大的自动化Web浏览器交互工具。它可以模拟真实用户在网页上的操作,例如点击、滚动、输入等等。Selenium可以爬取其他库难以爬取的网站,特别是那些需要登录或使用JavaScript的网站。Selenium可以自动地从Web页面…...
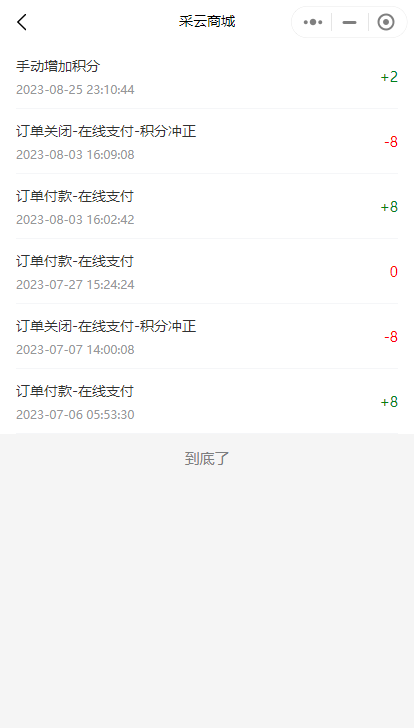
小程序中如何查看会员的积分和变更记录
积分是会员卡的一个重要功能,可以用于激励会员消费和提升用户粘性。在小程序中,商家可以方便地查看会员卡的积分和变更记录,以便更好地了解会员的消费行为和积分变动情况。下面将介绍如何在小程序中查看会员卡的积分和变更记录。 1. 找到指…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
