两种解法解决 LeetCode 27. 移除元素【C++】
移除元素
- 27. 移除元素
- 题目:[移除元素](https://leetcode.cn/problems/remove-element/description/)
- 示例和提示:
- 解法:
- 1. 暴力解法
- 2. 快慢指针
27. 移除元素
题目:移除元素
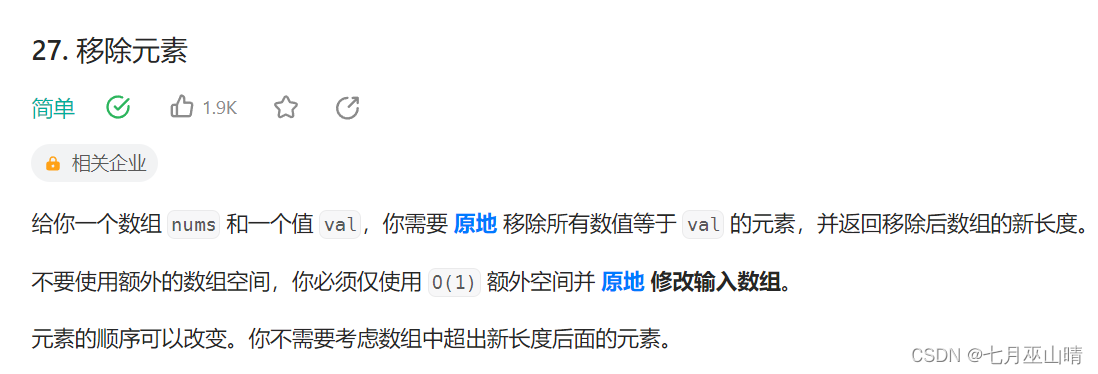
示例和提示:

解法:
1. 暴力解法
//暴力解法:
//实际上就是遍历数组找到需要删除的元素,然后再嵌套一层循环将该元素后面的依次向前覆盖。
class Solution {
public:int removeElement(vector<int>& nums, int val) {//为了不让每次循环都调用size()函数:int size = nums.size();//第一步,遍历目标数组:for(int i = 0; i < size; i++){//找到需要删除元素的位置;if(nums[i] == val){//删除元素从前向后遍历:for(int j = i+1; j < size; j++){nums[j-1] = nums[j];}//这里有一个迭代器失效问题,此时i指向原始数组中被删除元素的下一个位置,外层循环末尾//还会使得i++,没有判断就跳过了这个元素,所以得i--;i--;size--;}}return size;}
};
2. 快慢指针
//快慢指针法:
//很酷很丝滑的解法,快指针勇往无前的遍历,慢指针负责将快指针指向位置的元素复制到自己指向的位置,
//当快指针指向位置的元素需要删除时,慢指针停止赋值,直到快指针再次指向一个不需要删除的元素的位置。class Solution {
public:int removeElement(vector<int>& nums, int val) {int fastPoit = 0;int slowPoit = 0;int size = nums.size();for( ; fastPoit < size; fastPoit++){if(nums[fastPoit] != val){nums[slowPoit] = nums[fastPoit];slowPoit++;}}//slowPoit此时的指向正是新数组末尾的下一个位置,因为slowPoit++//是放在赋值最后执行的,所以刚好也就是新长度:return slowPoit;}
};
😄 创作不易,你的点赞和关注都是对我莫大的鼓励,再次感谢您的观看😄
相关文章:

两种解法解决 LeetCode 27. 移除元素【C++】
移除元素 27. 移除元素题目:[移除元素](https://leetcode.cn/problems/remove-element/description/)示例和提示:解法:1. 暴力解法 2. 快慢指针 27. 移除元素 题目:移除元素 示例和提示: 解法: 1. 暴力解…...
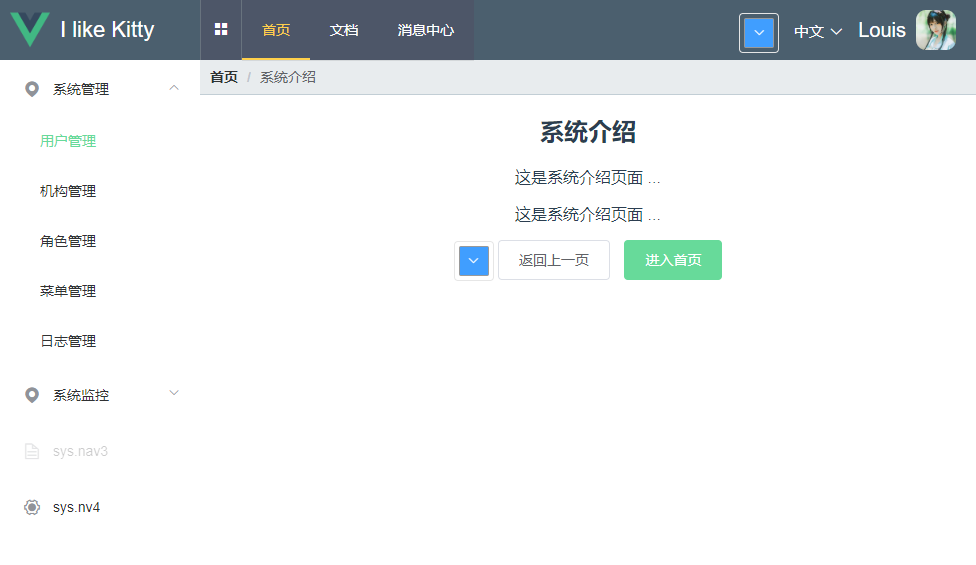
Vue + Element UI 前端篇(七):功能组件封装
组件封装 为了避免组件代码的臃肿,这里对主要的功能部件进行封装,保证代码的模块化和简洁度。 组件结构 组件封装重构后,试图组件结构如下图所示 代码一览 Home组件被简化,包含导航、头部和主内容三个组件。 Home.vue <te…...

QT QToolBox控件使用详解
本文详细的介绍了QToolBox控件的各种操作,例如:新建界面、添加页签、索引设置当前项、获取当前项的索引、获取当前项窗口、获取索引值是int的窗口、移除索引值项、获取项的数量、获取指定索引值、设置索引项是否激活、获取索引值项是否激活、设置项的图标…...
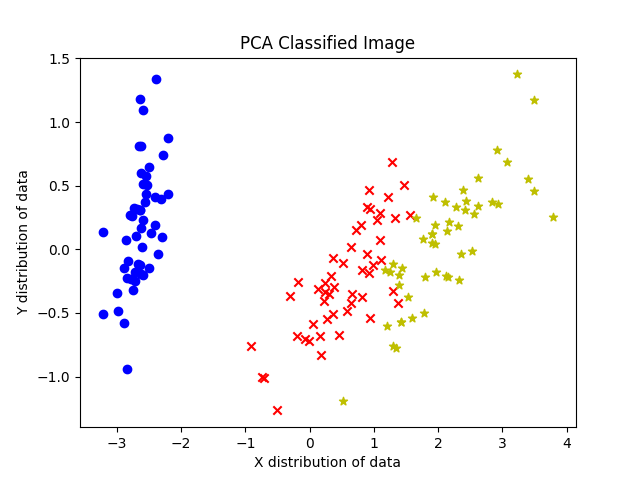
数学建模--主成分分析法(PCA)的Python实现(
目录 1.算法核心思想: 2.算法核心代码: 3.算法分类效果: 1.算法核心思想: 1.设置降维后主成分的数目为2 2.进行数据降维 3.设置main_factors1个划分类型 4.根据组分中的值进行分类 5.绘制出对应的图像 2.算法核心代码:…...

【数据结构篇】线性表2 —— 栈和队列
前言:上一篇我们介绍了顺序表和链表 (https://blog.csdn.net/iiiiiihuang/article/details/132615465?spm1001.2014.3001.5501), 这一篇我们将介绍栈和队列,栈和队列都是基于顺序表和链表来实现的 目录 栈ÿ…...

万物互联:软件与硬件的协同之道
在当今数字化时代,我们身边的一切似乎都与计算机和互联网有关。从智能手机到智能家居设备,从自动驾驶汽车到工业生产线,无论我们走到哪里,都能看到软件和硬件的协同作用。本文将探讨这种协同作用,解释软件和硬件如何相…...

ping: www.baidu.com: Name or service not known 写了DNS还是不行
环境描述:ESXI平台上,一台Centos7虚拟主机。 问题描述:平台上的其他的虚拟机可以正常ping通,就这台ping IP地址可以通,ping域名解析失败。 排查过程: 1、检查网卡配置文件和/etc/resolv.conf配置文件是否…...

C++中的decltype、std::declval 和 std::decay_t傻傻分不清楚
文章目录 前言它们是什么通俗解释总结 前言 在C中提到推导第一个映入脑海的可能是“模板”,当然有人也可能想到 auto,这些都是和推导相关的语言语法,再比如“完美转发”等等,总是就是他们的类型不用明明白白的写出来,…...

什么是Ubuntu LTS?与常规版本的区别
Ubuntu LTS(Long-Term Support)是Ubuntu操作系统的一个特殊版本,旨在提供更长时间的支持和稳定性。与常规的Ubuntu版本相比,LTS版本在以下几个方面有所不同: 支持周期更长: 使用Ubuntu LTS版本,…...

如何写一个可以找到工作的简历不至于太烂
简历是自己的一个很重要的标签,是获得面试的敲门砖,简历是要时常更新的,否则会错过一些机会。简历也是给自己的正反馈。 方法 ● 模仿,例如Boss,拉钩下面都给你一个案例模板供你参考,但是我觉得其实参考性…...

el-select 使用
案例: /* * label : 界面上展示的是哪个字段,我这里需要展示名称 * value : 绑定的字段,一般是id */<el-selectv-model"Form.BillNumber"placeholder"请选择"change"changeValue($event)"><el-optionv-for"…...

思维导图怎么变成ppt?4个思维导图一键生成ppt的方法
做好的思维导图如何变成一份ppt?本文罗列了4个可行方法,一起来看看吧。 一 直接复制粘贴 这是最简单的方法,虽然这样可能会花费一些时间,但可以确保内容排版和布局与你想要的一致。当然,我们大可使用更高效的方法。…...

3D点云处理:点云投影为2D图像 调平点云(附源码)
文章目录 0. 测试效果1. 基本内容1.1 计算点云位姿1.2 调平点云1.3 点云投影2. 代码实现文章目录:3D视觉个人学习目录微信:dhlddxB站: Non-Stop_0. 测试效果...

mysql 查询优化 、索引失效
查询优化 物理查询优化 通过索引和表连接方式等技术来进行优化,这里重点需要掌握索引的使用 逻辑查询优化 通过SQL 等价变换 提升查询效率,直白一点就是说,换一种查询写法执行效率可能更高 索引失效 计算、函数、类型转换(自动或…...
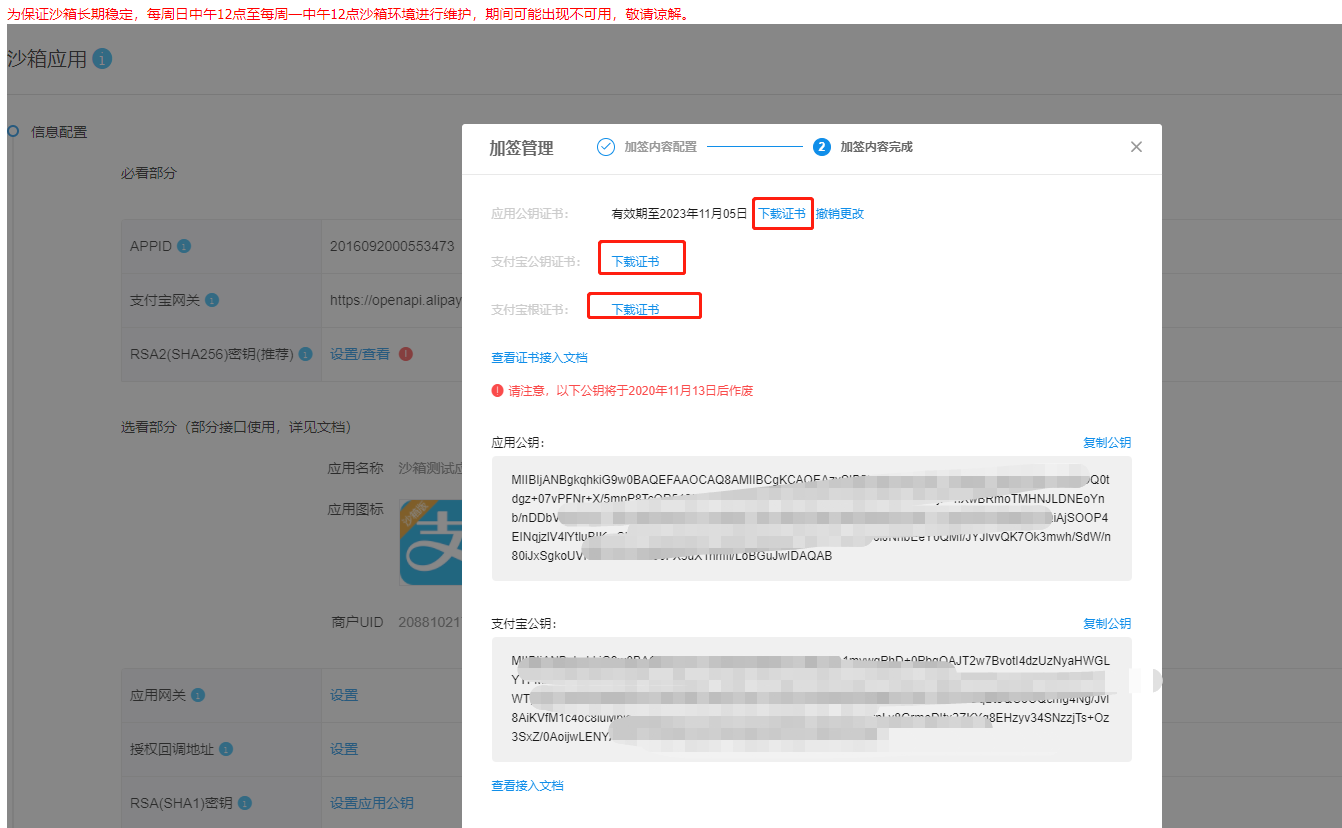
支付宝pc支付(springboot版),简单配置即可实现支付
概述 支付宝pc支付,只需要修改配置就可以实现支付,0基础小白都可以用。使用springboot编写,简单易用。 详细 DEMO简介 springboot整合支付宝pc支付,仅仅需要少量的配置,就可以实现pc支付。 项目截图 支付流程 用户…...
【Redis专题】Redis持久化、主从与哨兵架构详解
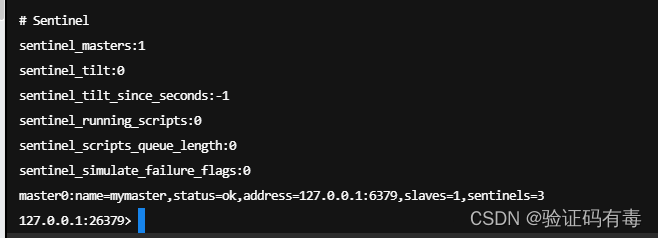
目录 前言课程目录一、Redis持久化1.1 RDB快照(Snapshot):二进制文件基本介绍开启/关闭方式触发方式bgsave的写时复制(COW,Copy On Write)机制优缺点 1.2 AOF(append-only file)&…...

【vue2第十三章】自定义指令 自定义v-loading指令
自定义指令 像 v-html,v-if,v-for都是vue内置指令,而我们也可以封装自定义指令,提升编码效率。 什么是自定义指令? 自己定义的一些指令,可以进行一些dom操作,扩展格外的功能。比如让图片懒加载…...
(插值查找))
数据结构--6.3查找算法(静态、动态)(插值查找)
静态查找:数据集合稳定,不需要添加,删除元素的查找操作。 动态查找:数据集合在查找的过程中需要同时添加或删除元素的查找操作。 对于静态查找来说,我们不妨可以用线性表结构组织数据,这样可以使用顺序查找…...
Spring Boot日志基础使用 设置日志级别
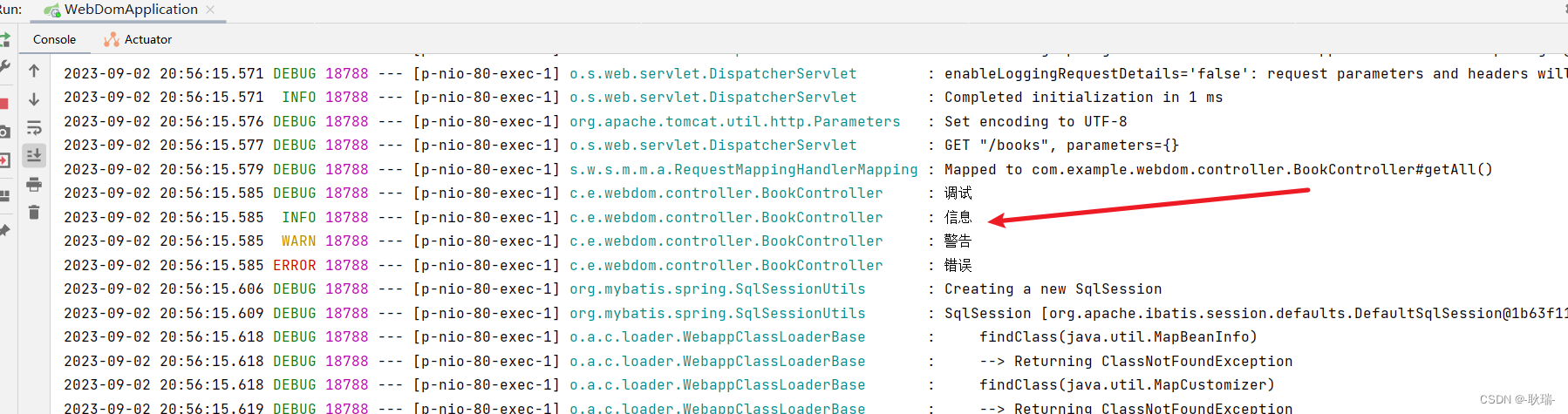
然后 我们来说日志 日志在实际开发中还是非常重要的 即可记录项目状态和一些特殊情况发生 因为 我们这里不是将项目 所以 讲的也不会特别深 基本还是将Spring Boot的日志设置或控制这一类的东西 相对业务的领域我们就不涉及了 日志 log 初期最明显的作用在于 开发中 你可以用…...
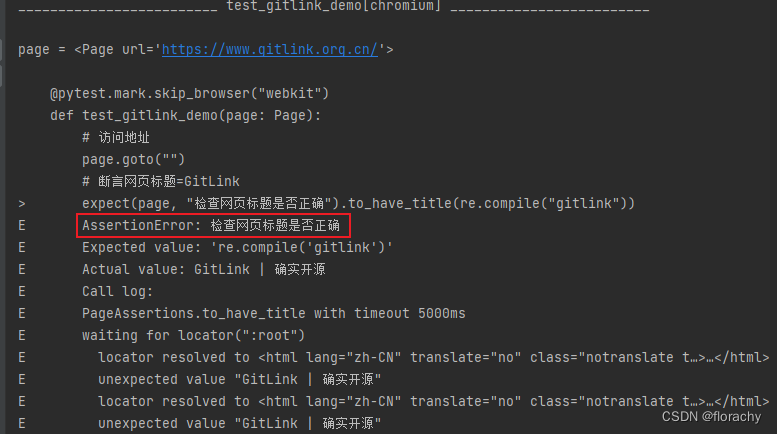
Playwright for Python:断言
一、支持的断言 Playwright支持以下几种断言: 断言描述expect(locator).to_be_checked()复选框被选中expect(locator).to_be_disabled()元素是禁用状态expect(locator).to_be_editable()元素是可编辑状态expect(locator).to_be_empty()容器是空的expect(locator).…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
