c++中的对齐问题
c++中的对齐问题
需要对齐的原因
尽管内存是以字节为单位,但是大部分处理器并不是按字节块来存取内存的.它一般会以双字节,四字节,8字节,16字节甚至32字节为单位来存取内存,我们将上述这些存取单位称为内存存取粒度.
现在考虑4字节存取粒度的处理器取int类型变量(32位系统),该处理器只能从地址为4的倍数的内存开始读取数据。
假如没有内存对齐机制,数据可以任意存放,现在一个int变量存放在从地址1开始的联系四个字节地址中,该处理器去取数据时,要先从0地址开始读取第一个4字节块,剔除不想要的字节(0地址),然后从地址4开始读取下一个4字节块,同样剔除不要的数据(5,6,7地址),最后留下的两块数据合并放入寄存器.这需要做很多工作.

对齐的规则
有效对齐值:是 #pragma pack(n)和结构体中最长数据类型长度中较小的那个。有效对齐值也叫对齐单位。
注意:
#pragma pack(n)中的n可以取(1 , 2 , 4 , 8 , 16)中的任意一值。
2)规则:
-
结构体变量的首地址是有效对齐值(对齐单位)的整数倍。
-
结构体第一个成员的偏移量(offset)为0,以后每个成员相对于结构体首地址的 offset 都是该成员大小与有效对齐值中较小那个的整数倍,如有需要编译器会在成员之间加上填充字节。
-
结构体的总大小为有效对齐值的整数倍,如有需要编译器会在最末一个成员之后加上填充字节。
-
结构体内类型相同的连续元素将在连续的空间内,和数组一样。
运用上面的规则,下面通过实际的例子进行计算。
例1:
#include <iostream>struct MyStruct {char c;int i;short s;
};int main()
{MyStruct obj;std::cout << "start addr of obj = " << (void*)&obj << std::endl;std::cout << "offset of c = " << offsetof(MyStruct,c) << std::endl;std::cout << "offset of i = " << offsetof(MyStruct,i) << std::endl;std::cout << "offset of s = " << offsetof(MyStruct,s) << std::endl;std::cout << "sizeof MyStruct = " << sizeof(MyStruct);
}
执行结果如下:
start of obj = 0x7fff2e8d1e94
offset of c = 0
offset of i = 4
offset of s = 8
sizeof MyStruct = 12
结构中最长的数据类型是int,长度也为4。因此结构体的有效对齐值是4。
对于c变量而言,没有悬念,将排在0偏移地址处。
对于变量i,类型为int,长度为4,int和有效对齐值的最小值为4,因此i需要排布在4的整数倍上,因此第一个符合要求的偏移量就是4。
对于变量s,类型为short,长度为2,short和有效对齐值二者中的最小值为2,第一个符合要求的地址为8。
到目前为止,使用的空间大小是10,而结构体大小需要满足有效对齐值的整数倍,因此需要2个填充,因此结构体最终大小是12。

例2:
#include <iostream>
#pragma pack(2)
struct MyStruct {char c;int i;short s;
};int main()
{MyStruct obj;std::cout << "start addr of obj = " << (void*)&obj << std::endl;std::cout << "offset of c = " << offsetof(MyStruct,c) << std::endl;std::cout << "offset of i = " << offsetof(MyStruct,i) << std::endl;std::cout << "offset of s = " << offsetof(MyStruct,s) << std::endl;std::cout << "sizeof MyStruct = " << sizeof(MyStruct);
}
执行结果如下:
start addr of obj = 0x7fff488e3418
offset of c = 0
offset of i = 2
offset of s = 6
sizeof MyStruct = 8
首先#pragma pack设置的对齐值是2,结构中最长的数据类型是int,长度也为4。因此结构体的有效对齐值是2。
对于c变量而言,没有悬念,将排在0偏移地址处。
对于变量i,类型为int,长度为4,int和有效对齐值的最小值为2,因此i需要排布在2的整数倍上,因此第一个符合要求的偏移量就是2。
对于变量s,类型为short,长度为2,short和有效对齐值二者中的最小值为2,第一个符合要求的地址为6。
到目前为止,使用的空间大小是8,已经满足结构体大小是有效对齐值的整数倍的要求。

#include <iostream>
#pragma pack(1)
struct MyStruct {char c;int i;short s;
};int main()
{MyStruct obj;std::cout << "start addr of obj = " << (void*)&obj << std::endl;std::cout << "offset of c = " << offsetof(MyStruct,c) << std::endl;std::cout << "offset of i = " << offsetof(MyStruct,i) << std::endl;std::cout << "offset of s = " << offsetof(MyStruct,s) << std::endl;std::cout << "sizeof MyStruct = " << sizeof(MyStruct);
}
执行结果如下:
start addr of obj = 0x7ffe96c067a9
offset of c = 0
offset of i = 1
offset of s = 5
sizeof MyStruct = 7
首先#pragma pack设置的对齐值是1,结构中最长的数据类型是int,长度也为4。因此结构体的有效对齐值是1。
对于c变量而言,没有悬念,将排在0偏移地址处。
对于变量i,类型为int,长度为4,int和有效对齐值的最小值为,因此i需要排布在2的整数倍上,因此第一个符合要求的偏移量就是1。
对于变量s,类型为short,长度为2,short和有效对齐值二者中的最小值为2,第一个符合要求的地址为5。
到目前为止,使用的空间大小是7,已经满足结构体大小是有效对齐值的整数倍的要求。

例4:
#include <iostream>
#include <emmintrin.h>struct MyStruct {char c;__m128i i;
};int main()
{MyStruct obj;std::cout << "start addr of obj = " << (void*)&obj << std::endl;std::cout << "offset of c = " << offsetof(MyStruct,c) << std::endl;std::cout << "offset of i = " << offsetof(MyStruct,i) << std::endl;std::cout << "sizeof MyStruct = " << sizeof(MyStruct);
}
执行结果如下:
start addr of obj = 0x7fff9d47cd90
offset of c = 0
offset of i = 16
sizeof MyStruct = 32
首先,结构中最长的数据类型是__m128i,长度为16。因此结构体的有效对齐值是16。
对于c变量而言,没有悬念,将排在0偏移地址处。
对于变量i,类型为__m128i,长度为16,__m128i和有效对齐值的最小值为16,因此i需要排布在2的整数倍上,因此第一个符合要求的偏移量就是16。

例5:
#include <iostream>
#include <emmintrin.h>#pragma pack(8)
struct MyStruct {char c;__m128i i;
};int main()
{MyStruct obj;std::cout << "start addr of obj = " << (void*)&obj << std::endl;std::cout << "offset of c = " << offsetof(MyStruct,c) << std::endl;std::cout << "offset of i = " << offsetof(MyStruct,i) << std::endl;std::cout << "sizeof MyStruct = " << sizeof(MyStruct);
}
执行结果如下:
start addr of obj = 0x7ffddbec2c40
offset of c = 0
offset of i = 8
sizeof MyStruct = 24
首先#pragma pack设置的对齐值是8,结构中最长的数据类型是__m128i,长度为16。因此结构体的有效对齐值是8。
对于c变量而言,没有悬念,将排在0偏移地址处。
对于变量i,类型为__m128i,长度为16,__m128i和有效对齐值的最小值为8,因此i需要排布在2的整数倍上,因此第一个符合要求的偏移量就是8。

总结
- 为了高效的访问内存数据,通常需要对内存数据进行对齐。
#pragma pack(n)用于设置的对齐有效值,如果设置比结构体的最长成员还大的对齐值将是无效的。
相关文章:

c++中的对齐问题
c中的对齐问题 需要对齐的原因 尽管内存是以字节为单位,但是大部分处理器并不是按字节块来存取内存的.它一般会以双字节,四字节,8字节,16字节甚至32字节为单位来存取内存,我们将上述这些存取单位称为内存存取粒度. 现在考虑4字节存取粒度的处理器取in…...
算法_C++—— 存在重复元素)
力扣(LeetCode)算法_C++—— 存在重复元素
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。 示例 1: 输入:nums [1,2,3,1] 输出:true 示例 2: 输入:nums …...
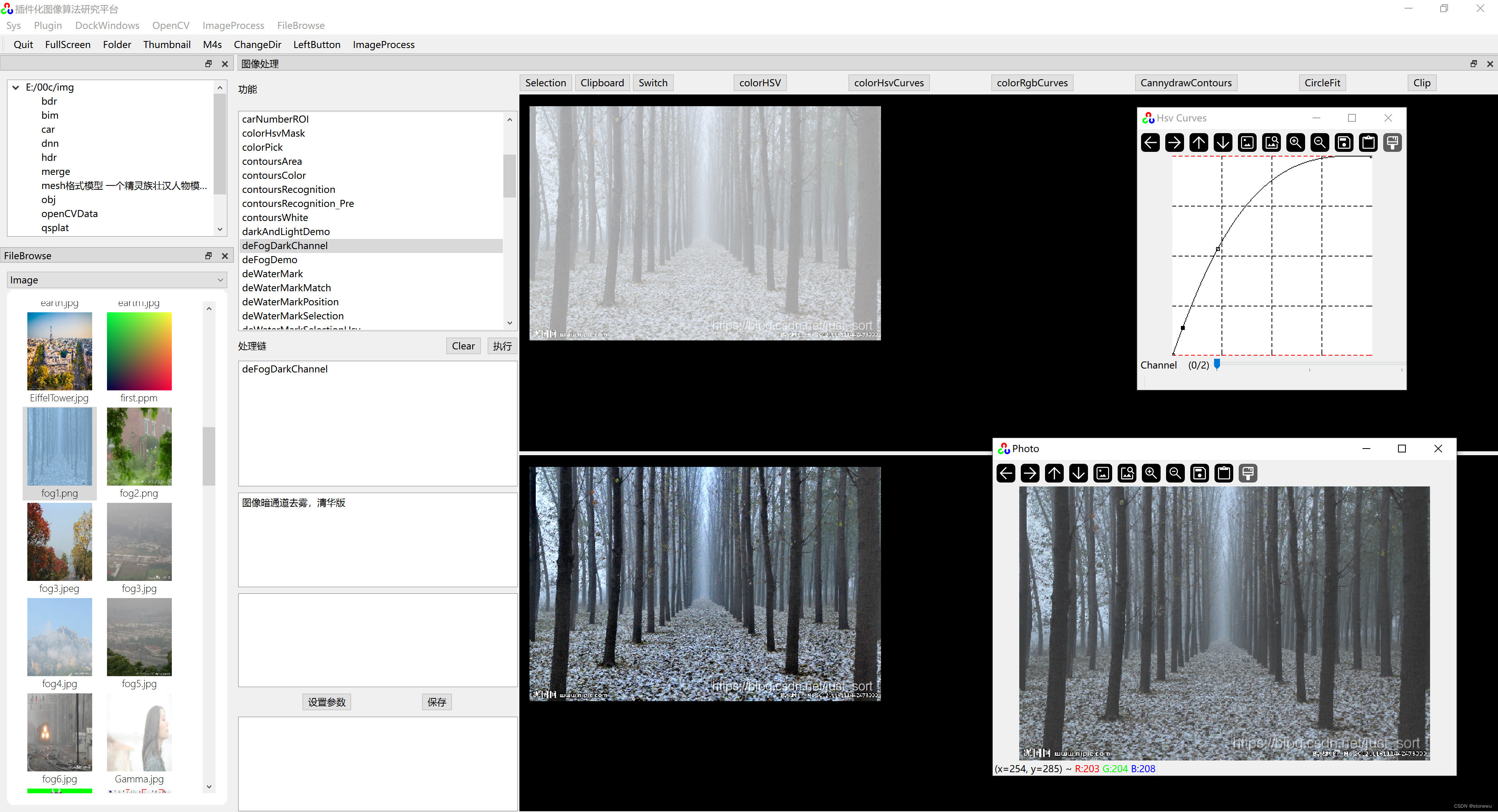
OpenCV实现Photoshop曲线调整
《QT 插件化图像算法研究平台》有仿Photoshop曲线调整图像的功能,包括RGB曲线调整和HSV曲线调整。 Photoshop曲线调整原理:RGB、HSV各通道曲线,可以理解为一个值映射(值转换)函数。X轴是输入,Y轴是输出。x0…...

【探索Linux】—— 强大的命令行工具 P.8(进程优先级、环境变量)
阅读导航 前言一、进程优先级1. 优先级概念2. Linux查看系统进程3. PRI(Priority)和NI(Nice) 二、环境变量1. 概念2. 查看环境变量方法3. 环境变量的组织方式4.通过代码获取环境变量5. 环境变量的特点 总结温馨提示 前言 前面我们…...
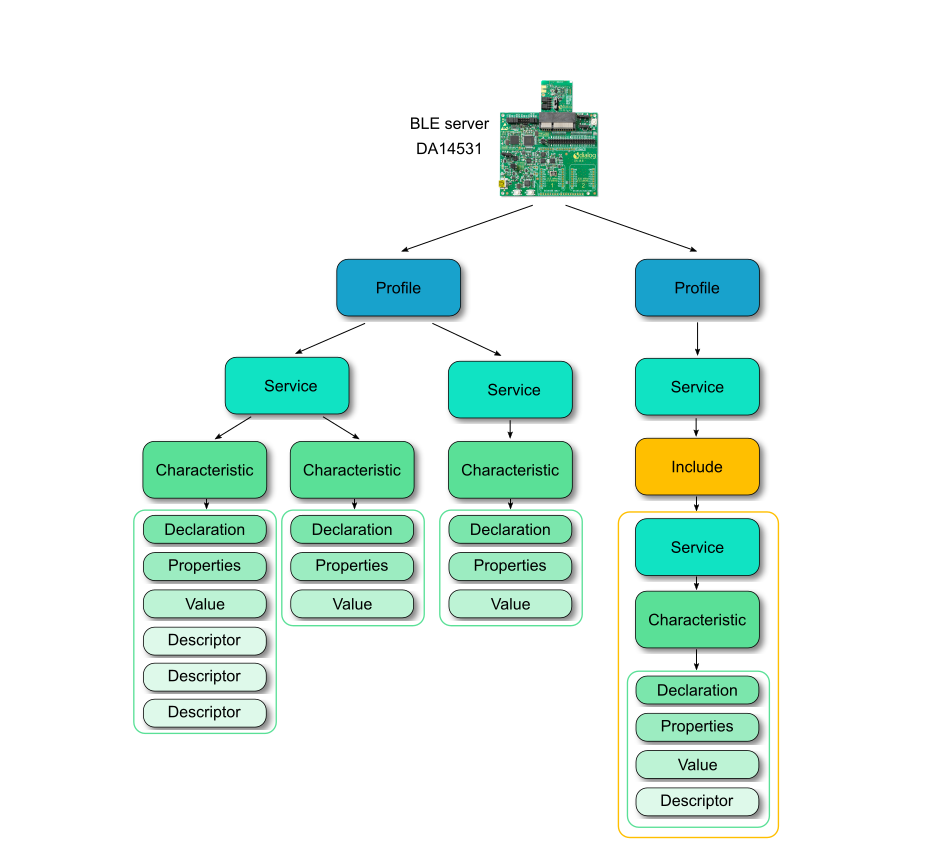
蓝牙协议栈BLE
前言 这阵子用到蓝牙比较多,想写一个专栏专门讲解蓝牙协议及其应用,本篇是第一篇文章,讲解低功耗蓝牙和蓝牙协议栈。 参考网上各大神文章,及瑞萨的文章,参考GPT,并且加入了一些本人的理解。 图片部分源自…...
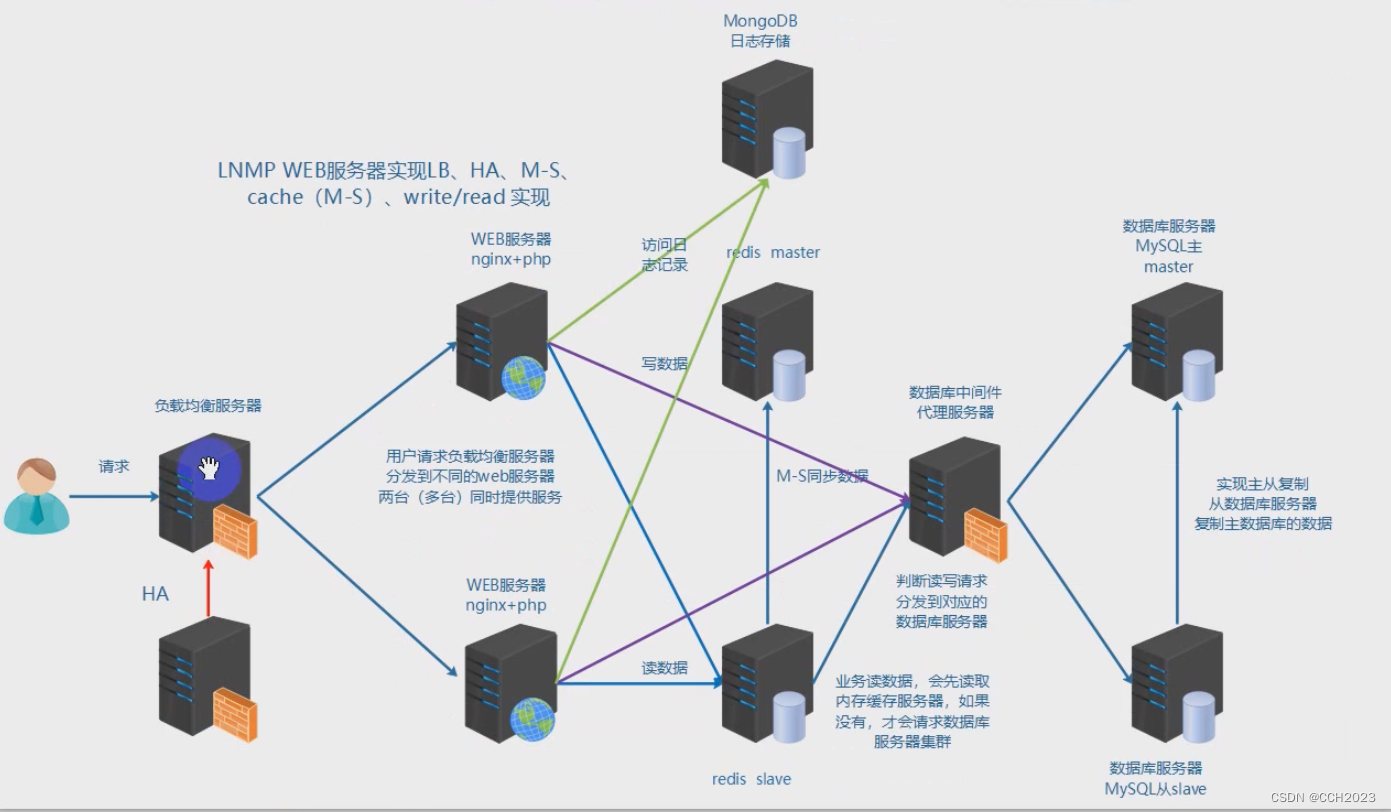
企业架构LNMP学习笔记17
反向代理: 反向代理服务器和真实访问的服务器是在一起的,有关联的。 根据实际业务需求,分发代理页面到不同的解释器。常见于代理后端服务器。 安装apache服务器: yum install -y httpd 修改配置文件: vim /et/http…...

php 获取每月开始结束时间,指定月份的开始结束时间戳
php 获取指定月份的开始结束时间戳。 /** * * 获取指定年月的开始和结束时间戳 * param int $year 年份 * param int $month 月份 * return array(开始时间,结束时间) */ function getMonthBeginAndEnd($year 0, $month 0) {$year $year ? $year : date(Y);$month $month…...
)
Docker技术入门| Part03:Dockerfile详解(Dockerfile概念、Dockerfile 指令、使用Dockerfile构建镜像)
文章目录 1. Dockerfile概念2. Dockerfile 指令FROM 指定基础镜像RUN执行命令CMD 容器启动命令COPY 复制文件ADD 更高级的复制文件ENV 设置环境变量ARG 构建参数VOLUME 定义匿名卷EXPOSE 暴露端口WORKDIR 指定工作目录USER 指定当前用户LABEL 为镜像添加元数据SHELL 指令 3. 使…...

分享一个有意思的线程相关的程序运行题
翻开之前的代码,发现了一个有意思的代码,猜以下代码的运行结果: package thread;/*** author heyunlin* version 1.0*/ public class ThreadMethodExample {public static void main(String[] args) {Thread thread new Thread(new Runnabl…...
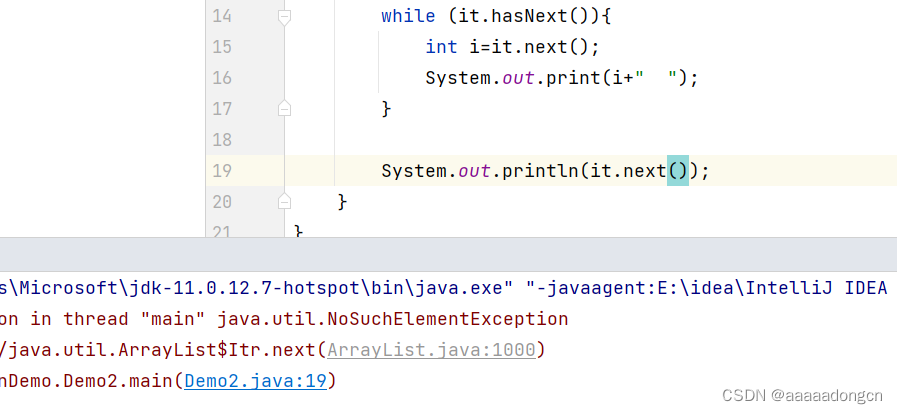
集合的进阶学习
集合体系结构 Collection 单列集合 包含List Set List 包含ArrayList LinkedList Set包含HashSet TreeSet HashSet包含LinkedHashSet List系列集合:添加的元素是有序的、可重复、有索引 Set系列集合:添加的元素是无序的、不重复、无索引 Collectio…...

Java真过饱和了吗?现在学Java迟了?
Java行业内幕揭秘 我是某有名机构的线下课Java老师,负责Java热门框架教学,如Spring、Spring MVC、Spring Boot。但最近被解雇了,让我来吐槽一下。Java现在的学习人数真的太多太多了。 Java的学习饱和度 Java学习的人太多,给你一…...

glibc2.35-通过tls_dtor_list劫持exit执行流程
前言 glibc2.35删除了malloc_hook、free_hook以及realloc_hook,通过劫持这三个hook函数执行system已经不可行了。 传统堆漏洞利用是利用任意地址写改上上述几个hook从而执行system,在移除之后则需要找到同样只需要修改某个地址值并且能够造成程序流劫持…...

linux-OpenSSL升级
1.安装编译所需的安装包 yum install -y gcc make perl zlib-devel 2.从 OpenSSL 官网下载(https://www.openssl.org/source/openssl-1.1.1v.tar.gz) 注:如果原先版本为1.x.x,升级时还是需要选择1.x.x 3. 编译安装 # 解压tar -xvf openssl-1.1.1v.tar…...
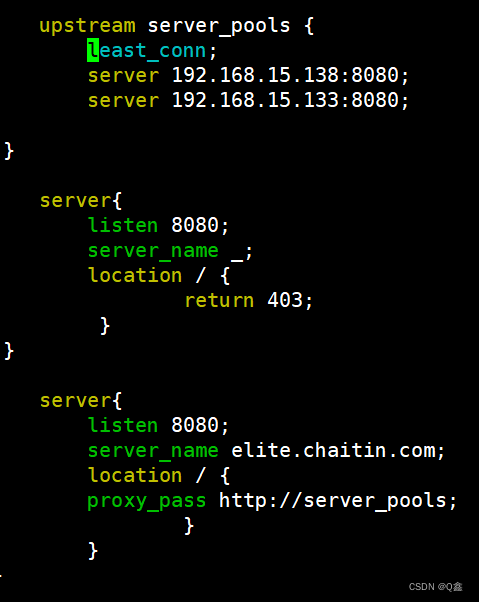
Nginx全家桶配置详解
源码包安装NGINX A,搭建Web Server,任意HTML页面,其8080端口提供Web访问服务,截图成功访问http(s)://[Server1]:8080并且回显Web页面。保留Server1,但是不允许直接访问Server 1,再部署1套NGINX …...
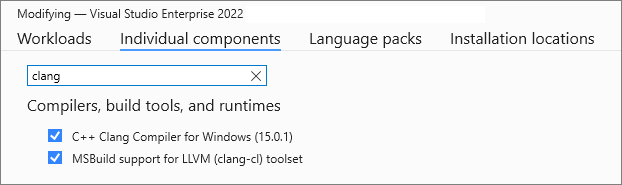
CMake生成Visual Studio工程
CMake – 生成Visual Studio工程 C/C项目经常使用CMake构建工具。CMake 项目文件(例如 CMakeLists.txt)可以直接由 Visual Studio 使用。本文要说明的是如何将CMake项目转换到Visual Studio解决方案(.sln)或项目(.vcxproj) 开发环境 为了生成Visual S…...
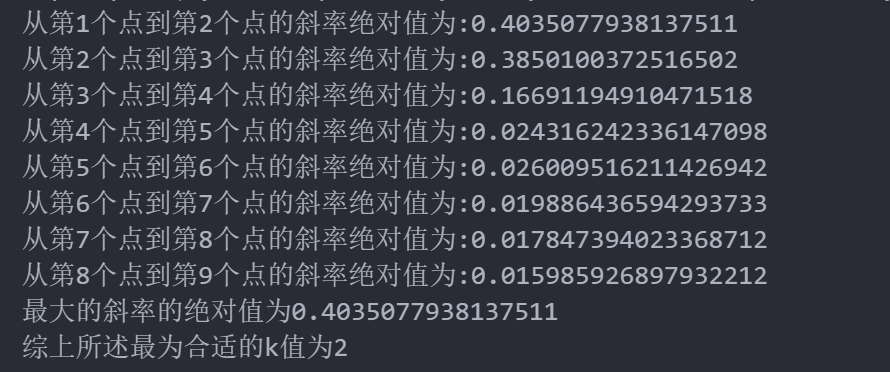
数学建模--K-means聚类的Python实现
目录 1.算法流程简介 2.1.K-mean算法核心代码 2.2.K-mean算法效果展示 3.1.肘部法算法核心代码 3.2.肘部法算法效果展示 1.算法流程简介 #k-means聚类方法 """ k-means聚类算法流程: 1.K-mean均值聚类的方法就是先随机选择k个对象作为初始聚类中心. 2.这…...

防坠安全带上亚马逊美国站要求的合规标准是什么?
防坠安全带 防坠安全带是一种防护装备,适合工人在高空作业时或在可能发生跌落的无防护边缘行走时穿着。防坠安全带设计用于包裹身体躯干,并将坠落力至少分布到大腿上部、骨盆、胸部和肩部。防坠安全带是固定物体与非固定物体之间的连接物,通…...

PDF转Word的方法分享与注意事项。
PDF和Word是两种常用的文档格式,它们各有优点,适用于不同的场景。然而,有时候我们需要将PDF转换为Word,以便更好地进行编辑和排版。本文将介绍几种常用的PDF转Word的方法,并分享一些注意事项。 一、PDF转Word的方法 使…...

gitlab配置webhook,commit message的时候校验提交的信息
在 GitLab 中配置 Webhook 来调用 Java 接口以校验 commit 信息,是很多公司的一些要求,因为提交信息的规范化是必要的 在 GitLab 项目中进入设置页面。 在左侧导航栏中选择 “Webhooks”(Web钩子)。 在 Webhooks 页面中点击 “…...

借助CIFAR10模型结构理解卷积神经网络及Sequential的使用
CIFAR10模型搭建 CIFAR10模型结构 0. input : 332x32,3通道32x32的图片 --> 特征图(Feature maps) : 3232x32即经过32个35x5的卷积层,输出尺寸没有变化(有x个特征图即有x个卷积核。卷积核的通道数与输入的通道数相等,即35x5&am…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
