数学建模--K-means聚类的Python实现
目录
1.算法流程简介
2.1.K-mean算法核心代码
2.2.K-mean算法效果展示
3.1.肘部法算法核心代码
3.2.肘部法算法效果展示
1.算法流程简介
#k-means聚类方法
"""
k-means聚类算法流程:
1.K-mean均值聚类的方法就是先随机选择k个对象作为初始聚类中心.
2.这个时候你去计算剩余的对象于哪一个聚类中心的距离是最小的,优先分配给最近的聚类中心.
3.分配后,原先的聚类中心和分配给它们的对象就又会被看作一个新聚类.
4.每次进行分配之后,聚类中心又会被重新计算一次
5.直到满足某些终止条件为止:1.没有聚类中心被分配 2.达到了局部的聚类均方误差最小
"""2.1.K-mean算法核心代码
#%%
#1.当k已知且k=4时,我们执行k-means算法
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #散点图标签可以显示中文
#人为大致创建一个比较明显的聚类样本
c1x=np.random.uniform(0.5,1.5,(1,200))
c1y=np.random.uniform(0.5,1.5,(1,200))
c2x=np.random.uniform(3.5,4.5,(1,200))
c2y=np.random.uniform(3.5,4.5,(1,200))
c3x=np.random.uniform(2.5,3.5,(1,200))
c3y=np.random.uniform(2.5,3.5,(1,200))
c4x=np.random.uniform(1.5,2.5,(1,200))
c4y=np.random.uniform(1.5,2.5,(1,200))
x=np.hstack((c1x,c2x,c3x,c4x))
y=np.hstack((c2y,c2y,c3y,c4y))
X=np.vstack((x,y)).T
#n_cluster设置成4(可以修改)
kemans=KMeans(n_clusters=4)
result=kemans.fit_predict(X) #训练及预测
for i in range(len(result)):print("第{}个点:({})的分类结果为:{}".format(i+1,X[i],result[i]))
x=[i[0] for i in X]
y=[i[1] for i in X]
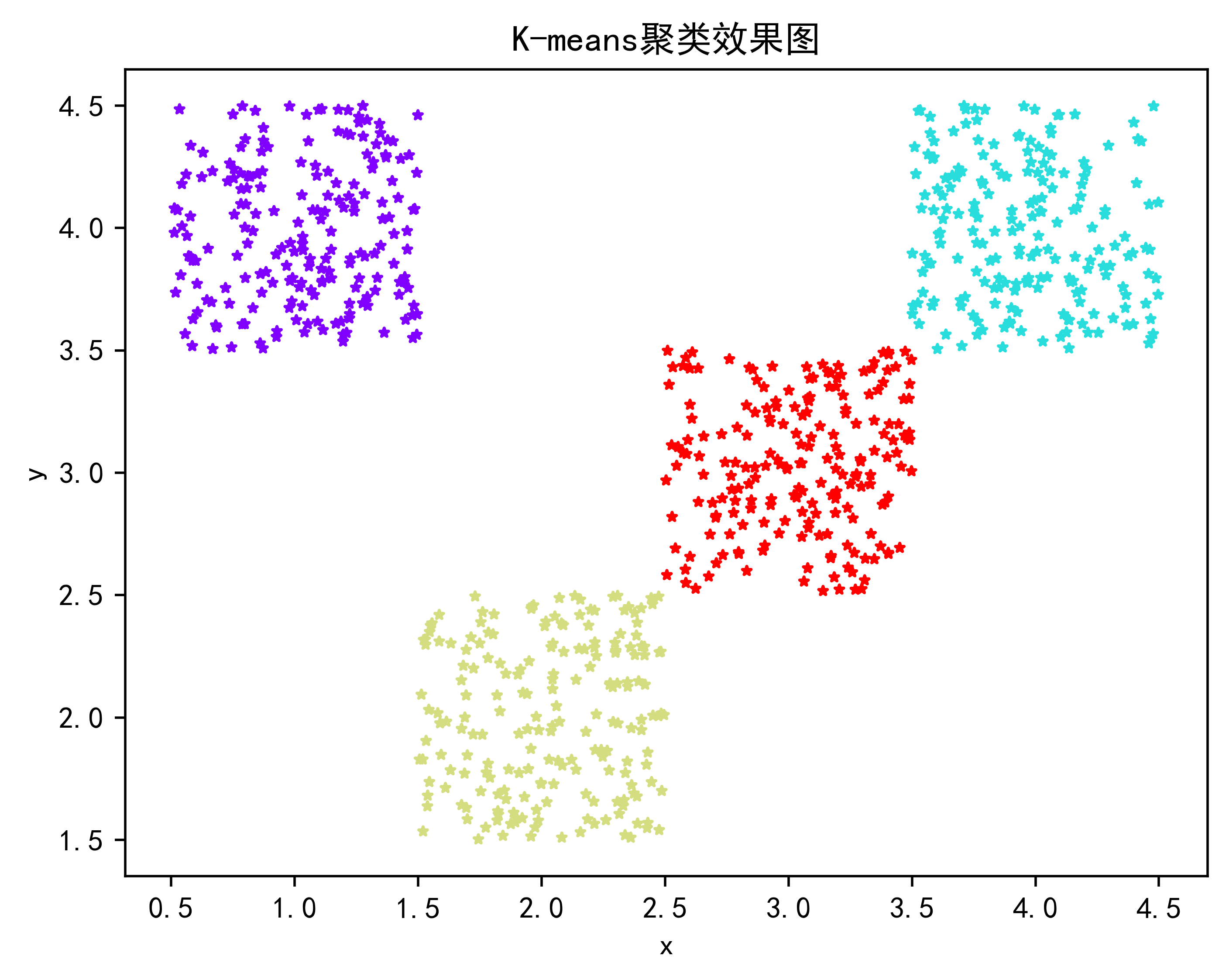
plt.scatter(x,y,c=result,marker='*',cmap='rainbow',s=9)
plt.xlabel('x')
plt.ylabel('y')
plt.title("K-means聚类效果图",color='black')
plt.savefig('C:\\Users\\Zeng Zhong Yan\\Desktop\\K-means聚类效果图.png', dpi=500, bbox_inches='tight')
plt.show()2.2.K-mean算法效果展示
3.1.肘部法算法核心代码
#%%
#2.如果k未知的情况下,利用肘部法来求出最优的k
"""
肘部法也非常简答,就是假设k=1-9,分别求出k=1-9之间的平均离差.
绘图观察最陡峭/斜率变化最大的点就是最为合适的k值
"""import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #使折线图显示中文K=range(1,10)
meanDispersions=[]
for k in K:#假设n_clusters=k,进行聚类后kemans=KMeans(n_clusters=k)kemans.fit(X)#计算平均离差m_Disp=sum(np.min(cdist(X,kemans.cluster_centers_,'euclidean'),axis=1))/X.shape[0]meanDispersions.append(m_Disp)
result=[]
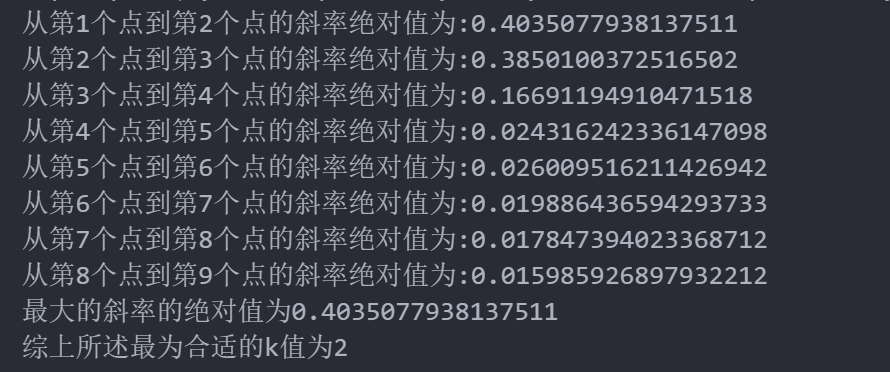
for i in range(len(meanDispersions)-1):print("从第{}个点到第{}个点的斜率绝对值为:{}".format(i+1,i+2,abs(meanDispersions[i+1]-meanDispersions[i])))result.append(abs(meanDispersions[i+1]-meanDispersions[i]))
#求解斜率最大值
result_max=max(result)
print("最大的斜率的绝对值为{}".format(result_max))
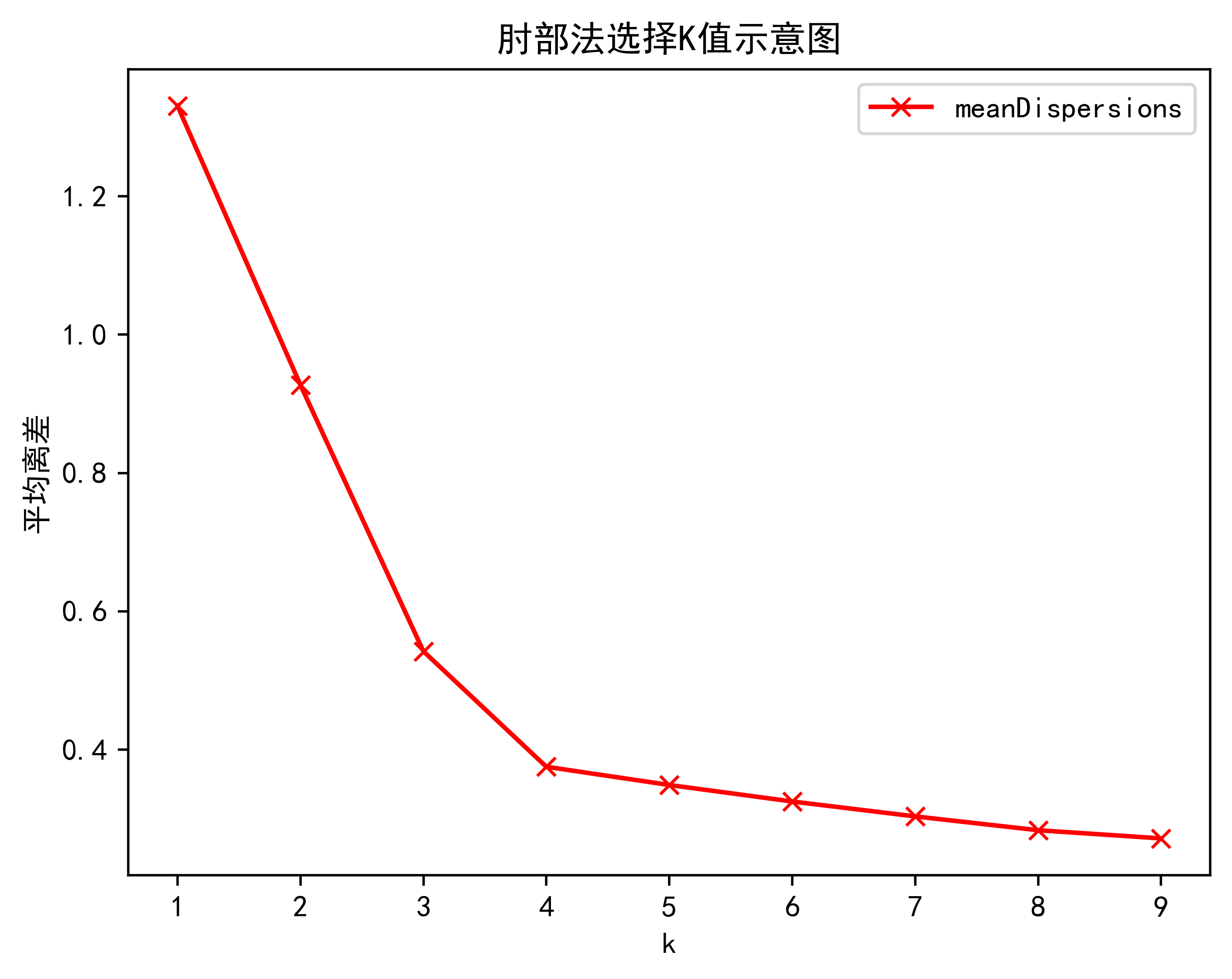
print("综上所述最为合适的k值为{}".format(result.index(result_max)+2))plt.plot(K,meanDispersions,'bx-',label='meanDispersions',color='red')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('肘部法选择K值示意图')
plt.legend()
plt.savefig('C:\\Users\\Zeng Zhong Yan\\Desktop\\肘部法求K值.png', dpi=500, bbox_inches='tight')
plt.show()3.2.肘部法算法效果展示
相关文章:

数学建模--K-means聚类的Python实现
目录 1.算法流程简介 2.1.K-mean算法核心代码 2.2.K-mean算法效果展示 3.1.肘部法算法核心代码 3.2.肘部法算法效果展示 1.算法流程简介 #k-means聚类方法 """ k-means聚类算法流程: 1.K-mean均值聚类的方法就是先随机选择k个对象作为初始聚类中心. 2.这…...

防坠安全带上亚马逊美国站要求的合规标准是什么?
防坠安全带 防坠安全带是一种防护装备,适合工人在高空作业时或在可能发生跌落的无防护边缘行走时穿着。防坠安全带设计用于包裹身体躯干,并将坠落力至少分布到大腿上部、骨盆、胸部和肩部。防坠安全带是固定物体与非固定物体之间的连接物,通…...

PDF转Word的方法分享与注意事项。
PDF和Word是两种常用的文档格式,它们各有优点,适用于不同的场景。然而,有时候我们需要将PDF转换为Word,以便更好地进行编辑和排版。本文将介绍几种常用的PDF转Word的方法,并分享一些注意事项。 一、PDF转Word的方法 使…...

gitlab配置webhook,commit message的时候校验提交的信息
在 GitLab 中配置 Webhook 来调用 Java 接口以校验 commit 信息,是很多公司的一些要求,因为提交信息的规范化是必要的 在 GitLab 项目中进入设置页面。 在左侧导航栏中选择 “Webhooks”(Web钩子)。 在 Webhooks 页面中点击 “…...

借助CIFAR10模型结构理解卷积神经网络及Sequential的使用
CIFAR10模型搭建 CIFAR10模型结构 0. input : 332x32,3通道32x32的图片 --> 特征图(Feature maps) : 3232x32即经过32个35x5的卷积层,输出尺寸没有变化(有x个特征图即有x个卷积核。卷积核的通道数与输入的通道数相等,即35x5&am…...
Java # Java基础八股
1、JVM、JRE、JDK之间的关系 个人理解:JVM可以帮助屏蔽底层的操作系统,使程序一次编译到处都可以运行,JVM可以运行class文件。JRE是java文件运行的环境,但不能新建程序,JRE包含JVM。JDK功能最齐全,包含了编…...
【Spring Boot】SpringBoot 2.6.6 集成 SpringDoc 1.6.9 生成swagger接口文档
文章目录 前言一、SpringDoc是什么?二、使用步骤1.引入库2.配置类3.访问测试 总结其他配置立个Flag 前言 之前常用的SpringFox在2020年停止更新了,新项目集成SpringFox出来一堆问题,所以打算使用更活跃的SpringDoc,这里简单介绍一…...
【算法】快速排序 详解
快速排序 详解 快速排序1. 挖坑法2. 左右指针法 (Hoare 法)3. 前后指针法4. 快排非递归 代码优化 排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性&…...

架构师spring boot 面试题
spring boot 微服务有哪些特点? Spring Boot 微服务具有以下特点: 独立性:每个微服务都是独立的部署单元,有自己的代码库和数据库。这使得微服务可以独立开发、测试、部署和扩展。 分布式:微服务架构将一个大型应用程…...

电商系统架构设计系列(十一):在电商的交易类系统中,如何正确地使用 Redis 这样的缓存系统呢?需要考虑哪些问题?
上篇文章中,我给你留了一个思考题:在电商的交易类系统中,如何正确地使用 Redis 这样的缓存系统呢?需要考虑哪些问题? 这篇文章,我们来聊聊。 引言 我们知道,大部分面向公众用户的互联网系统&a…...

MySQL数据库和表的操作
数据库基础 存储数据用文件就可以了,为什么还要弄个数据库? 文件保存数据有以下几个缺点: 1、文件的安全性问题 2、文件不利于数据查询和管理 3、文件不利于存储海量数据 4、文件在程序中控制不方便 数据库存储介质: 磁盘 内存 为了解决上…...
DAY-01--分布式微服务基础概念
一、项目简介 了解整体项目包含后端、前端、周边维护。整个项目的框架知识。 二、分布式基础概念 1、微服务 将应用程序 基于业务 拆分为 多个小服务,各小服务单独部署运行,采用http通信。 2、集群&分布式&节点 集群是个物理形态,…...

记:一次关于paddlenlp、python、版本之间的兼容性问题
兼容版本 Python 3.10.8 absl-py1.4.0 accelerate0.19.0 addict2.4.0 aiofiles23.1.0 aiohttp3.8.3 aiosignal1.3.1 alembic1.10.4 aliyun-python-sdk-core2.13.36 aliyun-python-sdk-kms2.16.0 altair4.2.2 altgraph0.17.3 aniso86019.0.1 antlr4-python3-runtime4.9.3 anyi…...

MyBatis配置及单表操作
文章目录 一. MyBatis概述二. MyBatis项目的创建1. 准备一个数据表2. 创建项目 三. MyBatis的使用1. 基本使用2. SpringBoot单元测试 四. 使用MyBatis实现单表操作1. 查询2. 修改3. 删除4. 新增 五. 基于注解完成SQL 一. MyBatis概述 MyBatis 是一款优秀的持久层框架ÿ…...

python基础教程:深浅copy的详细用法
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 1.先看赋值运算 l1 [1,2,3,[barry,alex]] l2 l1l1[0] 111 print(l1) # [111, 2, 3, [barry, alex]] print(l2) # [111, 2, 3, [barry, alex]]l1[3][0] wusir print(l1) # [111, 2, 3, [wusir, alex]] print(l2)…...
【算法篇】动态规划(二)
文章目录 分割回文字符串编辑距离不同的子序列动态规划解题思路 分割回文字符串 class Solution { public:bool isPal(string& s,int begin,int end){while(begin<end){if(s[begin]!s[end]){return false;}begin;end--;}return true;}int minCut(string s) {int lens.si…...
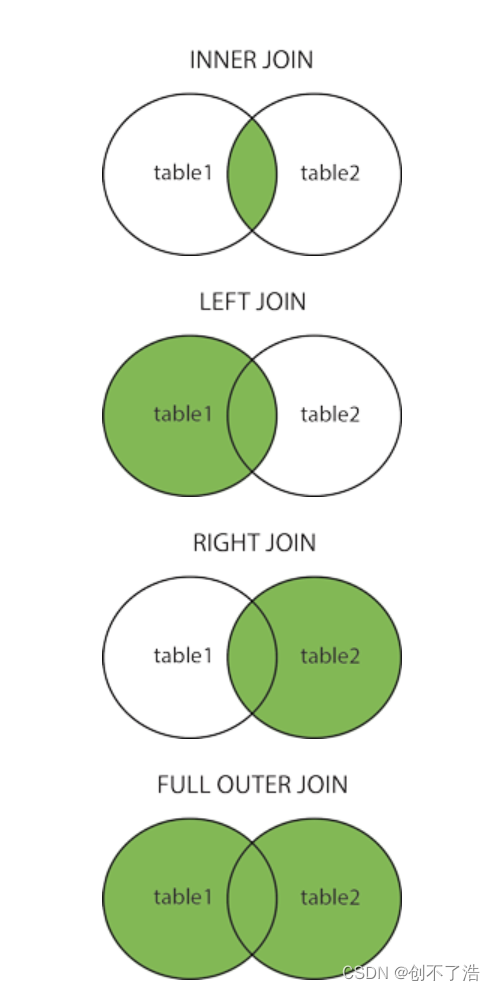
数据库 SQL高级查询语句:聚合查询,多表查询,连接查询
目录 创建学生表聚合查询聚合函数直接查询设置别名查询设置条件查询 常用的聚合函数 分组查询单个字段Group by报错分组查询多字段分组查询 多表查询直接查询重命名查询Students表新建一列CourseID 连接(JOIN)查询INNER JOINRIGHT JOIN, LEFT JOINFULL J…...

pytorch-构建卷积神经网络
构建卷积神经网络 卷积网络中的输入和层与传统神经网络有些区别,需重新设计,训练模块基本一致 import torch import torch.nn as nn import torch.optim as optim import torch.nn.functional as F from torchvision import datasets,transforms impor…...
)
点云从入门到精通技术详解100篇-点云滤波算法及单木信息提取(续)
目录 3.3 点云滤波算法原理概述 3.3.1 坡度滤波算法 3.3.2 基于不规则三角网滤波 3.3.3 数学形态学滤波...

Gartner发布中国科技报告:数据编织和大模型技术崭露头角
近日,全球知名科技研究和咨询机构Gartner发布了关于中国数据分析与人工智能技术的最新报告。报告指出,中国正迎来数据分析与人工智能领域的蓬勃发展,预计到2026年,将有超过30%的白领工作岗位重新定义,生成式人工智能技…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...