无穷级数重要知识点
- 部分和
s = ∑ i = 1 n u i s = \sum_{i=1}^{n} u _{i} s=i=1∑nui
注意:部分和不是数列的一部分之和,而是一个极限的概念,此处的n是一个极限值, n 趋于正无穷! \color{red}n趋于正无穷! n趋于正无穷!一定要注意。
- 调和级数
1 + 1 2 + 1 3 + 1 4 + 1 5 + . . . + 1 n − 2 + 1 n − 1 + 1 n (1.1) 1 + \frac{1}{2} + \frac{1}{3} +\frac{1}{4} +\frac{1}{5} +... + \frac{1}{n-2} + \frac{1}{n-1} + \frac{1}{n} \tag{1.1} 1+21+31+41+51+...+n−21+n−11+n1(1.1)
调和级数可以化为如下积分式:
∫ 1 + ∞ 1 x d x = ln x ∣ 1 + ∞ = ∞ \int_{1}^{+\infty} \frac{1}{x}dx = \ln x |_{1}^{+\infty} = \infty ∫1+∞x1dx=lnx∣1+∞=∞
可见调和级数发散。
调和级数是一个重要级数,是判断其他级数收敛的参考。若一个级数大于调和级数,则必定发散,若一个级数是调和级数的无穷小,则一定收敛。
- 级数收敛的必要非充分条件
若级数 ∑ i = 1 + ∞ u i \sum_{i= 1}^{+\infty} u_{i} ∑i=1+∞ui收敛,则一般项 u i u_{i} ui的极限为0。
此条件是级数收敛的必要条件而非充分条件。比如调和级数的一般项为0但是并不收敛。
- 达朗贝尔判别法
正向级数 ∑ i = 1 + ∞ u i 若 lim i → + ∞ u i + 1 u i > 1 则级数发散 若 lim i → + ∞ u i + 1 u i < 1 则级数收敛 若 lim i → + ∞ u i + 1 u i = 1 则无法判别敛散性 \color{red}正向级数\sum_{i= 1}^{+\infty} u_{i} \\ 若\lim_{i \to +\infty} \frac{u_{i+1}}{u_{i}} > 1则级数发散\\ 若\lim_{i \to +\infty} \frac{u_{i+1}}{u_{i}} < 1则级数收敛\\ 若\lim_{i \to +\infty} \frac{u_{i+1}}{u_{i}} =1则无法判别敛散性 正向级数i=1∑+∞ui若i→+∞limuiui+1>1则级数发散若i→+∞limuiui+1<1则级数收敛若i→+∞limuiui+1=1则无法判别敛散性
证明:
(1)若 lim i → + ∞ u i + 1 u i = ρ > 1 , 即 u i + 1 > u i , 即 u i + 1 = k u i , k > 1 \lim_{i \to +\infty} \frac{u_{i+1}}{u_{i}} =\rho >1, 即u_{i+1} >u_{i}, 即u_{i+1} = ku_{i},k> 1 limi→+∞uiui+1=ρ>1,即ui+1>ui,即ui+1=kui,k>1
(2)若 lim i → + ∞ u i + 1 u i = ρ < 1 , 即 u i + 1 < u i , 即 u i + 1 = k u i , k < 1 \lim_{i \to +\infty} \frac{u_{i+1}}{u_{i}} =\rho <1, 即u_{i+1} <u_{i}, 即u_{i+1} = ku_{i},k < 1 limi→+∞uiui+1=ρ<1,即ui+1<ui,即ui+1=kui,k<1
通过考察等比数列(几何级数)的求和公式: a 1 1 − q n 1 − q a_{1}\frac{1-q^{n}}{1- q} a11−q1−qn
当公比q大于1时,几何级数发散,当q小于1时几何级数收敛于 a 1 1 1 − q a_{1} \frac{1}{1-q} a11−q1。
故达朗贝尔判别法得证。
- 柯西判别法
正向级数 ∑ i = 1 + ∞ u i 若 lim i → + ∞ n n > 1 则级数发散 若 lim i → + ∞ n n < 1 则级数收敛 若 lim i → + ∞ n n = 1 则无法判别敛散性 \color{red}正向级数\sum_{i= 1}^{+\infty} u_{i} \\ 若\lim_{i \to +\infty} \sqrt [n] n> 1则级数发散\\ 若\lim_{i \to +\infty}\sqrt [n] n < 1则级数收敛\\ 若\lim_{i \to +\infty} \sqrt [n] n =1则无法判别敛散性 正向级数i=1∑+∞ui若i→+∞limnn>1则级数发散若i→+∞limnn<1则级数收敛若i→+∞limnn=1则无法判别敛散性
证明方式也参考达朗贝尔判别法。
5. 极限审敛法
正向级数 ∑ i = 1 + ∞ u i 若 lim i → + ∞ n u i = l > 0 则级数发散 若 lim i → + ∞ n p u i = l > = 0 ( p > 1 ) 则级数收敛 \color{red}正向级数\sum_{i= 1}^{+\infty} u_{i} \\ 若\lim_{i \to +\infty} n u_{i} = l > 0则级数发散\\ 若\lim_{i \to +\infty} n^p u_{i} = l >= 0(p > 1)则级数收敛 正向级数i=1∑+∞ui若i→+∞limnui=l>0则级数发散若i→+∞limnpui=l>=0(p>1)则级数收敛
- 例题
讨论p级数的敛散性:
1 + 1 2 p + 1 3 p + 1 4 p + . . . + 1 ( n − 1 ) p + 1 n p 1 + \frac{1}{2^p}+ \frac{1}{3^p}+ \frac{1}{4^p}+ ... + \frac{1}{(n-1)^p}+ \frac{1}{n^p} 1+2p1+3p1+4p1+...+(n−1)p1+np1
相关文章:

无穷级数重要知识点
部分和 s ∑ i 1 n u i s \sum_{i1}^{n} u _{i} si1∑nui 注意:部分和不是数列的一部分之和,而是一个极限的概念,此处的n是一个极限值, n 趋于正无穷! \color{red}n趋于正无穷! n趋于正无穷&#x…...

【MyBatis】快速入门
1、简介 MyBatis是一个持久化、轻量级的半自动化ORM框架,封装了所有JDBC的原始操作。查询参数以及获取结果集等。 1.1 原始JDBC操作存在的问题 (1)数据库连接、释放频繁造成系统资源浪费,影响系统性能 (2)…...
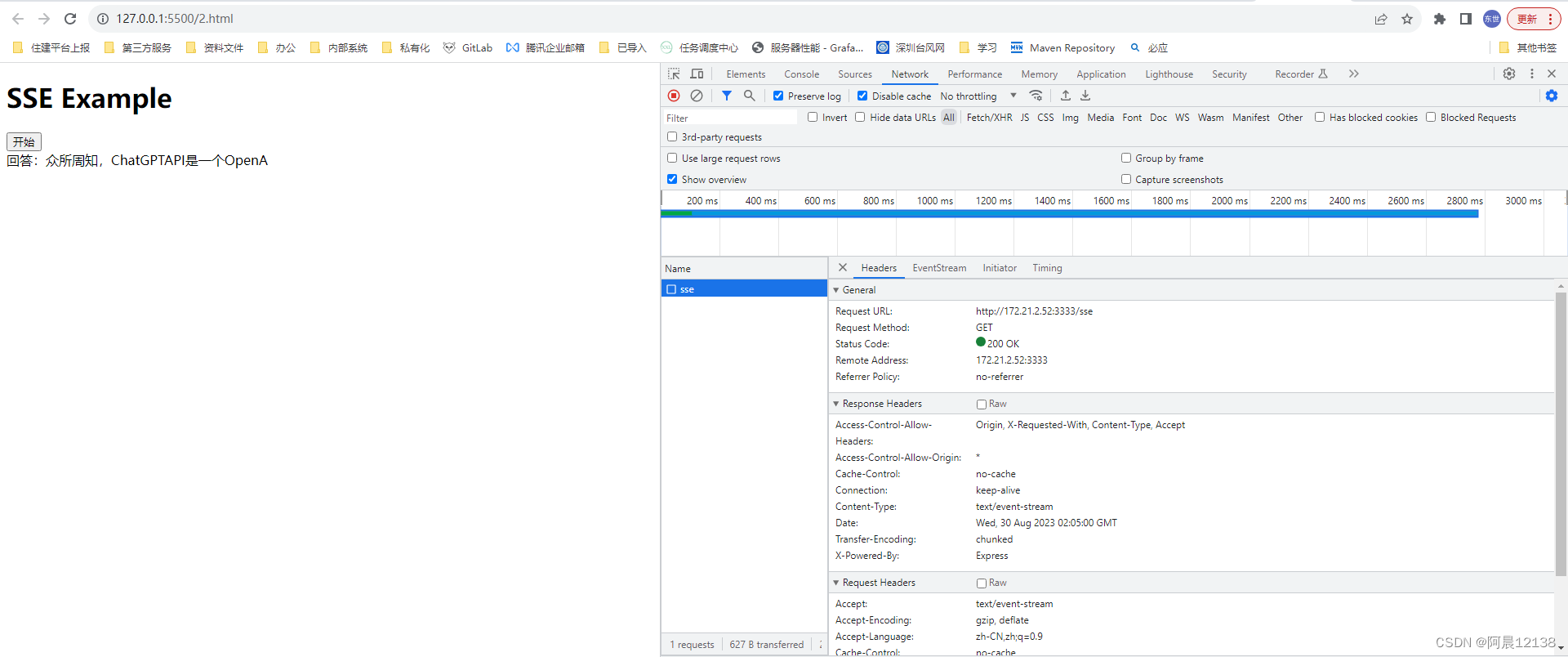
【gtpJavaScript】使用JavaScript实现套壳gtp与gtp打字输出效果
postman测试gtp接口 https://platform.openai.com/docs/api-reference/chat/create?langcurl 导入到postman中 记得弄一个gtp的key 然后请求测试gtp接口: 纯前端实现gtp请求页面 目录结构: 部分参考:GitHub - xxxjkk/chat-website: 简易版c…...
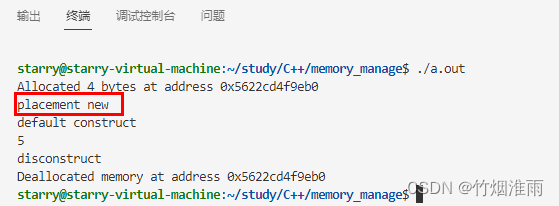
C++内存管理(2)new、delete详解
目录 new operator(new操作) new类对象时加不加括号的差别 new工作任务 delete工作任务 new和delete 堆区空间操作(对比malloc和free) new和delete操作基本类型的空间 new和delete操作基本类型的数组 new和delete操作类的…...
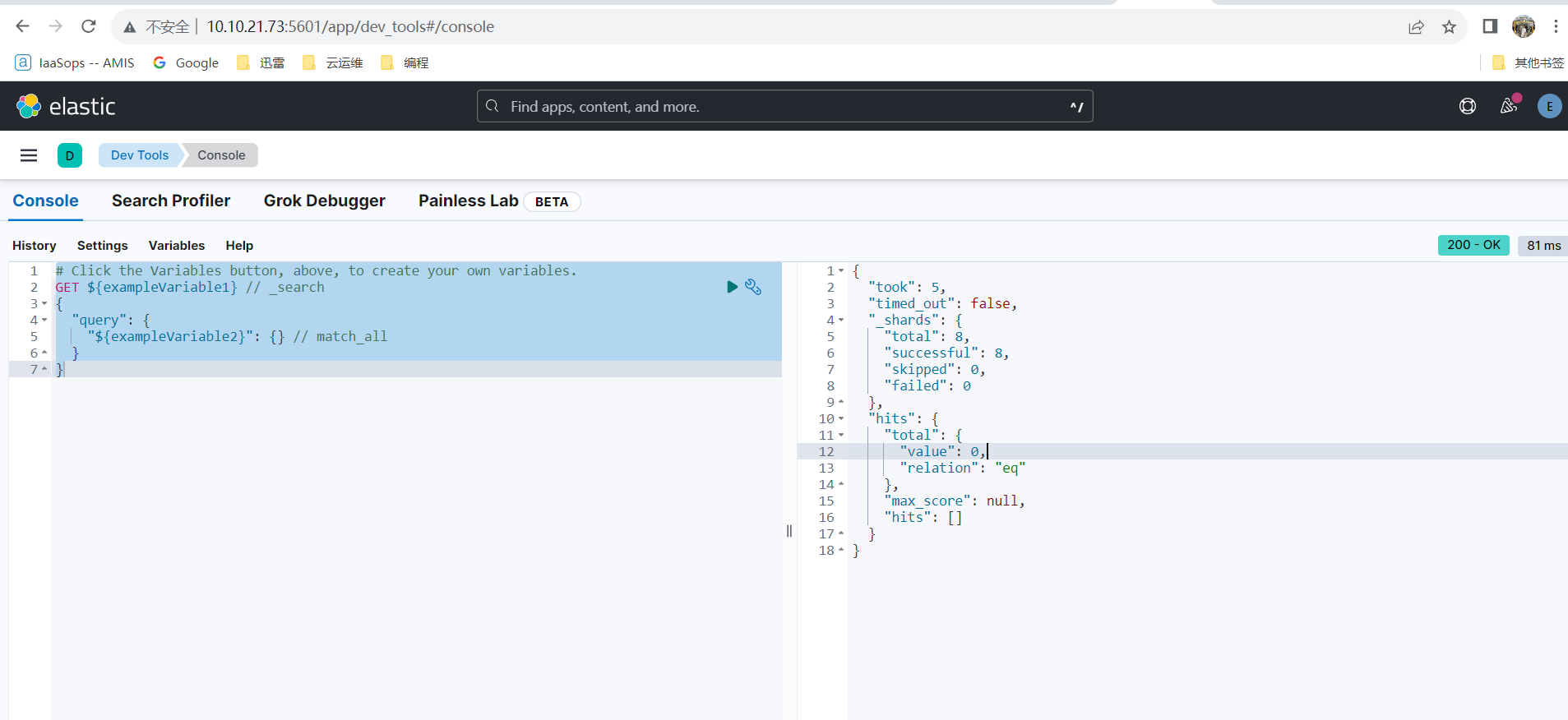
ELK集群搭建流程(实践可用)
一、概述 ELK 是一个由三个开源软件工具组成的数据处理和可视化平台,包括 Elasticsearch、Logstash 和 Kibana。这些工具都是由 Elastic 公司创建和维护的。 Elasticsearch 是一个分布式的搜索和分析引擎,可以将大量数据存储在一个或多个节点上…...

react-quill富文本 中文输入法触发change问题
使用的富文本是编辑器 react-quill 需求: 点击按钮插入自定义颜色文字,然后手动输入为正常颜色。 问题: quill组件把带颜色的字体创建个dom, 临近的文字都会整合进一个dom中,导致输入的文字和插入的带颜色 都统一成一个颜色了…...
Upload-labs 1~15 通关详细教程
文章目录 Upload-labs 1~15 通关详细教程Pass-01-前端js验证Pass-02-后端MIME验证Pass-03-黑名单验证Pass-04-黑名单验证.htaccessPass-05-文件后缀名大小写绕过Pass-06-文件后缀名空格绕过Pass-07-文件后缀名点绕过Pass-08-文件后缀名::$DATA绕过Pass-09-点空格点空格绕过Pass…...

ChatGPT分析日本排放核污水对世界的影响
文章目录 1 背景2 环境影响3 健康影响4 国际关系影响5 应对措施 近段时间被日本排放核污水到海里的消息刷屏了,这一举措引发了广泛的关注和担忧。本文结合ChatGPT来分析这件事的前因后果、会对世界造成的影响、以及应对措施。 1 背景 受2011年发生的大地震及海啸影响…...
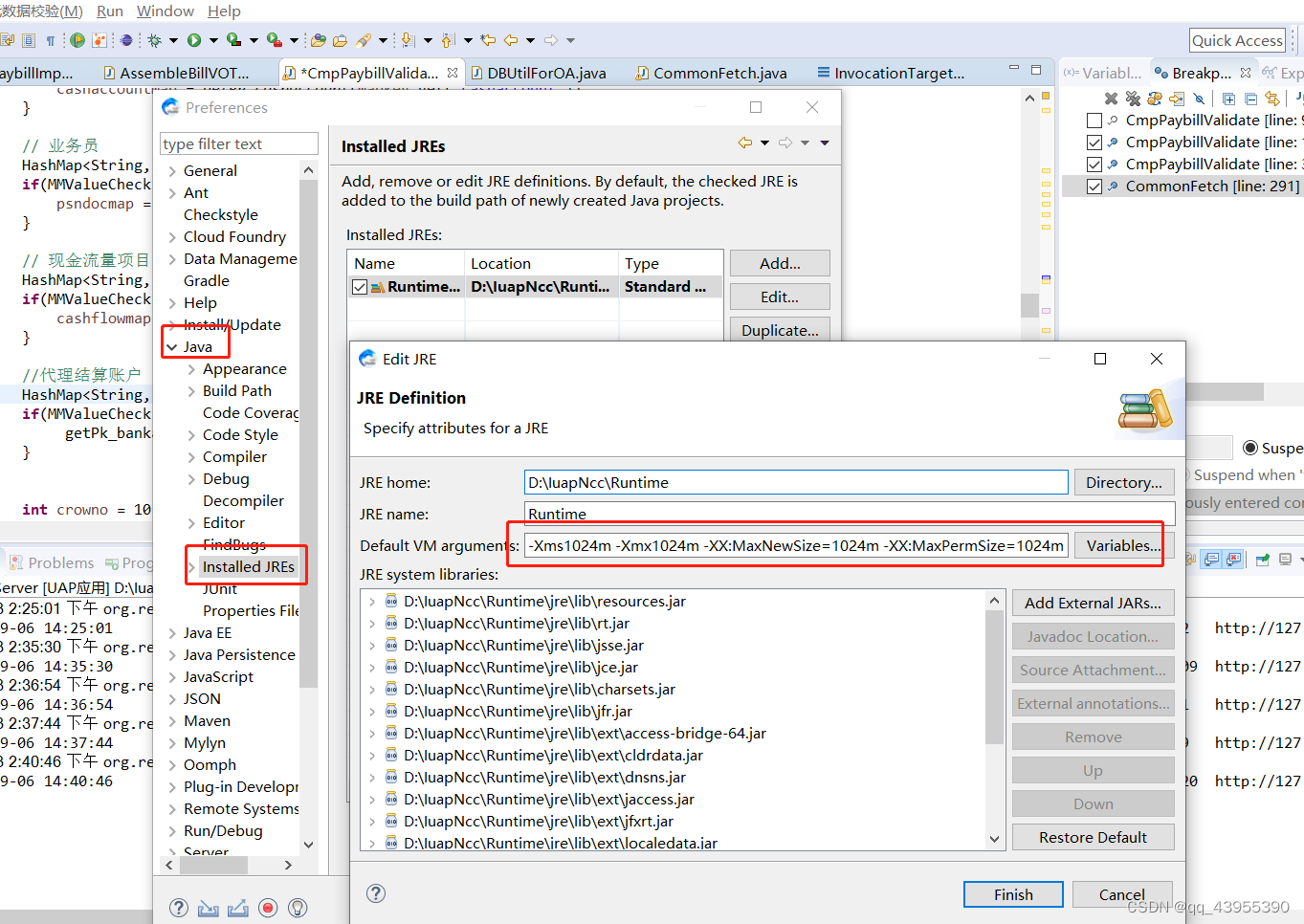
eclipse进入断点之后,一直卡死,线程一直在运行【记录一种情况】
问题描述: 一直卡死在某个断点处,取消断点也是卡死在这边的进程处。 解决方式: 将JDK的使用内存进行了修改 ① 打开eclipse,window->preference->Java->Installed JREs,选中使用的jdk然后点击右侧的edit,在…...
)
2.5 动态字符串 String (完整源码)
C自学精简教程 目录(必读) C数据结构与算法实现(目录) 本文的实现基本上和 动态数组 vector 是一样的。 因为大部分接口都一样。 所以,本文就直接给出全部的源码和运行结果。 //------下面的代码是用来测试你的代码有没有问题的辅助代码…...
Ansible之变量
一)Ansible变量介绍 我们在PlayBook⼀节中,将PlayBook类⽐成了Linux中的shell。 那么它作为⼀⻔Ansible特殊的语⾔,肯定要涉及到变量定义、控 制结构的使⽤等特性。 在这⼀节中主要讨论变量的定义和使⽤ 二)变量命名规则 变量的…...
自动化测试面试常见技术题目
1:一行代码实现1--100之和 print(sum(list(range(1,101)))) 2:如何在一个函数内部修改全局变量 global 修改全局变量 局部作用域只能调用全局作用域的变量,但是不熊修改全局作用域的变量,如果想要修改全局作用域的变量需要gl…...

aarch64 arm64 部署 stable diffusion webui 笔记 【2】继续安装其他依赖 gfpgan
接上篇 aarch64 arm64 部署 stable diffusion webui 笔记 【1】准备 venv 安装pytorch 验证cuda_hkNaruto的博客-CSDN博客 编辑requirements_versions.txt,注释掉torch 启动webui.sh (venv) [rootceph3 stable-diffusion-webui]# useradd yeqiang useradd…...
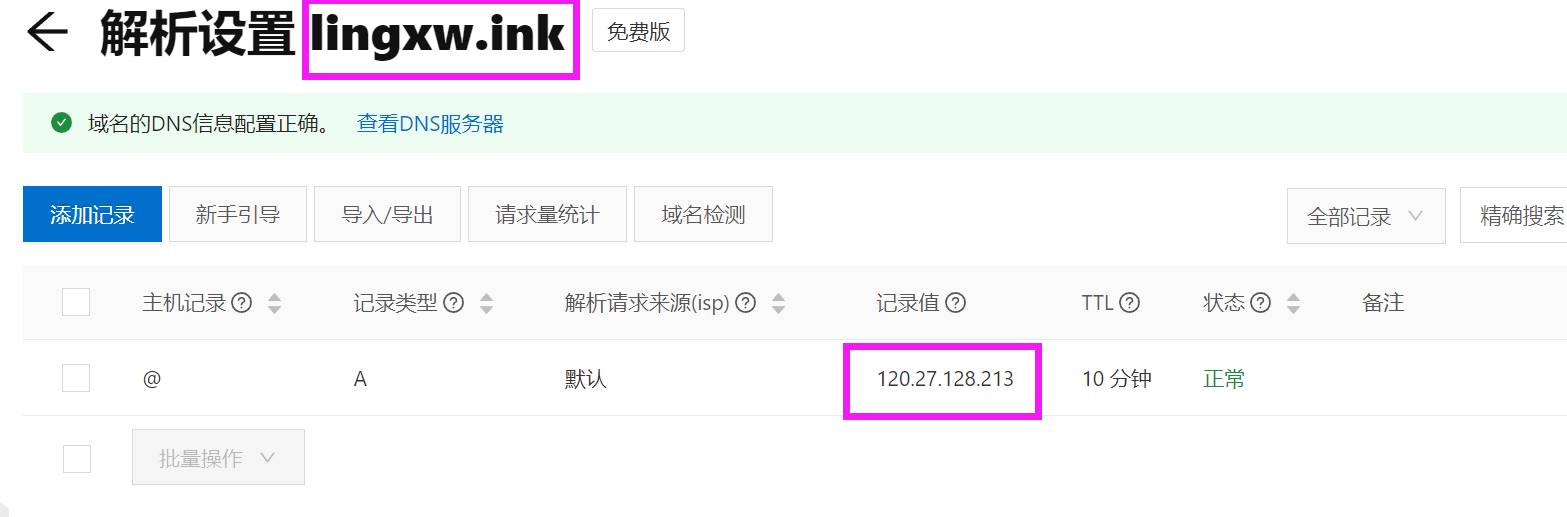
使用ECS和RDS部署WordPress,搭建个人博客并使用域名访问
目录 一、准备工作 1、准备ECS服务器 2、创建数据库账号和密码 二、部署环境 1、远程连接 2、安装Apache服务 3、部署WordPress 三、对博客的优化并使用域名访问 1、博客的设计优化 1.1 插件的使用 1.2 博客的设计介绍 2、使用域名访问 四、个人博客部署的心得 1…...
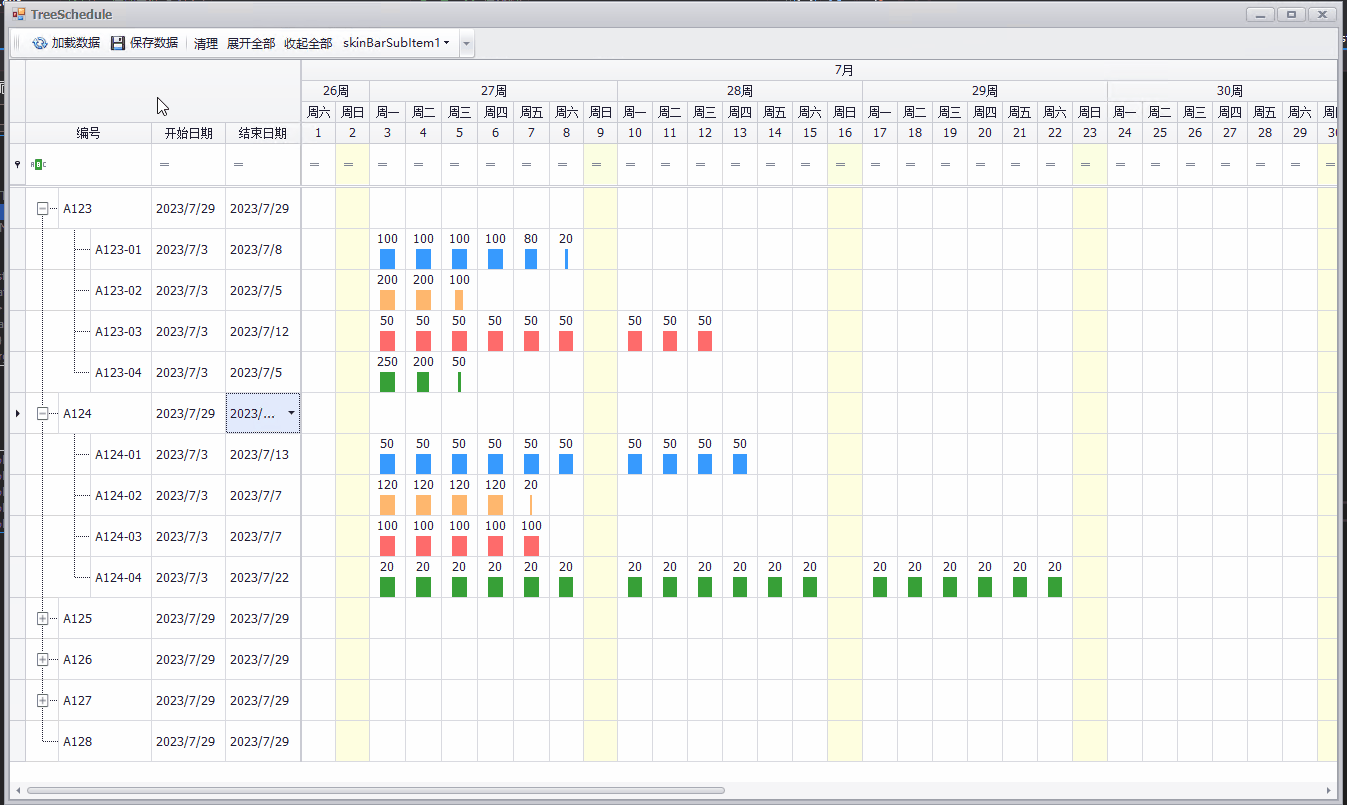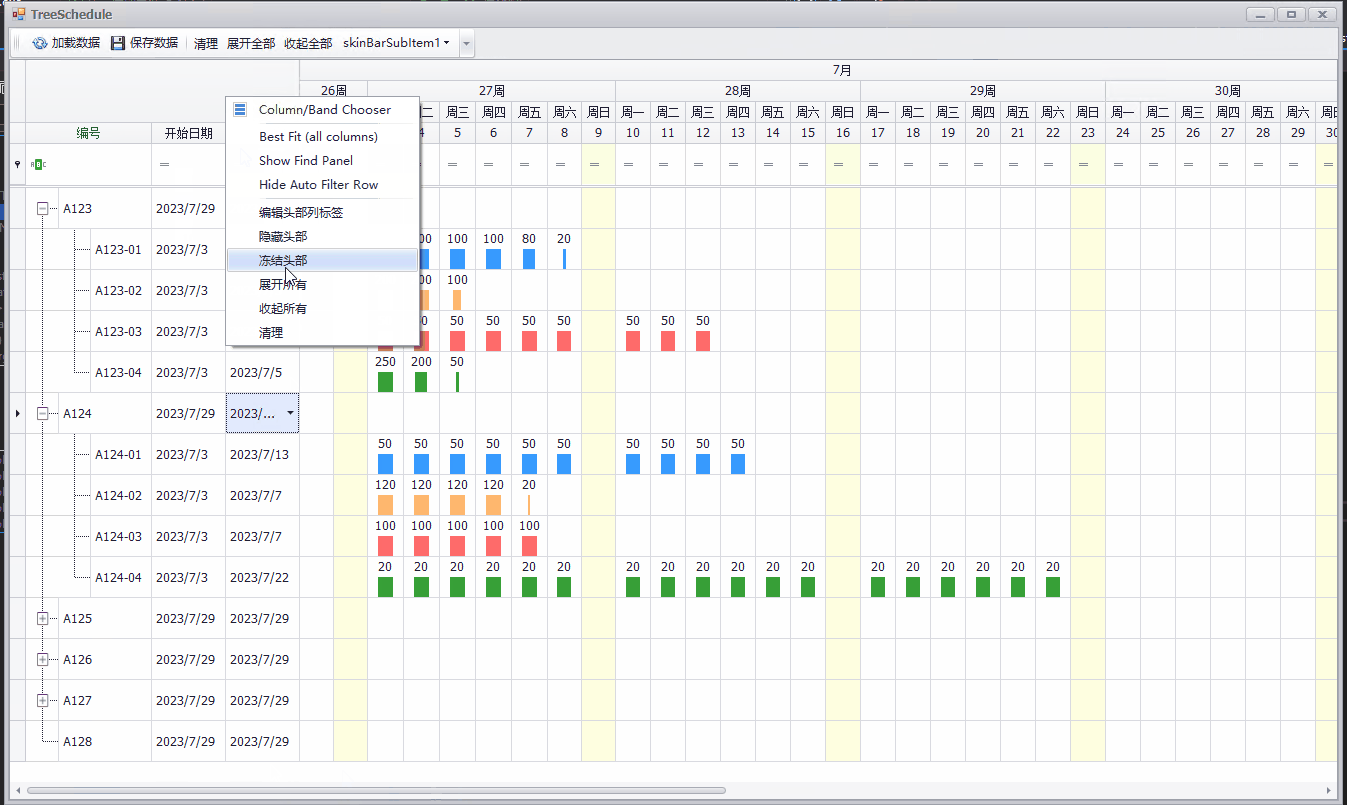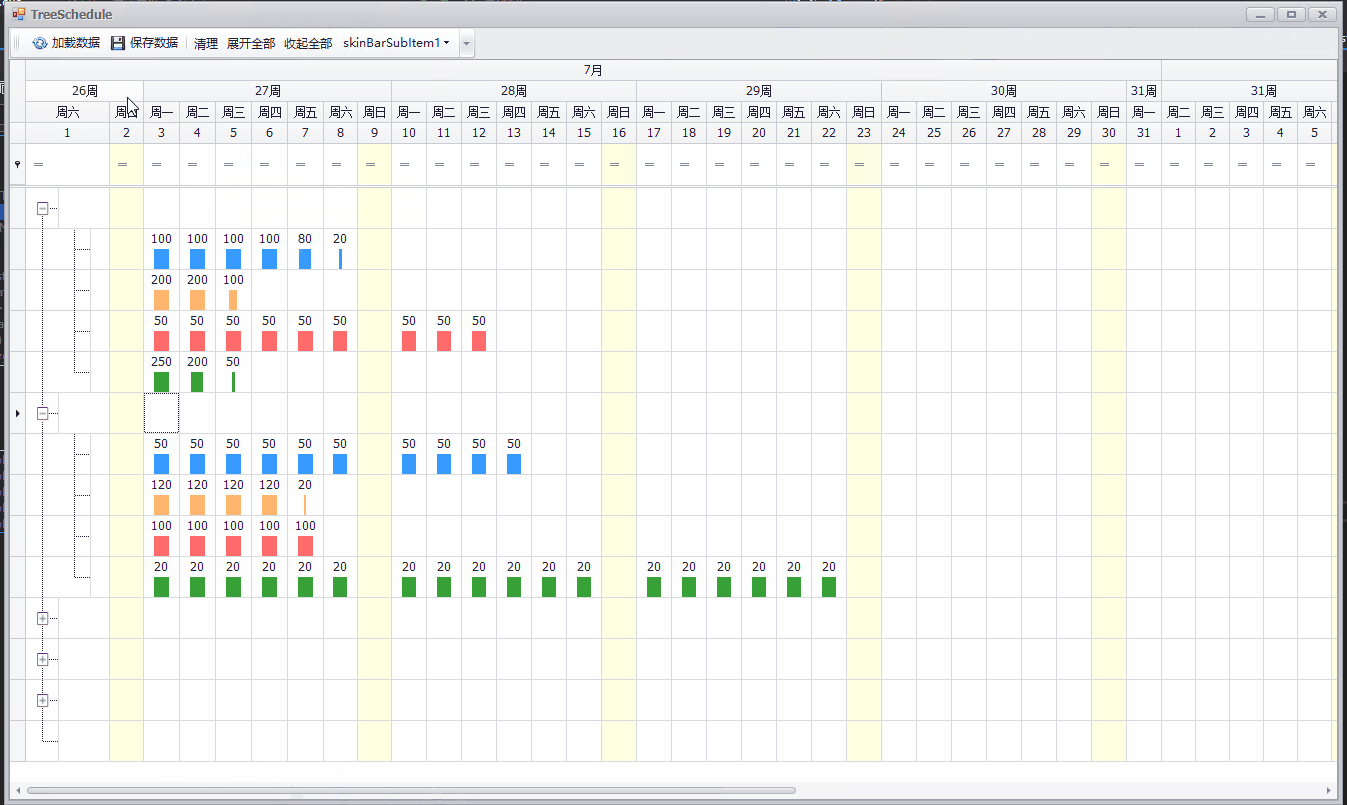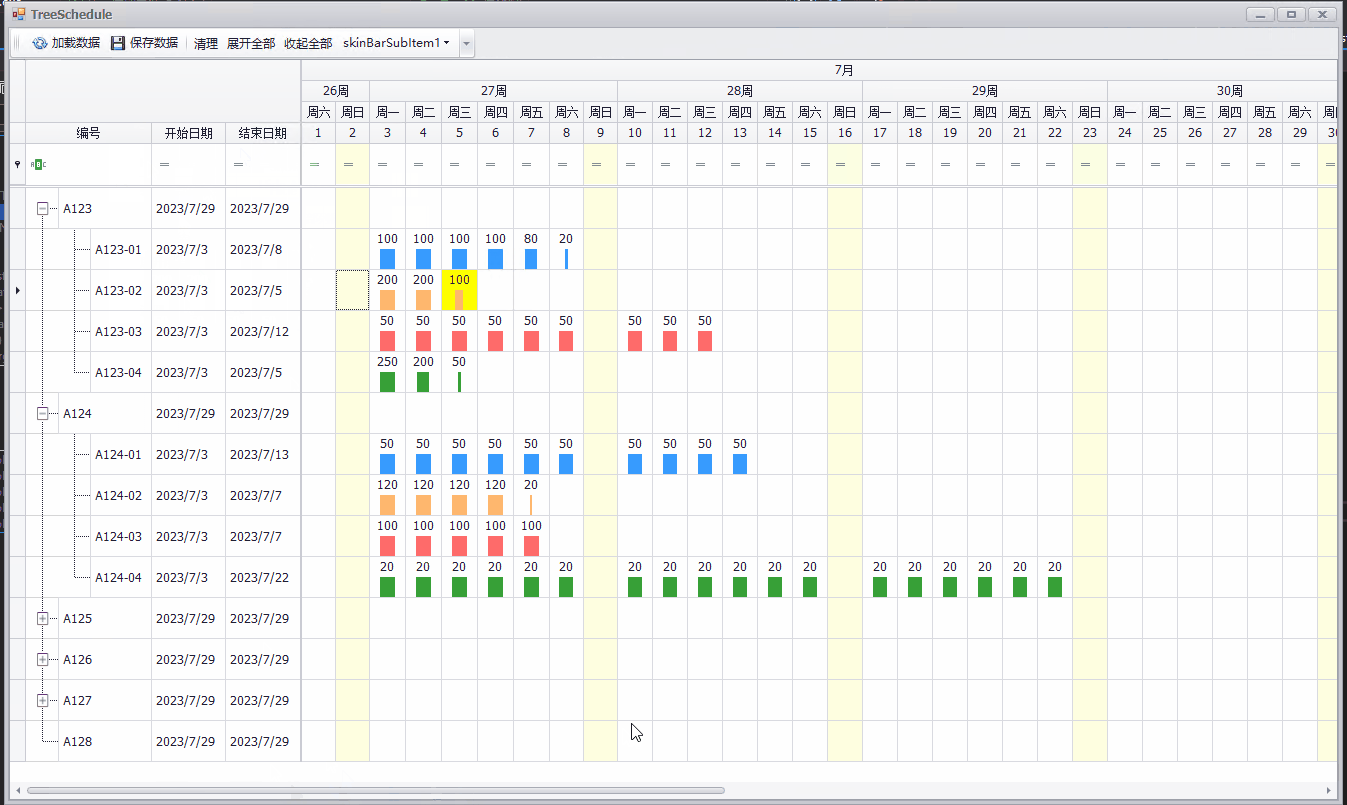
C# Winform 简单排期实现(DevExpress TreeList)
排期的需求在很多任务安排的系统中都有相应的需求,原生的Winform控件并未提供相应的控件,一般都是利用DataGridViewTreeView组合完成相应的需求,实现起来比较麻烦。用过DevExpress控件集的开发者应该知道,DevExpress WinForm提供了…...
)
2023高教社杯国赛数学建模C题思路+模型+代码(9.7晚开赛后第一时间更新)
目录 1.C题思路模型:9.7晚上比赛开始后,第一时间更新,获取见文末名片 2.竞赛注意事项:包括比赛流程,任务分配,时间把控,论文润色,已经发布在文末名片中 3.常用国赛数学建模算法 …...

QT6中添加串口模块SerialPort最简单方法
qt6.2.3以上版本已经开始支持SerialPort包了,不用在傻傻的自己去编译包了。 在安装的时候勾选SerialPort即可。 等着安装完即可。 如果已经安装完了的小伙伴,可以用 从新打开维护 选择增加或者删除组件 即可从新选择组件...
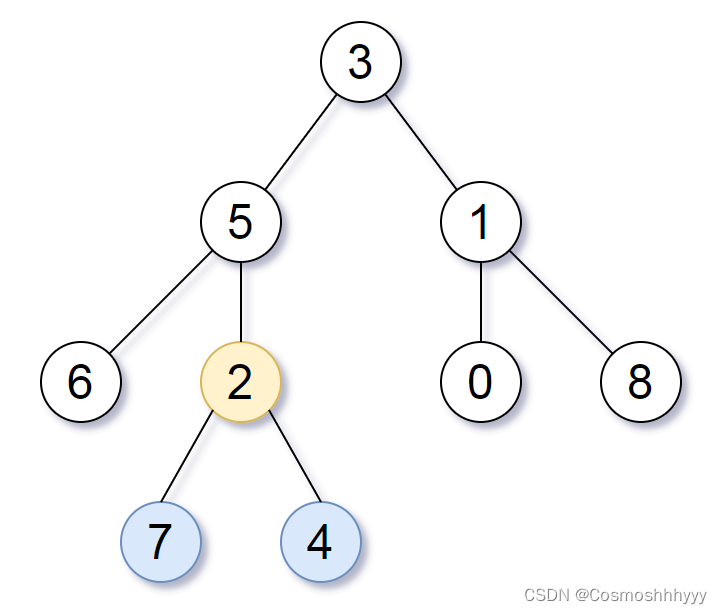
LeetCode每日一题:1123. 最深叶节点的最近公共祖先(2023.9.6 C++)
目录 1123. 最深叶节点的最近公共祖先 题目描述: 实现代码与解析: dfs 原理思路: 1123. 最深叶节点的最近公共祖先 题目描述: 给你一个有根节点 root 的二叉树,返回它 最深的叶节点的最近公共祖先 。 回想一下&…...

Oracle查看锁表和正在执行的Sql
查看当前被锁的表(需要有管理员权限): --查看锁表进程SQL语句1: select sess.sid,sess.serial#,lo.oracle_username,lo.os_user_name,ao.object_name,lo.locked_modefrom v$locked_object lo, dba_objects ao, v$session sesswh…...

Linux centos 卸载 ceph
在CentOS上卸载Ceph的操作步骤: 1. 停止Ceph集群:首先,你需要停止Ceph集群中的所有服务。在每个节点上运行以下命令来停止所有服务 systemctl stop ceph.target 2. 卸载Ceph软件包:在每个节点上,使用yum包管理器卸载C…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
