HashMap源码阅读解惑
HashMap的hash函数(1.8)
首先1.7的是四次扰动,1.8做了优化。
简单的说就是对key做hashCode操作,然后将得到的32为散列值向右位移16位,再与hashCode做异或计算。实质上是把一个数的低16位与他的高16位做异或运算。
static final int hash(Object key) {int h;return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}首先 h = key.hashCode()是key对象的一个hashCode,每个不同的对象其哈希值都不相同,其实底层是对象的内存地址的32位的散列值,h >>> 16的意思是将hashcode右移16位,然后高位补0,然后再与(h = key.hashCode()) 异或运算得到最终的h值。
为什么是异或运算呢?
当然我们知道目的是为了让h的低16位更有散列性,但为什么是异或运算就更有散列性呢?而不是与运算或者或运算呢?这里我自己证明一下为什么异或就能够得到更好散列性。
先来看一下下面的这组运算
【与运算 1&0=0, 0&0=0, 0&1=0 都等于0 1&1=1 3次0,1次1】
【或运算 1&0=1, 1&1=1, 0&1=1 都等于1 0&0=0 3次1,1次0】
【异或运算 0&0=0, 1&1=0,而另外0&1=1, 1&0=1 2次1,2次0】
上面是将0110和0101分别进行与、或、异或三种运算得到不同的结果,我们主要来看计算的过程:
与运算:其中1&1=1,其他三种情况1&0=0, 0&0=0, 0&1=0 都等于0,可以看到与运算的结果更多趋向于0,这种散列效果就不好了,运算结果会比较集中在小的值
或运算:其中0&0=0,其他三种情况 1&0=1, 1&1=1, 0&1=1 都等于1,可以看到或运算的结果更多趋向于1,散列效果也不好,运算结果会比较集中在大的值
异或运算:其中0&0=0, 1&1=0,而另外0&1=1, 1&0=1 ,可以看到异或运算结果等于1和0的概率是一样的,这种运算结果出来当然就比较分散均匀了
总的来说,与运算的结果趋向于得到小的值,或运算的结果趋向于得到大的值,异或运算的结果大小值比较均匀分散,这就是我们想要的结果,这也解释了为什么要用异或运算,因为通过异或运算得到的h值会更加分散,进而 h & (length-1)得到的index也会更加分散,哈希冲突也就更少。
为什么使用 hash & (length - 1) 作为数组的寻址算法?
首先我们如果把数据存在一个数组中,我们会使用数组中的值hash % length取模操作,为每个值寻找存在数组中的位置,但是这种取模的操作性能不是很好,比起位运算差远了,后来发现当数组的容是2的n次方的时候hash & (length - 1) == hash % length,所以就使用hash & (length - 1) 来替代取模运算,这样操作效率高,而且数据均匀分布,hash碰撞少。
使用hash & (length - 1) 作为寻址算法也是jdk1.8的优化。
寻址算法的优化:使用与运算替代取模,提升性能。
那为什么要用数组值的hash值的高16与它的低16做异或呢?
首先我们的寻址算法优化了,是使用hash & (length - 1) ,假设我们不适用新的优化后的hash算法,我们就直接使用数组中的值的hashcode,不使用高16与低16做异或,因为n-1的值通常是很小的,n-1通常高16为都是0,那么这个hash的高16为和n-1做与运算,hash的高16位就不起作用了,就相当于与之与两个都是低16位的值做与预算,而我们的目的就是为了hash更加散列,很少甚至不起hash冲突。所以如果使用hash值的高16与低16做异或,让他的低16为同时保持了高低16为的特征,尽量避免了hash冲突。
HashMap的容量为什么建议是2的幂次方?
关键就在于把当前数据存放到哪一个桶中,这个算法就是取模运算。
假设:
length:HashMap的容量
hash:当前key的哈希值
取模运算为 hash % length
但是,在计算机中,直接取模运算的效率不如位运算(&),什么是位运算?就是对于二进制数据的按位运算,1和1才得1,其他都得0,比如:1011 & 1100 = 1000
sun公司的大牛们发现,当容量为2的n次方时,hash & (length - 1) == hash % length ,于是就在源码中做了优化,通过 hash & (length - 1) 来替代取模运算,而前提就是容量必须为2的n次方。这样做的好处在于:
1. 提高操作运算效率(位运算效率 > 取模运算效率)
2. 减少碰撞,数据均匀分布,提高HashMap查询效率
为什么可以减少碰撞?举个例子,现在两个hash分别是2和3,:
比如 length 为 9 的情况:3&(9-1)=0 2&(9-1)=0 ,都在0上,碰撞了;
比如 length 为 8 的情况:3&(8-1)=3 2&(8-1)=2 ,不同位置上,不碰撞;
为什么不采用AVL树或B树,B+树?
红黑树和AVL树都是最常用的平衡二叉搜索树。
但是,两者之间有些许不同:
AVL树更加严格平衡,因此可以提供更快的査找效果。因此,对于查找密集型任务使用AVL树没毛病。 但是对于插入密集型任务,红黑树要好一些。
通常,AVL树的旋转比红黑树的旋转更难实现和调试。
红黑树更通用,再添加删除来说表现较好,AVL虽能提升一些速度但是代价太大了。
而不用B/B+树的原因:
B和B+树主要用于数据存储在磁盘上的场景,比如数据库索引就是用B+树实现的。这两种数据结构的特点就是树比较矮胖,每个结点存放一个磁盘大小的数据,这样一次可以把一个磁盘的数据读入内存,减少磁盘转动的耗时,提高效率。而红黑树多用于内存中排序,也就是内部排序。
为什么树化阈值是8?为什么树退化为链表的阈值是6?
根据泊松分布。当我们计算的哈希冲突到了8次,概率就非常小了,可以看到当链表长度为8时候的概率为千万分之6,概率极低。所以取该值作为树化阈值。
相关文章:

HashMap源码阅读解惑
HashMap的hash函数(1.8) 首先1.7的是四次扰动,1.8做了优化。 简单的说就是对key做hashCode操作,然后将得到的32为散列值向右位移16位,再与hashCode做异或计算。实质上是把一个数的低16位与他的高16位做异或运算。 st…...

如何解决前端传递数据给后端时精度丢失问题
解决精度丢失 有时候我们在进行修改操作时,发现修改既不报错也不生效。我们进行排查后发现服务器端将数据返回给前端时没有出错,但是前端js将数据进行处理时却出错了,因为id是Long类型的,而js在处理后端返回给前端的Long类型数据…...
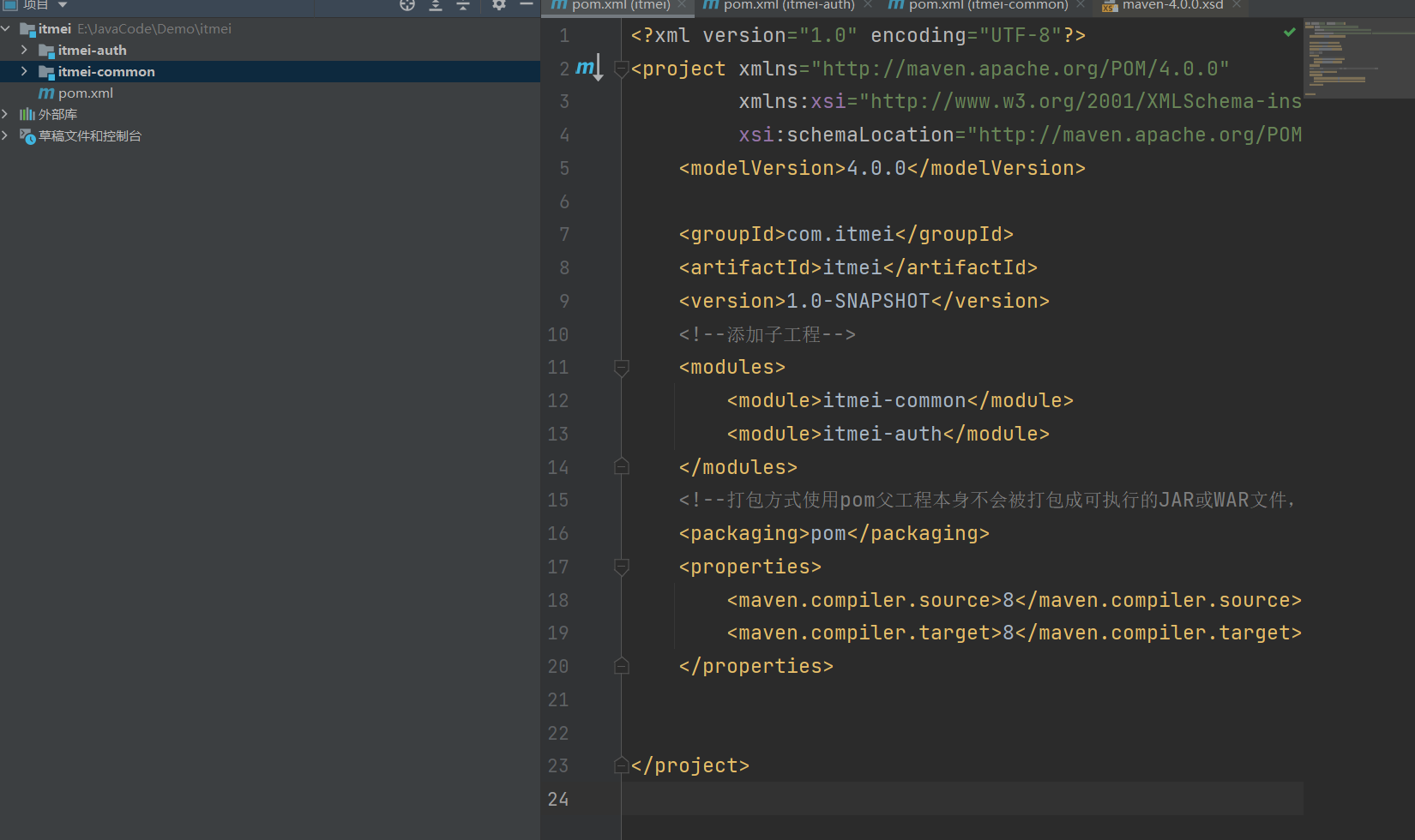
使用Maven创建父子工程
📚目录 创建父工程创建子模块创建子模块示例创建认证模块(auth) 结束 创建父工程 选择空项目: 设置:项目名称,组件名称,版本号等 创建完成后的工程 因为我们需要设置这个工程为父工程所以不需要src下的所有文件 在pom…...
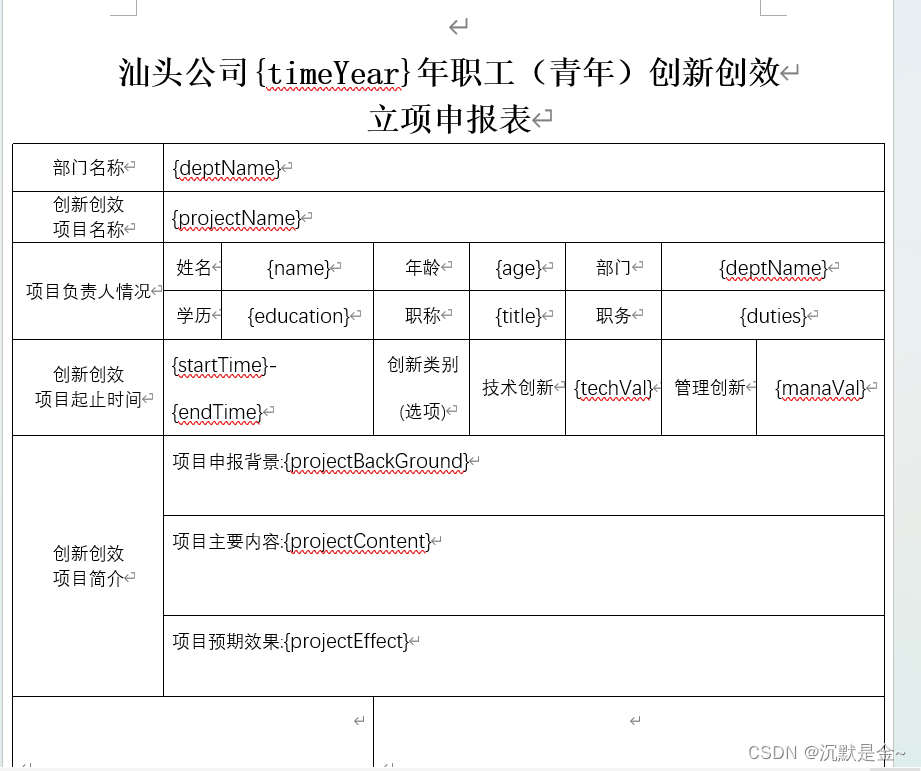
Vue+elementUI 导出word打印
import JSZipUtils from "jszip-utils"; import JSZip from "pizzip"; import Docxtemplater from "docxtemplater"; npm安装以上依赖 首先维护个word模板 导出方法 //导出wordskipOutWord(row) {var printData rowconst data JSON.parse(JS…...

数学建模-点评笔记 9月3日
1.摘要:关键方法和结论(精炼的语言)要说明,方法的合理性和意义也可以说明。 评委先通过摘要筛选(第一轮) 2.时间序列找异常值除了3西格玛还有针对时间序列更合适寻找的方法 3.模型的优缺点要写的详细一点…...
)
使用Spring来管理对象关系映射(ORM)
简介 对象关系映射(Object-Relational Mapping,简称ORM)是一种技术,用于在面向对象程序和关系型数据库之间进行数据的映射。Spring框架提供了强大的支持来简化和优化ORM开发过程。本文将介绍如何使用Spring来管理对象关系映射。 …...

【消息中间件】详解三大MQ:RabbitMQ、RocketMQ、Kafka
作者简介 前言 博主之前写过一个完整的MQ系列,包含RabbitMQ、RocketMQ、Kafka,从安装使用到底层机制、原理。专栏地址: https://blog.csdn.net/joker_zjn/category_12142400.html?spm1001.2014.3001.5482 本文是该系列的清单综述…...

算法:删除有序数组中的重复项---双指针[3]
1、题目: 对给定的有序数组 nums 删除重复元素,在删除重复元素之后,每个元素只出现一次,并返回新的长度,上述操作必须通过原地修改数组的方法,使用 O(1) 的空间复杂度完成。 2、分析特点: 题目…...

AR产业变革中的“关键先生”和“关键力量”
今年6月的WWDC大会上,苹果发布了头显产品Vision Pro,苹果CEO库克形容它: 开启了空间计算时代。 AR产业曾红极一时,但因为一些技术硬伤又减弱了声量,整个产业在起伏中前行。必须承认,这次苹果发布Vision P…...
通过 Blob 对二进制流文件下载实现文件保存下载
原理:前端将二进制文件做转换实现下载: 请求后端接口->接收后端返回的二进制流(通过二进制流(Blob)下载,把后端返回的二进制文件放在 Blob 里面)->再通过file-saver插件保存 页面上使用: <span click"downloadFil…...

微信小程序使用lime-echart踩坑记录
一、使用echarts包 微信小程序项目使用的是uni-app,插件是lime-echart,版本一开始安装的是lime-echart-0.7.9;在项目分包之后,为了避免主包过大,就将这个插件也一并搬到了分包中,在微信开发者工具中表现出…...
Unity 编辑器资源导入处理函数 OnPostprocessTexture :深入解析与实用案例
Unity 编辑器资源导入处理函数 OnPostprocessTexture 用法 点击封面跳转下载页面 简介 在Unity中,我们可以使用编辑器资源导入处理函数(OnPostprocessTexture)来自定义处理纹理资源的导入过程。这个函数是继承自AssetPostprocessor类的&…...
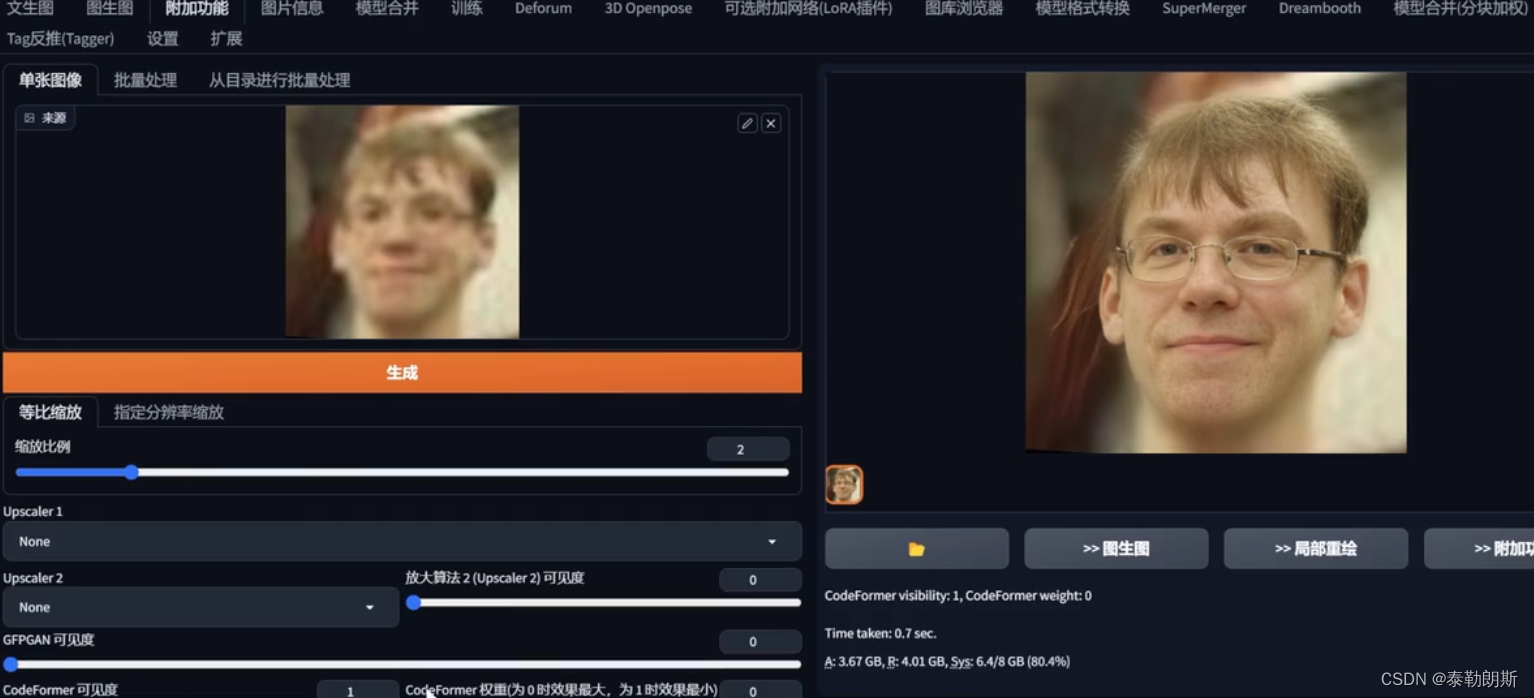
stable diffusion实践操作-宽高设置以及高清修复
系列文章目录 stable diffusion实践操作 文章目录 系列文章目录前言一、SD宽高怎么设置?1.1 宽高历史 二、高清修复1. 文生图中的高清修复1.按钮Hires.fix2.不同放大算法对比1.第一类2.第二类3.第三类4.第四类5.第五类6.第六类7.第七类8.第八类9.第九类10.第十类11…...

利用微调的deberta-v3-large来预测情感分类
前言: 昨天我们讲述了怎么利用emotion数据集进行deberta-v3-large大模型的微调,那今天我们就来输入一些数据来测试一下,看看模型的准确率,为了方便起见,我直接用测试集的前十条数据 代码: from transfor…...

opencv旋转图像
0 、使用旋转矩阵旋转 import cv2img cv2.imread(img.jpg, 1) (h, w) img.shape[:2] # 获取图像的宽和高# 定义旋转中心坐标 center (w / 2, h / 2)# 定义旋转角度 angle 90# 定义缩放比例 scale 1# 获得旋转矩阵 M cv2.getRotationMatrix2D(center, angle, scale)# 进行…...
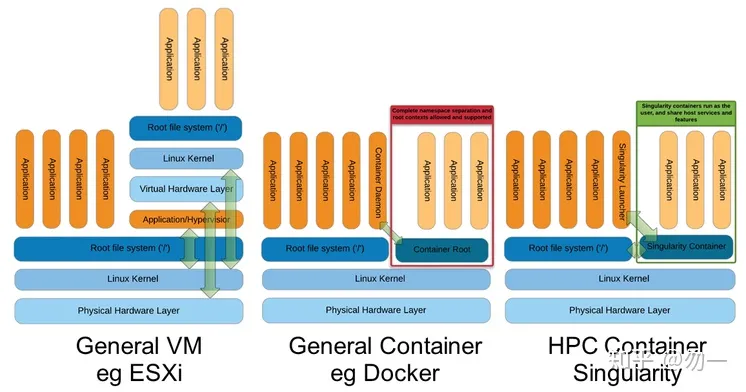
容器资料: Docker和Singularity
容器资料 Docker和Singularity Docker比较适合测试: 环境适配,每种环境对应一个容器。Docker需要host宿主机上运行Docker服务(root权限),隔离性很高,但会牺牲性能,对GPU环境支持不好(需要安装NVIDIAN公司的插件才能把GPU暴露给container) Sigularity可…...
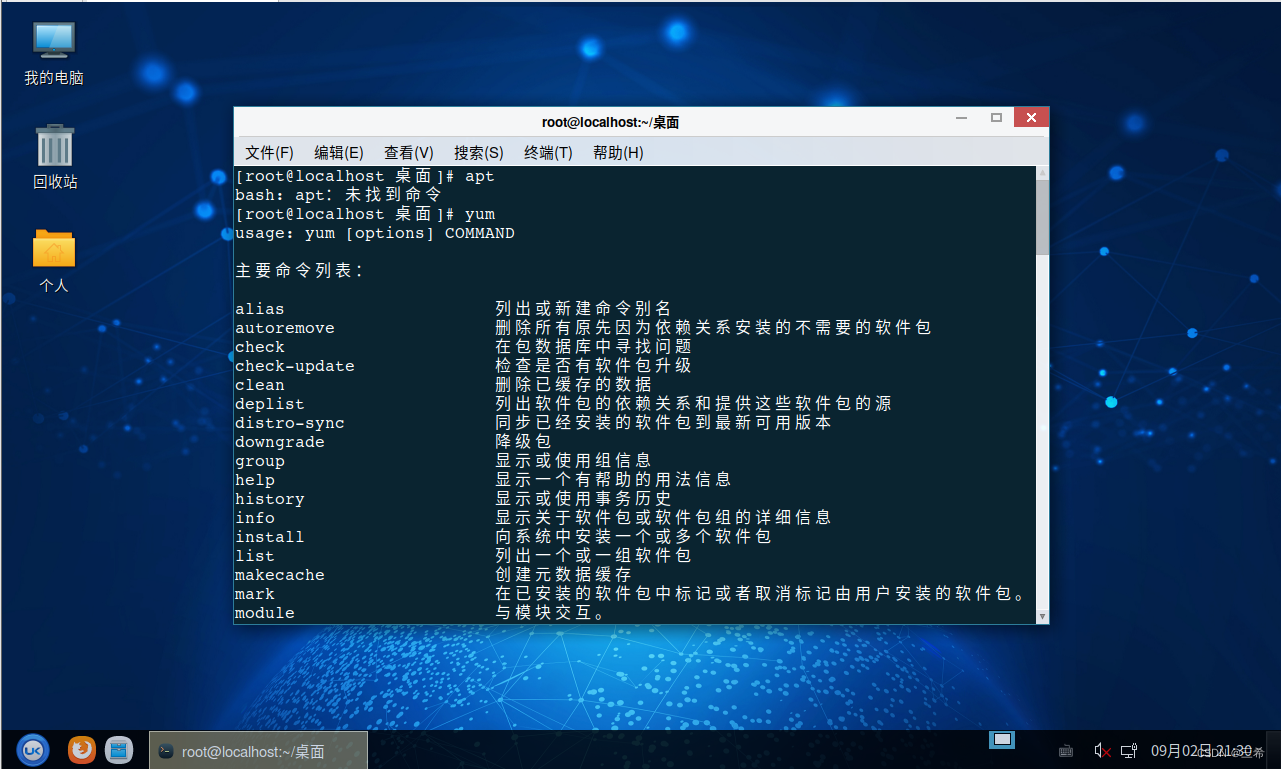
如何确认linux的包管理器是yum还是apt,确认之后安装其他程序的时候就需要注意安装命令
打开终端 输入apt,下图中提示未找到命令,则基本上包管理工具就是用yum的 输入yum,我们看到有打印信息,则说明包管理工具是yum的,离线安装命令使用rpm...

数据分享|R语言分析上海空气质量指数数据:kmean聚类、层次聚类、时间序列分析:arima模型、指数平滑法...
全文链接:http://tecdat.cn/?p30131 最近我们被客户要求撰写关于上海空气质量指数的研究报告。本文向大家介绍R语言对上海PM2.5等空气质量数据(查看文末了解数据免费获取方式)间的相关分析和预测分析,主要内容包括其使用实例&…...
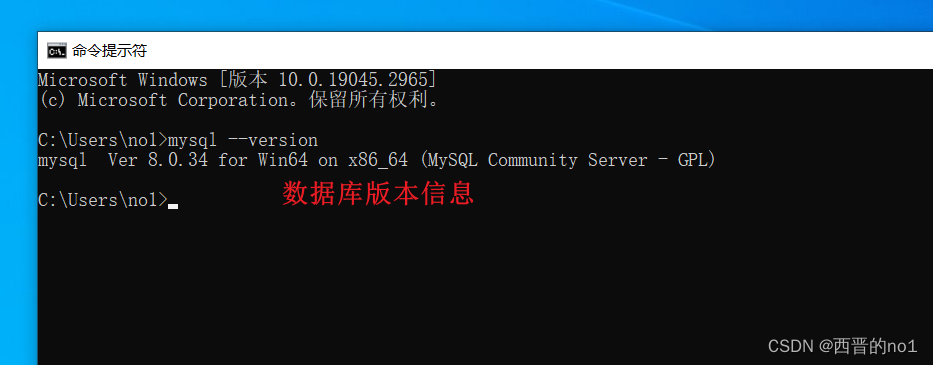
MySQL 8.0.34安装教程
一、下载MySQL 1.官网下载 MySQL官网下载地址: MySQL :: MySQL Downloads ,选择下载社区版(平时项目开发足够了) 2.点击下载MySQL Installer for Windows 3.选择版本8.0.34,并根据自己需求,选择下载全社区安…...
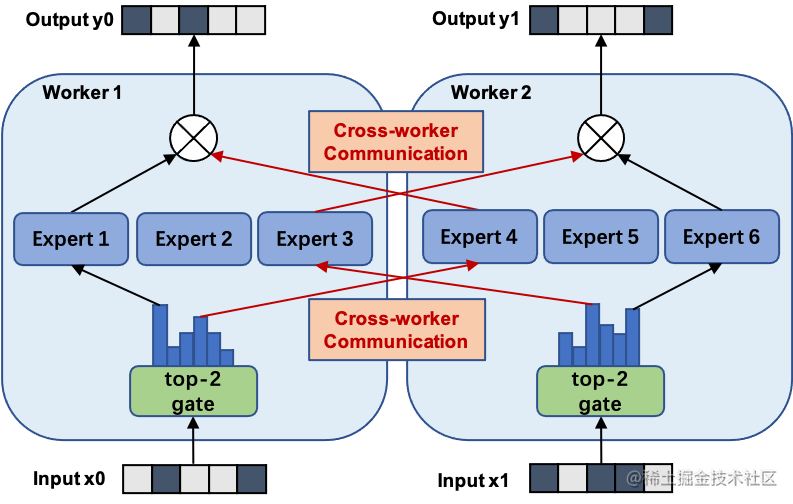
用通俗易懂的方式讲解大模型分布式训练并行技术:概述
近年来,随着Transformer、MOE架构的提出,使得深度学习模型轻松突破上万亿规模参数,传统的单机单卡模式已经无法满足超大模型进行训练的要求。因此,我们需要基于单机多卡、甚至是多机多卡进行分布式大模型的训练。 而利用AI集群&a…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
