数学建模:模糊综合评价分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
数学建模:模糊综合评价分析
文章目录
- 数学建模:模糊综合评价分析
- 综合评价分析
- 常用评价方法
- 一级模糊综合评价
- 综合代码
- 多级模糊综合评价
- 总结
综合评价分析
构成综合评价类问题的五个要素:
- 被评价对象
- 评价指标
- 权重系数
- 综合评价模型
- 评价者
综合评价的一般步骤:
- 确定综合评价的目的(分类?排序?实现程度)
- 建立评价指标体系
- 对指标数据进行预处理:一致化和无量纲化处理
- 确定各个指标的权重
- 求综合评价值
常用评价方法



一级模糊综合评价
- 评价对象为 X X X ,其具有评价指标集: U = { u 1 , u 2 , . . . u m } U = \left \{u_1,u_2,...u_m \right \} U={u1,u2,...um}, 具有评价等级集:V = { v 1 , v 2 , . . . v n } \left \{v_1,v_2 , ... v_n \right\} {v1,v2,...vn}
- m m m 表示指标(因素) n n n 表示评语的总个数。
- 对 U 中每一指标根据评判集中的等级指标进行模糊评判,得到相对偏差模糊矩阵 R R R , 其中 i , j i,j i,j 表示第 i i i 个指标处于 j j j 评语的隶属度是 R i j R_{ij} Rij
R = [ r 11 , r 12 , ⋯ , r 1 n r 21 , r 22 , ⋯ , r 2 n r m 1 , r m 2 , ⋯ , r m n ] R=\begin{bmatrix}r_{11},r_{12},\cdots,r_{1n}\\r_{21},r_{22},\cdots,r_{2n}\\r_{m1},r_{m2},\cdots,r_{mn}\end{bmatrix} R= r11,r12,⋯,r1nr21,r22,⋯,r2nrm1,rm2,⋯,rmn
- 自此 { U , V , R } \left \{ U,V,R \right \} {U,V,R} 构成一个模糊综合评价模型,然后确定各指标的权系数向量,记为 : A A A
A = { a 1 , a 2 , ⋯ , a n } A=\{a_{1},a_{2},\cdots,a_{n}\} A={a1,a2,⋯,an}
- 利用矩阵的模糊乘法得到综合模糊评价结果,合成评价结果 B B B :
运算为模糊乘法,逻辑乘∧(取最小)和逻辑加∨(取最大)
B = A ⋅ R B = A\cdot R B=A⋅R
- 归一化(标准化)后,得到:
B = { b 1 , b 2 , ⋯ , b m } B=\{b_{1},b_{2},\cdots,b_{m}\} B={b1,b2,⋯,bm}
- 因此便可以根据 B B B 来判断评价结果。
如何得到相对偏差模糊矩阵 R R R ?
-
相对偏差评价法:
-
虚拟化理想方案 u u u
u = ( u 1 , u 2 , ⋯ , u n ) u i = { max j { a i j } , a i j 为效益型指标 min j { a i j } , a i j 为成本型指标 u{=}(u_1,u_2,\cdots,u_n)\\\\{u_i=\begin{cases}\max_j\left\{a_{ij}\right\},&a_{ij}\text{为效益型指标}\\\min_j\left\{a_{ij}\right\},&a_{ij}\text{为成本型指标}&\end{cases}} u=(u1,u2,⋯,un)ui={maxj{aij},minj{aij},aij为效益型指标aij为成本型指标
-
建立相对偏差模糊矩阵 R R R :
R = ( r 11 r 12 ⋯ r 1 n r 21 r 22 ⋯ r 2 n ⋮ ⋮ ⋱ ⋮ r m 1 r m 2 ⋯ r m n ) r i j = ∣ a i j − u i ∣ max j { a i j } − min j { a i j } \begin{gathered}\text{R} =\left(\begin{array}{cccc}r_{11}&r_{12}&\cdots&r_{1n}\\r_{21}&r_{22}&\cdots&r_{2n}\\\vdots&\vdots&\ddots&\vdots\\\\r_{m1}&r_{m2}&\cdots&r_{mn}\end{array}\right) \\\\\boldsymbol{r_{ij}} =\frac{\left|a_{ij}-u_i\right|}{\max_j\left\{a_{ij}\right\}-\min_j\left\{a_{ij}\right\}} \end{gathered} R= r11r21⋮rm1r12r22⋮rm2⋯⋯⋱⋯r1nr2n⋮rmn rij=maxj{aij}−minj{aij}∣aij−ui∣
-
-
相对优属度评价法:
-
使用如下公式来计算相对偏差模糊矩阵 R R R:
r i j = { a i j / max j { a i j } , a i j 为效益型 min j { a i j } / a i j , a i j 为成本型 min j ∣ a i j − α j ∣ / a i j − α j ∣ , a i j 为固定型 \begin{aligned}r_{ij}&=\begin{cases}a_{ij}\Big/\max_j\left\{a_{ij}\right\},a_{ij}\text{为效益型}\\\min_j\left\{a_{ij}\right\}\Big/a_{ij},a_{ij}\text{为成本型}\\\min_j\left|a_{ij}-\alpha_j\right|\Big/a_{ij}-\alpha_j\Big|,a_{ij}\text{为固定型}&\end{cases}\end{aligned} rij=⎩ ⎨ ⎧aij/maxj{aij},aij为效益型minj{aij}/aij,aij为成本型minj∣aij−αj∣/aij−αj ,aij为固定型
-
如何得到指标权系数向量 A A A ?
变异系数法。
数学建模:变异系数法 | HugeYlh
- 得到第 i i i 项指标的均值与方差
x i ‾ = 1 n ∑ j = 1 n a i j , s i 2 = 1 n − 1 ∑ j = 1 n ( a i j − x i ‾ ) 2 ν i = s i / ∣ x i ‾ ∣ \overline{x_i}=\frac1n\sum_{j=1}^na_{ij},s_i^2=\frac1{n-1}\sum_{j=1}^n\left(a_{ij}-\overline{x_i}\right)^2 \\\\\boldsymbol{\nu_{i}}=\boldsymbol{s_{i}}/\left|\overline{\boldsymbol{x_{i}}}\right|\boldsymbol{} xi=n1j=1∑naij,si2=n−11j=1∑n(aij−xi)2νi=si/∣xi∣
- 得到权重值 a i a_i ai
a i = ν i / ∑ ν i a_i=\nu_i/\sum\nu_i ai=νi/∑νi
熵权法
数学建模:熵权法 | HugeYlh
- 计算每一个指标所占全部指标的比例,得到变异值矩阵
p i j = Y y ¨ ∑ i = 1 m Y i j , i = 1 , ⋯ , m , j = 1 , ⋯ , n p_{ij}=\frac{Y_{\ddot{y}}}{\sum_{i=1}^mY_{ij}},i=1,\cdots,m,j=1,\cdots,n pij=∑i=1mYijYy¨,i=1,⋯,m,j=1,⋯,n
-
计算信息熵
E j = − ln ( m ) − 1 ∑ i = 1 m p i j ln p i j E_j=-\ln(m)^{-1}\sum_{i=1}^mp_{ij}\ln p_{ij} Ej=−ln(m)−1i=1∑mpijlnpij
-
获取各个指标的权重
综合代码
- 使用相对偏差评价法求得模糊矩阵 R R R :
clc;clear;
% 5行 7列 表示5个评价对象,6项指标
X=[1000 120 5000 1 50 1.5 1
700 60 4000 2 40 2 2
900 60 7000 1 70 1 4
800 70 8000 1.5 40 0.5 6
800 80 4000 2 30 2 5];
% 其中第一列与最后一列指标为效益性(越大越好),其他指标为成本型(越小越好)
[m,n]=size(X);%% 计算相对偏差模糊矩阵R
maxA=max(X);
minA=min(X);
G=maxA-min(X);%最大值减去最小值
A1=max(X(:,1));%A1为效益型
A2=min(X(:,2:n-1));%A2~A6为成本型
A3=max(X(:,7));%A7为效益型
u=[A1,A2,A3]; %得到u然后带入到求 每个r_{ij} 的公式
%%
R = X;
R = (abs(X-repmat(u,m,1)))./G;%% 利用变异系数计算权向量A
x=mean(X);
s=std(X);
v=s./x;
vsum=sum(v);
A = v./vsum;%% B为m个评价结果
B=R*(A');
- 使用相对优属度来求得模糊矩阵 R R R
R i j = a i j m a x j ( a i j ) R_{ij} = \frac {a_{ij}}{max_{j}(a_{ij})} Rij=maxj(aij)aij
%%
clc;clear;close all;
A=[58 38 14 8 57 10
50 45 11 9 52 12
42 47 8 12 50 15
45 42 12 15 46 16
47 44 13 10 49 13];
[m,n]=size(A);
h=max(A);%最大值
H=repmat(h,m,1);
Mij=A./H;% 得到模糊关系矩阵Mij 相对优属度 %% 熵权法
% 得到变异值矩阵
Qij = Mij./repmat(sum(Mij),m,1);% 计算各指标的信息熵
for j=1:n% 计算每个指标的信息熵fj(j)=-1/log(m)*sum(Qij(:,j).*log(Qij(:,j)));
end% 计算各指标权重
v=(1-fj)./sum((1-fj));B=Qij*v';%最终评价结果
disp(B)%显示结果
多级模糊综合评价
评价模型:
C = A B = A ( A 1 R 1 A 2 R 2 ⋯ A n R n ) = A ( B 1 B 2 ⋯ B n ) C=A\text{B}=A\left(\begin{array}{c}A_1R_1\\A_2R_2\\\cdots\\A_nR_n\end{array}\right)=A\left(\begin{array}{c}B_1\\B_2\\\cdots\\B_n\end{array}\right) C=AB=A A1R1A2R2⋯AnRn =A B1B2⋯Bn
即计算出各个二级指标的模糊综合评价的归一化后的评价结果 B B B 后,然后分别进行一级指标的模糊综合评价,并且得到结果: C C C
总结
- 灰色关联分析法、相对偏差法和相对优属度法对同一问题的评价、排序结果不尽相同.
- 当各指标在评价体系重要性相当时,用变异系数法确定指标权重,可提高上述方法排序的分辨率;
- 当各指标在评价体系重要性差异较大时,可考虑用层次分析法确定指标权重;
- 在实际中, 对于评价类问题,应同时应用上述几种方法进行综合评价,以提高评价的可靠性。
31 老哥带你学数模:模糊综合评价算法.pdf
相关文章:

数学建模:模糊综合评价分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:模糊综合评价分析 文章目录 数学建模:模糊综合评价分析综合评价分析常用评价方法一级模糊综合评价综合代码 多级模糊综合评价总结 综合评价分析 构成综合评价类问题的五个…...

智能小车—PWM方式实现小车调速和转向
目录 1. 让小车动起来 2. 串口控制小车方向 3. 如何进行小车PWM调速 4. PWM方式实现小车转向 1. 让小车动起来 电机模块开发 L9110s概述 接通VCC,GND 模块电源指示灯亮, 以下资料来源官方,具体根据实际调试 IA1输入高电平,…...

Getx其他高级API
// 给出当前页面的args。 Get.arguments//给出以前的路由名称 Get.previousRoute// 给出要访问的原始路由,例如,rawRoute.isFirst() Get.rawRoute// 允许从GetObserver访问Rounting API。 Get.routing// 检查 snackbar 是否打开 Get.isSnackbarOpen// 检…...

npm/yarn link 测试包时报错 Warning: Invalid hook call. Hooks can only be called ...
使用 dumi 开发 React 组件库时,为避免每次修改都发布到 npm,需要在本地的测试项目中使用 npm link 为组件库建立软连接,方便本地调试。 结果在本地测试项目使用 $ npm link 组件库 后,使用内部组件确报错: react.dev…...
「网页开发|前端开发|Vue」06 公共组件与嵌套路由:让每一个页面都平等地拥有导航栏
本文主要介绍在多个页面存在相同部分时,如何提取公共组件然后在多个页面中导入组件重复使用来减少重复代码。在这基础上介绍了通过嵌套路由的方式来避免页面较多或公共部分较多的情况下,避免不断手动导入公共组件的麻烦,并且加快页面跳转的速…...

leetcode687. 最长同值路径(java)
最长同值路径 题目描述DFS 深度遍历代码演示 题目描述 难度 - 中等 LC - 687. 最长同值路径 给定一个二叉树的 root ,返回 最长的路径的长度 ,这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。 两个节点之间的路径长度 由它们之…...
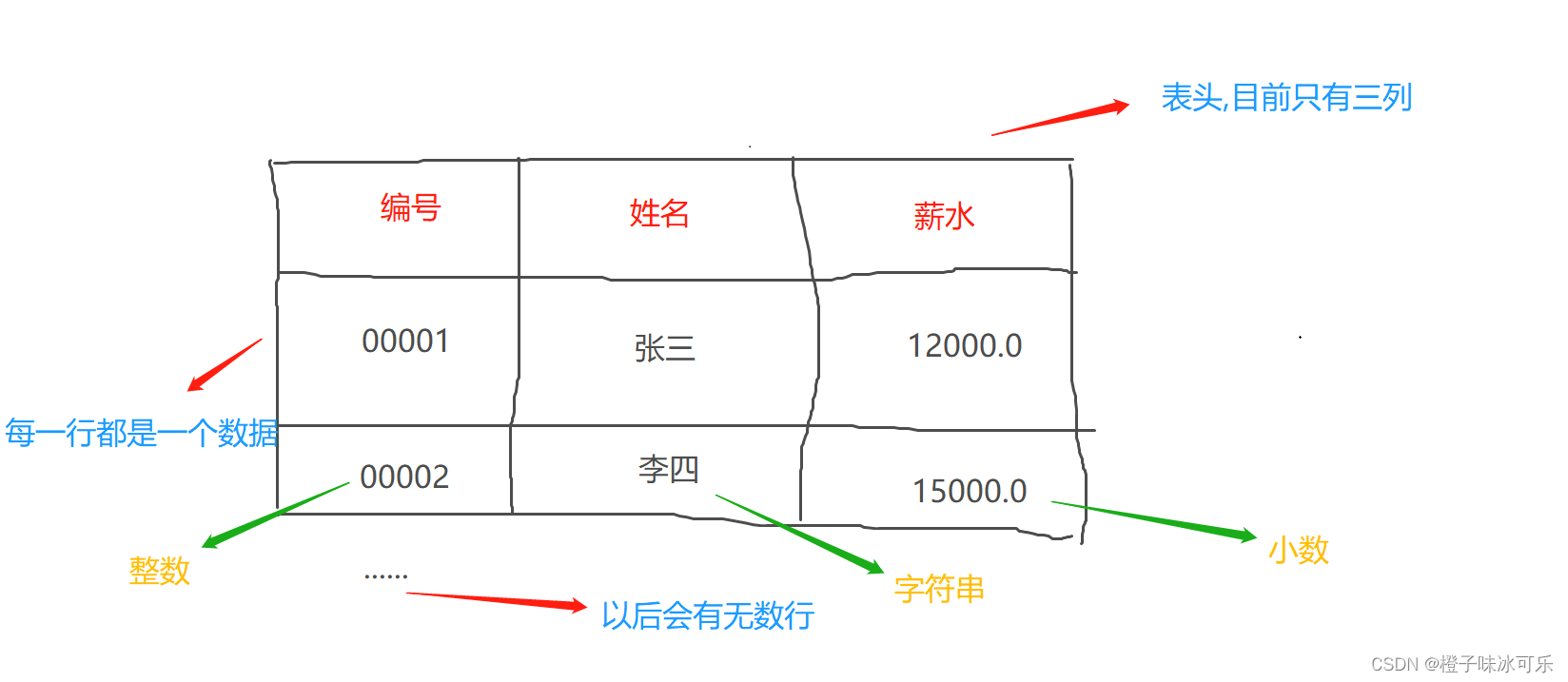
MySQL的常用术语
目录 1.关系 2.元组 3.属性 MySQL从小白到总裁完整教程目录:https://blog.csdn.net/weixin_67859959/article/details/129334507?spm1001.2014.3001.5502 1.关系 前面的博客有说到,MySQL是一款关系型数据库管理软件,一个关系就是 一张二维表(表) 我想大家都知道表格怎么…...
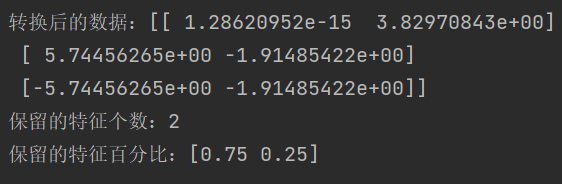
机器学习的特征工程
字典特征提取 def dict_demo():"""字典特征提取:return:"""data [{city: 北京, temperature: 100}, {city: 上海, temperature: 60}, {city: 深圳, temperature: 30}]# data [{city:[北京,上海,深圳]},{temperature:["100","6…...
python3 修改nacos的yaml配置
一、安装nacos库 pip install nacos-sdk-python 二、代码如下 import nacos import yaml# 连接地址 NACOS_SERVER_ADDRESSES "192.168.xx.xx" NACOS_SERVER_PORT 替换为你的端口号,如8848# 命名空间 NACOS_NAMESPACE "your_namespace"# 账…...

YOLOv8 : 数据组织
1. 数据源 首先YOLOv8是支持目标分类、检测和目标分割。当前以应用最为广泛的目标检测为例,简单说明数据相关的信息。 一般情况下,建议将数据划分成images和labels,其中images存储图像,labels存储标签文件(YOLO格式)。如果是VOC数…...

golang如何生成zip压缩文件
在Golang中,您可以使用标准库中的compress/zip包来生成ZIP压缩文件。下面是一个简单的示例代码,演示如何使用该包来创建一个ZIP文件并将文件添加到其中: package main import ( "archive/zip" "bytes" "fmt&qu…...

AntDesign技术指南:构建优雅的前端界面
引言 AntDesign是一款优秀的前端UI组件库,它提供了丰富的组件和功能,帮助我们快速构建漂亮、易用的前端界面。本篇博客将详细介绍AntDesign的使用方法和技巧,并展示完整的代码示例。无论你是初学者还是有经验的开发者,本篇博客都…...

机器人任务挖掘与智能超级自动化技术解析
本文为上海财经大学教授、安徽财经大学学术副校长何贤杰出席“会计科技Acctech应对不确定性挑战”高峰论坛时的演讲内容整理。何贤杰详细介绍了机器人任务挖掘与智能超级自动化技术的发展背景、关键技术和应用场景。 从本质来说,会计是非常适合智能化、自动化的。会…...

C#通过ModbusTcp协议读写西门子PLC中的浮点数
一、Modbus TCP通信概述 MODBUS/TCP是简单的、中立厂商的用于管理和控制自动化设备的MODBUS系列通讯协议的派生产品,显而易见,它覆盖了使用TCP/IP协议的“Intranet”和“Internet”环境中MODBUS报文的用途。协议的最通用用途是为诸如PLC,I/…...

19-springcloud(中)
一 服务注册发现 1 什么是服务治理 为什么需要服务治理 在没有进行服务治理前,服务之间的通信是通过服务间直接相互调用来实现的。 过程: 武当派直接调用峨眉派和华山派,同样,华山派直接调用武当派和峨眉派。如果系统不复杂,这样…...
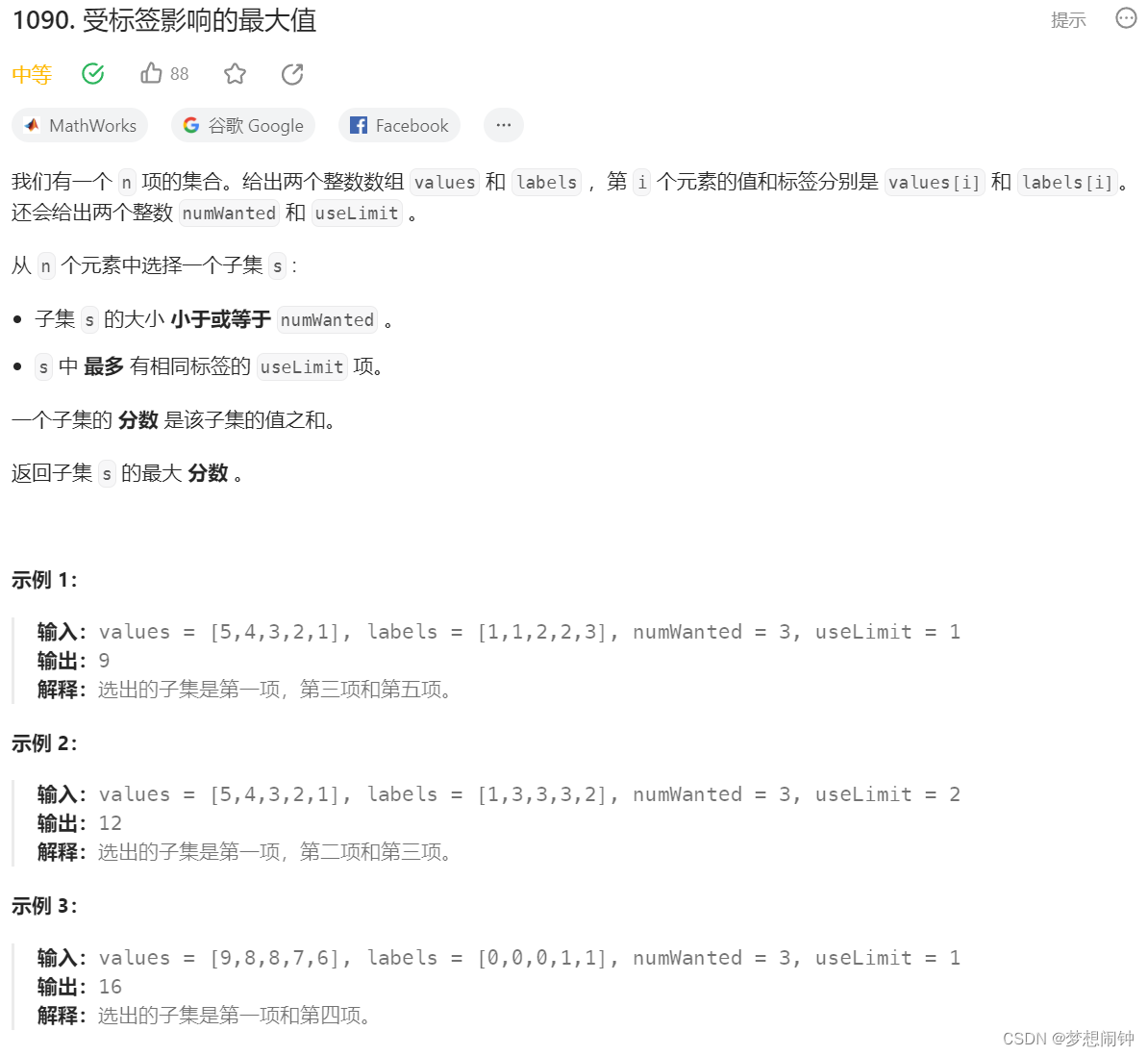
Leetcode1090. 受标签影响的最大值
思路:根据值从大到小排序,然后在加的时候判断是否达到标签上限即可,一开始想用字典做,但是题目说是集合却连续出现两个8,因此使用元组SortedList进行解决 class Solution:def largestValsFromLabels(self, values: li…...
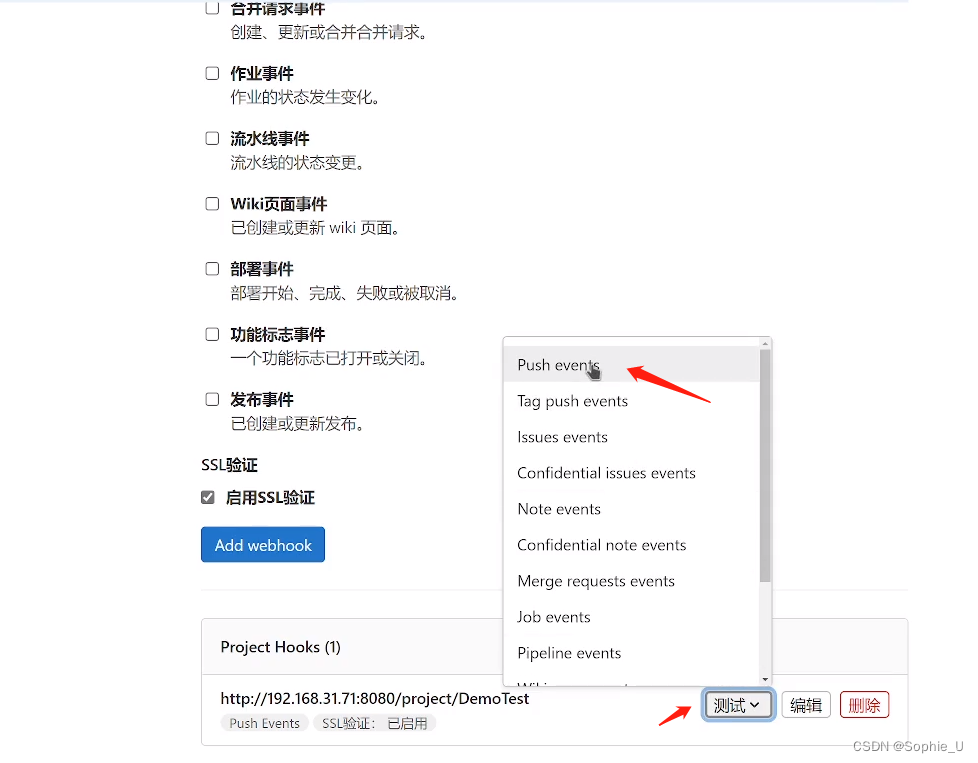
第七章:敏捷开发工具方法-part2-CI/CD工具介绍
文章目录 前言一、CI-持续集成1.1 安装部署gitlab 二、gitlab CI配置三、jenkins实现CI / CD3.1 安装jenkins3.2 配置CI3.3 配置CD3.4 其他构建方式1、定时构建2、指定参数构建3、webhook自动根据git事件进行构建 前言 什么是CI/Cd? CI-Continuous integration&…...
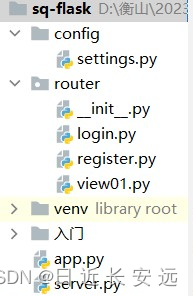
【自学开发之旅】Flask-回顾--对象拆分-蓝图(二)
url-统一资源定位符-不同的url对应不同的资源 作为服务端,url和视图函数的映射关系就是路由。 定义传递参数的方式: 1.创建动态url app.route("/login2/<username>/<passwd>") def login2(username, passwd):if username "…...

自动驾驶中间件
自动驾驶中间件 1. 什么是中间件2. 中间件的分类3. 自动驾驶为什么需要中间件4. 通信中间件 Reference: 自动驾驶中间件:量产落地的关键技术通俗易懂的告诉你什么是中间件 对于初入自动驾驶行业的人来说,各色各样的新型传感器、线控系统、芯…...
移植javacpp)
鲲鹏920(ARM64)移植javacpp
JavaCPP JavaCPP 使得Java 应用可以在高效的访问本地C++方法,JavaCPP底层使用了JNI技术,可以广泛的用在Java SE应用中(也包括安卓),以下两个特性是JavaCPP的关键,稍后咱们会用到: 提供一些注解,将Java代码映射为C++代码提供一个jar,用java -jar命令可以将C++代码转为…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
