【理解线性代数】(四)线性运算的推广与矩阵基础
1. 数值加法和乘法
数值加法与乘法,是小学数学课程中的基本数学运算。例如:
加法:1+1=2
乘法:2*2=4
在这个知识层次下,运算的基本单位是数字。
2. 从数值到向量
数值加法,可以看作一维空间中的向量加法,即:
加法:(1) + (1) = (2)
数值乘法,可以看作一维空间中的向量乘法,即:
乘法:(2) * (2) = 2 * 2 * cos(0) = 4
通过将数值推广成一维向量,实现了数值和向量概念的统一。在这个知识层次下,向量是运算的基本单位。
3. 向量到矩阵
向量加法和乘法,总是两两进行运算,这种运算比较简单。
现实应用中,往往需要对很多向量组成的向量集合进行批量运算,向量批量运算有何规律?为了研究向量的批量运算,需要将一个向量集合视为一个整体,这个整体看起来是矩形的数字阵列,所以叫做 矩阵。例如下图是一个矩阵,此矩阵由 (a, b, c) 和 (d, e, f) 两个三维向量组成:
( a b c d e f ) \begin{pmatrix} a & b & c\\ d & e & f \end{pmatrix} (adbecf)
矩阵的行数表示向量个数,矩阵的列数表示向量的维度。
目前,矩阵仅仅表示多个向量的组合,没有其他任何含义,不需要想得太复杂。
下面将根据我们自己的理解,对矩阵运算规则进行推导,然后再和教科书上的运算规则进行比对,从而验证我们的理论。
3.1 矩阵加法
矩阵加法含义很简单,就是一组向量加上另外一组向量,对应位置的向量相加即可。因为向量相加,必须在两个向量之间进行,所以矩阵相加,两个相加的矩阵包含的向量个数必须相等,否则会因为缺少向量而无法进行。
可以正确进行的矩阵加法如下:
( a 1 b 1 c 1 d 1 e 1 f 1 ) + ( a 2 b 2 c 2 d 2 e 2 f 2 ) = ( a 1 + a 2 b 1 + b 2 c 1 + c 2 d 1 + d 2 e 1 + e 2 f 1 + f 2 ) \begin{pmatrix} a1 & b1 & c1\\ d1 & e1 & f1 \end{pmatrix} + \begin{pmatrix} a2 & b2 & c2\\ d2 & e2 & f2 \end{pmatrix} = \begin{pmatrix} a1+a2 & b1+b2 & c1+c2\\ d1+d2 & e1+e2 & f1+f2 \end{pmatrix} (a1d1b1e1c1f1)+(a2d2b2e2c2f2)=(a1+a2d1+d2b1+b2e1+e2c1+c2f1+f2)
无法进行的矩阵加法如下:
( a 1 b 1 c 1 d 1 e 1 f 1 ) + ( a 2 b 2 c 2 ) = 非法 \begin{pmatrix} a1 & b1 & c1\\ d1 & e1 & f1 \end{pmatrix} + \begin{pmatrix} a2 & b2 & c2 \end{pmatrix} = 非法 (a1d1b1e1c1f1)+(a2b2c2)=非法
3.2 矩阵乘法
下面从简单向复杂推导矩阵乘法运算规则。
3.2.1 1行3列矩阵 * 1行3列矩阵
设矩阵A:
A = ( a 1 b 1 c 1 ) A= \begin{pmatrix} a1 & b1 & c1 \end{pmatrix} A=(a1b1c1)
和矩阵B
B = ( a 2 b 2 c 2 ) B= \begin{pmatrix} a2 & b2 & c2 \end{pmatrix} B=(a2b2c2)
进行乘法运算,因为只有两个向量,可以尝试将这两个向量进行点乘运算,即:
A ∗ B = a 1 a 2 + b 1 b 2 + c 1 c 2 = ( a 1 a 2 + b 1 b 2 + c 1 c 2 ) A * B = a1a2 + b1b2 + c1c2 = (a1a2 + b1b2 + c1c2) A∗B=a1a2+b1b2+c1c2=(a1a2+b1b2+c1c2)
结果是一个数值,也可以看作是一个一维向量。
分析:
矩阵A包含1个三维向量,矩阵B包含1个三维向量,矩阵B可以代表三维空间中的一个一维空间,所以A中的所有向量投影到B,最终的结果变成了一个一维向量,符合我们对向量点乘及矩阵的理解。
3.2.2 2行3列矩阵 * 1行3列矩阵
增加矩阵A的行数,设矩阵A:
A = ( a 1 b 1 c 1 d 1 e 1 f 1 ) A= \begin{pmatrix} a1 & b1 & c1 \\ d1 & e1 & f1 \end{pmatrix} A=(a1d1b1e1c1f1)
和矩阵B
B = ( a 2 b 2 c 2 ) B= \begin{pmatrix} a2 & b2 & c2 \end{pmatrix} B=(a2b2c2)
进行乘法运算,尝试分别进行点乘运算,即:
A ∗ B = ( a 1 a 2 + b 1 b 2 + c 1 c 2 d 1 a 2 + b 1 b 2 + c 1 c 2 ) A * B = \begin{pmatrix} a1a2 + b1b2 + c1c2 \\ d1a2 + b1b2 + c1c2 \end{pmatrix} A∗B=(a1a2+b1b2+c1c2d1a2+b1b2+c1c2)
结果矩阵是一个2行1列的矩阵。
分析:
矩阵A包含2个三维向量,矩阵B包含1个三维向量,矩阵B可以代表三维空间中的一个一维空间,所以A中的所有向量投影到B,最终的结果变成了2个一维向量,符合我们对向量点乘及矩阵的理解。
3.2.3 2行3列矩阵 * 2行3列矩阵
设矩阵A:
A = ( a 1 b 1 c 1 d 1 e 1 f 1 ) A= \begin{pmatrix} a1 & b1 & c1 \\ d1 & e1 & f1 \end{pmatrix} A=(a1d1b1e1c1f1)
和矩阵B
B = ( a 2 b 2 c 2 d 2 e 2 f 2 ) B= \begin{pmatrix} a2 & b2 & c2 \\ d2 & e2 & f2 \end{pmatrix} B=(a2d2b2e2c2f2)
进行乘法运算,尝试分别进行点乘运算,即:
A ∗ B = ( a 1 a 2 + b 1 b 2 + c 1 c 2 a 1 d 2 + b 1 e 2 + c 1 f 2 d 1 a 2 + e 1 b 2 + f 1 c 2 d 1 d 2 + e 1 e 2 + f 1 f 2 ) A * B = \begin{pmatrix} a1a2 + b1b2 + c1c2 & a1d2+b1e2+c1f2\\ d1a2 + e1b2 + f1c2 & d1d2+e1e2+f1f2 \end{pmatrix} A∗B=(a1a2+b1b2+c1c2d1a2+e1b2+f1c2a1d2+b1e2+c1f2d1d2+e1e2+f1f2)
结果矩阵是一个2行2列的矩阵。
分析:
矩阵A包含2个二维向量,矩阵B包含2个三维向量,矩阵B可以代表三维空间中的一个二维平面空间(两条线组成一个面),所以A中的所有向量投影到B,最终的结果变成了2个二维向量,符合我们对向量点乘及矩阵的理解。
这个矩阵乘法稍微有些复杂,但有计算过程中有一个量没变,那就是矩阵A中向量的个数等于变换结果矩阵中向量的个数,即矩阵A的行数和变换结果矩阵的行数相等。在行数相等不变的情况下,只能将向
量点乘的结果按列依次向后摆放,最终,结果矩阵的列数,和矩阵B的行数相同。
3.2.4 矩阵不能相乘的情况
如果两个矩阵列数不同,也就是维度不同,还能相乘吗?
不能,因为向量点乘要求两个向量具有相同的维度,如果两个矩阵列数不同,矩阵中的向量互相无法进行点乘。不同维度的向量,坐标个数不一样,无法做乘法。
所以,两个矩阵相乘,必须乘号两边的矩阵有相同的维度。
3.2.5 推广
以
A ∗ B = C A * B = C A∗B=C
为例。
只要矩阵A和矩阵B的列数相同,不管矩阵A、矩阵B各自有多少行,都可以进行相乘。并且有:
- 结果矩阵C包含的向量个数和A中的向量个数相同,投影过程是一个线性变换,向量个数不会增加也不会减少,故投影前后向量个数不变。
- 结果矩阵C的向量维度和矩阵B的维度相同,因为矩阵C包含的向量,是矩阵A向矩阵B的投影,所以它们全部位于矩阵B所代表的空间中,所以C和B的维度必然相同。
3.2.6 验证复杂矩阵相乘:2行3列矩阵 * 3行3列矩阵
设矩阵A:
A = ( a 1 b 1 c 1 d 1 e 1 f 1 ) A= \begin{pmatrix} a1 & b1 & c1 \\ d1 & e1 & f1 \end{pmatrix} A=(a1d1b1e1c1f1)
和矩阵B
B = ( a 2 b 2 c 2 d 2 e 2 f 2 g 2 h 2 i 2 ) B= \begin{pmatrix} a2 & b2 & c2 \\ d2 & e2 & f2 \\ g2 & h2 & i2 \end{pmatrix} B= a2d2g2b2e2h2c2f2i2
进行乘法运算,结果为:
A ∗ B = ( a 1 a 2 + b 1 b 2 + c 1 c 2 a 1 d 2 + b 1 e 2 + c 1 f 2 a 1 g 2 + b 1 h 2 + c 1 i 2 d 1 a 2 + e 1 b 2 + f 1 c 2 d 1 d 2 + e 1 e 2 + f 1 f 2 d 1 g 2 + e 1 h 2 + f 1 i 2 ) A * B = \begin{pmatrix} a1a2 + b1b2 + c1c2 & a1d2+b1e2+c1f2 & a1g2+b1h2+c1i2\\ d1a2 + e1b2 + f1c2 & d1d2+e1e2+f1f2 & d1g2+e1h2+f1i2 \end{pmatrix} A∗B=(a1a2+b1b2+c1c2d1a2+e1b2+f1c2a1d2+b1e2+c1f2d1d2+e1e2+f1f2a1g2+b1h2+c1i2d1g2+e1h2+f1i2)
结果矩阵是一个2行3列的矩阵。
分析:
矩阵A包含2个三维向量,矩阵B包含3个三维向量,矩阵B可以代表三维空间中的一个三维立体子空间,所以A中的所有向量投影到B,最终的结果变成了2个三维向量,符合我们对向量点乘及矩阵的理解。
3.2.7 和书本理论进行比较
书本上的矩阵规则和我们理解的矩阵只有一点不同。还是以
A ∗ B = C A * B = C A∗B=C
为例。
书本上将矩阵B,进行了转置。也就是说,B矩阵中的向量,按照我们的理解,应该一行一行依次摆放,但是书本上规定应该竖着依次摆放。为什么?因为书本规定,矩阵A乘矩阵B,矩阵A的每一个行向量要和矩阵B的每一个列向量进行点乘,而我们的运算规则是矩阵A的每一个行向量要和矩阵B的每一个行向量进行点乘,所以在书本上规定的运算规则下,必须将向量B进行转置。其实运算结果和原理是完全一样的。
3.2.8 特别的变换
如果矩阵B为三行三列的单位矩阵(单位矩阵用E表示),即
B = E = ( 1 0 0 0 1 0 0 0 1 ) B = E = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} B=E= 100010001
任意一个m行3列的矩阵A,乘以矩阵B,都等于矩阵A本身,即
A ∗ B = A ∗ E = A A * B = A * E = A A∗B=A∗E=A
这个大家可以自己尝试演算一下。我们这里不做演算,我们这里做一个理论分析:
B矩阵为单位矩阵时,B矩阵所代表的空间,和当前的整个三维空间完全重合。矩阵A乘矩阵B,就是将矩阵A变换到原空间,而且不改变向量的长度,那么变换结果必然也和A重合,也就是说结果等于A。通过分析,我们可以很容易地理解,为什么一个矩阵乘以单位矩阵,结果是它本身。
下一篇:《矩阵乘法进阶》
相关文章:
线性运算的推广与矩阵基础)
【理解线性代数】(四)线性运算的推广与矩阵基础
1. 数值加法和乘法 数值加法与乘法,是小学数学课程中的基本数学运算。例如: 加法:112 乘法:2*24 在这个知识层次下,运算的基本单位是数字。 2. 从数值到向量 数值加法,可以看作一维空间中的向量加法&…...

C# 什么是继承和派生
C# 什么是继承和派生 在 C# 中,继承(Inheritance)是一种机制,它允许一个类(子类)从另一个类(父类)中继承属性和方法。这种关系使得子类可以重用父类的代码,同时可以在子…...

无涯教程-JavaScript - HEX2BIN函数
描述 HEX2BIN函数将十六进制数转换为二进制数。 语法 HEX2BIN (number, [places])争论 Argument描述Required/Optionalnumber 您要转换的十六进制数。 数字不能超过10个字符(40位)。数字的最高有效位是符号位(从右数第40位)。其余的39位是幅度位。 负数使用二进制补码表示。…...
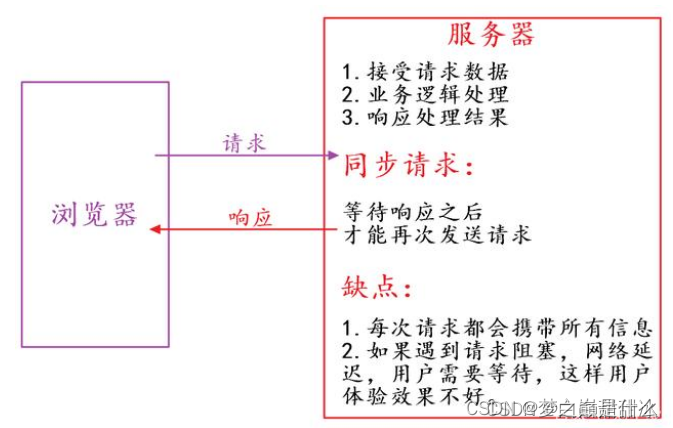
前端面试0906
// 请给出输出结果 function foo(){ console.log(a); } function bar(){ var a 3; console.log(this.a); foo(); } var a 2; bar(); 2 2 // 请从下面的问题中挑选3道进行回答 1. 防抖和节流分别是什么,一般用在什么场景? 防抖(Debounc…...

OceanBase社区版4.x核心技术解密
数字化时代,各行各业的数据量呈现爆发式增长,对于海量数据价值的挖掘和应用,正成为推动创新的主要力量,与此同时,数据计算复杂度正在提升。在此背景下,对于数据处理的基石数据库而言,正面临市场…...

快速安装k8s
RKE安装方式 官方文章资源地址 https://rke.docs.rancher.com/installation rke工具下载地址(arm,amd,windows都有) https://github.com/rancher/rke/releases x86的用amd64下载rke工具 https://github.com/rancher/rke/releases/download/v1.4.8/rke_li…...

[FFmpeg] 常用ffmpeg命令
去水印 ffmpeg -i water.jpeg -strict -2 -vf delogox300:y250:w56:h18:show0 no_water.jpeg 打时间戳 ffmpeg -i perf_60Hz_Raw.mp4 -vf "drawtextfontsize160:fontcolorred:text%{pts\:hms}" -c:v libx264 -an -f mp4 perf_output.mp4 -y ffmpeg -i perf_8k.mp4 -v…...

代码随想录训练营第五十七天|647. 回文子串、516.最长回文子序列
647. 回文子串 题目链接/文章讲解/视频讲解:代码随想录 1.代码展示 //647.回文子串 int countSubstrings(string s) {//step1 构建dp数组,明确dp数组的含义,dp[i][j]的含义是在下标为i和j区间内的字串是否为回文串vector<vector<bool&…...
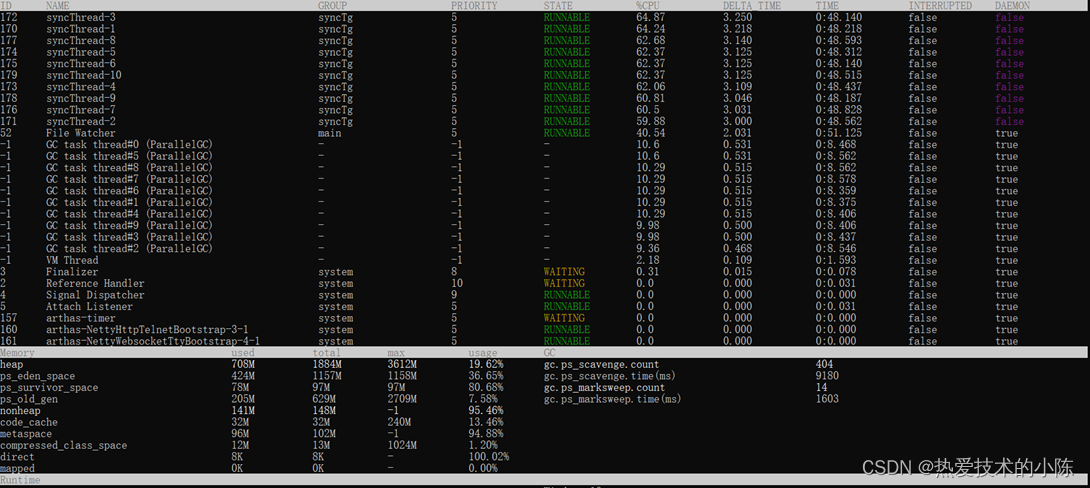
对线程池设置做压测
线程池代码 Configuration public class ThreadPoolConfig {// 核心线程池大小private int corePoolSize 24;// 最大可创建的线程数private int maxPoolSize 25;// 队列最大长度private int queueCapacity 100;// 线程池维护线程所允许的空闲时间private int keepAliveSeco…...

【网络通信 -- WebRTC】项目实战记录 -- mediasoup android 适配 webrtc m94
【网络通信 -- WebRTC】项目实战记录 -- mediasoup android 适配 webrtc m94 【1】下载并配置 depot_tools 下载 depot_tools git clone https://chromium.googlesource.com/chromium/tools/depot_tools.git编辑 ~/.bashrc 将 depot_tools 添加到路径中 vim ~/.bashrc export…...
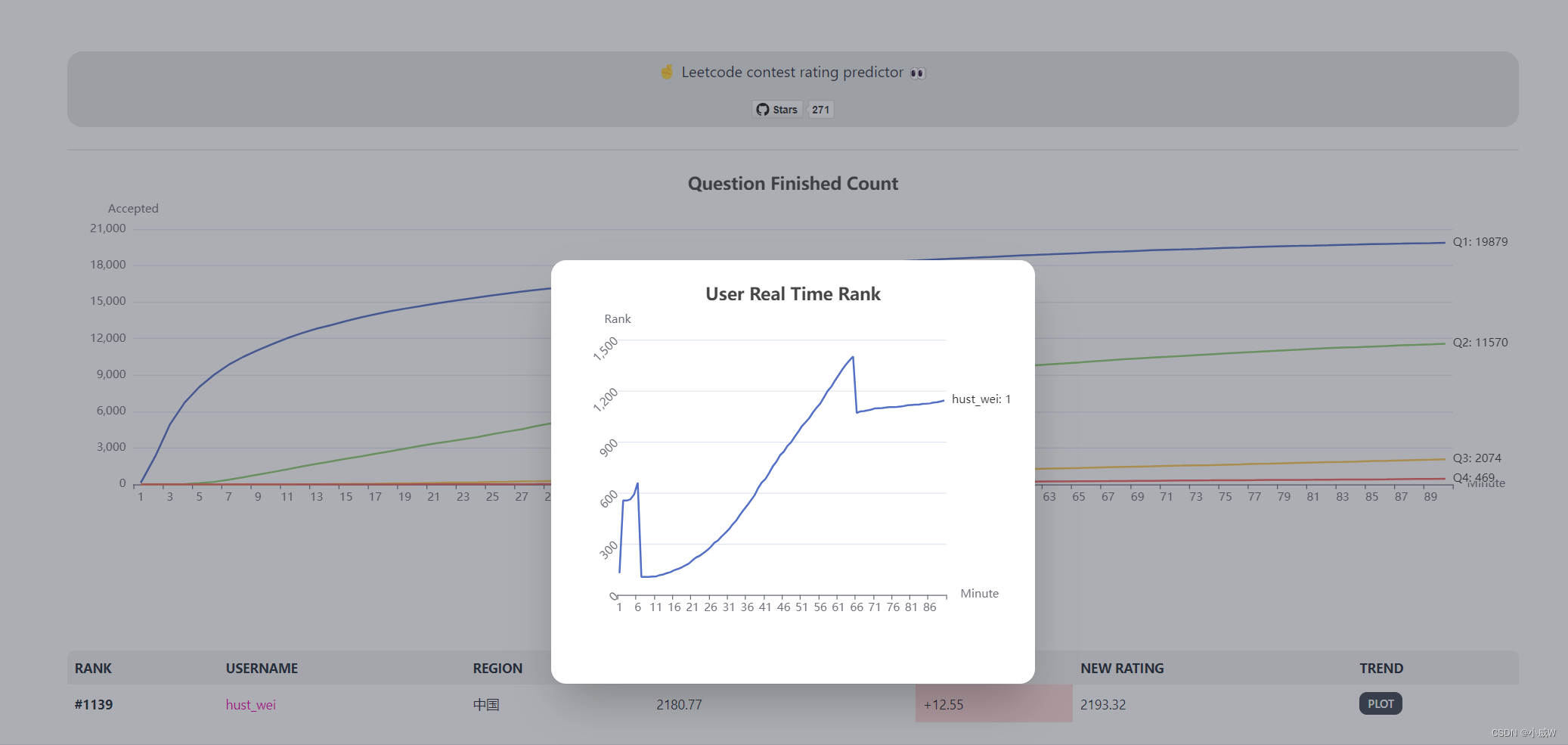
【力扣周赛】第 357 场周赛(⭐反悔贪心)
文章目录 竞赛链接Q1:6925. 故障键盘解法1——直接模拟解法2——双端队列 Q2:6953. 判断是否能拆分数组(贪心)Q3:2812. 找出最安全路径⭐解法1——多源BFS瓶颈路模型?解法2——多源BFS 倒序枚举答案 并查…...

css重置
css 重置 CSS 重置的主要目标是确保浏览器之间的一致性,并撤消所有默认样式,创建一个空白板。 如今,主流浏览器都实现了css规范,在布局或间距方面没有太大差异。但是通过自定义 CSS 重置,也可以改善用户体验和提高开…...

tcpdump相关
Linux内核角度分析tcpdump原理(一)Linux内核角度分析tcpdump原理(二)...

MFC新建内部消息
提示:记录一下MFC新建内部消息的成功过程 文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 先说一下基本情况,因为要在mapview上增加一个显示加载时间的功能。然后发现是要等加载完再显示时间,显示在主…...

linux查找目录
要在Linux中查找目录,可以使用find命令。下面是查询目录的几个示例: 1,查找当前目录下所有子目录: find . -type d 2,在指定路径下查找目录: find /path/to/directory -type d 3,查找以特定名称开头的目录: find . -t…...
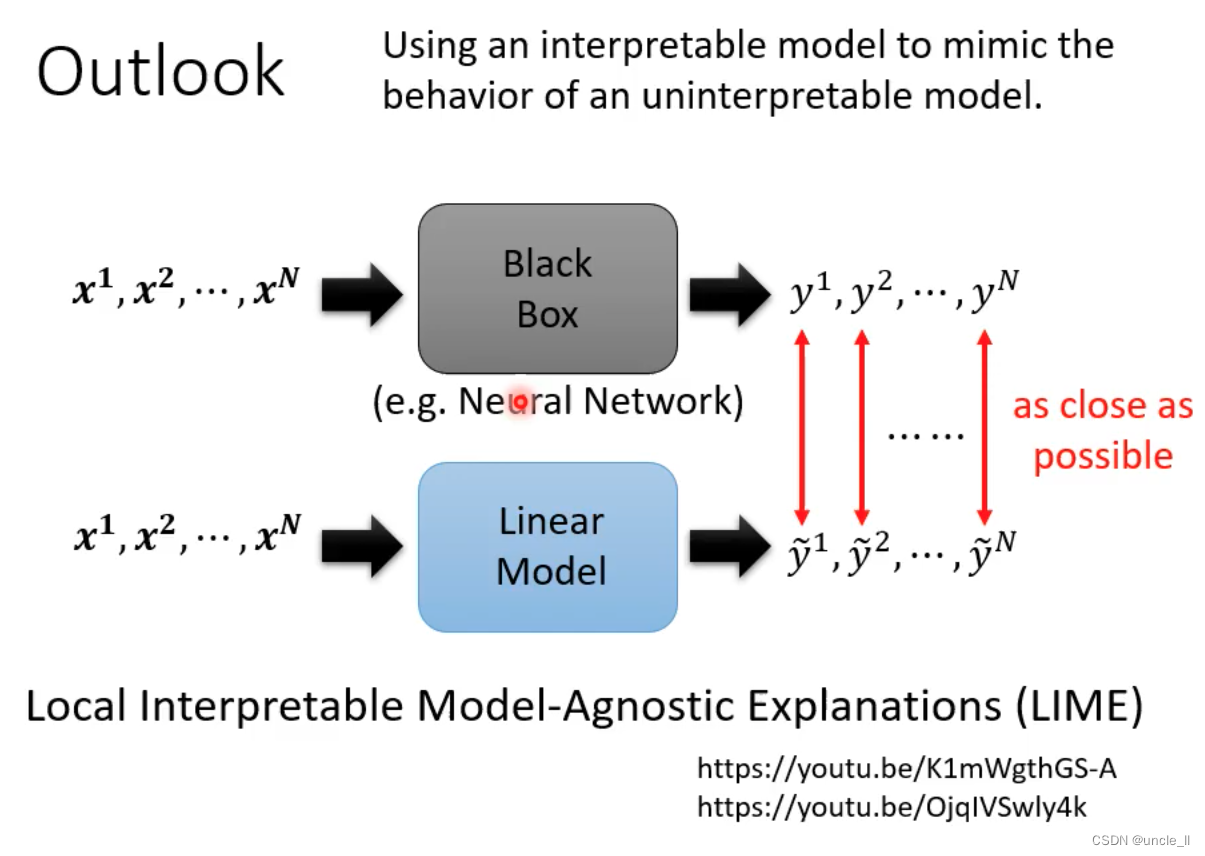
机器学习:可解释学习
文章目录 可解释学习为什么需要可解释机器学习可解释还是强模型可解释学习的目标可解释机器学习Local ExplanationGlobal Explanation 可解释学习 神马汉斯,只有在有人看的时候能够答对。 为什么需要可解释机器学习 贷款,医疗需要给出理由,让…...

UE5- c++ websocket里实现调用player里的方法
# UGameInstance里直接调用 获取到引用了,就可以自然的调用。忽略 # UGameInstance里间接调用,通过代理调用 前置已经添加了websocket,具体步骤参考,链接在UWebSocketGameInstance.h里新增代理,并在链接成功后进行绑定。 #pragma…...
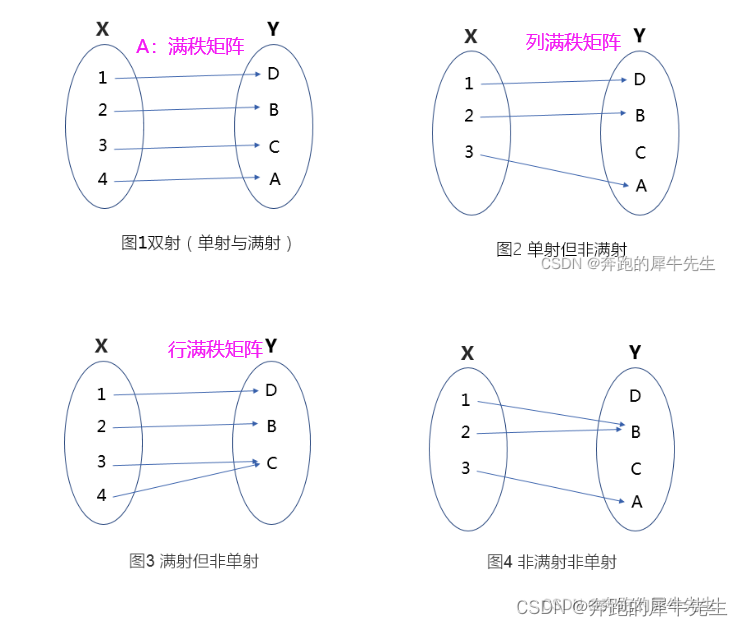
线性代数的学习和整理18:什么是维度,什么是秩?秩的各种定理秩的计算 (计算部分未完成)
目录 0 问题引出:什么是秩? 概念备注: 1 先厘清:什么是维数? 1.1 真实世界的维度数 1.2 向量空间的维数 1.2.1 向量空间,就是一组最大线性无关的向量组/基张成的空间 1.3 向量α的维数 1.3.1 向量的…...
Centos 6.5 升级到Centos7指导手册
一、背景 某业务系统因建设较早,使用的OS比较过时,还是centos6.5的系统,因国产化需要,需将该系统升级到BClinux 8.6,但官方显示不支持centos 6.x升级到8,需先将centos6.5升级到centos7的最新版,…...

详解python中的映射类型---字典
概述 映射类型是“键-值”数据项的组合,每个元素是一个键值对,即元素是(key,value),元素之间是无序的。键值对(key,value)是一种二元关系,源于属性和值的映射…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
