【LeetCode75】第四十九题 数组中的第K个最大元素
目录
题目:
示例:
分析:
代码:
题目:

示例:
分析:
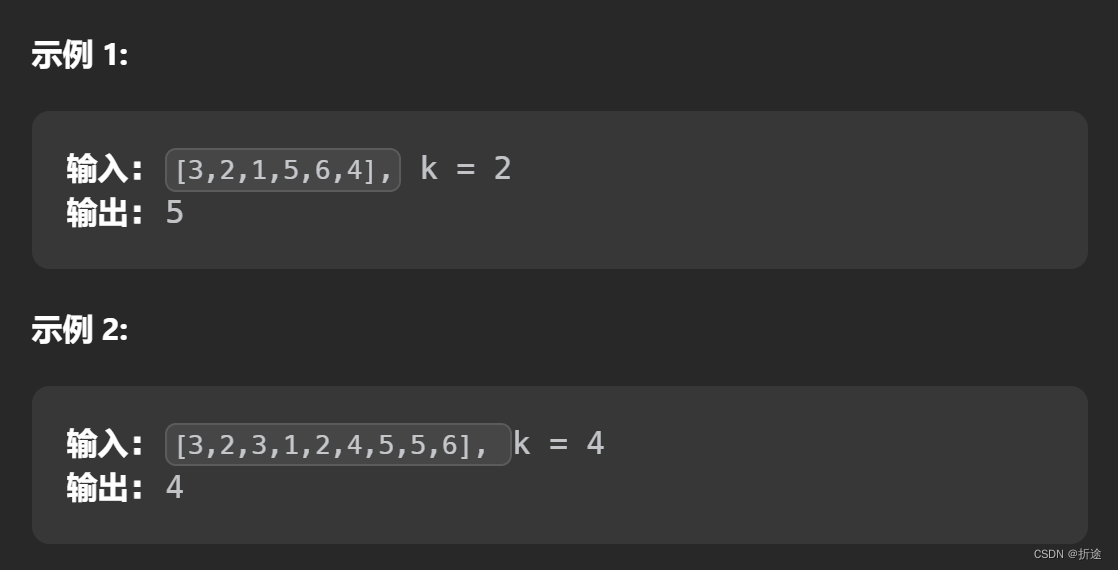
题目很简单,就是给我们一个数组,让我们返回第K大的元素。
那么很直观的一个做法就是我们直接对数组进行降序排序,索引为k-1的元素就是整个数组里第k大的元素了。
另外一个就是使用大顶堆,C++里有内置,是叫priority_queue优先队列,我们只需要往优先队列里塞进元素,那么这个容器底层会自动对元素进行排序,我们从大顶堆里取的数永远是队列里最大的数,那么我们只需要取数,再将大顶堆的堆顶元素移出,如此反复k-1次,那么最后取出的数就是数组里第K大的元素了。
至于大顶堆该怎么实现,我的看法是我们普通人只需要会使用内置的容器就可以了,真的要自己手写一个大顶堆的话还是挺麻烦的。
代码:
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {//使用C++内置优先队列 大顶堆priority_queue<int>pq(nums.begin(),nums.end());for(int i=0;i<k-1;i++){pq.pop();}return pq.top();//从大到小排序后返回第K大的元素sort(nums.begin(),nums.end(),[](int a,int b){return a>b;});return nums[k-1];}
};相关文章:

【LeetCode75】第四十九题 数组中的第K个最大元素
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目很简单,就是给我们一个数组,让我们返回第K大的元素。 那么很直观的一个做法就是我们直接对数组进行降序排序…...
嵌入式面试笔试刷题(day14)
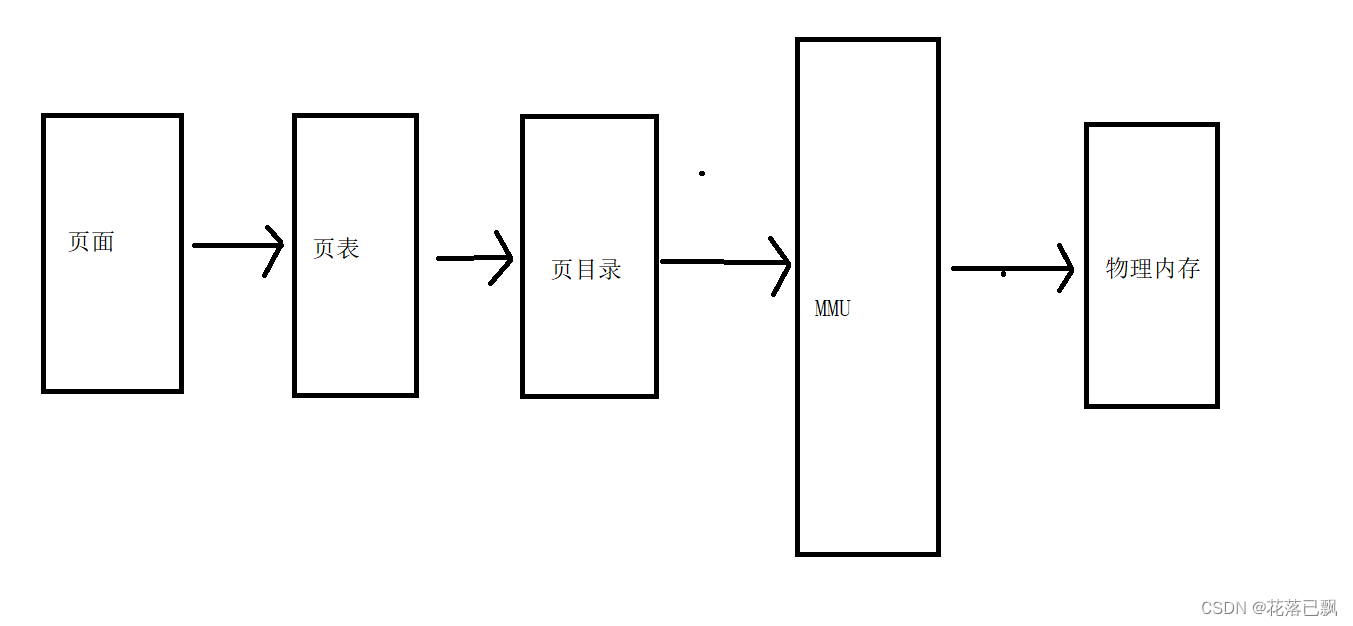
文章目录 前言一、进程控制块1.PCB控制块的作用2.PCB的存储位置 二、进程的三级映射三、return , exit, pthread_exit四、pthread_join作用五、互斥锁和信号量的区别六、怎么判断链表是否有环总结 前言 本篇文章继续我们的刷题之路。 一、进程控制块 这里只讲解进程的PCB控制…...
好用免费的Chat GPT(亲测有用)
1、MindLink麦灵 MindLink麦灵 点进登录后 普通用户可以提问100次 2、你问我答 你问我答 无限次数的。 3、灵感 灵感 点击链接后会提示你如何下载使用。 这个有win版和mac版,点击登陆后,每日都会有30次GPT3/3.5的提问。 4、WebTab 在浏览器插件中…...
SpringBoot项目--电脑商城【上传头像】
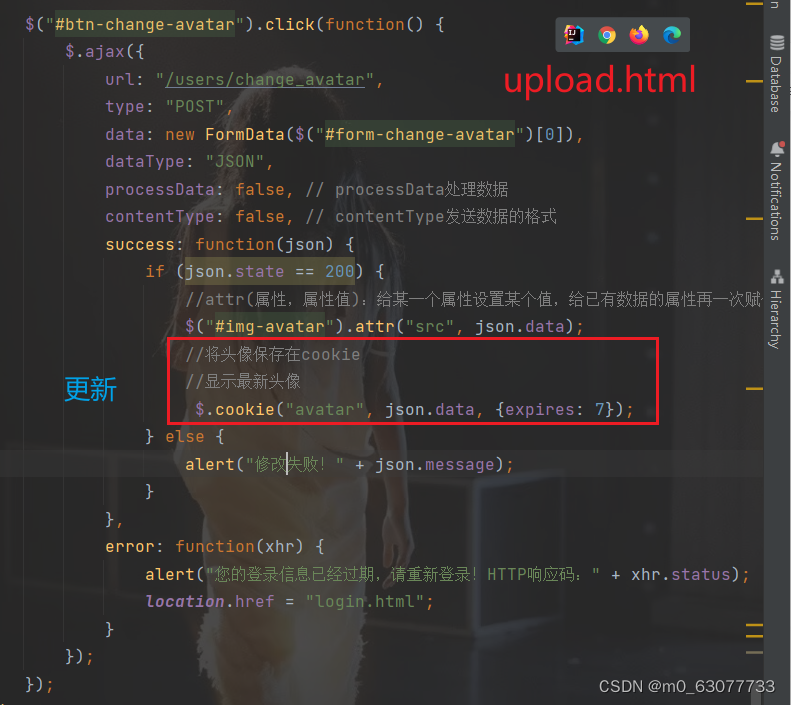
一、易错点 1.错误写法: 把文件存到数据库中,需要图片时访问数据库,数据库将文件解析为字节流返回,最后写到本地的某一个文件.这种方法太耗费资源和时间了 2.正确写法: 将对应的文件保存在操作系统上,然后再把这个文件路径记录下来,因为在记录路径的…...

优化SOCKS5的方法
在今天的互联网世界中,保护个人隐私和提升网络速度至关重要。作为一种常用的代理协议,SOCKS5代理服务器不仅可以保护您的隐私,还可以实现更快速的网络访问。本文将为您介绍一些优化SOCKS5代理服务器的方法,以提高网络速度和安全性…...

使用 HelpLook Chatbot,让AI聊天机器人变成销售经理
想要增强AI聊天机器人销售技巧的话,我们需要一个强大的搭建工具来帮助我们增加客户互动,通过很多的客户互动数据来支撑和锻炼我们的AI聊天机器人。在本篇文章中,looklook将会系统地来说说该如何定制聊天机器人的行为。 使用AI聊天机器人的好处…...
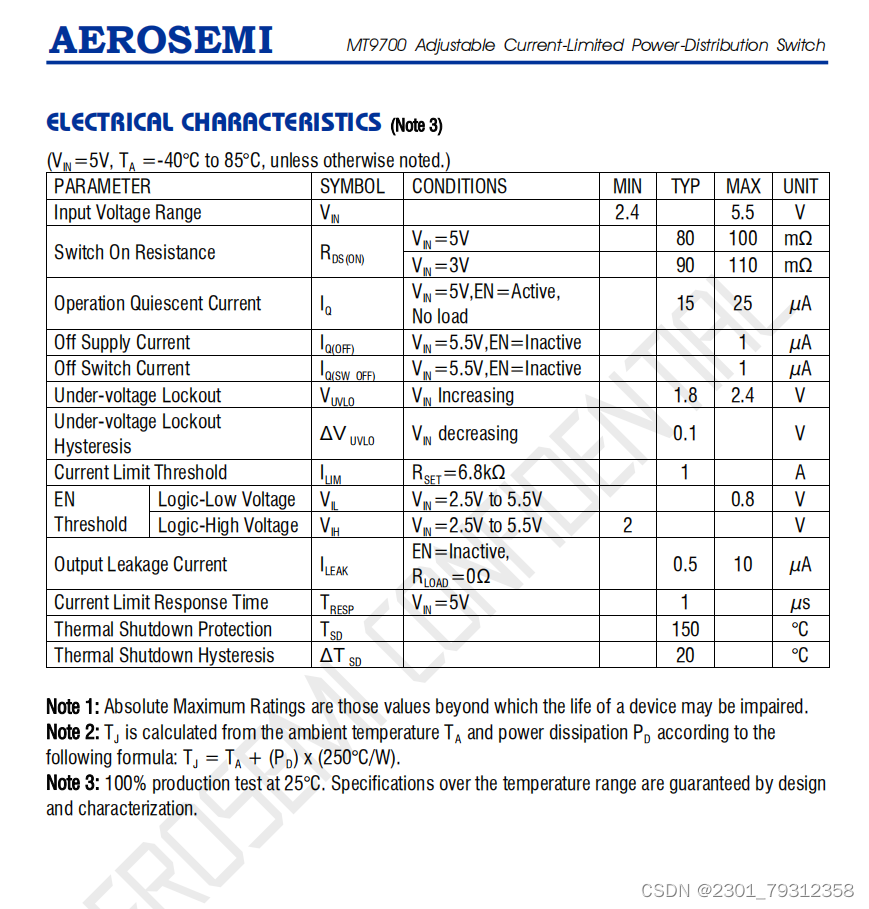
MT9700 80mΩ,可调快速响应限流配电开关芯片
MT9700 80mΩ,可调快速响应限流配电开关芯片 特征 符合USB规范 集成80mΩ电源MOSFET 低电源电流 15μA典型开启状态 1μA典型关闭状态 宽输入电压Range:2.4V到5.5V 快速瞬态响应:<2μs 反向电流流阻塞 热关机保护 热插件应…...

RabbitMQ之延迟队列
RabbitMQ之延迟队列 1. 延迟队列概念2. 延迟队列使用场景3. RabbitMQ 中的 TTL3.1 消息设置 TTL3.2 队列设置 TTL3.3 两者的区别 4. 整合 SpringBoot4.1 创建项目4.2 添加依赖4.3 修改配置文件4.4 添加 Swagger 配置类 5. 队列 TTL5.1 代码架构图5.2 配置文件类代码5.3 消息生产…...

k8s部署手册-v06
一、基础配置 1.修改主机名 hostnamectl set-hostname k8s-master01 hostnamectl set-hostname k8s-master02 hostnamectl set-hostname k8s-master03 hostnamectl set-hostname k8s-node01 hostnamectl set-hostname k8s-node022.添加 主机名与IP地址解析 cat > /etc/ho…...

Qt 5.15集成Crypto++ 8.7.0(MSVC 2019)笔记
一、背景 笔者已介绍过在Qt 5.15.x中使用MinGW(8.10版本)编译并集成Crypto 8.7.0。 但是该编译出来的库(.a和.dll)不适用MSVC(2019版本)构建环境,需要重新编译(.lib或和.dll…...
)
LeetCode——贪心篇(一)
刷题顺序及思路来源于代码随想录,网站地址:https://programmercarl.com 目录 455. 分发饼干 376. 摆动序列 53. 最大子数组和 122. 买卖股票的最佳时机 II 55. 跳跃游戏 45. 跳跃游戏 II 1005. K 次取反后最大化的数组和 455. 分发饼干 假设你是…...

2023高教社杯 国赛数学建模C题思路 - 蔬菜类商品的自动定价与补货决策
1 赛题 在生鲜商超中,一般蔬菜类商品的保鲜期都比较短,且品相随销售时间的增加而变差, 大部分品种如当日未售出,隔日就无法再售。因此, 商超通常会根据各商品的历史销售和需 求情况每天进行补货。 由于商超销售的蔬菜…...
线性运算的推广与矩阵基础)
【理解线性代数】(四)线性运算的推广与矩阵基础
1. 数值加法和乘法 数值加法与乘法,是小学数学课程中的基本数学运算。例如: 加法:112 乘法:2*24 在这个知识层次下,运算的基本单位是数字。 2. 从数值到向量 数值加法,可以看作一维空间中的向量加法&…...

C# 什么是继承和派生
C# 什么是继承和派生 在 C# 中,继承(Inheritance)是一种机制,它允许一个类(子类)从另一个类(父类)中继承属性和方法。这种关系使得子类可以重用父类的代码,同时可以在子…...

无涯教程-JavaScript - HEX2BIN函数
描述 HEX2BIN函数将十六进制数转换为二进制数。 语法 HEX2BIN (number, [places])争论 Argument描述Required/Optionalnumber 您要转换的十六进制数。 数字不能超过10个字符(40位)。数字的最高有效位是符号位(从右数第40位)。其余的39位是幅度位。 负数使用二进制补码表示。…...
前端面试0906
// 请给出输出结果 function foo(){ console.log(a); } function bar(){ var a 3; console.log(this.a); foo(); } var a 2; bar(); 2 2 // 请从下面的问题中挑选3道进行回答 1. 防抖和节流分别是什么,一般用在什么场景? 防抖(Debounc…...

OceanBase社区版4.x核心技术解密
数字化时代,各行各业的数据量呈现爆发式增长,对于海量数据价值的挖掘和应用,正成为推动创新的主要力量,与此同时,数据计算复杂度正在提升。在此背景下,对于数据处理的基石数据库而言,正面临市场…...

快速安装k8s
RKE安装方式 官方文章资源地址 https://rke.docs.rancher.com/installation rke工具下载地址(arm,amd,windows都有) https://github.com/rancher/rke/releases x86的用amd64下载rke工具 https://github.com/rancher/rke/releases/download/v1.4.8/rke_li…...

[FFmpeg] 常用ffmpeg命令
去水印 ffmpeg -i water.jpeg -strict -2 -vf delogox300:y250:w56:h18:show0 no_water.jpeg 打时间戳 ffmpeg -i perf_60Hz_Raw.mp4 -vf "drawtextfontsize160:fontcolorred:text%{pts\:hms}" -c:v libx264 -an -f mp4 perf_output.mp4 -y ffmpeg -i perf_8k.mp4 -v…...

代码随想录训练营第五十七天|647. 回文子串、516.最长回文子序列
647. 回文子串 题目链接/文章讲解/视频讲解:代码随想录 1.代码展示 //647.回文子串 int countSubstrings(string s) {//step1 构建dp数组,明确dp数组的含义,dp[i][j]的含义是在下标为i和j区间内的字串是否为回文串vector<vector<bool&…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
