【数据结构】 七大排序详解(壹)——直接插入排序、希尔排序、选择排序、堆排序
文章目录
- 🍀排序的概念及引用
- 🐱👤排序的概念
- 🐱👓排序运用
- 🐱🐉常见的排序算法
- 🌴插入排序
- 🎋基本思想:
- 🛫直接插入排序
- 📌算法步骤:
- 📌代码实现:
- 📌直接插入排序特性:
- 🛬希尔排序( 缩小增量排序 )
- 📌算法步骤:
- 📌代码实现:
- 📌希尔排序的特性总结
- 🌳选择排序
- 🎋基本思想
- 🛫直接选择排序
- 🚩 算法步骤:
- 🚩代码实现:
- 🚩直接选择排序的特性总结
- 🎄堆排序
- 🚩算法步骤
- 🚩代码实现:
- 🚩堆排序的特性总结
- ⭕总结
🍀排序的概念及引用
🐱👤排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。

内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序
🐱👓排序运用
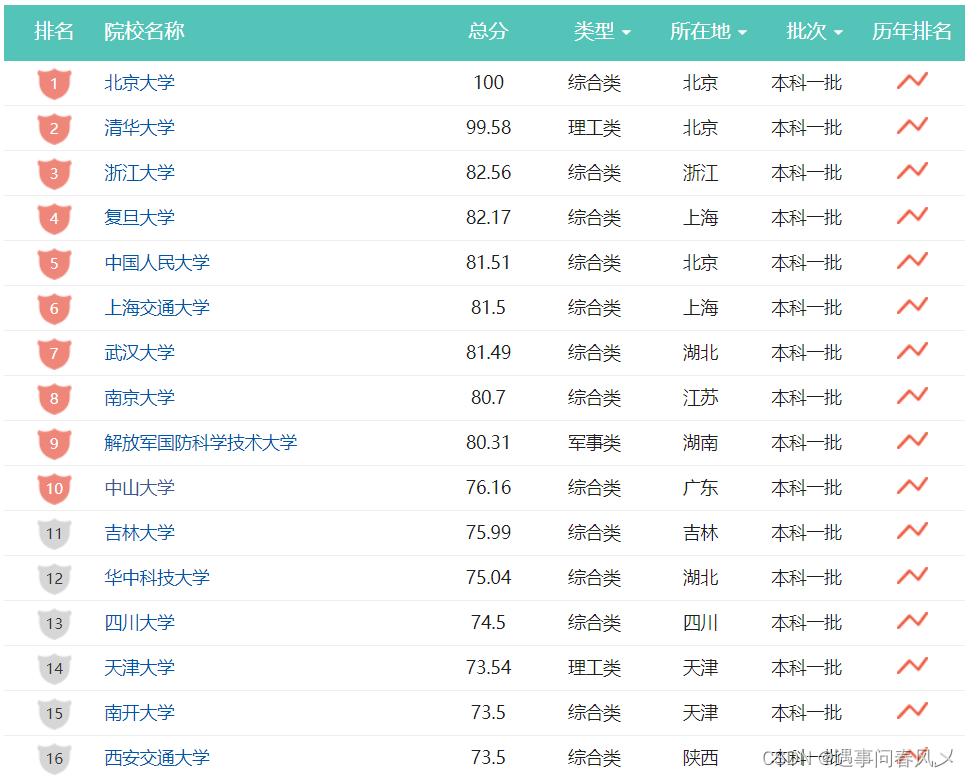
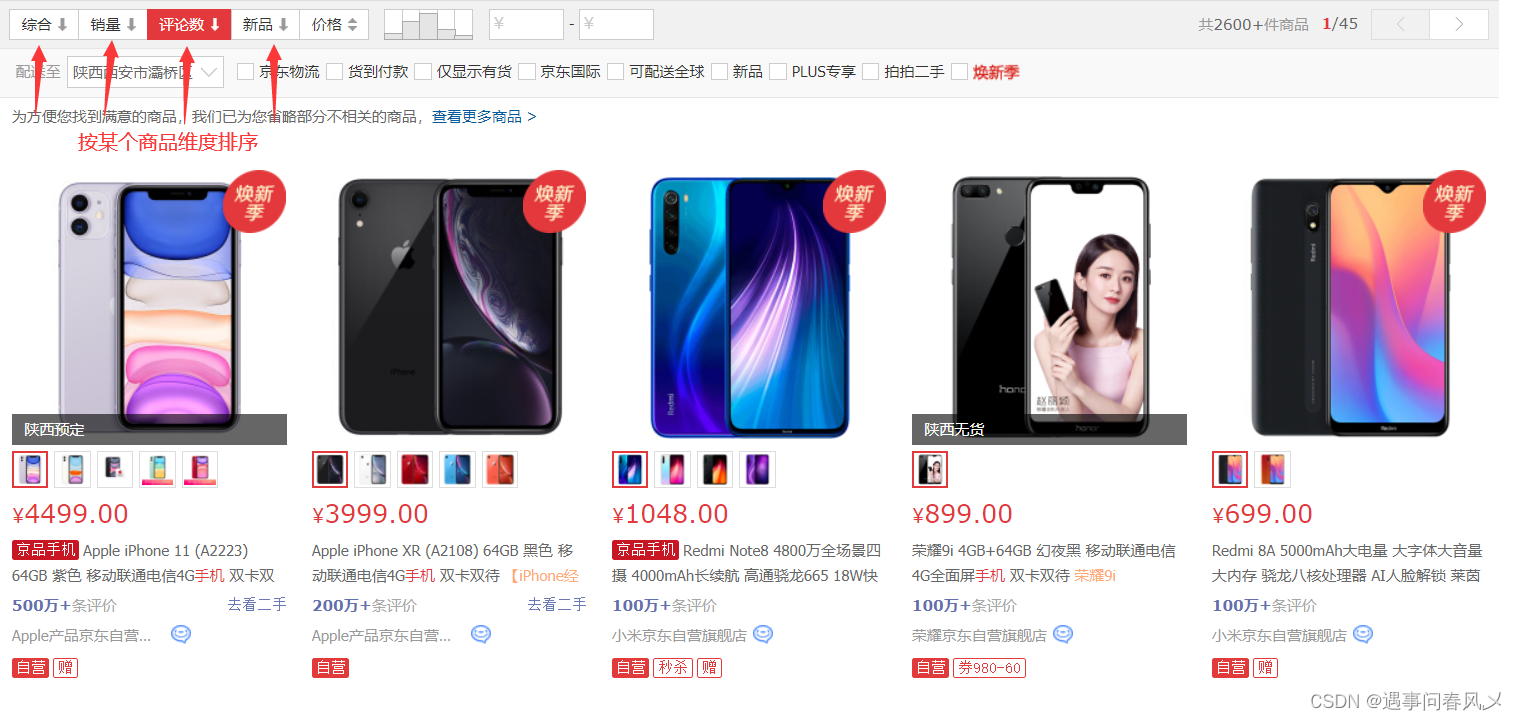
比如我们在逛淘宝时
🐱🐉常见的排序算法
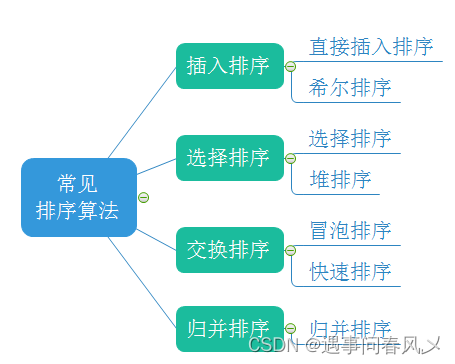
本篇博客将着重讲解前四种算法
🌴插入排序
🎋基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想。

🛫直接插入排序
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。
📌算法步骤:
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)

即当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
📌代码实现:
public void straightInsertion(int[] array) {int len = array.length;for(int i = 1; i < len ; i++) {int count = array[i];int j = i - 1;for( ; j >= 0; j --) {if(count < array[j]) {array[j + 1] = array[j];} else {break;}}array[j + 1] = count;}}
📌直接插入排序特性:
-
元素集合越接近有序,直接插入排序算法的时间效率越高
-
时间复杂度:O(N^2)
-
空间复杂度:O(1),它是一种稳定的排序算法
-
稳定性:稳定
🛬希尔排序( 缩小增量排序 )
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位;
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序
📌算法步骤:
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 gap,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。

动图演示如下:

📌代码实现:
public void straightInsertion(int[] array,int gap) {int len = array.length;for(int i = gap; i < len ; i++) {int count = array[i];int j = i - gap;for( ; j >= 0; j-=gap) {if(count < array[j]) {array[j + gap] = array[j];} else {break;}}array[j + gap] = count;}}public void shellSort(int[] arrary) {int gap = arrary.length;while(gap > 0) {gap = gap /2;straightInsertion(arrary,gap);}}📌希尔排序的特性总结
-
希尔排序是对直接插入排序的优化。
-
当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
-
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定,以下来自大佬的给出的解释
《数据结构(C语言版)》— 严蔚敏

《数据结构-用面向对象方法与C++描述》— 殷人昆

- 稳定性:不稳定
🌳选择排序
🎋基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
🛫直接选择排序
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
🚩 算法步骤:
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
即:
-
在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
-
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
-
在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素

🚩代码实现:
public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;int j = i+1;for (; j < array.length; j++) {if(array[j] < array[minIndex]) {minIndex = j;}}swap(array,i,minIndex);}}private static void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
🚩直接选择排序的特性总结
-
直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
-
时间复杂度:O(N^2)
-
空间复杂度:O(1)
-
稳定性:不稳定
🎄堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
-
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
-
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;
🚩算法步骤
-
创建一个堆 H[0……n-1];
-
把堆首(最大值)和堆尾互换;
-
把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
-
重复步骤 2,直到堆的尺寸为 1。
如下图所示:

🚩代码实现:
private void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public void heapSort(int[] array) {createBigHeap(array);int end = array.length-1;while (end > 0) {swap(array,0,end);shiftDown(array,0,end);end--;}}private void createBigHeap(int[] array) {for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {shiftDown(array,parent,array.length);}}private void shiftDown(int[] array,int parent,int len) {int child = 2*parent+1;while (child < len) {if(child+1 < len && array[child] < array[child+1]) {child++;}if(array[child] > array[parent]) {swap(array,child,parent);parent = child;child = 2*parent+1;}else {break;}}}
🚩堆排序的特性总结
-
堆排序使用堆来选数,效率就高了很多。
-
时间复杂度:O(N*logN)
-
空间复杂度:O(1)
-
稳定性:不稳定
⭕总结
关于《【数据结构】 七大排序详解(壹)——直接插入排序、希尔排序、选择排序、堆排序》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!
相关文章:

【数据结构】 七大排序详解(壹)——直接插入排序、希尔排序、选择排序、堆排序
文章目录 🍀排序的概念及引用🐱👤排序的概念🐱👓排序运用🐱🐉常见的排序算法 🌴插入排序🎋基本思想:🛫直接插入排序📌算法步骤&…...
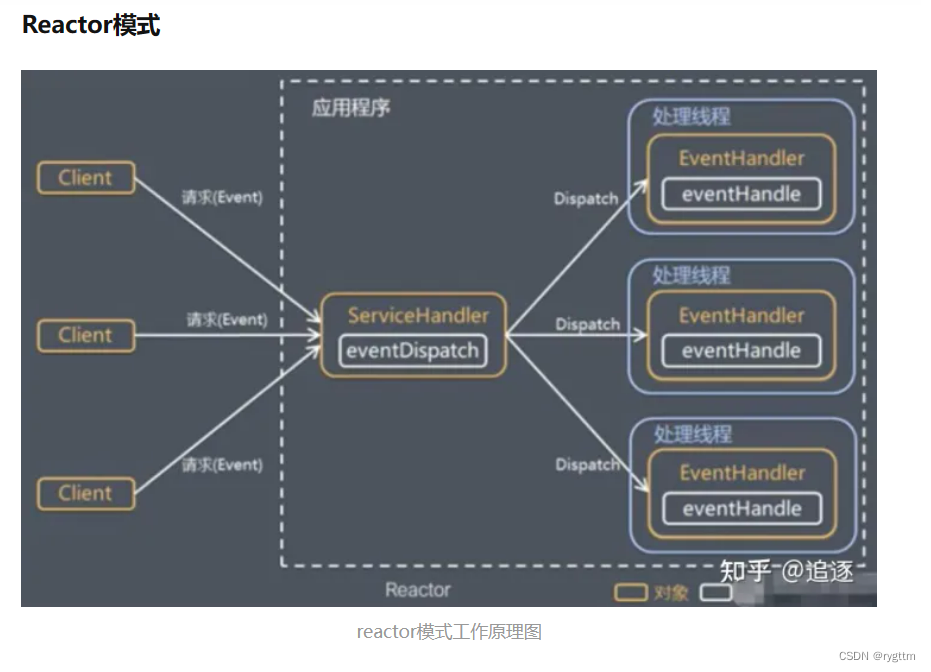
【Linux】高级IO --- Reactor网络IO设计模式
人其实很难抵制诱惑,人只能远离诱惑,所以千万不要高看自己的定力。 文章目录 一、LT和ET模式1.理解LT和ET的工作原理2.通过代码来观察LT和ET工作模式的不同3.ET模式高效的原因(fd必须是非阻塞的)4.LT和ET模式使用时的读取方式 二…...
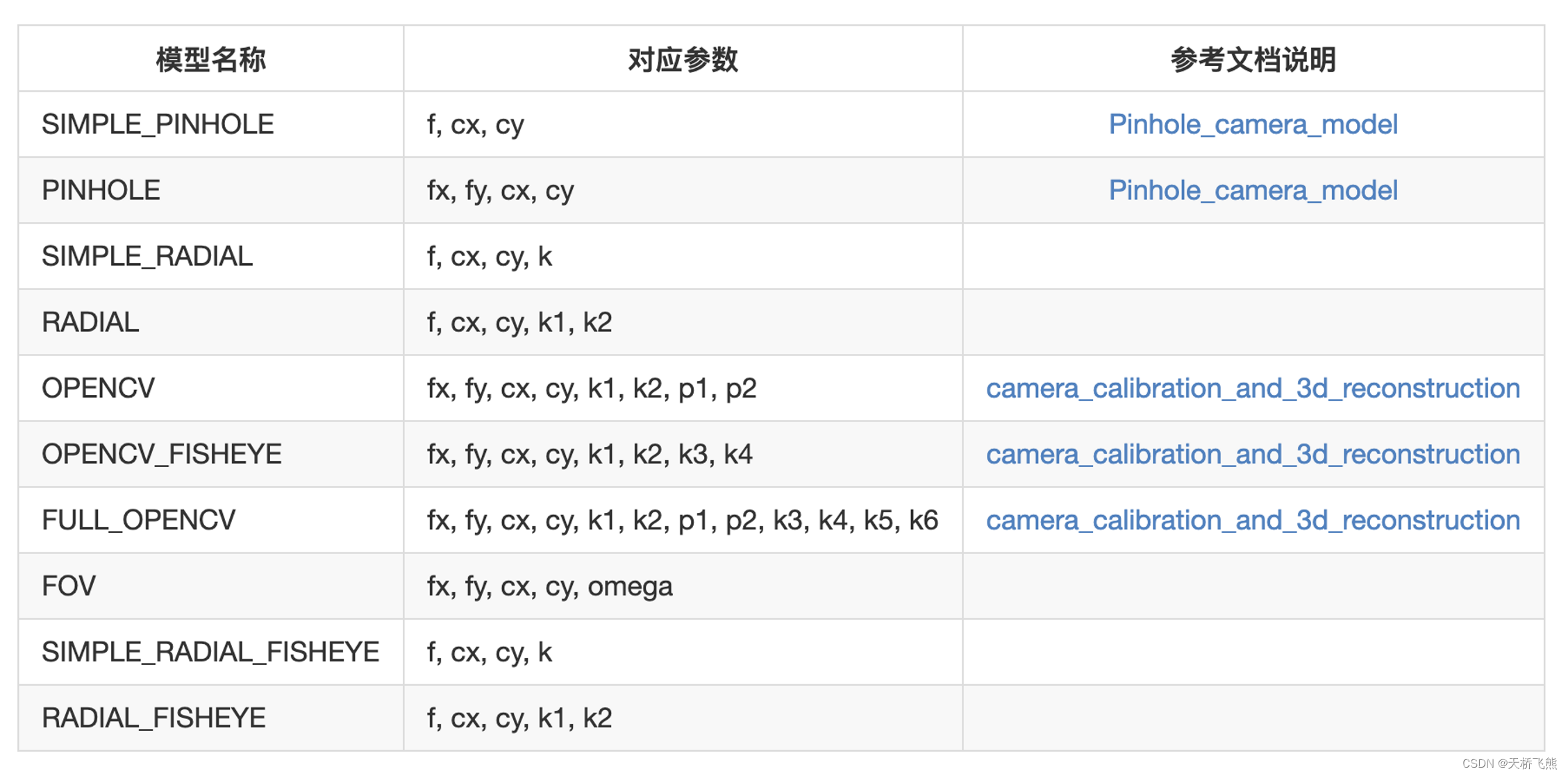
Agisoft Metashape相机标定笔记
Lens Calibration(镜头标定) 使用Metashape进行自动相机标定是可能的。Metashape使用LCD显示屏作为标定目标(可选:使用打印的棋盘格图案,但需保证它是平坦的且单元格是正方形)。 相机标定步骤支持全相机标定矩阵的估计ÿ…...

vue-cropper在ie11下选择本地图片后,无显示、拒绝访问的问题
问题:vue-cropper在ie11下选择本地图片后,网页上并未显示出图片,打开F12有报错:拒绝访问blabla的。但是在chrome下一切正常。 开发环境:node14.17.5 , vue2 , vue-cropper0.6.2 , macOS big sur 11.4(M1). 解决办法&…...
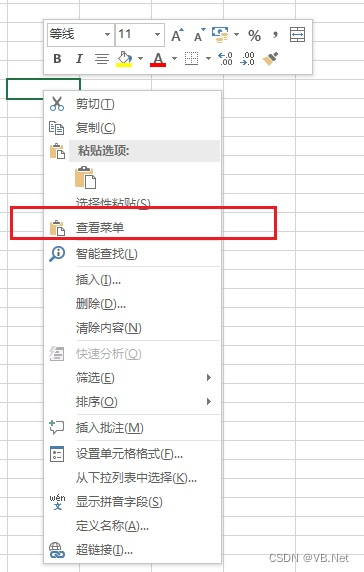
Excel VSTO开发11-自定义菜单项
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 11 自定义菜单项 自定义菜单项可以在插件启动时候添加,即增加到ThisAddIn_Startup() 内。 下面以具体代码说明&#x…...
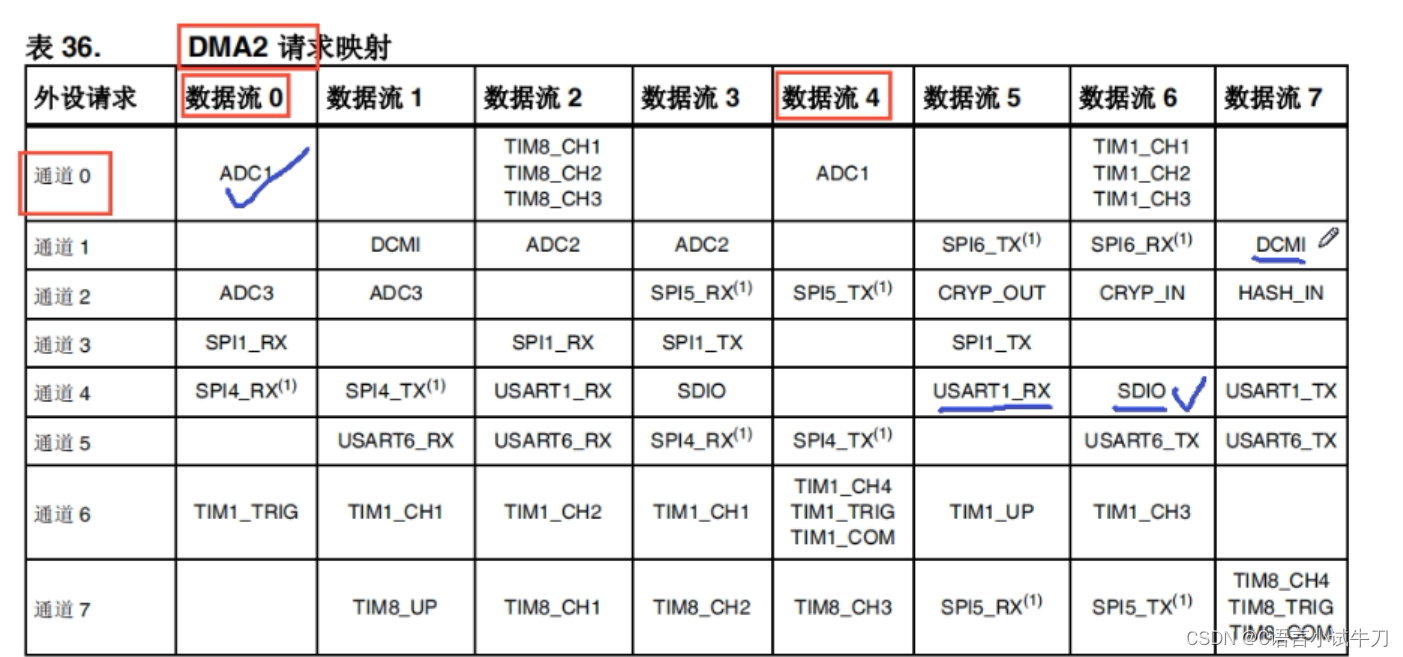
stm32之30.DMA
DMA(硬件加速方法)一般用于帮运比较大的数据(如:摄像头数据图像传输),寄存器-》DMA-》RAM 或者 RAM-》DMA-》寄存器提高CPU的工作效率 源码-- #include "myhead.h" #include "adc.h"#…...
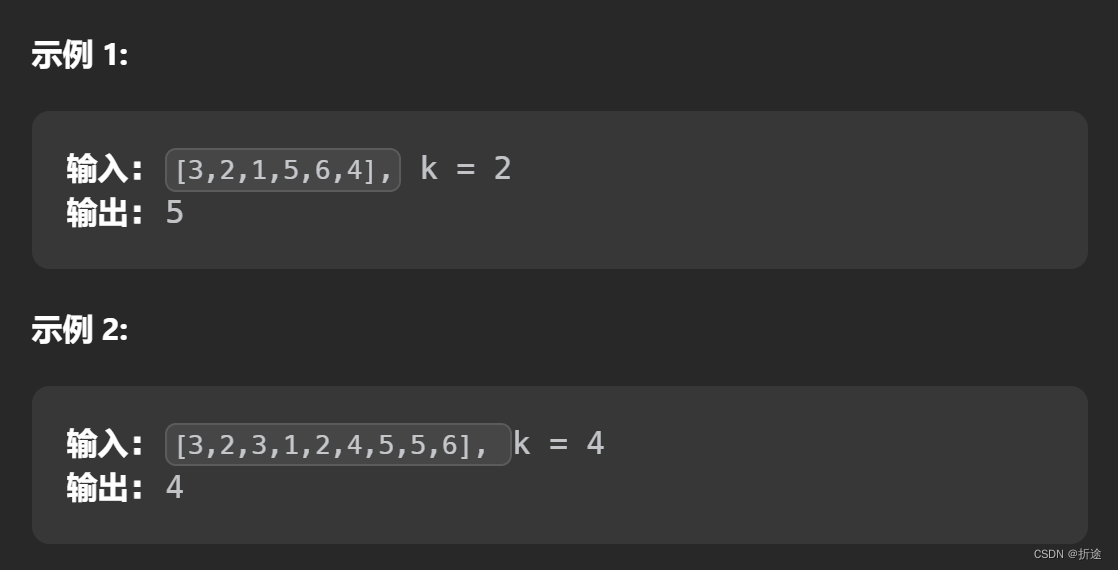
【LeetCode75】第四十九题 数组中的第K个最大元素
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目很简单,就是给我们一个数组,让我们返回第K大的元素。 那么很直观的一个做法就是我们直接对数组进行降序排序…...
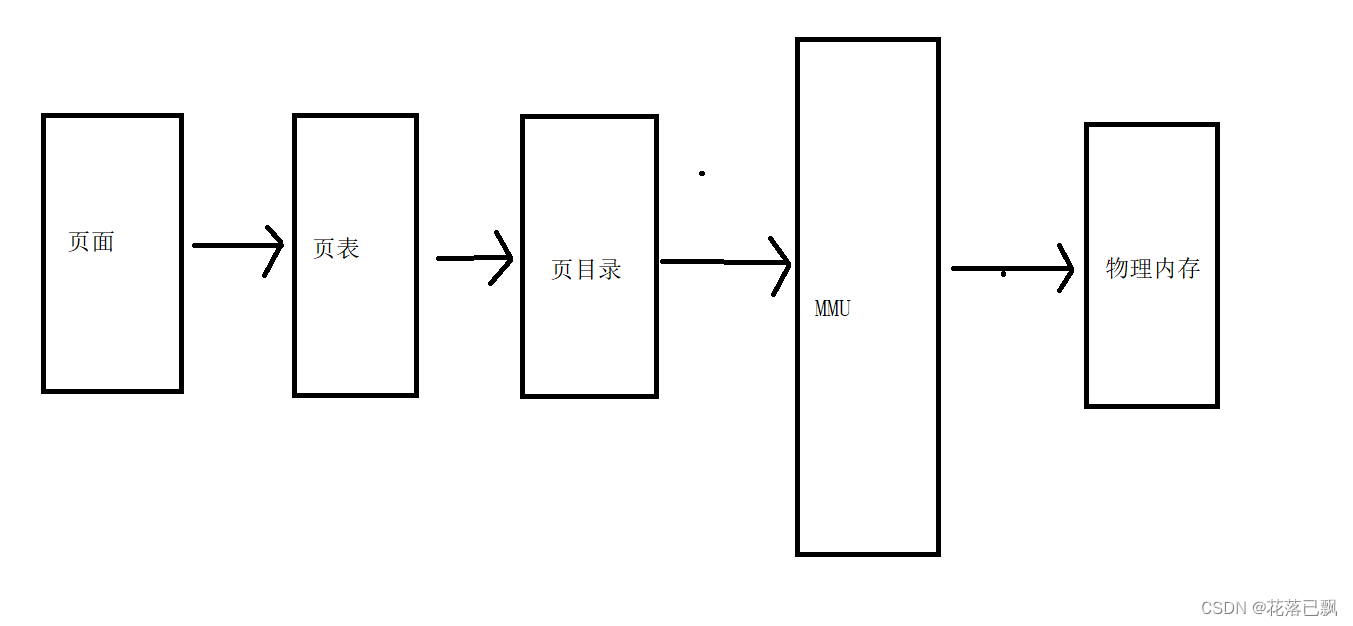
嵌入式面试笔试刷题(day14)
文章目录 前言一、进程控制块1.PCB控制块的作用2.PCB的存储位置 二、进程的三级映射三、return , exit, pthread_exit四、pthread_join作用五、互斥锁和信号量的区别六、怎么判断链表是否有环总结 前言 本篇文章继续我们的刷题之路。 一、进程控制块 这里只讲解进程的PCB控制…...
好用免费的Chat GPT(亲测有用)
1、MindLink麦灵 MindLink麦灵 点进登录后 普通用户可以提问100次 2、你问我答 你问我答 无限次数的。 3、灵感 灵感 点击链接后会提示你如何下载使用。 这个有win版和mac版,点击登陆后,每日都会有30次GPT3/3.5的提问。 4、WebTab 在浏览器插件中…...
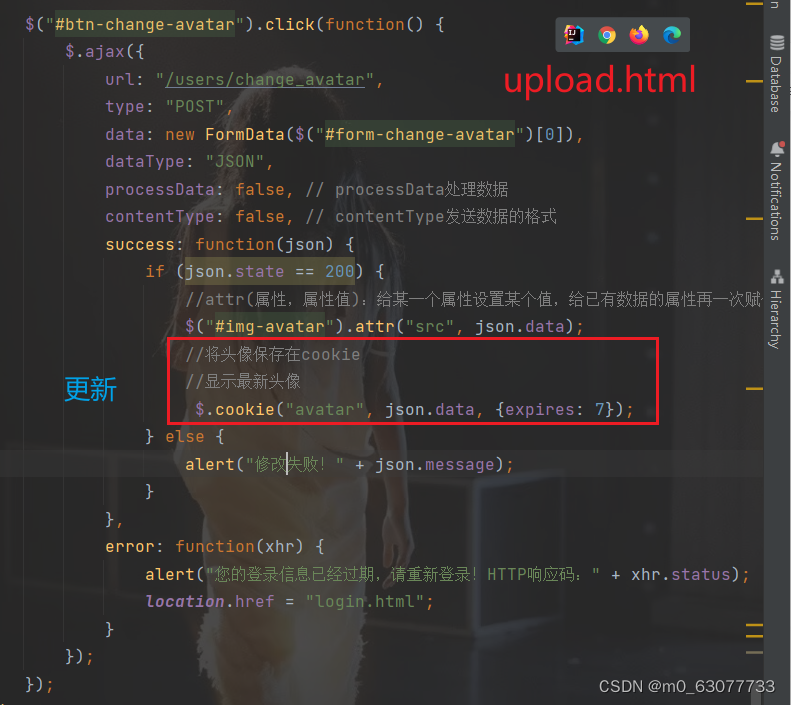
SpringBoot项目--电脑商城【上传头像】
一、易错点 1.错误写法: 把文件存到数据库中,需要图片时访问数据库,数据库将文件解析为字节流返回,最后写到本地的某一个文件.这种方法太耗费资源和时间了 2.正确写法: 将对应的文件保存在操作系统上,然后再把这个文件路径记录下来,因为在记录路径的…...

优化SOCKS5的方法
在今天的互联网世界中,保护个人隐私和提升网络速度至关重要。作为一种常用的代理协议,SOCKS5代理服务器不仅可以保护您的隐私,还可以实现更快速的网络访问。本文将为您介绍一些优化SOCKS5代理服务器的方法,以提高网络速度和安全性…...

使用 HelpLook Chatbot,让AI聊天机器人变成销售经理
想要增强AI聊天机器人销售技巧的话,我们需要一个强大的搭建工具来帮助我们增加客户互动,通过很多的客户互动数据来支撑和锻炼我们的AI聊天机器人。在本篇文章中,looklook将会系统地来说说该如何定制聊天机器人的行为。 使用AI聊天机器人的好处…...
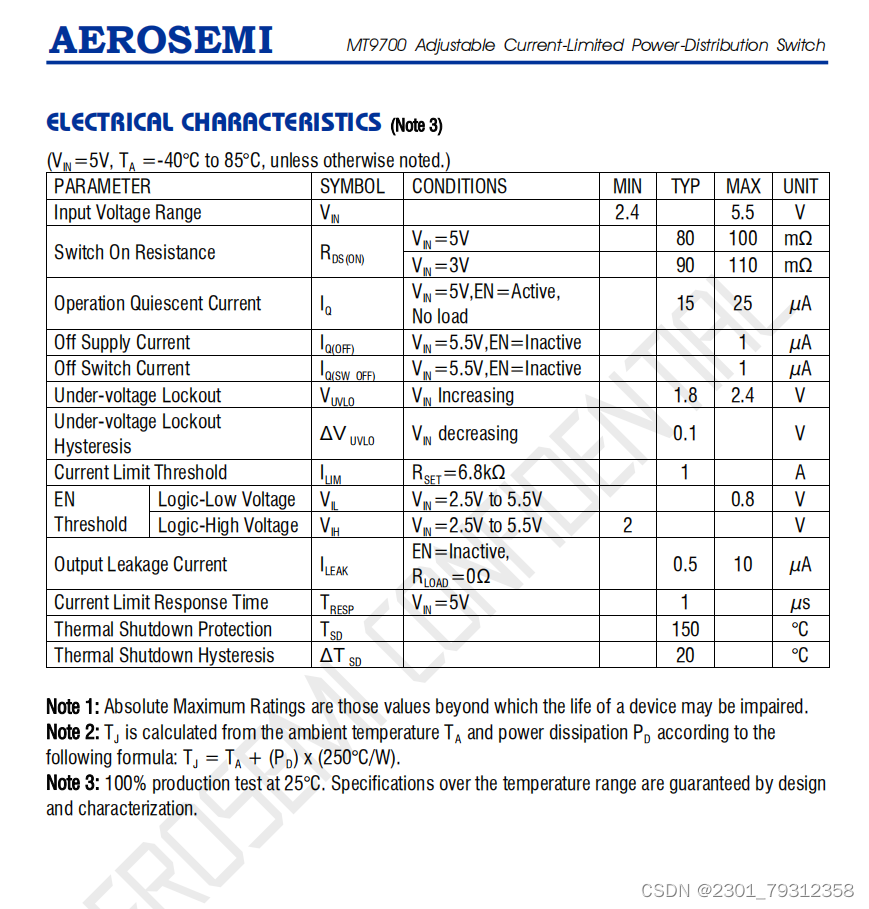
MT9700 80mΩ,可调快速响应限流配电开关芯片
MT9700 80mΩ,可调快速响应限流配电开关芯片 特征 符合USB规范 集成80mΩ电源MOSFET 低电源电流 15μA典型开启状态 1μA典型关闭状态 宽输入电压Range:2.4V到5.5V 快速瞬态响应:<2μs 反向电流流阻塞 热关机保护 热插件应…...

RabbitMQ之延迟队列
RabbitMQ之延迟队列 1. 延迟队列概念2. 延迟队列使用场景3. RabbitMQ 中的 TTL3.1 消息设置 TTL3.2 队列设置 TTL3.3 两者的区别 4. 整合 SpringBoot4.1 创建项目4.2 添加依赖4.3 修改配置文件4.4 添加 Swagger 配置类 5. 队列 TTL5.1 代码架构图5.2 配置文件类代码5.3 消息生产…...

k8s部署手册-v06
一、基础配置 1.修改主机名 hostnamectl set-hostname k8s-master01 hostnamectl set-hostname k8s-master02 hostnamectl set-hostname k8s-master03 hostnamectl set-hostname k8s-node01 hostnamectl set-hostname k8s-node022.添加 主机名与IP地址解析 cat > /etc/ho…...

Qt 5.15集成Crypto++ 8.7.0(MSVC 2019)笔记
一、背景 笔者已介绍过在Qt 5.15.x中使用MinGW(8.10版本)编译并集成Crypto 8.7.0。 但是该编译出来的库(.a和.dll)不适用MSVC(2019版本)构建环境,需要重新编译(.lib或和.dll…...
)
LeetCode——贪心篇(一)
刷题顺序及思路来源于代码随想录,网站地址:https://programmercarl.com 目录 455. 分发饼干 376. 摆动序列 53. 最大子数组和 122. 买卖股票的最佳时机 II 55. 跳跃游戏 45. 跳跃游戏 II 1005. K 次取反后最大化的数组和 455. 分发饼干 假设你是…...

2023高教社杯 国赛数学建模C题思路 - 蔬菜类商品的自动定价与补货决策
1 赛题 在生鲜商超中,一般蔬菜类商品的保鲜期都比较短,且品相随销售时间的增加而变差, 大部分品种如当日未售出,隔日就无法再售。因此, 商超通常会根据各商品的历史销售和需 求情况每天进行补货。 由于商超销售的蔬菜…...
线性运算的推广与矩阵基础)
【理解线性代数】(四)线性运算的推广与矩阵基础
1. 数值加法和乘法 数值加法与乘法,是小学数学课程中的基本数学运算。例如: 加法:112 乘法:2*24 在这个知识层次下,运算的基本单位是数字。 2. 从数值到向量 数值加法,可以看作一维空间中的向量加法&…...

C# 什么是继承和派生
C# 什么是继承和派生 在 C# 中,继承(Inheritance)是一种机制,它允许一个类(子类)从另一个类(父类)中继承属性和方法。这种关系使得子类可以重用父类的代码,同时可以在子…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
