算法笔记:堆
【如无特别说明,皆为最小二叉堆】
1 介绍

2 特性
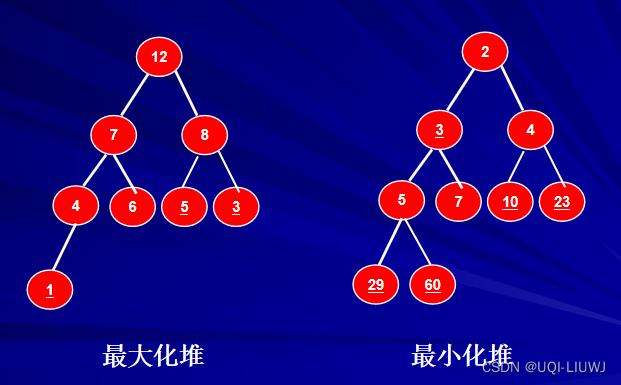
- 结构性:符合完全二叉树的结构
- 有序性:满足父节点小于子节点(最小化堆)或父节点大于子节点(最大化堆)
3 二叉堆的存储
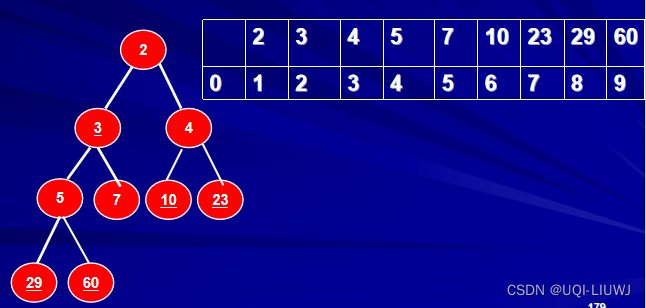
顺序存储
二叉堆的有序性可以很容易地通过下标来反映
4 堆中插入新元素
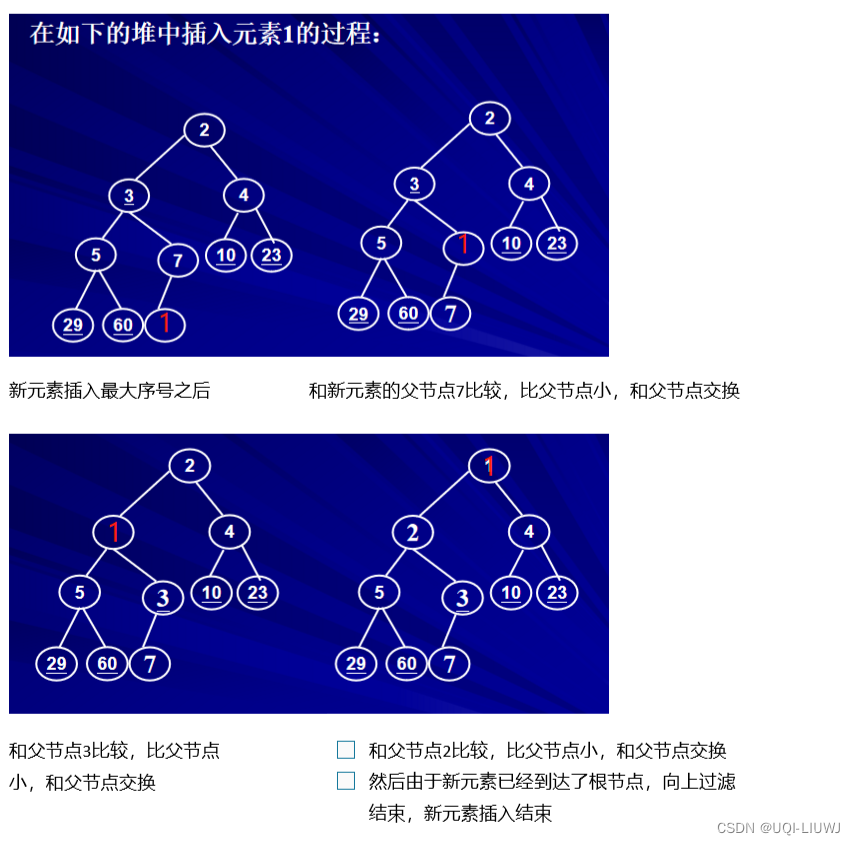
- 堆的插入是在具有最大序号的元素之后插入新的元素或结点,否则将违反堆的结构性。
- 如果新元素放入后,没有违反堆的有序性,那么操作结束。
- 否则,让该节点向父节点移动,直到满足有序性或到达根节点。
- 新节点的向上移动称为向上过滤
4.1 时间效率
- 最坏情况是O(logn) 【一直交换到根节点】
- 平均情况,过滤会提前结束。
- 有资料表明,平均是2.6次比较,因此元素平均上移1.6层。
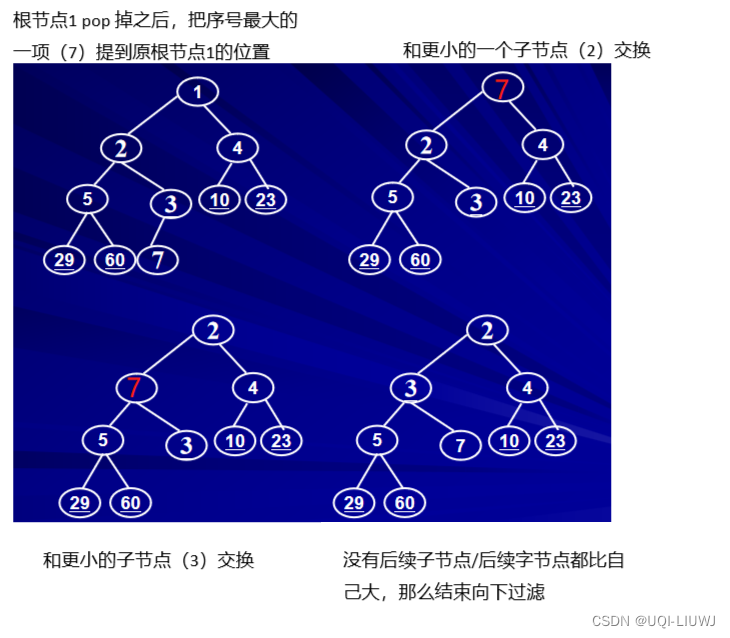
5 推出操作(DeQueue)
- 当最小元素被删除时,在根上出现了一个空结点。堆的大小比以前小1,堆的结构性告诉我们,最后一个结点应该删掉。
- 如果最后一项可以放在此空结点中,就把它放进去。然而,这通常是不可能的
- 必须玩与插入操作类似的“游戏”:把某些项放入空结点,然后移动空结点。
- 仅有的区别在于:对DeQueue操作,空结点是往下移动。
- 找到空结点的一个较小的子结点,如果该儿子的值小于我们要放入的项,则把该儿子放入空结点,把空结点往下推一层
- 重复这个动作,直到该项能被放入正确的位置。
5.1 时间复杂度
- 最坏情况下,deQueue是一个对数时间的操作
- 根据堆的有序性,堆中最后一个结点的值一般都是比较大的。因此,向下过滤很少有提前一或二层结束的,所以deQueue操作平均也是对数时间
6 建堆
- 可以看成N次连续插入,其时间应该是在O(NlogN)时间内完成
- 事实上,在构造过程中,我们并不关心每个元素加入后堆的状态,我们关心的是N个元素全部加入后的最后状态,最后的状态是要保证堆的有序性。至于中间过程中的有序性是否成立并不重要。
- 有了这个前提后,我们能将构造堆的时间复杂度降到O(N)
- 利用堆的递归定义
- 如果函数buildHeap可以将一棵完全二叉树调整为一个堆 ,那么,只要对左子堆和右子堆递归调用buildHeap。
- 至此,我们能保证除了根结点外,其余的地方都建立起了堆的有序性。
- 然后对根结点调用向下过滤,以创建堆的有序性
- 如果我们以逆向层次的次序对结点调用向下过滤,那么在向下过滤节点i时,所有结点i的子孙都已经调用过向下过滤。
- 不需要对叶结点执行向下过滤
- 从编号最大的非叶结点开始向下过滤
- 利用堆的递归定义
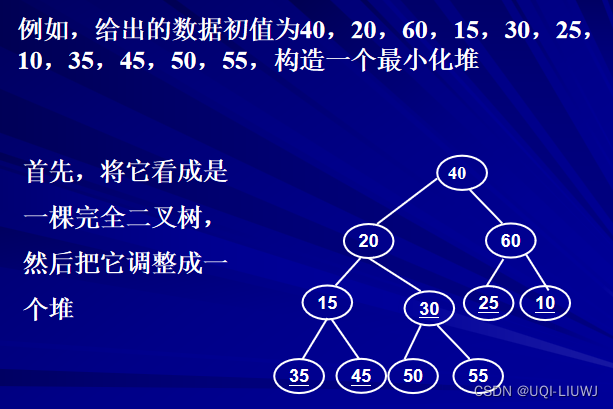
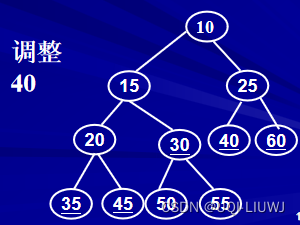
6.1 举例
一开始根据数据的先后建立一棵完全二叉树
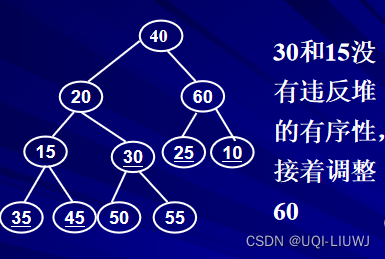
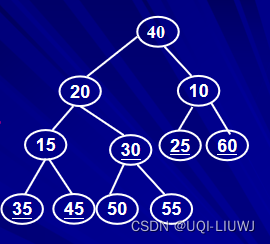
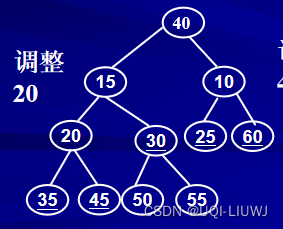
从序号最大的非叶子节点(30)开始进行向下过滤
6.2 时间分析
- 为h的节点(叶节点高度为0),在向下过滤中交换的最大次数是h
- 建堆的最大时间是所有节点的调整时所需交换次数之和,即所有节点的高度之和

7 D堆
- 每个节点有d个儿子,这样生成的堆比较矮。
- 插入:
- 删除:需要在d个元素中找出最小的,时间复杂度为:
- 优点:插入快
- 缺点:删除慢
- 用途:
- 插入比删除多的队列
- 队列太大,内存放不下,要放在外存的时候
相关文章:
算法笔记:堆
【如无特别说明,皆为最小二叉堆】 1 介绍 2 特性 结构性:符合完全二叉树的结构有序性:满足父节点小于子节点(最小化堆)或父节点大于子节点(最大化堆) 3 二叉堆的存储 顺序存储 二叉堆的有序…...
vue3 判断包含某个字符
<img v-if"node.level 1 && checkIfIncludeSubStr(node.label, 人口)"src"/assets/images/icon-convention-01.png" width"16"class"inlineBlock Vmiddle" style"margin-right: 8px;"/>const data reactive…...

MySQL的故事——查询性能优化
查询性能优化 文章目录 查询性能优化一、查询优化器的提示(hint)二、优化特定类型的查询 一、查询优化器的提示(hint) HIGH_PRIORITY和LOW_PRIORITY 这个提示告诉MySQL,当多个语句同时访问某一个表时,哪些语句的优先级相对高些,哪些相对低些…...
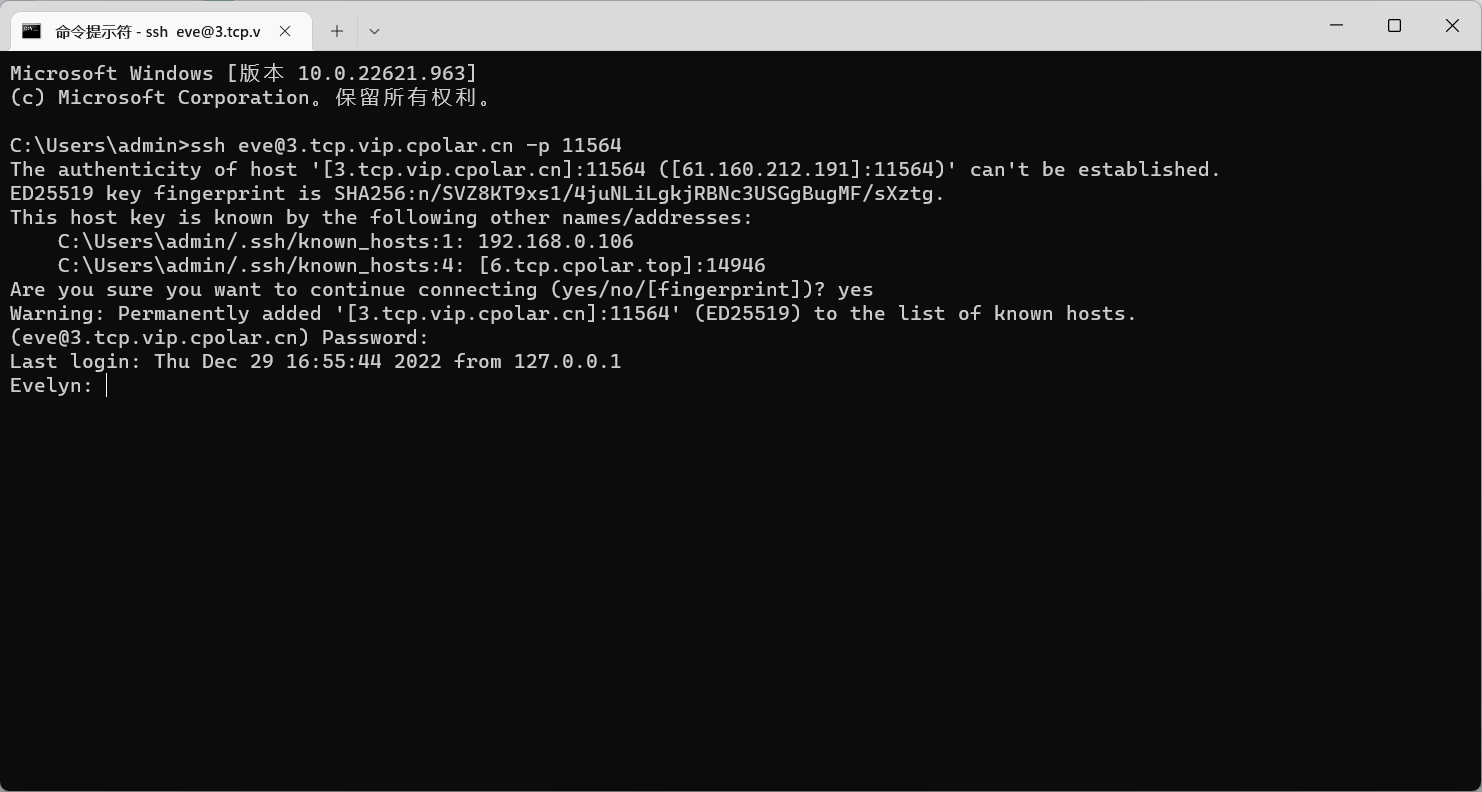
在外SSH远程连接macOS服务器【cpolar内网穿透】
文章目录 前言1. macOS打开远程登录2. 局域网内测试ssh远程3. 公网ssh远程连接macOS3.1 macOS安装配置cpolar3.2 获取ssh隧道公网地址3.3 测试公网ssh远程连接macOS 4. 配置公网固定TCP地址4.1 保留一个固定TCP端口地址4.2 配置固定TCP端口地址 5. 使用固定TCP端口地址ssh远程 …...

Nosql数据库服务之redis
Nosql数据库服务之redis 一图详解DB的分支产品 Nosql数据库介绍 是一种非关系型数据库服务,它能解决常规数据库的并发能力,比如传统的数据库的IO与性能的瓶颈,同样它是关系型数据库的一个补充,有着比较好的高效率与高性能。 专…...

当AI遇到IoT:开启智能生活的无限可能
文章目录 1. AI和IoT的融合1.1 什么是人工智能(AI)?1.2 什么是物联网(IoT)?1.3 AI和IoT的融合 2. 智能家居2.1 智能家居安全2.2 智能家居自动化 3. 医疗保健3.1 远程监护3.2 个性化医疗 4. 智能交通4.1 交通…...
Qt5界面Qt Designer上添加资源图片后,ModuleNotFoundError: No module named ‘rcc_rc‘ 的终极解决方案
在网上找了很久都没弄明白,最后还是自己思考解决了。 起因: 用 Qt Designer 添加资源文件作为背景图,编译 \resource\static\qrc> pyuic5 -o .\xx.py .\xx.ui发现在 xx.py 文件末尾中多了一个语句: import rcc_rc然后运行就…...

社群运营怎么做?
社区运营虽然说起来简单,可是实际执行起来却常常发现无从下手。刑天营销曾经做过社区运营的案子,我们也总结一套自己的方法,要做好社群运营,以下的这些问题就不能忽视: 一、做好社区定位 做社区运营,首先…...
Vite,Vue3项目引入dataV报错的解决方法
背景:开发一个大屏项目中,需要是要DataV的那边边框,装饰等,只是DataV是基于vue2的,vue3版的作者还在开发中,于是翻了DataV的源码,发现使用esm方式时是直接引入源码而不经过打包,其源码中使用的vue语法vue3也支持,所以可以直接在vue3中引入使用. vite,vue3项目直接引入DataV 安…...
QT(8.30)常用类与组件,实现登录界面
1.作业: 完成一个登录界面(图片未附带): 头文件: #ifndef WIDGET_H #define WIDGET_H#include <QWidget>#include <QLineEdit>//行编辑器#include<QIcon>//图标#include<QLabel>//标签#include<QPushButton>//按钮#include<QIc…...

【Two Stream network (Tsn)】(二) 阅读笔记
贡献 将深度神经网络应用于视频动作识别的难点,是如何同时利用好静止图像上的 appearance information以及物体之间的运动信息motion information。本文主要有三点贡献: 1.提出了一种融合时间流和空间流的双流网络; 2.证明了直接在光流上训…...

记一次语音播报功能
浏览器本身就可以读文字 写功能前一直以为该功能得调用第三方平台的API才可以文字合成语音后用音频播放,原来HTML5已经支持了该功能(TTS)了 SpeechSynthesis 和 SpeechSynthesisUtterance SpeechSynthesis SpeechSynthesisUtterance let …...
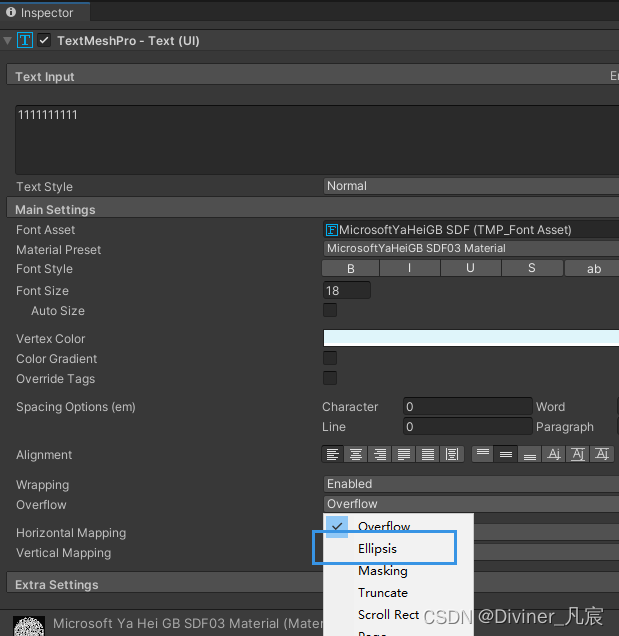
Unity设置TextMeshPro文本超出范围显示...
TextMtshPro文本超出范围,展示省略。选择Overflow为Ellipsis。...

Java中级面试题记录(三)
1.职业规划? 2.每家公司离职原因? 3.SpringCloud用到了哪些组件? GateWayNacosOpenFeignSeataHystrix 4.PG和Mysql的区别? 5.两种数据库的存储区别? 6.MySQL索引了解的内容? 一口气搞定索引的所有知识…...
)
spring高级源码50讲-1-8(spring容器与bean)
文章目录 容器与 bean1) 容器接口演示1 - BeanFactory 与 ApplicationContext 的区别关键代码参考 收获💡演示2 - 国际化 2) 容器实现演示1 - DefaultListableBeanFactory代码参考 收获💡演示2 - 常见 ApplicationContext 实现代码参考 收获💡…...
微服务06-Dockerfile自定义镜像+DockerCompose部署多个镜像
常见的镜像在DockerHub能找到,但是我们自己写项目得自己构造镜像 1 镜像结构 作用:提高复用性,当应用需要更新时,不再是整个系统重装进行更新 ,而是对需要更新的部分进行更新,其他地方不动——>这就是分…...

2023高教社杯 国赛数学建模A题思路 - 定日镜场的优化设计
1 赛题 A 题 定日镜场的优化设计 构建以新能源为主体的新型电力系统, 是我国实现“碳达峰”“碳中和”目标的一项重要 措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术[1]。 定日镜是塔式太阳能光热发电站(以下简称塔式电站)收集太阳能的基本组件&…...
Qt +VTK+Cmake 编译和环境配置(第二篇,中级篇, 重新编译)
1.下载VTK和Cmake 这里不介绍了。我的VTK 8.2.0 cmake 3.27.4 就是不服这编译器了。重新来一次 打开Cmake,把VTK源文件路径和目标路径设置一下(目标路径自己设置,随意) 点击Configure:。 点击下一步 选择好 Qt的gcc…...
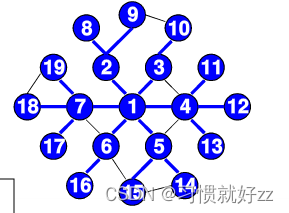
图的学习,深度和广度遍历
一、什么是图 表示“多对多”的关系 包括: 一组顶点:通常用V(Vertex)表示顶点集合一组边:通常用E(Edge)表示边的集合 边是顶点对:(v, w)∈E,其中v,w∈V有向边<v, w&…...

ChatGPT驱动下,网站AI客服该如何进步和创新
在ChatGPT这个AI智能的驱动下,网站AI客服在进步和创新方面有很多潜力。由于GPT模型的强大语言处理能力和智能对话技巧,使得网站AI客服能够更准确和流畅地与用户交互。looklook今天总结了一些网站AI客服智能的进步和创新方向,以供大家参考。 网…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...