图的学习,深度和广度遍历
一、什么是图
表示“多对多”的关系
包括:
- 一组顶点:通常用V(Vertex)表示顶点集合
- 一组边:通常用E(Edge)表示边的集合
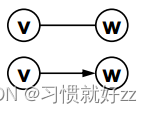
- 边是顶点对:(v, w)∈E,其中v,w∈V
- 有向边<v, w>表示从v指向w的边(单行线)
- 不考虑重边和自回路
二、抽象数据类型定义
- 类型名称:图(Graph)
- 数据对象集:G(V, E)由一个非空的有限顶点集合v和一个有限边集合E组成。
- 操作集:对于任意图G ∈ Graph, 以及v ∈ V, e ∈ E
- Graph Create():建立并返回空图;
- Graph InsertVertex(Graph G, Vertex v):将v插入G;
- Graph InsertEdge(Graph G, Edge e):将e插入G;
- void DFS(Graph G, Vertex v):从顶点v出发深度优先遍历图G;
- void BFS(Graph G, Vertex v):从顶点v触发宽度优先遍历图G;
- void ShortestPath(Graph G, Vertex v, int Dist[]):计算图G中顶点v到任一其他顶点的最短距离;
- void MST(Graph G):计算图G的最小生成树;
- …
- 数据结构中对于稀疏图的定义为:有很少条边或弧(边的条数|E|远小于|V|²)的图称为稀疏图(sparse graph),反之边的条数|E|接近|V|²,称为稠密图(dense graph)。
如何表示图:

/* 图的邻接矩阵表示法 */#define MaxVertexNum 100 /* 最大顶点数设为100 */#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/typedef int Vertex; /* 用顶点下标表示顶点,为整型 */typedef int WeightType; /* 边的权值设为整型 */typedef char DataType; /* 顶点存储的数据类型设为字符型 *//* 边的定义 */typedef struct ENode *PtrToENode;struct ENode{Vertex V1, V2; /* 有向边<V1, V2> */WeightType Weight; /* 权重 */};typedef PtrToENode Edge;/* 图结点的定义 */typedef struct GNode *PtrToGNode;struct GNode{int Nv; /* 顶点数 */int Ne; /* 边数 */WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */DataType Data[MaxVertexNum]; /* 存顶点的数据 *//* 注意:很多情况下,顶点无数据,此时Data[]可以不用出现 */};typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */MGraph CreateGraph( int VertexNum ){ /* 初始化一个有VertexNum个顶点但没有边的图 */Vertex V, W;MGraph Graph;Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */Graph->Nv = VertexNum;Graph->Ne = 0;/* 初始化邻接矩阵 *//* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */for (V=0; V<Graph->Nv; V++)for (W=0; W<Graph->Nv; W++) Graph->G[V][W] = INFINITY;return Graph; }void InsertEdge( MGraph Graph, Edge E ){/* 插入边 <V1, V2> */Graph->G[E->V1][E->V2] = E->Weight; /* 若是无向图,还要插入边<V2, V1> */Graph->G[E->V2][E->V1] = E->Weight;}MGraph BuildGraph(){MGraph Graph;Edge E;Vertex V;int Nv, i;scanf("%d", &Nv); /* 读入顶点个数 */Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ scanf("%d", &(Graph->Ne)); /* 读入边数 */if ( Graph->Ne != 0 ) { /* 如果有边 */ E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */ /* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */for (i=0; i<Graph->Ne; i++) {scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); /* 注意:如果权重不是整型,Weight的读入格式要改 */InsertEdge( Graph, E );}} /* 如果顶点有数据的话,读入数据 */for (V=0; V<Graph->Nv; V++) scanf(" %c", &(Graph->Data[V]));return Graph;}
领接表:G[N]为指针数组,对应矩阵每行一个链表,只存非0元素。
对于网络,结构中要增加权重的域。
/* 图的邻接表表示法 */#define MaxVertexNum 100 /* 最大顶点数设为100 */typedef int Vertex; /* 用顶点下标表示顶点,为整型 */typedef int WeightType; /* 边的权值设为整型 */typedef char DataType; /* 顶点存储的数据类型设为字符型 *//* 边的定义 */typedef struct ENode *PtrToENode;struct ENode{Vertex V1, V2; /* 有向边<V1, V2> */WeightType Weight; /* 权重 */};typedef PtrToENode Edge;/* 邻接点的定义 */typedef struct AdjVNode *PtrToAdjVNode; struct AdjVNode{Vertex AdjV; /* 邻接点下标 */WeightType Weight; /* 边权重 */PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */};/* 顶点表头结点的定义 */typedef struct Vnode{PtrToAdjVNode FirstEdge;/* 边表头指针 */DataType Data; /* 存顶点的数据 *//* 注意:很多情况下,顶点无数据,此时Data可以不用出现 */} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 *//* 图结点的定义 */typedef struct GNode *PtrToGNode;struct GNode{ int Nv; /* 顶点数 */int Ne; /* 边数 */AdjList G; /* 邻接表 */};typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */LGraph CreateGraph( int VertexNum ){ /* 初始化一个有VertexNum个顶点但没有边的图 */Vertex V;LGraph Graph;Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */Graph->Nv = VertexNum;Graph->Ne = 0;/* 初始化邻接表头指针 *//* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */for (V=0; V<Graph->Nv; V++)Graph->G[V].FirstEdge = NULL;return Graph; }void InsertEdge( LGraph Graph, Edge E ){PtrToAdjVNode NewNode;/* 插入边 <V1, V2> *//* 为V2建立新的邻接点 */NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));NewNode->AdjV = E->V2;NewNode->Weight = E->Weight;/* 将V2插入V1的表头 */NewNode->Next = Graph->G[E->V1].FirstEdge;Graph->G[E->V1].FirstEdge = NewNode;/* 若是无向图,还要插入边 <V2, V1> *//* 为V1建立新的邻接点 */NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));NewNode->AdjV = E->V1;NewNode->Weight = E->Weight;/* 将V1插入V2的表头 */NewNode->Next = Graph->G[E->V2].FirstEdge;Graph->G[E->V2].FirstEdge = NewNode;}LGraph BuildGraph(){LGraph Graph;Edge E;Vertex V;int Nv, i;scanf("%d", &Nv); /* 读入顶点个数 */Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ scanf("%d", &(Graph->Ne)); /* 读入边数 */if ( Graph->Ne != 0 ) { /* 如果有边 */ E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */ /* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */for (i=0; i<Graph->Ne; i++) {scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); /* 注意:如果权重不是整型,Weight的读入格式要改 */InsertEdge( Graph, E );}} /* 如果顶点有数据的话,读入数据 */for (V=0; V<Graph->Nv; V++) scanf(" %c", &(Graph->G[V].Data));return Graph;}
其中
typedef struct Vnode{PtrToAdjVNode FirstEdge;/* 边表头指针 */DataType Data; /* 存顶点的数据 *//* 注意:很多情况下,顶点无数据,此时Data可以不用出现 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 *///AdjList是一个Vnode为元素的数组的别名
图的度是和顶点相关联的边的数目
三、图的遍历
3.1 深度优先算法
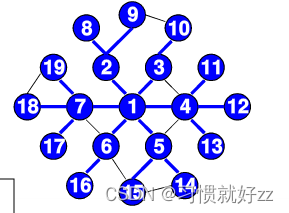
邻接表
/* 邻接表存储的图 - DFS*/void Visit(Vertex V)
{printf("Now visit Vertex %d\n", V);
}/* Visited[]为全局变量,已经初始化false */
void DFS(LGraph Graph, Vertex V, void (*Visit)(Vertex))
{ /* 以V为出发点对邻接表存储的图Graph进行DFS搜索 */PtrToAdjVNode W;Visit(V); /* 访问第V个顶点 */Visited[V] = true; /* 标记V已访问 */for(W=Graph->G[V].FirstEdge;W;W=W->Next) /* 对V的每个邻接点W->AdjV */if(!Visited[W->AdjV]) /* 若W->AdjV未被访问 */DFS(Graph, W->AdjV, Visit); /* 则递归访问之 */
}
邻接矩阵
void Visit(Vertex V)
{printf("Now visit Vertex %d\n", V);
}void DFS(MGraph Graph, Vertex V, int *Visited)
{Vertex W;Visit(V);Visited[V] = 1; //已访问for(W=0;W<Graph->Nv;W++)if(Graph->G[V][W]==1 && Visited[W]==0)DFS(Graph, W, Visited);
}
3.2 广度优先算法
邻接矩阵
/* 邻接矩阵存储的图 - BFS *//* IsEdge(Graph, V, W)检查<V, W>是否图Graph中的一条边,即W是否V的邻接点 */
/* 此函数根据图的不同类型要做不同的实现,关键取决于对不存在的边的表示方法 */
/* 例如对有权图,如果不存在的边被初始化为INFINITY,则函数实现如下: */
bool IsEdge(MGraph Graph, Vertex V, Vertex W)
{return Graph->G[V][W]<INFINITY?true:false;
}/* Visited[]为全局变量,已经初始化为false */
void BFS(MGraph Graph, Vertex S, void(*Visit)(Vertex))
{ /* 以S为出发点对邻接矩阵存储的图Graph进行BFS搜索 */Queue Q;Vertex V, W;Q = CreateQueue(MaxSize); /* 创建空队列,MaxSize为外部定义的常数 *//* 访问顶点S:此处可根据具体访问需要改写 */Visit(S);Visited[S] = true; /* 标记S已访问 */AddQ(Q, S); /* S入对列 */while(!IsEmpty(Q)) {V = DeleteQ(Q); /* 弹出V */for(W=0;W<Graph->Nv;W++) /* 对图中的每个顶点W *//* 若W是V的邻接点并且未访问过 */if(!Visited[W] && IsEdge(Graph, V, W)) {/* 访问顶点W */Visist(W);Visited[W] = true; /* 标记W已访问 */AddQ(Q, W); /* W入队列 */}} /* while结束 */
}
相关文章:

图的学习,深度和广度遍历
一、什么是图 表示“多对多”的关系 包括: 一组顶点:通常用V(Vertex)表示顶点集合一组边:通常用E(Edge)表示边的集合 边是顶点对:(v, w)∈E,其中v,w∈V有向边<v, w&…...

ChatGPT驱动下,网站AI客服该如何进步和创新
在ChatGPT这个AI智能的驱动下,网站AI客服在进步和创新方面有很多潜力。由于GPT模型的强大语言处理能力和智能对话技巧,使得网站AI客服能够更准确和流畅地与用户交互。looklook今天总结了一些网站AI客服智能的进步和创新方向,以供大家参考。 网…...
Linux系统中实现便捷运维管理和远程访问的1Panel部署方法解析
文章目录 前言 前言 1Panel 是一个现代化、开源的 Linux 服务器运维管理面板。高效管理,通过 Web 端轻松管理 Linux 服务器,包括主机监控、文件管理、数据库管理、容器管理等下面我们介绍在Linux 本地安装1Panel 并结合cpolar 内网穿透工具实现远程访问1Panel 管理…...

数学建模黄河水沙监测数据分析
数学建模黄河水沙监测数据分析 问题: 黄河是中华民族的母亲河。研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变化和人民生活的影响,以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾等方面都具有重要的理论指导意义。 解题思…...
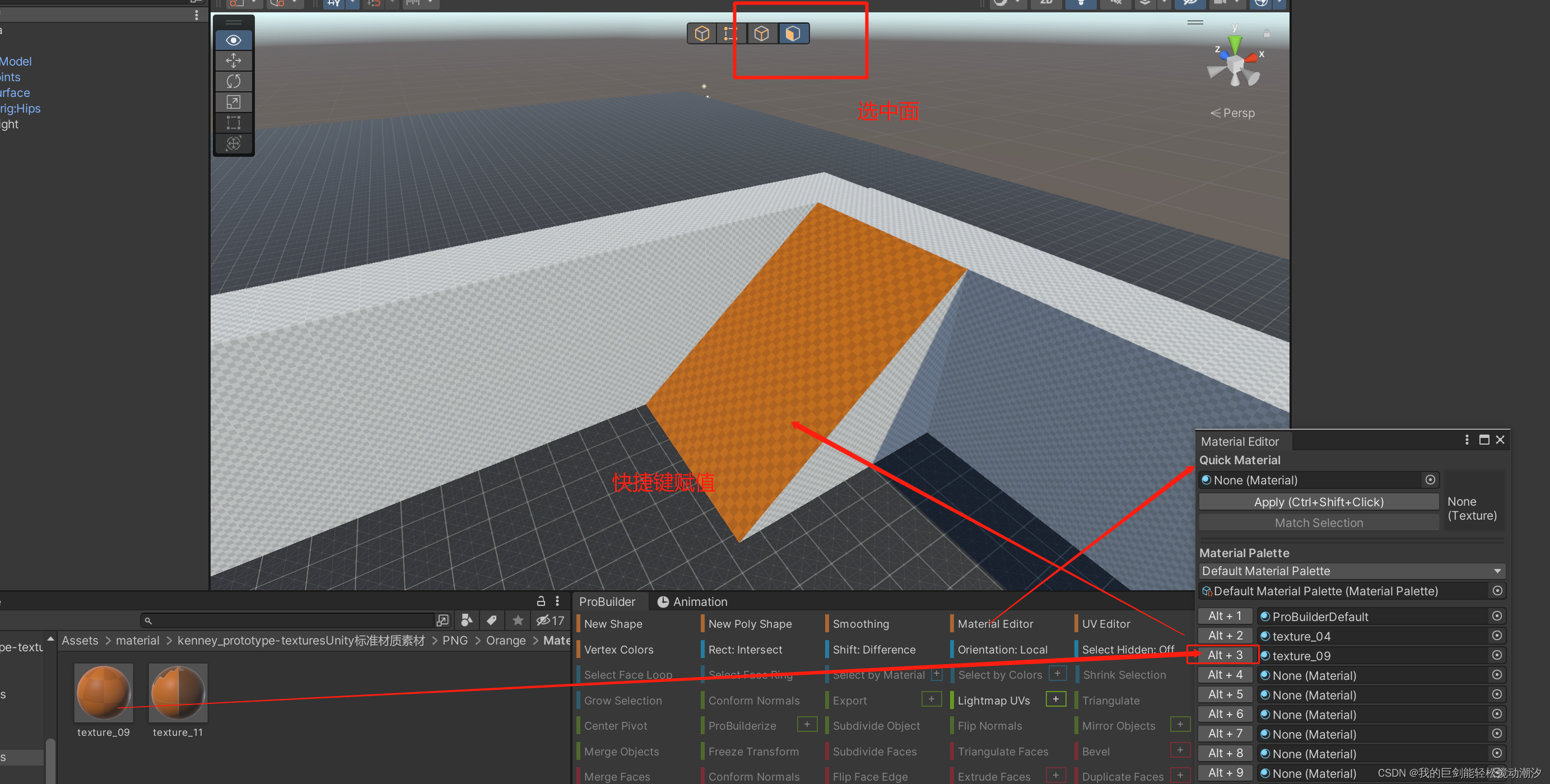
Unity ProBuilder(自己创建斜面、拐角)
目录 基础操作 下载 打开面板 新增对象 材质保存 1.斜面实例 2.拐角实例 3.切割实例 4.单独面赋值 基础操作 下载 打开面板 新增对象 选中想创建的块体后,在编辑器见面拉出块体 材质保存 打开材质编辑器后,将材质赋值,之后&am…...
以气象行业为例,浅谈在ToB/ToG行业中如何做好UI设计
商业气象公司是典型的TOB/TOG性质的公司,客户包括农业、能源、航空航天、交通运输、建筑工程等行业,它们需要准确的气象数据、预报和分析来支持业务决策和运营管理。商业气象公司通常会提供各种气象服务,如气象数据采集与分析、预报产品、风险…...

shiny根据数据的长度设置多个色板
shiny根据数据的长度设置多个色板 library(shiny) library(colourpicker) ui <- fluidPage(# 添加一个选择颜色的下拉菜单uiOutput("color_dropdown") )server <- function(input, output) {# 数据长度data_length <- reactive({length(c("数据1"…...

2023高教社杯 国赛数学建模D题思路 - 圈养湖羊的空间利用率
1 赛题 D 题 圈养湖羊的空间利用率 规模化的圈养养殖场通常根据牲畜的性别和生长阶段分群饲养, 适应不同种类、不同阶段 的牲畜对空间的不同要求,以保障牲畜安全和健康;与此同时,也要尽量减少空间闲置所造成 的资源浪费。在实际…...
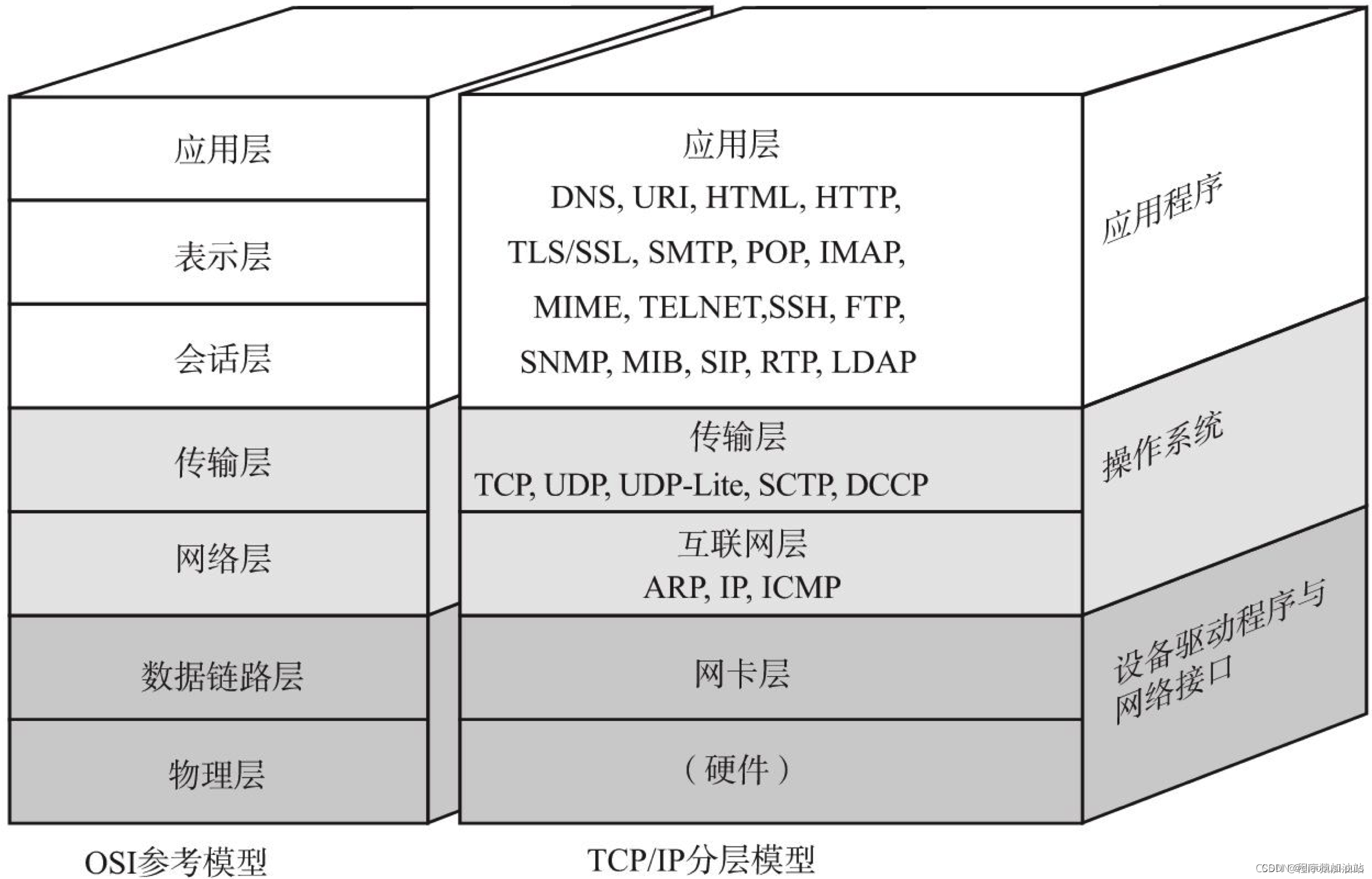
网络是如何进行通信
网络是如何进行通信的 简介 在现代社会中,网络已经成为我们生活中不可或缺的一部分。从上网搜索信息、在线购物到远程工作和社交媒体,我们几乎无时无刻不与网络保持着联系。但是,网络究竟是个什么玩意,它是如何工作的呢…...

vue3 watch watchEffect
watch & watchEffect 函数都是监听器, 用于监视数据的变化; watch 有惰性,watchEffect 无惰性;watch 需要指定具体的监视属性,watchEffect 不需要指定具体的监视属性和配置参数,会自动感知代码依赖;watch 能获取到…...

lintcode 1410 · 矩阵注水【BFS 中等 vip】
题目链接,描述 https://www.lintcode.com/problem/1410 给一个二维矩阵,每个grid的值代表地势的高度。水流只会沿上下左右流动,且必须从地势高的地方流向地势低的地方。视为矩阵四面环水,现在从(R,C)处注水,问水能否…...
 架构评估(复审)-方法论)
软件架构设计(十) 架构评估(复审)-方法论
我们上一节讲到了为什么么要进行架构的评估, 以及架构评估有哪些质量属性,本节正式来学习架构评估的一些方法论。 再讲到架构评估之前,还需要了解几个概念,也就是风险点,非风险点,敏感点,权衡点等。 风险点:系统架构风险是指架构设计中潜在的,存在问题的架构策略所带…...
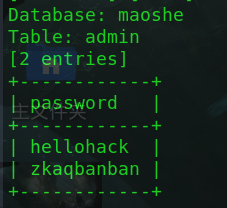
SQL注入案例
目录 一、简介 二、案例 1.发现注入点 2.寻找注入类型 3.寻找字段数 4.将传参值设为超出数据量的大值,联合查询找到回显位置 5.找到数据库 6.寻找库中的表 7.寻找表中列 8.查看表中数据 附:SQLMap注入 1.输入指令查数据库 2.输入指令查表 3…...

lv3 嵌入式开发-5 linux shell命令(进程管理、用户管理)
目录 1 进程处理相关命令 1.1 进程的概念 1.2 查看进程的命令 1.3 发送信号命令 2 用户管理相关命令 2.1 用户管理相关文件介绍 2.2 用户管理相关命令介绍 1 进程处理相关命令 1.1 进程的概念 进程的概念主要有两点: 进程是一个实体。每一个进程都有它自己…...

学习Bootstrap 5的第六天
目录 信息警告框 警告框 实例 警告框链接 实例 关闭警告框 实例 警告框动画 实例 按钮 按钮样式 实例 按钮轮廓 实例 编辑按钮尺寸 实例 块级按钮 实例 实例 活动/禁用按钮 实例 加载器按钮 实例 扩展小知识 按钮组 按钮组 实例 实例 垂直按钮组…...
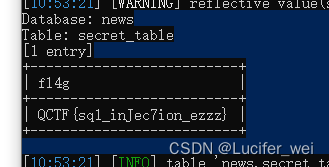
攻防世界-WEB-NewsCenter
打开环境 有查询,猜测是sql注入 保存请求头到文件中 准备利用sqlmap 查找数据库 python sqlmap.py -r ./123.txt --dbs 查找表 python sqlmap.py -r ./123.txt --tables -D news 查找字段 python sqlmap.py -r ./123.txt --column -D news -T secret_table 显示字…...

vue router 路由跳转获取不到参数
问题: 路由传参一直不能获取到参数, 未出现报错 原因: 混淆 query 和 params 的使用方法, 在使用 params 传参时错误的使用了 path 代码: 正确写法1: 使用path要对应query ...this.$router.push({path: /Health,query: {title:…...
将 Llama2 中文模型接入 FastGPT,再将 FastGPT 接入任意 GPT 套壳应用,真刺激!
FastGPT 是一个基于 LLM 大语言模型的知识库问答系统,提供开箱即用的数据处理、模型调用等能力。同时可以通过 Flow 可视化进行工作流编排,从而实现复杂的问答场景! Llama2 是Facebook 母公司 Meta 发布的开源可商用大模型,国内的…...
Ubuntu之apt-get系列--apt-get安装软件的方法/教程
原文网址:Ubuntu之apt-get系列--apt-get安装软件的方法/教程_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Ubuntu使用apt-get安装软件的方法。 安装软件 先更新列表 sudo apt-get update 安装软件 sudo apt-get install <package name>[<version>]…...

redux的理解
技术栈: react redux webpack react-router ES6/7/8 immutable 运行项目(nodejs 6.0) git clone https://github.com/bailicangdu/react-pxq.gitcd react-pxqnpm i 或者运行 yarn(推荐)npm startnpm run build (发布&…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
