JDK8增加的特性
Java知识点总结:想看的可以从这里进入
目录
- 13、JDK8增加的特性
- 13.1、Lambda表达式
- 13.2、方法的引用
- 13.3、时间处理类
- 13.4、接口增加方法
- 13.5、注解新增
- 13.6、Optional类
- 13.7、Stream
13、JDK8增加的特性
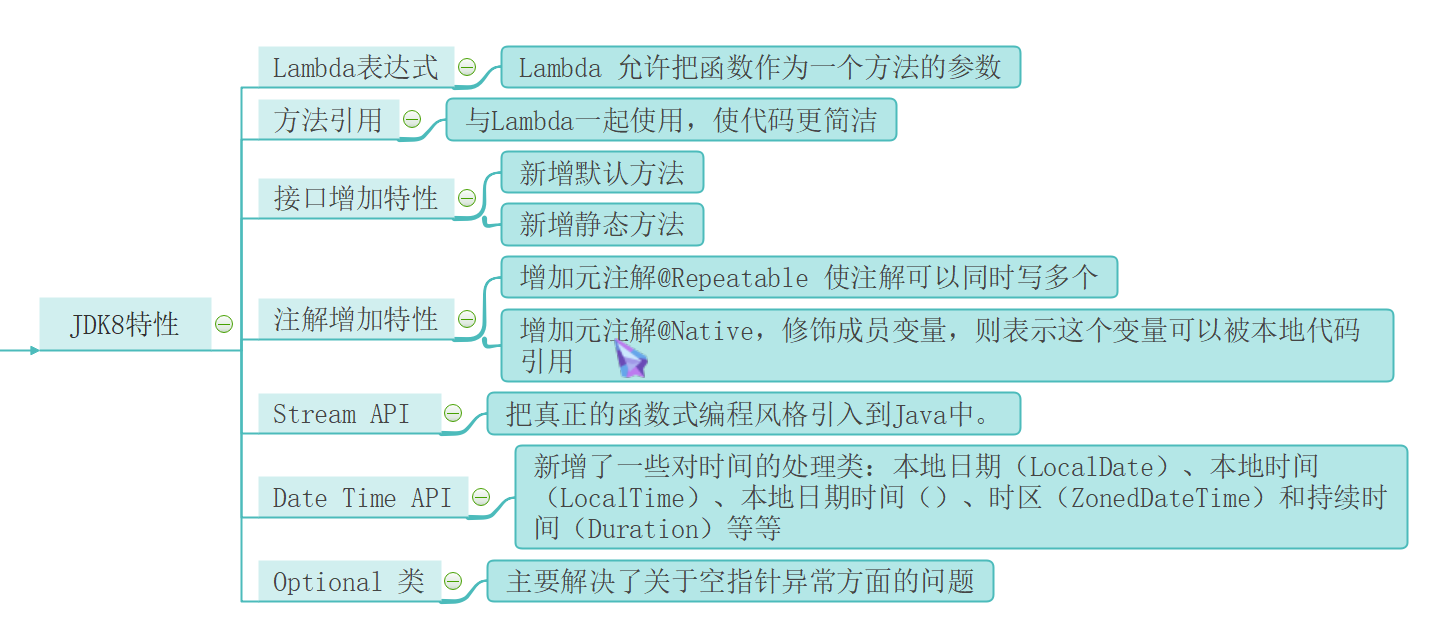
13.1、Lambda表达式
Lambda表达式和方法的引用
13.2、方法的引用
Lambda表达式和方法的引用
13.3、时间处理类
JDK8增加的时间处理类
13.4、接口增加方法
Java 8在接口中增加了默认方法与静态方法这两个新概念来扩展接口的声明。
接口的概念
13.5、注解新增
注解简介
Java 8引入了重复注解机制 @Repeatable ,可使相同的注解可以在同一地方声明多次。
Java 8扩展了注解的上下文,几乎可以为任何东西添加注解:局部变量、泛型类、父类与接口的实现,方法的异常等等。
13.6、Optional类
Optional类的使用 和 Stream流式操作
13.7、Stream
Optional类的使用 和 Stream流式操作
相关文章:

JDK8增加的特性
Java知识点总结:想看的可以从这里进入 目录13、JDK8增加的特性13.1、Lambda表达式13.2、方法的引用13.3、时间处理类13.4、接口增加方法13.5、注解新增13.6、Optional类13.7、Stream13、JDK8增加的特性 13.1、Lambda表达式 Lambda表达式和方法的引用 13.2、方法的…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 求数组中最大n个数和最小n个数的和(Python) | 机试题+算法思路+考点+代码解析 【2023】
求数组中最大n个数和最小n个数的和 给定一个数组,编写一个函数, 计算他的最大N个数和最小N个数的和, 需要对数组进行去重。 输入 第一行输入M,M表示数组大小 第二行输入M个数,表示数组内容 第三行输入N表示需要计算的最大最小N的个数 输出 输出最大N个数和最小N个数的…...

如何写出更加契合浙大MBA项目提面申请资料?
现在已经是2月中旬了,最近看到上海很多院校都已经公布了提前面批次相应时间了,等浙大复试工作结束,马上提前面批次时间也会出来。本人2023浙大提面也拿到了优秀,结合本人经验,今天给大家分享下申请材料该如何撰写&…...
)
华为OD机试真题Java实现【比赛评分】真题+解题思路+代码(20222023)
比赛评分 题目 一个有N个选手参加比赛,选手编号为1~N(3<=N<=100),有M(3<=M<=10)个评委对选手进行打分。打分规则为每个评委对选手打分,最高分10分,最低分1分。 请计算得分最多的3位选手的编号。如果得分相同,则得分高分值最多的选手排名靠前(10分数量相…...
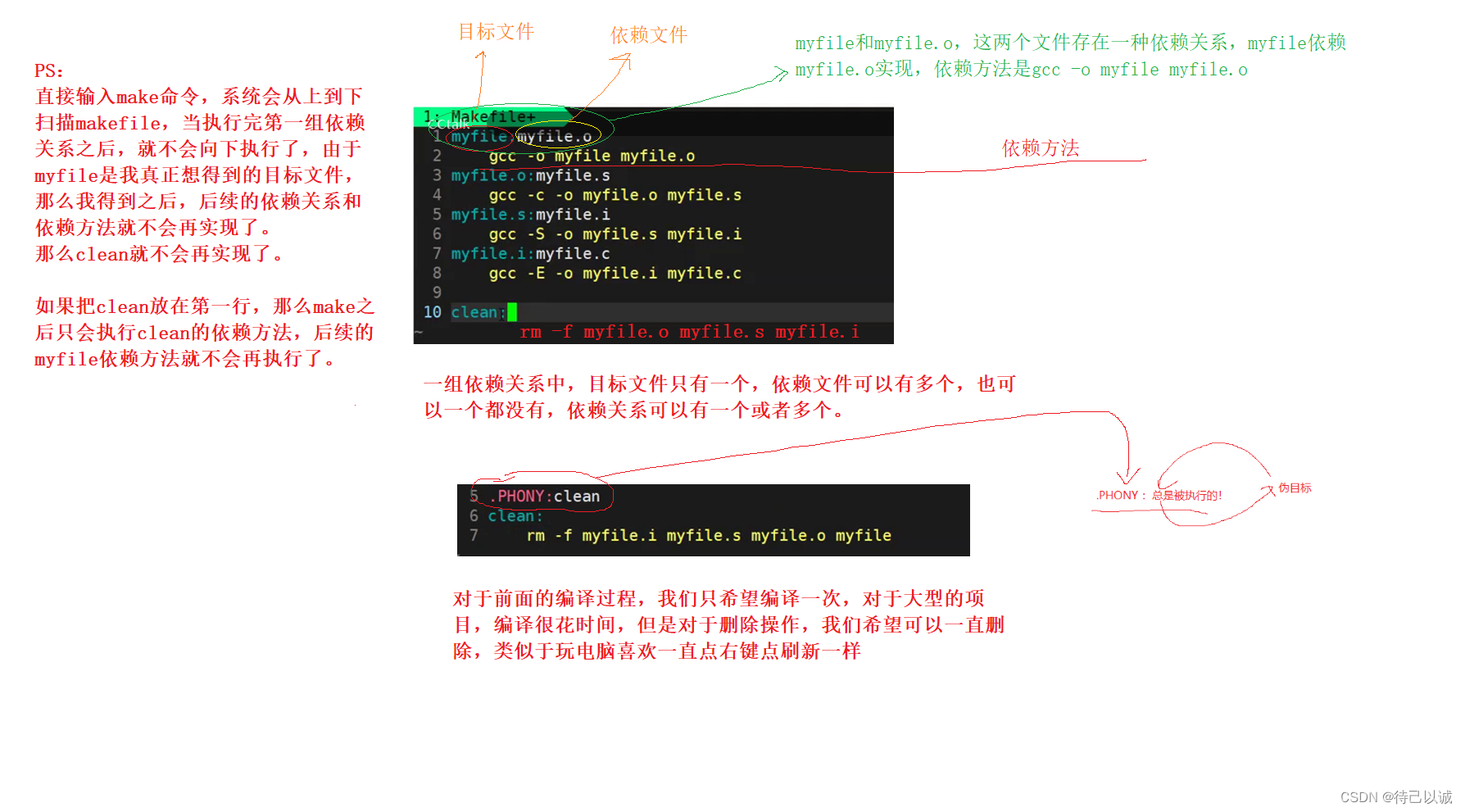
【linux】——gcc/g++,make/makefile的简单使用
目录 1.gcc的基本使用 2.Linux下的静态库和动态库的理解 3.Linux项目自动化构建工具——make/makefile 1.gcc的基本使用 gcc是专门用来编译c语言的 g是专门用来编译c的,但是g也能够用来编译c语言 预处理(进行宏替换) 预处理功能主要包括宏…...
追梦之旅【数据结构篇】——详解C语言动态实现带头结点的双向循环链表结构
详解C语言动态实现带头结点的双向循环链表结构~😎前言🙌预备小知识💞链表的概念及结构🙌预备小知识💞链表的概念及结构🙌带头结点的双向循环链表结构🙌整体实现内容分析💞1.头文件编…...
)
华为OD机试真题Python实现【水仙花数 2】真题+解题思路+代码(20222023)
水仙花数 2 题目 给定非空字符串 s,将该字符串分割成一些子串 使每个子串的 ASCII 码值的和均为水仙花数 若分割不成功则返回 0若分割成功且分割结果不唯一 则返回-1若分割成功且分割结果唯一 则返回分割后子串的数目 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机…...
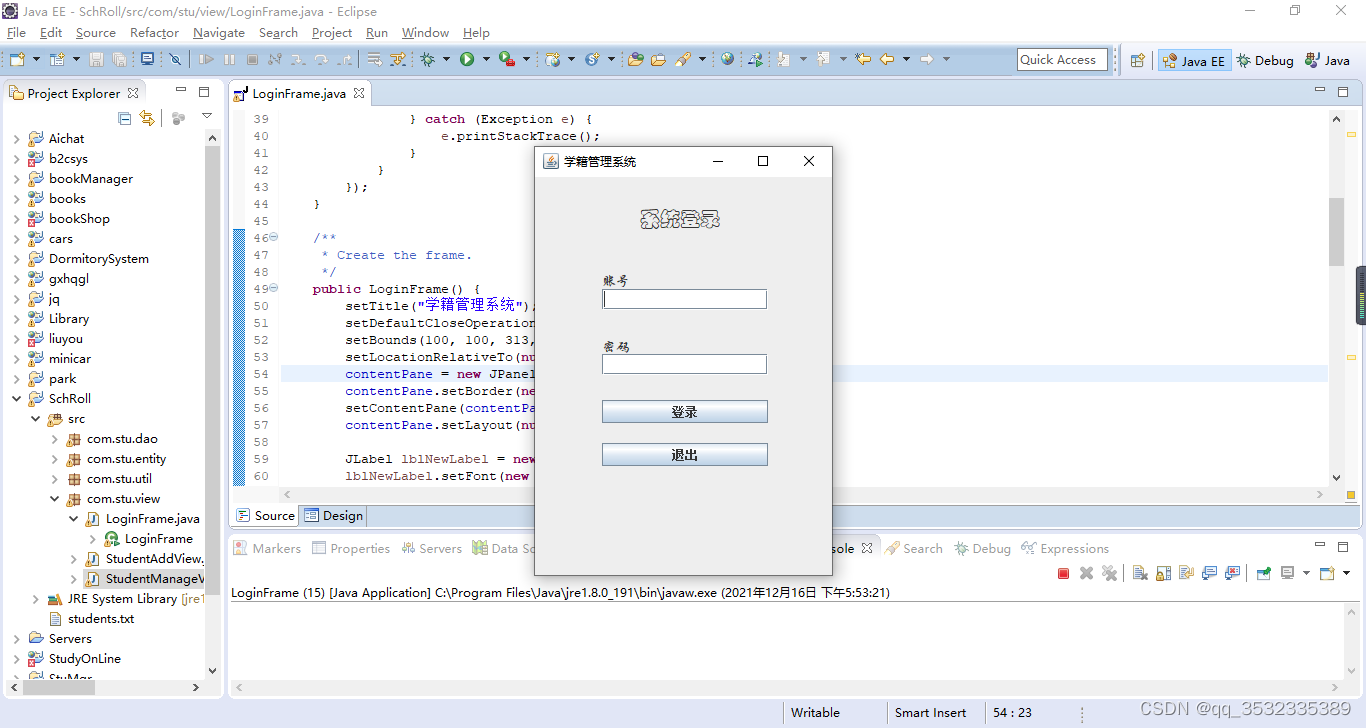
【原创】java+swing+txt学生学籍管理系统设计与实现
今天我们来介绍如何使用javaswingtxt来开发一个学籍管理系统。对的,你没看错,我们今天不用mysql,我们使用txt这个文本来进行数据存储,主要考察对文件读写的操作。 功能分析: 我们系统不要求做的很复杂,只…...
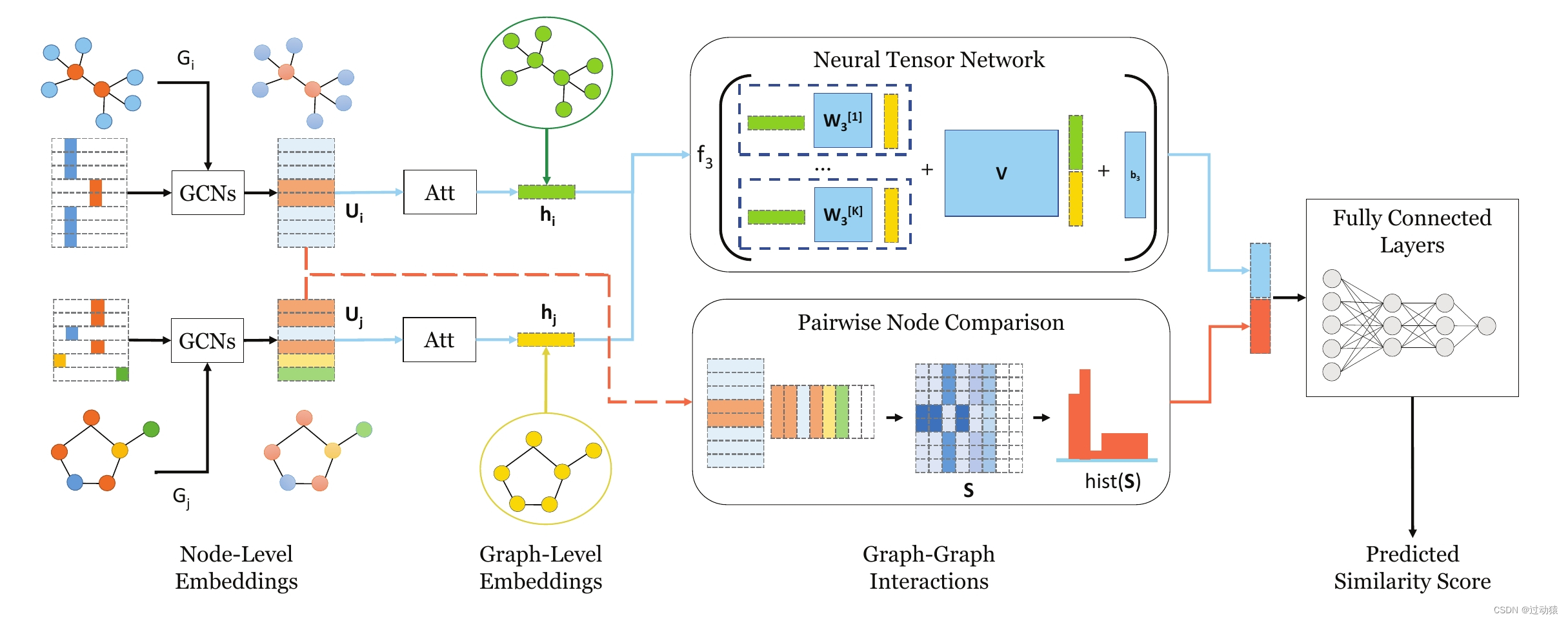
GCN项目实战1-SimGNN
文章目录SimGNN:快速图相似度计算的神经网络方法1. 数据2. 模型2.1 python文件功能介绍2.2 重要函数和类的实现SimGNN:快速图相似度计算的神经网络方法 原论文名称:SimGNN: A Neural Network Approach to Fast Graph Similarity Computation…...

经过深思熟虑后的接口测试自动化的总结与思考
序近期看到阿里云性能测试 PTS 接口测试开启免费公测,本着以和大家交流如何实现高效的接口测试为出发点,本文包含了我在接口测试领域的一些方法和心得,希望大家一起讨论和分享,内容包括但不仅限于:服务端接口测试介绍接…...
电脑自带的录屏放在哪里了?轻松弄懂,看这篇文章就明白了
有很多小伙伴有这个疑问,电脑自带的录屏放在哪里了?其实,电脑自带的录屏工具并不是所有电脑都要,具体要看你的电脑品牌和操作系统,Windows系统和Mac系统的电脑都自带了录屏工具,下面跟着小编一起来看看吧。…...
)
华为OD机试真题Java实现【字符串分割】真题+解题思路+代码(20222023)
字符串分割 给定一个非空字符串S,其被N个‘-’分隔成N+1的子串,给定正整数K,要求除第一个子串外,其余的子串每K个字符组成新的子串,并用‘-’分隔。对于新组成的每一个子串,如果它含有的小写字母比大写字母多,则将这个子串的所有大写字母转换为小写字母;反之,如果它含…...
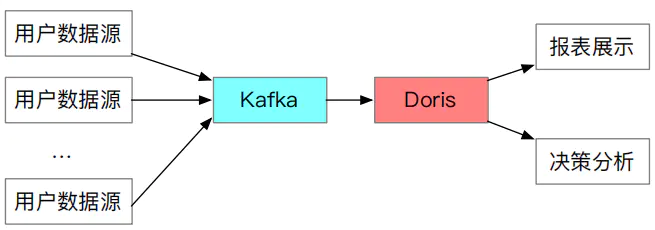
【数据库】Apache Doris : 一个开源 MPP 数据库的架构与实践
文章目录Doris 背景介绍一、Doris二、Doris 定位适用场景 & 案例介绍一、适用场景二、具体案例Doris 整体架构一、Doris 整体架构二、Doris 数据分布三、Doris 的使用方式Doris 关键技术一、数据可靠性二、易运维三、MySQL 兼容性四、支持 MPPDoris 数据模型一、Doris 数据…...

day49【代码随想录】动态规划之最长公共子序列、不相交的线、最大子序和、判断子序列
文章目录前言一、最长公共子序列(力扣1143)二、不相交的线(力扣1035)三、最大子序和(力扣53)四、判断子序列(力扣392)前言 1、最长公共子序列 2、不相交的线 3、最大子序和 4、判断…...
)
华为OD机试真题Python实现【字母消消乐】真题+解题思路+代码(20222023)
字母消消乐 题目 游戏规则: 输入一个只包含英文字母的字符串, 字符串中的两个字母如果相邻且相同,就可以消除。 在字符串上反复执行消除的动作, 直到无法继续消除为止,此时游戏结束。 输出最终得到的字符串长度。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试…...

程序中的日期使用问题-格式转化:SimpleDateFormat、org.apache.commons.lang3.time.DateUtils
前言 日期使用问题主要是格式转换的问题 场景:通过excel导入数据,其中一个字段为出生日期,需要对字段值进行合法性校验 博客地址:芒果橙的个人博客 【http://mangocheng.com】 一、个人浅谈日期 时间日期作为一个基础的标识和维度…...

C++——map和set的应用总结
目录1. 关联式容器2. 键值对3. 树形结构的关联式容器3.1 set3.1.1 set的介绍3.1.2 set的使用3.2 multiset3.2.1 multiset的介绍3.2.2 multiset的使用3.3 map3.3.1 map的介绍3.3.2 map的使用operator[]3.4 multimap3.4.1 multimap的介绍3.4.2 multimap的使用3.5 map和set在OJ中的…...

学习Python可以做什么工作?
一: 1、web开发:Python拥有非常完善与web服务器交互的库,大量的免费网页模板,相对于更具有优势,同时还具有非常优秀的Django框架,功能齐全。目前国内的豆瓣网、果壳网等,国外的Google、YouTube等…...
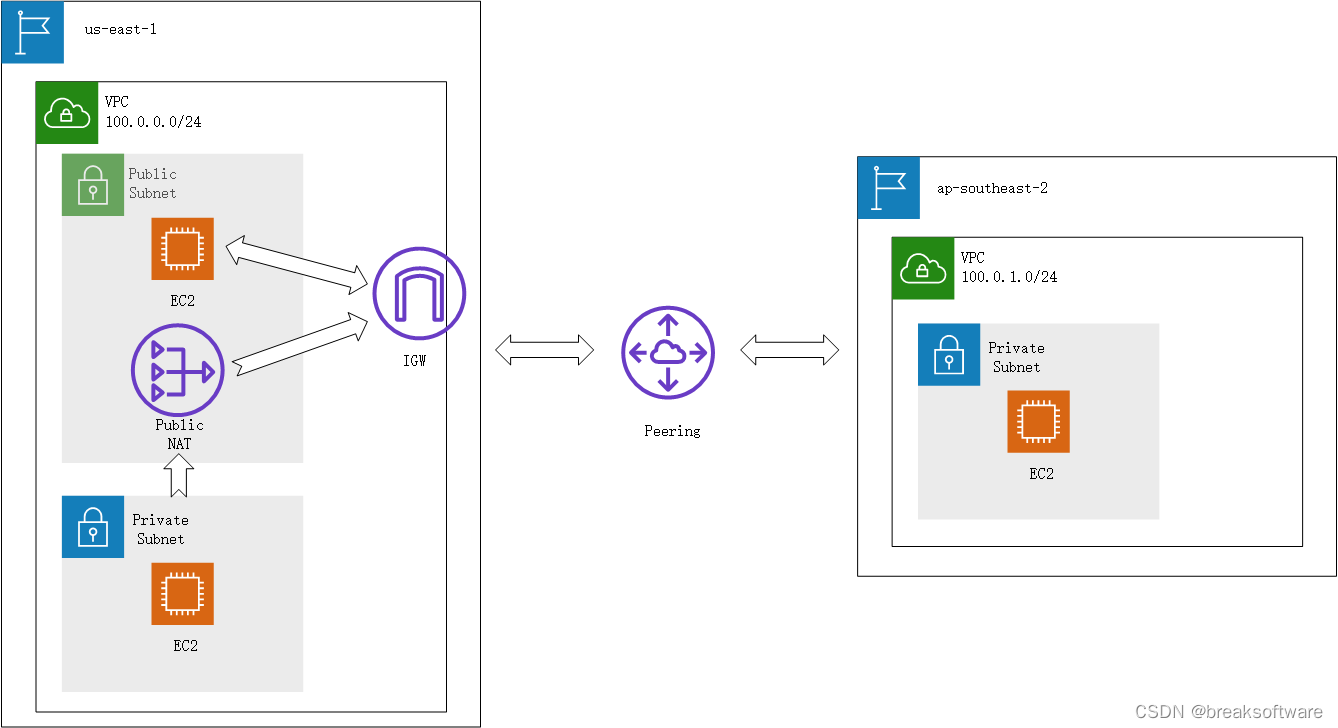
AWS攻略——Peering连接VPC
文章目录创建IP/CIDR不覆盖的VPC创建VPC创建子网创建密钥对创建EC2创建Peering接受Peering邀请修改各个VPC的路由表修改美东us-east-1 pulic subnet的路由修改悉尼ap-southeast-2路由测试知识点我们回顾下《AWS攻略——VPC初识》中的知识: 一个VPC只能设置在一个Re…...

程序员遇到人生低谷期怎么做?
每个人的一生都是起起伏伏的,你不会天天高潮,总会经历一段又一段的不如意,你怎么把握这一段段时间,如何掌控人生节奏,都源于对人生低谷期的回答。 尤其是2022年,程序员受到的冲击并不小,从年初…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
